파이썬으로 코딩 테스트 정복하기

1. sys.stdin.readline() 1) 개념 반복적으로 사용자의 입력을 받아야 하는 경우, 실행시간 단축을 위해 input() 대신 sys.stdin.readline()을 사용하는 것이 일반적이다. input 메서드를 오버라이드하는 방법은 아래와 같다. sy

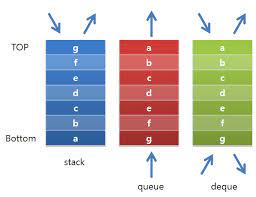
1. Stack 스택은 일반적으로 List의 append(), pop() 메서드로 구현된다.

1. Binary Search 1) 개념 이진 탐색의 특징은 아래와 같다. 리스트가 정렬되어 있다. 탐색 범위가 절반씩 줄어드는 O(logN) 알고리즘이다. 탐색 범위를 절반으로 좁히는 방법은 간단하다. 리스트의 시작점과 끝점을 start와 end로 두고, 중간지점을

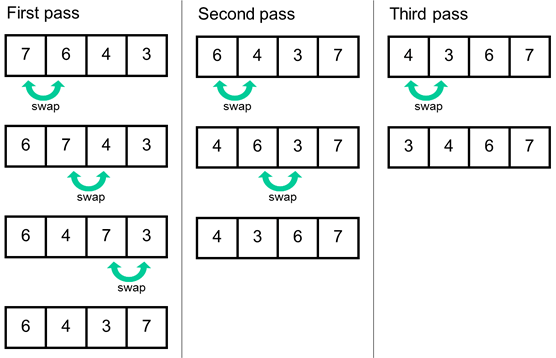
파이썬에는 이미 sort() 함수를 제공하고 있기 때문에, 사실 정렬을 직접 구현해야 하는 일은 많지 않습니다. 오히려 코딩 테스트에서는 정렬을 구현하는 방법보다도 정렬 알고리즘이 어떤 방식으로 정렬을 수행하는지를 이해하는 것이 더 중요할 수 있습니다. 따라서, 문제

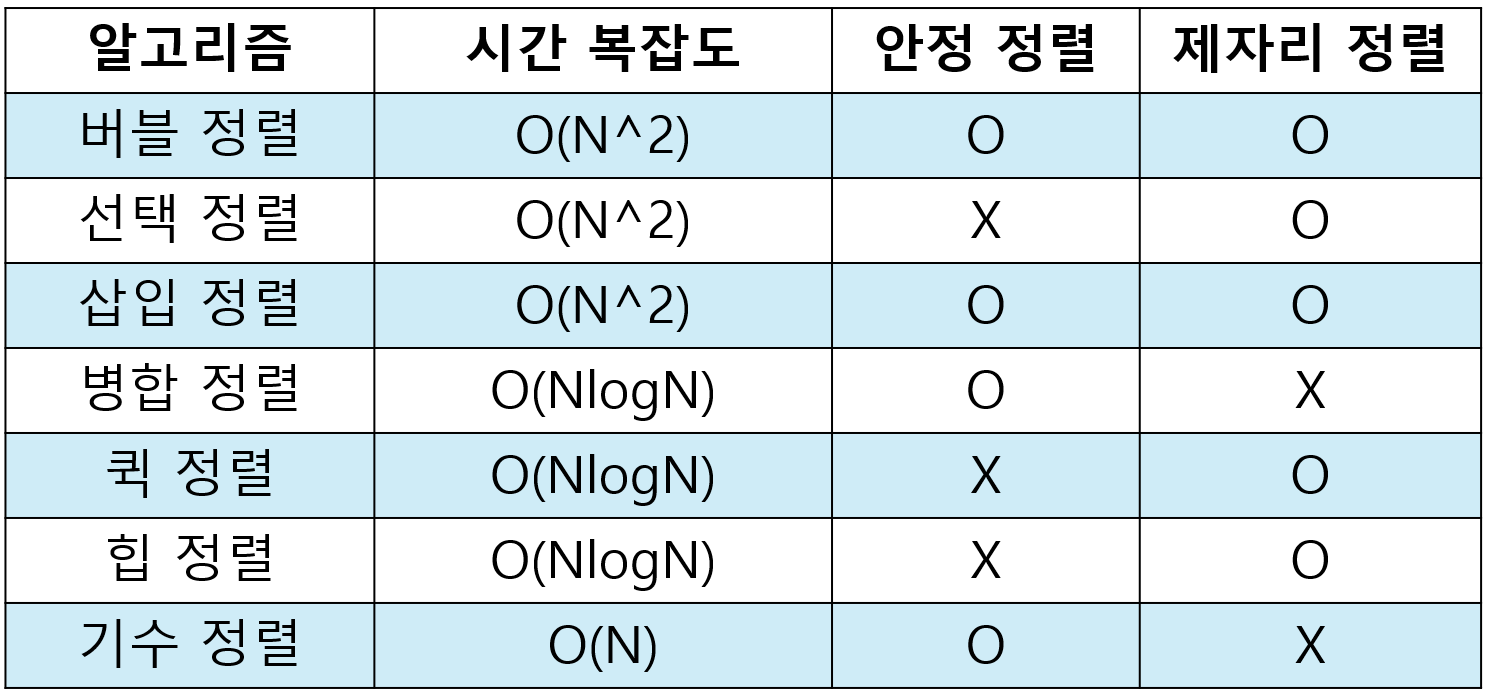
이번 시간에는 O(N^2) 정렬 알고리즘보다 조금은 복잡하지만, 더 효율적인 정렬 방법에 대해 학습해보도록 하겠습니다. 1. Merge Sort 1) 개념 병합 정렬은 Divide & Conquer 기법과 재귀 호출(반복문)을 사용하는 정렬 알고리즘이다. > ※ Di

1. 개념 그리디 알고리즘은 각 단계에서 최선의 선택을 하는 것이 최적의 선택지라고 가정하는 알고리즘이다. 각 단계에서 선택된 해가 최적해일 것이라는 보장은 없지만, 구현이 쉽고 시간 복잡도가 낮기 때문에 최적해를 구하는 일부 문제에 유용하게 사용될 수 있다. 그리디

1. 최대공약수 / 최소공배수 파이썬에서는 math 라이브러리를 import 하여 쉽게 최대공약수 및 최소공배수를 구할 수 있다. ① 최대공약수 ② 최소공배수 두 수의 곱을 최대공약수로 나누어 최소공배수를 구할 수 있다. 파이썬 3.9 버전부터는 math.lcm()

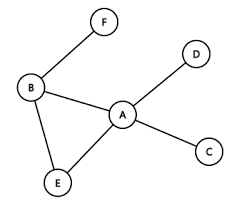
그래프 자료구조에 대해 학습하기 전, Tree 자료구조에 대한 포스팅을 먼저 참조해주시기 바랍니다. >> 자료구조 기본 - Tree 1. 그래프의 표현 Tree 자료구조를 학습할 때 배웠던 인접행렬과 인접리스트에 대해 더 자세히 알아보기로 하자. 1) 2차원 배열

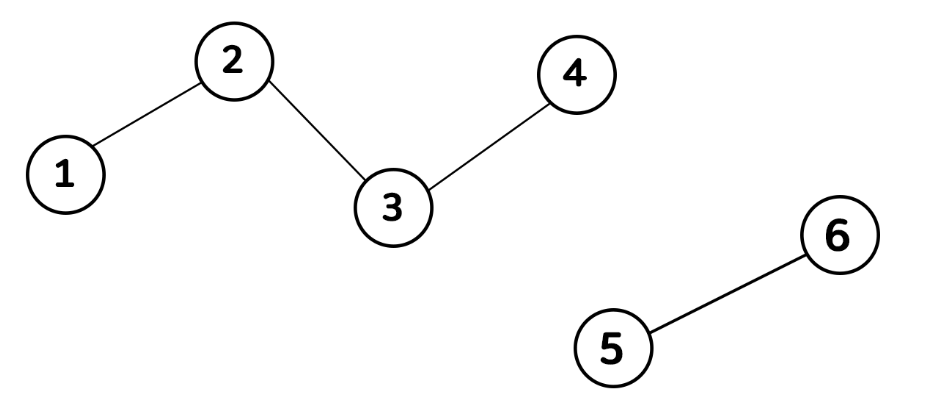
1. Union Find 1) 개념 Union Find는 Union 연산과 Find 연산으로 구성된 알고리즘을 말한다. 여기서 각 연산은 아래와 같은 의미를 가진다. Union 각 노드가 속한 집합을 합집합한다. 즉, union(A, B)는 A U B와 같다

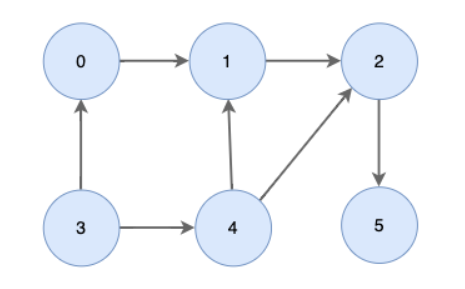
1. 위상 정렬 1) 개념 위상 정렬은 유향 그래프에서 노드 간의 순서를 결정하기 위해 사용하는 알고리즘이다. 위상 정렬의 주요 특징은 아래와 같다. 그래프 내에 사이클이 존재하지 않아야 한다. 정렬 가능한 경우의 수가 유일하지 않을 수 있다. 인접 리스트를 이용하여

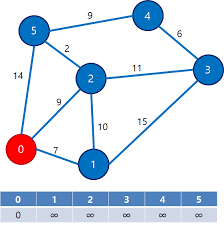
1. 다익스트라 1) 개념 다익스트라는 특정 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 알고리즘이다. 다익스트라의 특징은 아래와 같다. 모든 간선의 가중치는 0보다 크거가 같아야 한다. 시간 복잡도는 O(ElogV)가 된다. (E와 V는 각각 간선과 노드의 수

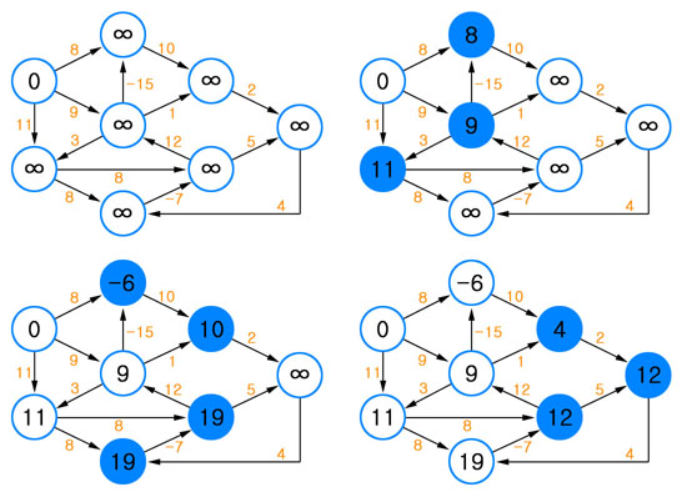
1. 벨만-포드 1) 개념 벨만-포드 알고리즘도 다익스트라 알고리즘과 마찬가지로 특정 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 알고리즘이다. 하지만, 아래와 같은 차이점이 존재한다. 가중치가 음수인 간선이 존재하는 그래프에서도 동작한다. 음수 사이클(사이클을

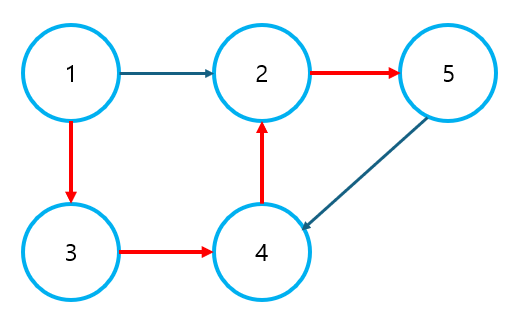
1. 플로이드-워셜 1) 개념 지난 포스팅에서 배운 다익스트라와 벨만-포드는 특정 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 One-to-Many 알고리즘이었다. 반면, 플로이드-워셜 알고리즘은 모든 노드 쌍에 대해 최단 거리를 구하는 Many-to-Many

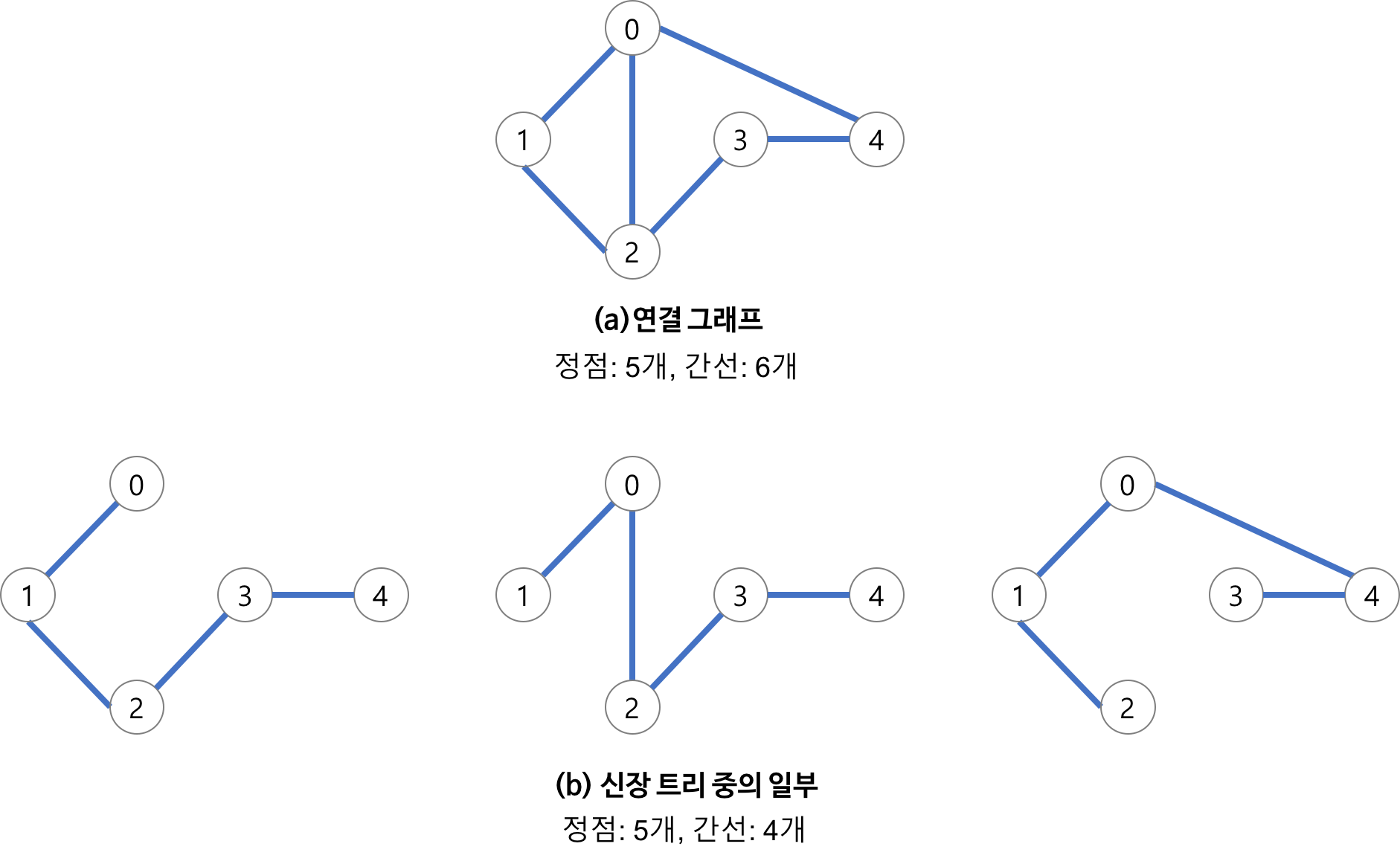
1. 최소 신장 트리 1) 개념 최소 신장 트리(Minimum Spanning Tree)에 대해 알아보기 전에, 먼저 신장 트리(Spanning Tree)가 무엇인지 알아보기로 하자. 신장 트리의 특징은 아래와 같다. 그래프의 모든 노드를 포함하는 트리를 의미하는 것으

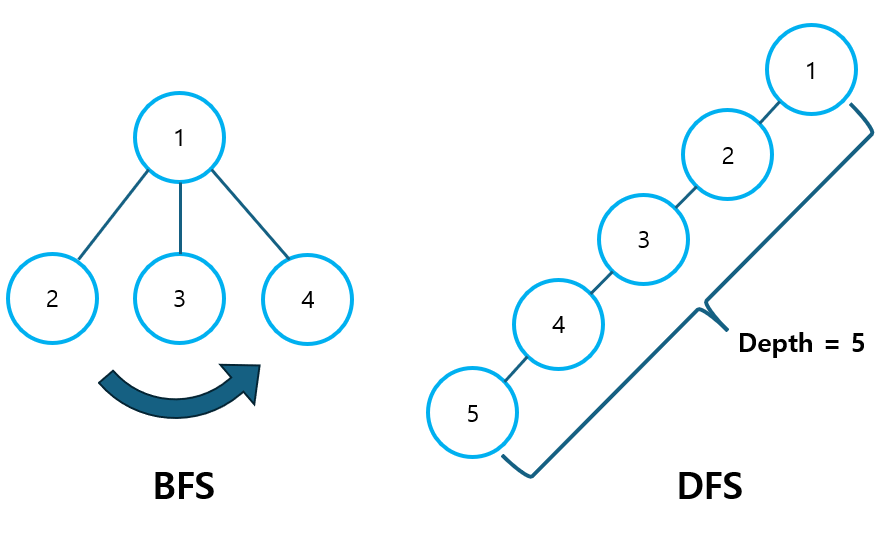
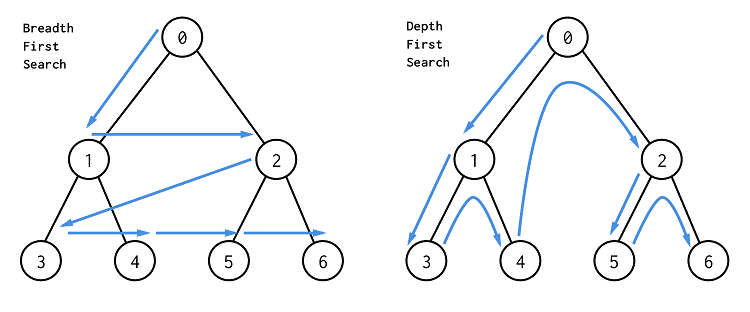
지금까지 배운 Graph의 개념을 활용하여, 이번에는 Tree 자료구조와 관련한 실전 문제를 풀어보도록 하겠습니다. 특히 이번 포스팅에서는 BFS와 DFS를 실제로 활용하는 방법에 대해 알아보겠습니다. 1. 사전 지식 1) BFS/DFS 선택 BFS/DFS 문제 중에

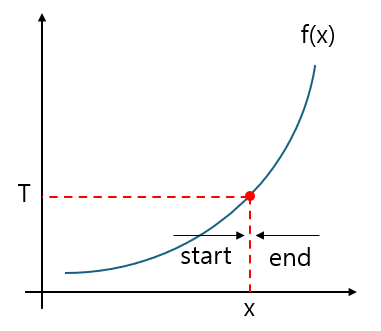
1. 블루레이 만들기 >> 백준 2343번 이진 탐색 알고리즘은 주어진 배열에서 단순히 값을 찾아내기 위한 용도 뿐 아니라, 위 문제에서처럼 가장 적절한 값을 탐색하기 위한 용도로도 자주 활용된다. 블루레이의 사이즈가 너무 크면 줄이고, 너무 작으면 늘리는 과정을 통

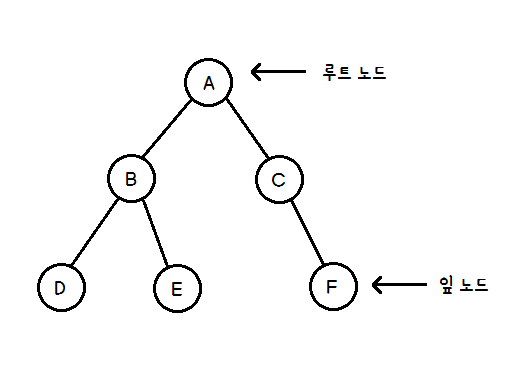
1. 트리의 부모 찾기 >> 백준 11725번 문제의 입력이 간선 형태인 것으로 보아, 인접 리스트를 이용해 트리를 표현해야 할 것이며, 노드 간의 상하 관계를 알 수 없으므로 양방향 간선으로 간주하여 풀이해야 할 것이다. 다음으로 각 노드의 부모 노드를 알아내기

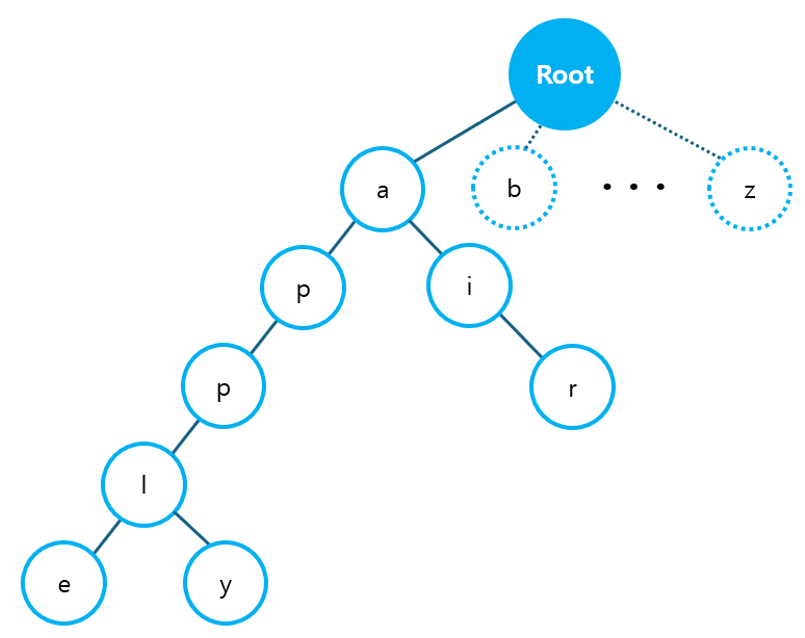
1. 문자열 검색 >> 백준 14425번 위 문제를 푸는 방법은 매우 간단하다. 집합 리스트를 src로 설정한 후 in 연산을 활용하여 몇 개의 단어가 집합 S에 포함되어 있는지 출력하면 된다. N과 M의 범위도 10^4까지이기 때문에 이중 for문을 사용해도 시간

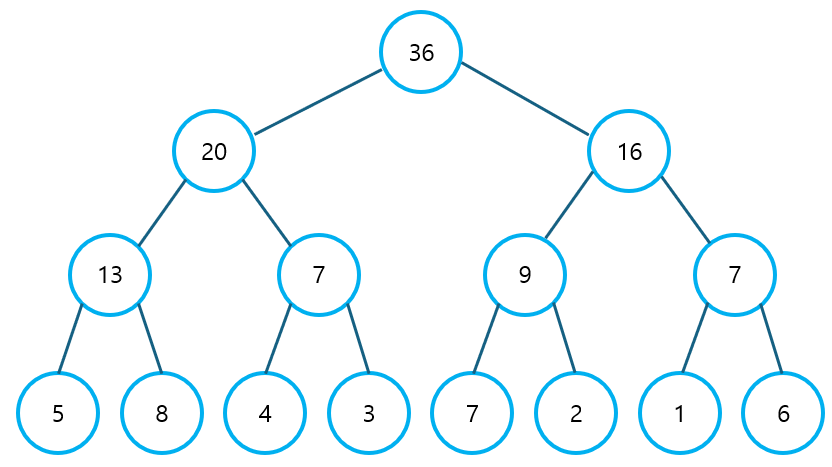
1. 세그먼트 트리 세그먼트 트리는 대규모 Data Set에서 구간 합, 최대/최소 값을 빠르게 구하기 위해 사용하는 자료구조이다. 세그먼트 트리는 아래의 3단계로 구성된다. 1) 세그먼트 트리 생성하기 ① Tree 배열 초기화 세그먼트 트리는 Full Binary

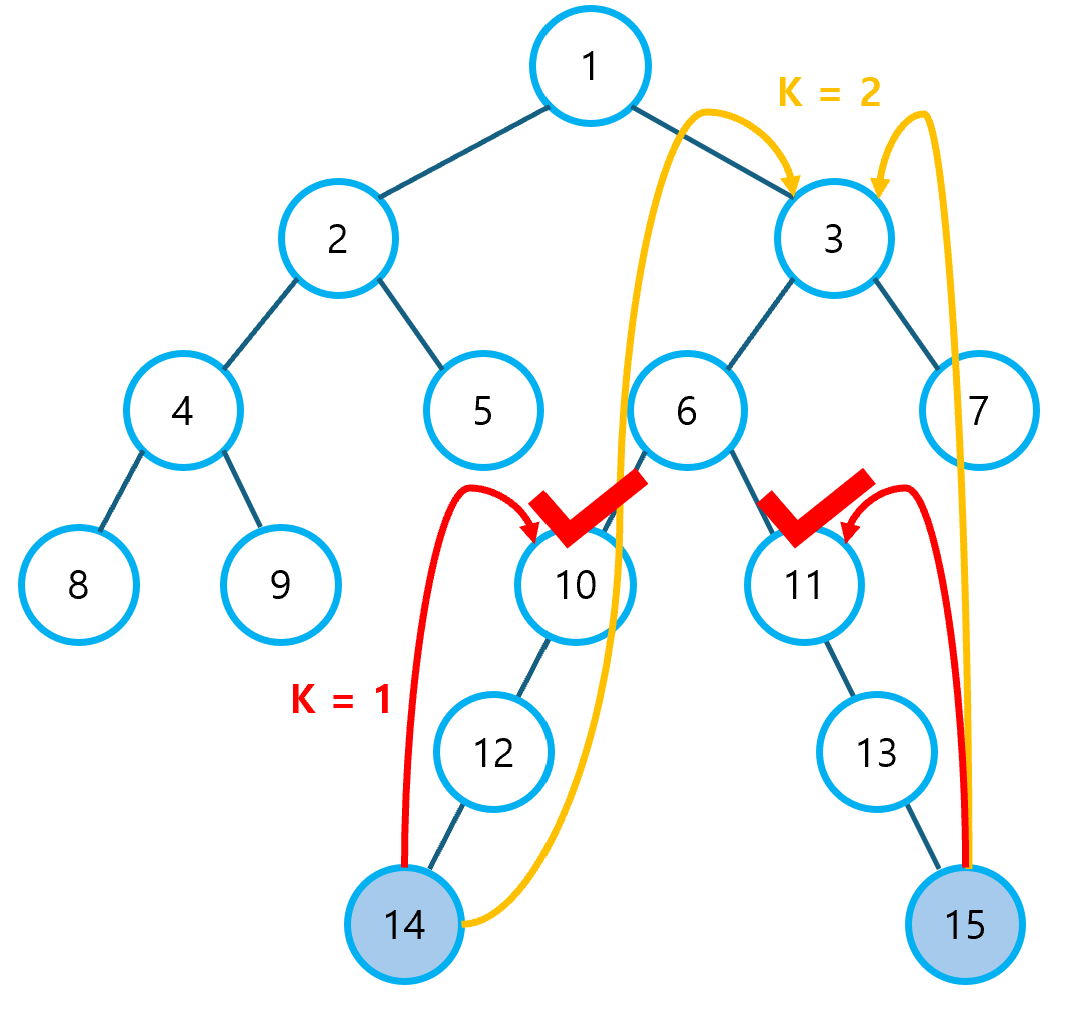
1. 최소 공통 조상 최소 공통 조상(Lowest Common Ancestor, LCA) 알고리즘은 말 그대로, 트리에서 임의의 두 노드를 선택했을 때, 두 노드의 첫 공통 부모(조상)가 되는 노드를 찾는 방법이다. 아래와 같은 트리가 있다고 하자. (참고로, 꼭 이진

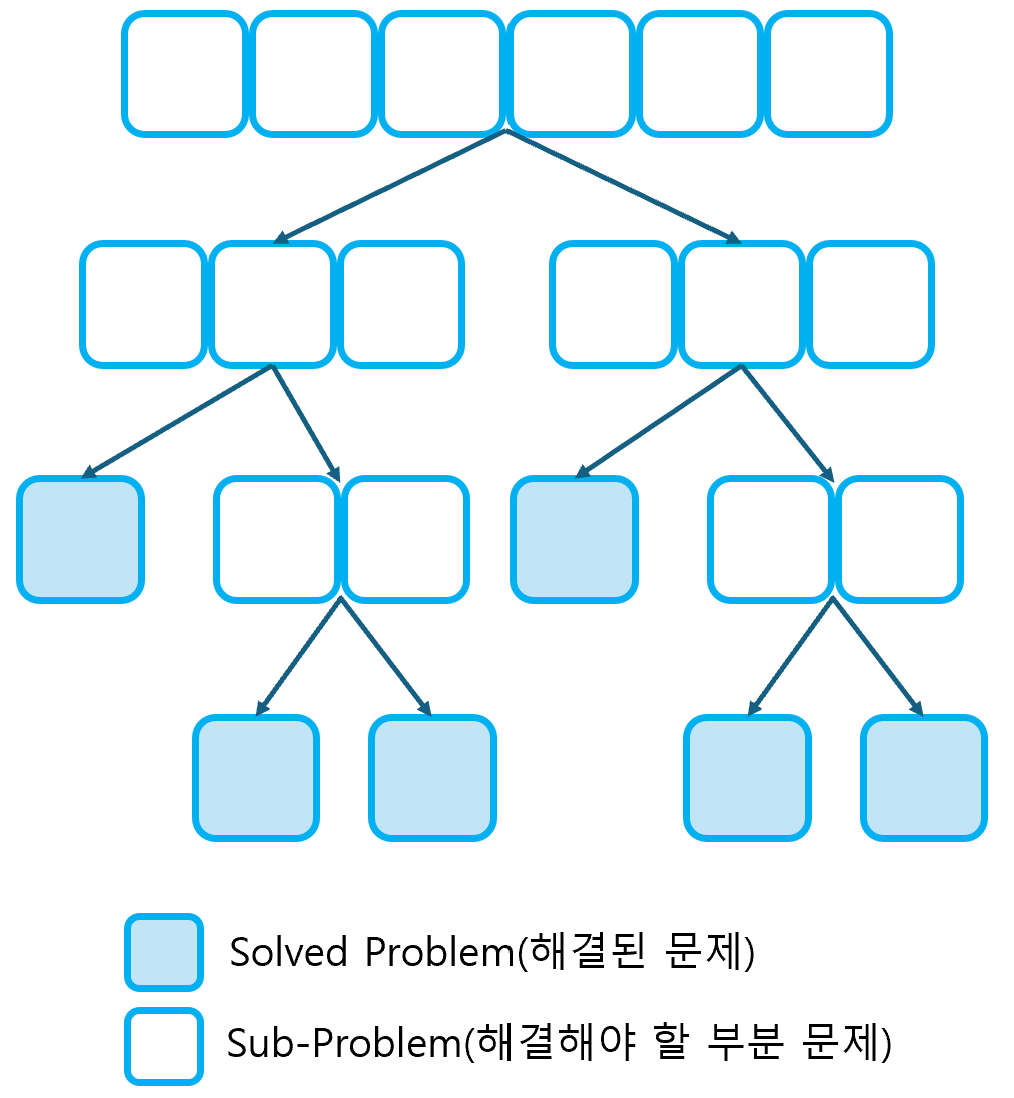
1. 색종이 만들기 >> 백준 2630번 분할 정복은 큰 문제를 작은 문제로 분할하여 해결한 후, 해결 결과를 차례로 병합해나가며 전체 문제의 해답을 알아내는 설계 전략이다. 분할 정복법의 자세한 개념은 문제를 풀어보면서 이해해보기로 하자. 2. Z 방향으로 탐색하

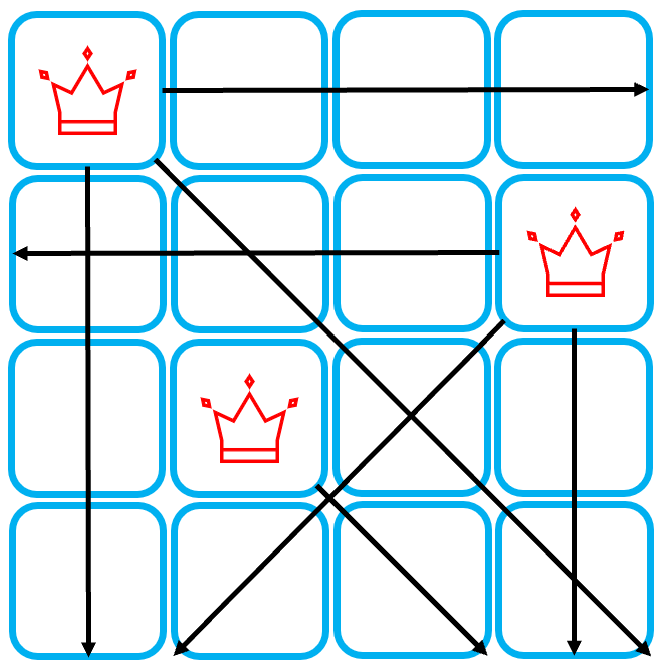
1. 백트래킹 1) 개념 백트래킹이란, 가능한 모든 해를 탐색하되, 조건에 맞지 않는 경우 탐색을 중단함으로써, 효율적으로 해를 찾는 알고리즘을 말한다. 백트래킹의 의미를 한 마디로 정의하면 아래와 같다. > Go as deeply as possible, Backtr

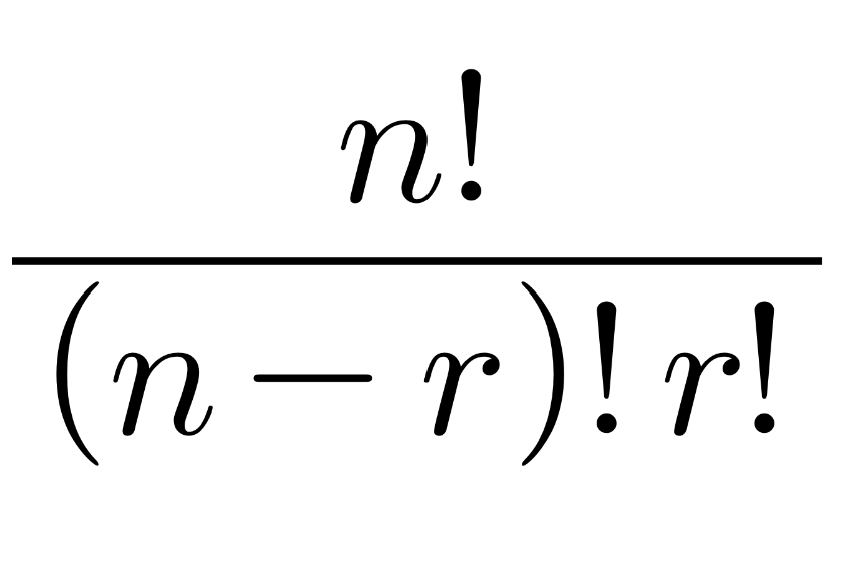
조합은 n개의 원소 중 r개를 선택하는 경우의 수를 의미하며, 수학적 공식으로는 아래와 같이 나타낸다.조합의 개념은 그 자체로도 매우 중요하지만, 무엇보다도 나중에 배울 동적 계획법의 기초가 되는 내용이기 때문에 반드시 이해하고 넘어가야 한다.조합의 개념이 동적 계획법

1. 다리 놓기 >> 백준 1010번 다리끼리 서로 겹쳐지지 않는다는 조건이 있기 때문에 위 문제는 M개의 사이트 중 N개를 선택하는 문제로 해석할 수 있다. 입력 값의 범위가 크지 않기 때문에 직접 조합을 계산하여 풀이해도 무방할 것으로 보인다. ① math 라이

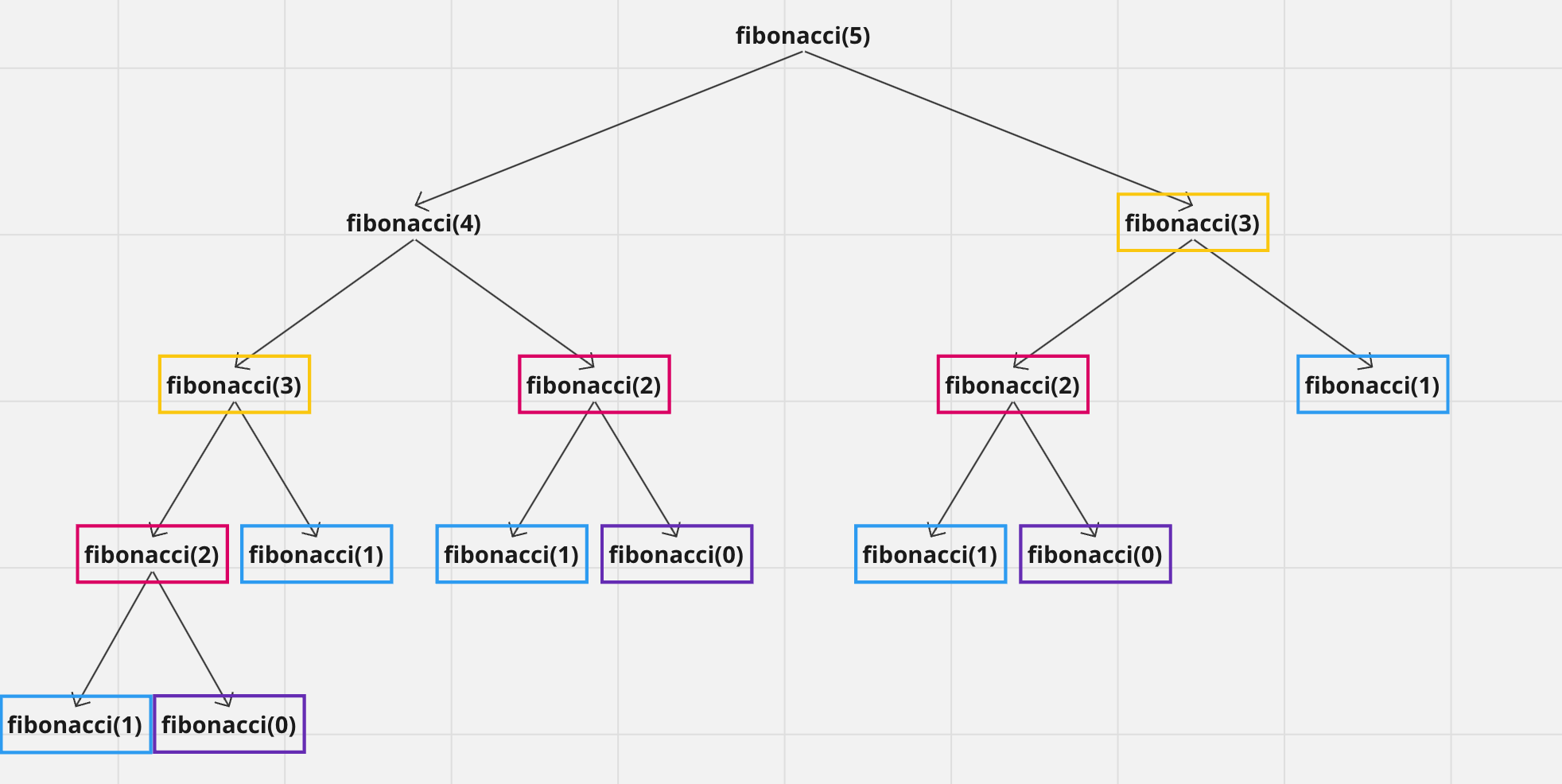
1. 동적 계획법 1) 개념 동적 계획법은 복잡한 문제를 간단한 하위 문제로 나눈 후, 하위 문제를 해결함으로써 최종적으로 복잡한 문제의 해답을 구하는 알고리즘 설계 기법이다. 동적 계획법은 중복된 계산을 제거함으로써 시간 복잡도를 낮출 수 있다는 장점이 있지만, 부분

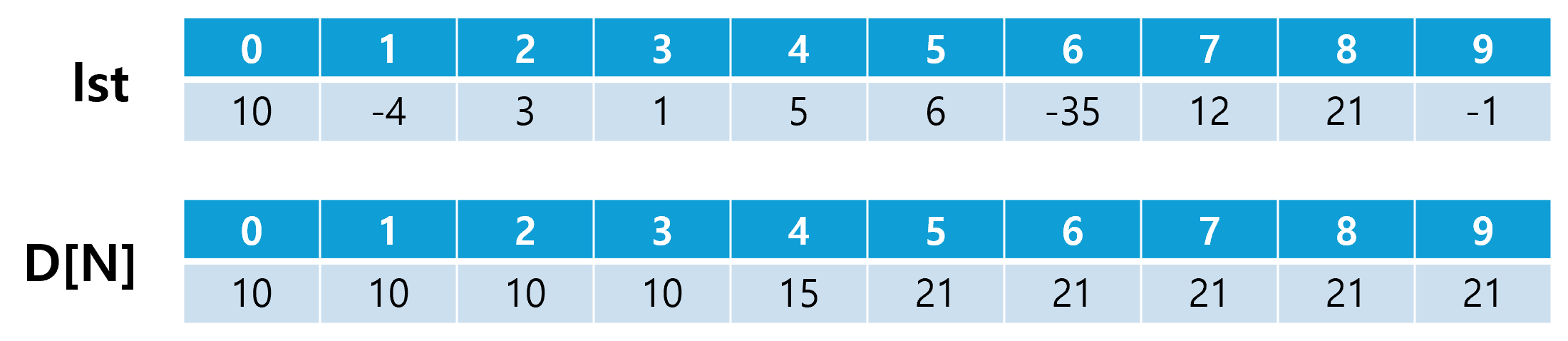
1. 이친수 구하기 >> 백준 2193번 1) 일반적인 풀이 1이 두 번 연속으로 나타나지 않는다는 조건에서 DP를 연상할 수 있어야 한다. 그 이유는 (N-1) 자리 이친수 중 0으로 끝나는 수의 개수와 1로 끝나는 수의 개수를 알고 있다면, 그 숫자 뒤에 0 또는

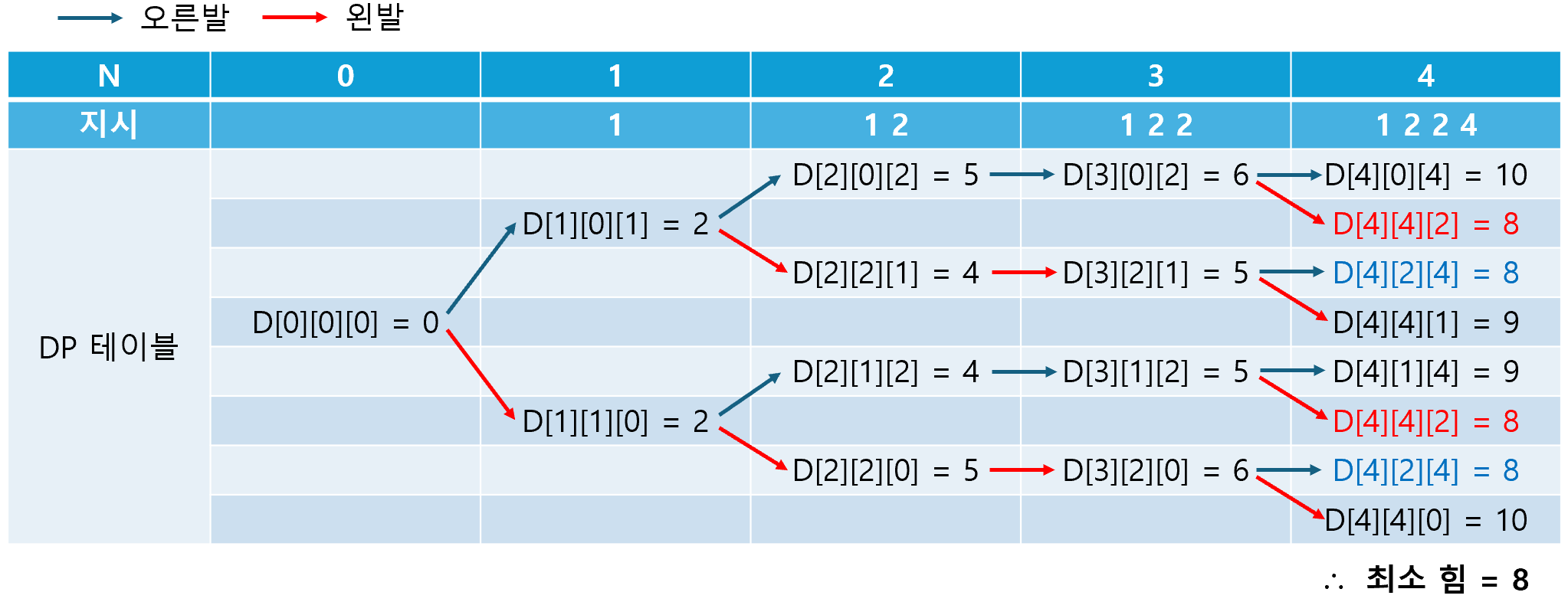
1. 최장 공통 부분 수열 찾기 >> 백준 9252번 여기서 말하는 부분 수열이란, 원래의 수열에서 순서를 유지하면서 만들어낼 수 있는 수열을 말한다. 예를 들어, 원래의 수열이 [A,B,C,D,E]일 때, 만들 수 있는 부분 수열에는 [A,B,C], [B,D,E],

1. 행렬 곱 연산 횟수의 최솟값 구하기 >> 백준 11049번 연쇄 행렬 곱셈(Matrix Chain Multiplication) 문제도 대표적인 DP 문제이다. 이 문제의 점화식을 도출하기 위해서는 행렬 곱의 두 가지 성질을 이해해야 한다. ① N개의 행렬 곱을

1. CCW 기하 관련 문제를 풀이할 때, 필수적으로 알아두어야 하는 알고리즘으로 CCW(Counter-Clockwise)가 있다. 여기서 CCW란, 벡터의 외적을 이용하여 3개의 점에 대한 위치 관계를 판단하는 알고리즘이다. 아래와 같이 3개의 점이 주어졌을 때,

Ⅰ. 자료구조 기본 1. Stack, Queue, Deque Stack, Queue, Deque는 말 그대로 기본 자료구조인만큼 리뷰할만한 내용이 거의 없다. 아래의 두 가지 내용만 잘 알아두고 있어도 충분한 것 같다. ① Deque의 import 문 ② Deque

Ⅴ. Graph 1. 그래프의 표현 ① 그래프 표현 문제의 입력이 행렬 형태이거나, 트리 순회를 구현하는 경우가 아니라면, 모두 인접 리스트를 이용하여 그래프를 표현한다. 무향 그래프의 경우 양방향 간선을 고려한다. ② 그래프 순회 그래프 순회에는 BFS/DFS가 사

4. 다익스트라 ① 정의 특정 노드로부터 다른 모드까지의 최단 거리를 구하는 One-to-Many 알고리즘이다. ② 특징 모든 간선의 가중치는 0보다 크거나 같아야 한다. 유향 그래프, 무향 그래프, 사이클을 포함하는 그래프에서 모두 사용할 수 있다. ③ 구현에 사

Ⅵ. Tree 1. BFS/DFS 1) BFS/DFS 선택 ① 노드 탐색의 방향성이 명확하게 상하 또는 좌우인 경우에 대해서는 각각 DFS와 BFS를 사용하면 된다. ② 탐색 방향이 명확하지 않은 경우, 아래의 기준을 적용한다. 인접한 노드를 탐색해야 하는 문제 →

4. 트라이 1) In 연산 In 연산의 시간 복잡도는 List나 Tuple에서 O(N), Set이나 Dictionary에서 O(1)이다. Set 자료구조에서는 add와 remove 메서드를 통해 원소를 삽입 및 삭제할 수 있다. 2) 트라이 ① Node 클래스 ②

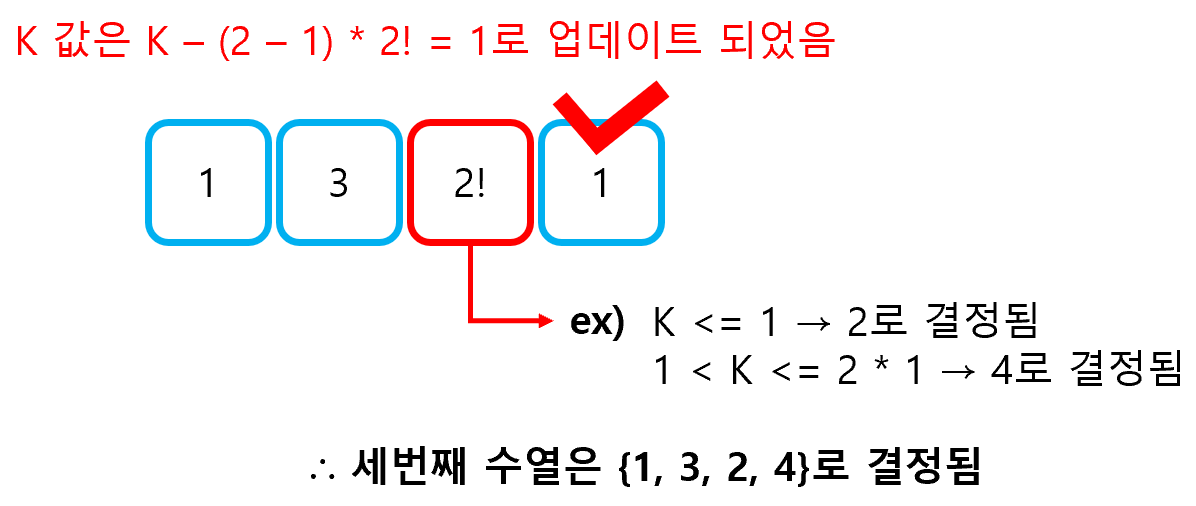
Ⅶ. 조합 ① 조합 계산 방법 ② DP 테이블 초기화 및 업데이트 ③ 완전 순열의 DP 테이블 DP 테이블의 Size를 입력 값으로 설정할 경우, 입력 값이 1일 때 D[2] = 1에서 IndexError가 발생한다. 따라서, DP 테이블을 고정 크기로 생성할 것을

1. Utilty 관련 메서드 간혹 낮은 난이도의 문제에서 유틸리티 관련 메서드에 대해 물어보는 경우가 있기 때문에, 이러한 메서드도 미리 알아두면 쉬운 문제를 빠르게 푸는 데에 도움이 될 것이다. 1) 오늘의 날짜 또는 시간 출력하기 > ※ 관련 문제 >> 백준