1. 최소 신장 트리
1) 개념
최소 신장 트리(Minimum Spanning Tree)에 대해 알아보기 전에, 먼저 신장 트리(Spanning Tree)가 무엇인지 알아보기로 하자. 신장 트리의 특징은 아래와 같다.
- 그래프의 모든 노드를 포함하는 트리를 의미하는 것으로, 하나의 그래프 내에 여러 개의 신장 트리가 존재할 수 있다.
- N개의 노드를 N-1개의 간선 즉, 사이클 없이 최소 간선만으로 모든 노드를 연결한다.
- 음수 간선 가중치를 허용한다.
위 조건을 만족하는 그래프는 반드시 계층 구조를 갖게 되므로, 이를 신장 트리라고 부르는 것이다.
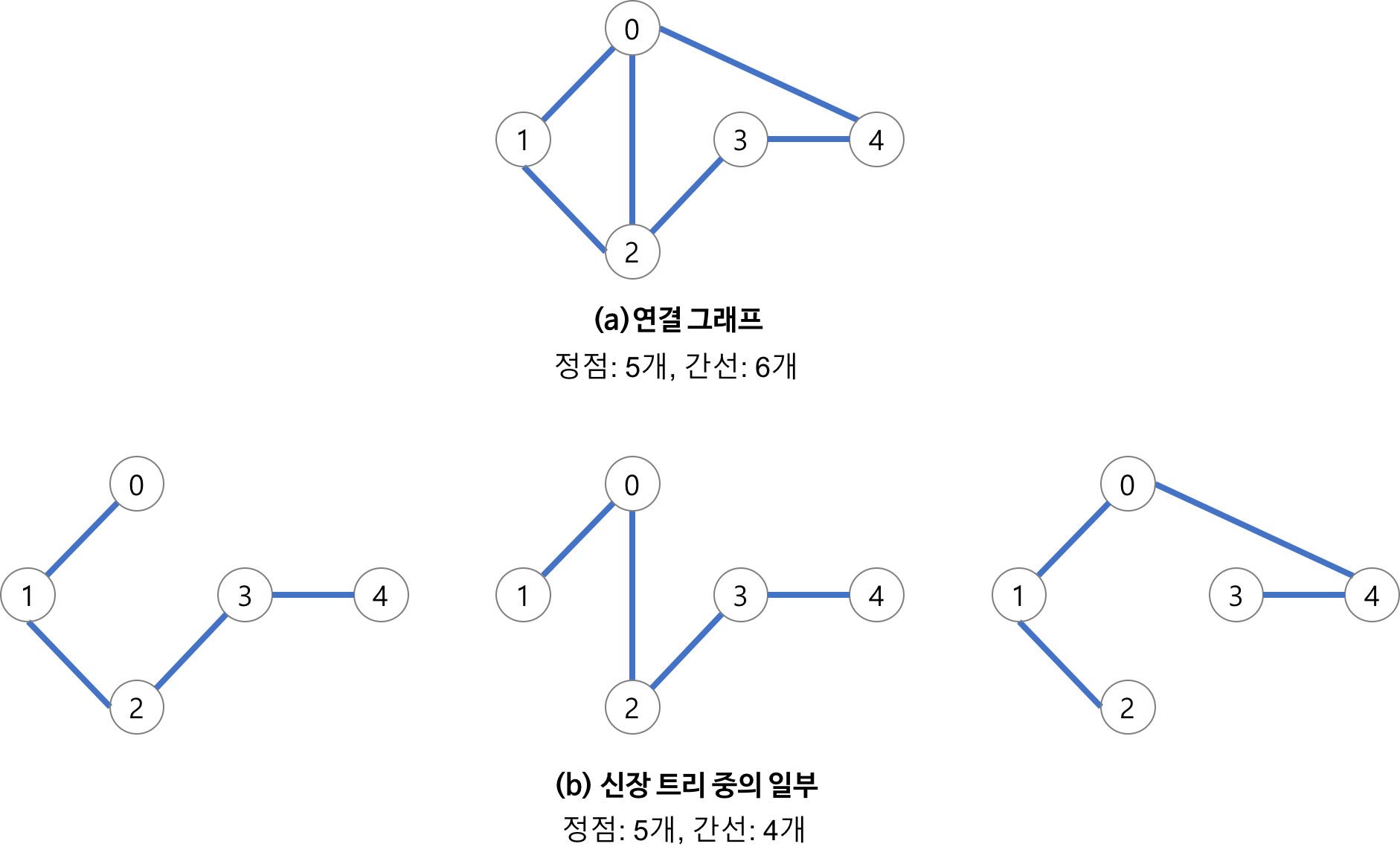
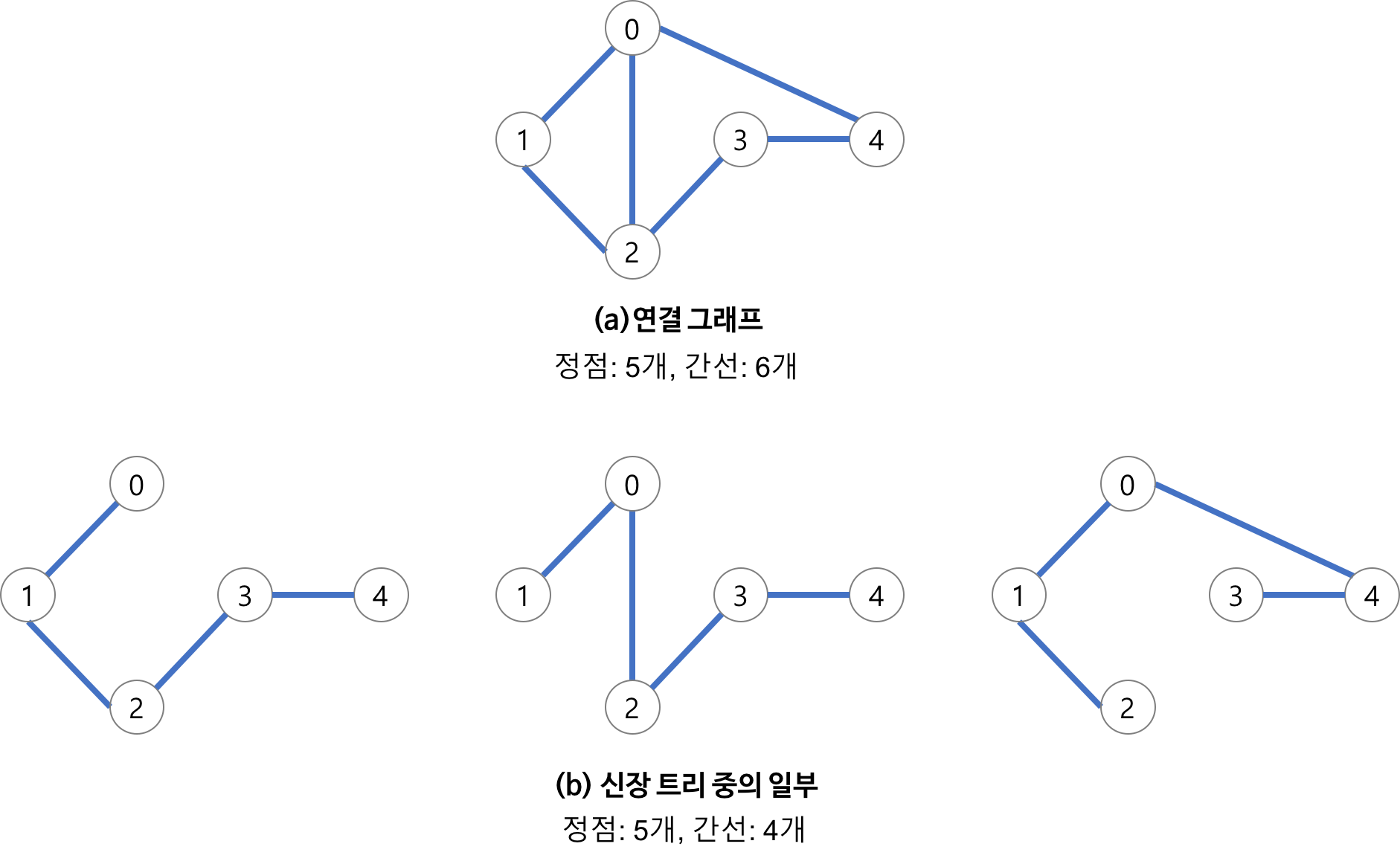
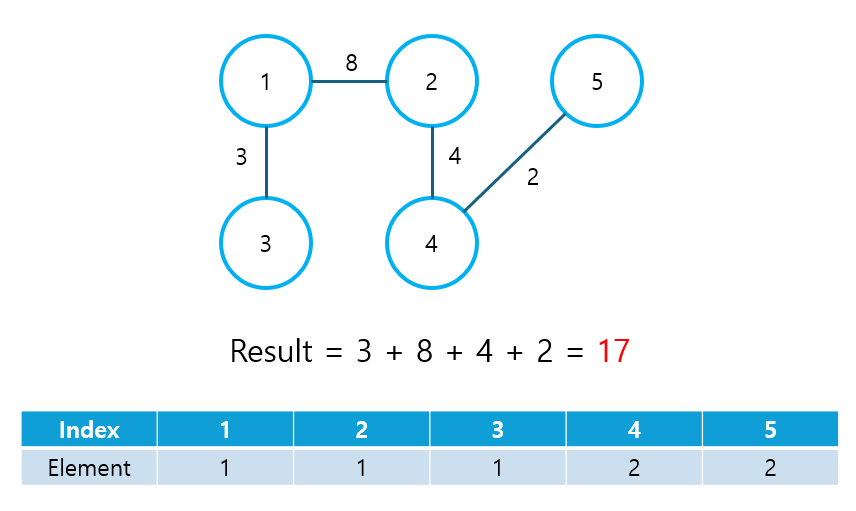
위 그림에서처럼 신장 트리는 가능한 여러 가지의 조합이 존재하는데, 그중에서도 간선 가중치의 합이 최소가 되는 신장 트리를 최소 신장 트리라고 한다. 최소 신장 트리를 찾아내는 알고리즘에는 간선 선택 기반의 Kruskal 알고리즘과 노드 선택 기반의 Prim 알고리즘이 있는데, 여기서는 Kruskal 알고리즘의 동작 원리만 알아보기로 한다.
※ Kruskal 알고리즘만 알아보는 이유
이론적으로는 간선 수가 적은 그래프의 경우, 시간 복잡도가 간선 수에 비례하는 Kruskal 알고리즘이 유리하고, 간선 수가 많은 그래프의 경우, 시간 복잡도가 노드 수에 비례하는 Prim 알고리즘이 유리하다.
그러나 Prim 알고리즘으로 풀이할 수 있는 모든 문제는 Kruskal 알고리즘으로 대체하여 풀이할 수 있고, Kruskal 알고리즘의 구현과 메커니즘이 더 간단하기 때문에, 적어도 코딩 테스트에서는 Kruskal 알고리즘만 알고 있어도 충분하다.
2) Kruskal 알고리즘
Kruskal 알고리즘은 최소 가중치의 간선을 Greedy 하게 선택해나가는 방식으로, 최소 신장 트리를 구성한다. 이 때, 사이클 형성 여부를 확인하기 위해 Union Find 알고리즘이 사용된다. 자세한 동작 원리는 아래와 같다.
① Edge List와 Union Find List를 초기화한다.
- Kruskal 알고리즘은 간선 중심 알고리즘이므로, 그래프를 간선 리스트로 표현해야 한다.
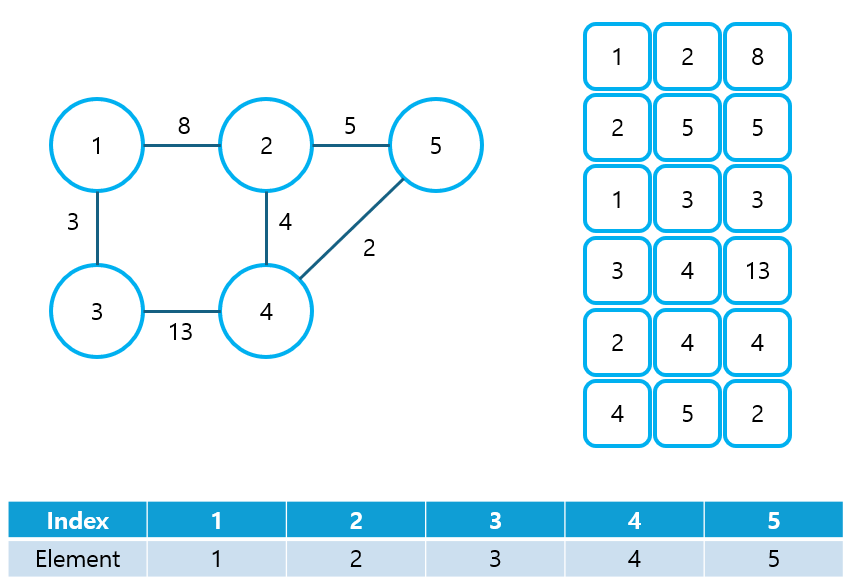
② 가중치를 기준으로 간선들을 오름차순 정렬한다.
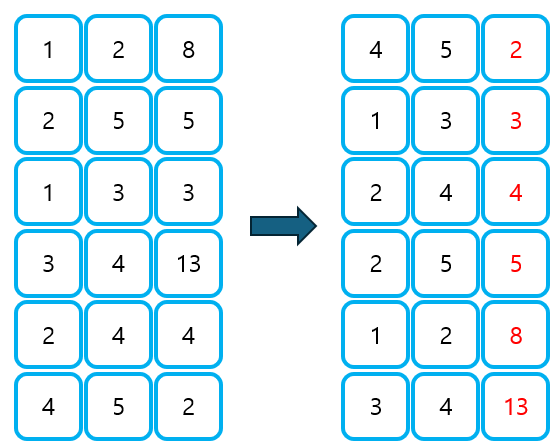
③ 정렬된 순서대로 간선을 선택하되, 사이클이 형성되지 않아야 한다.
- find 연산을 이용해 각 노드의 대표 노드가 동일한지 확인한다. 두 노드의 대표 노드가 동일할 때, 두 노드를 연결하면 사이클이 형성된다.
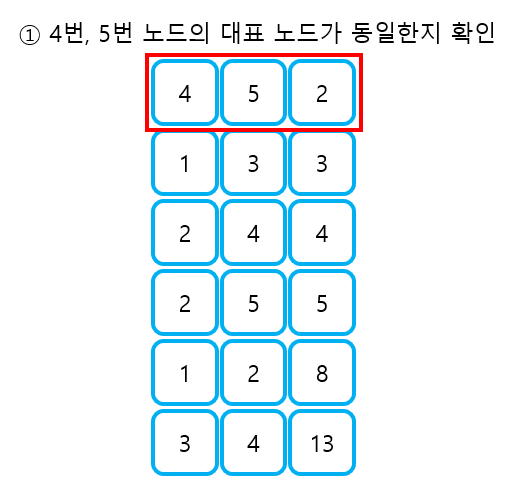
- 두 노드의 대표 노드가 다른 경우에만, union 연산을 이용해 노드를 연결한다.
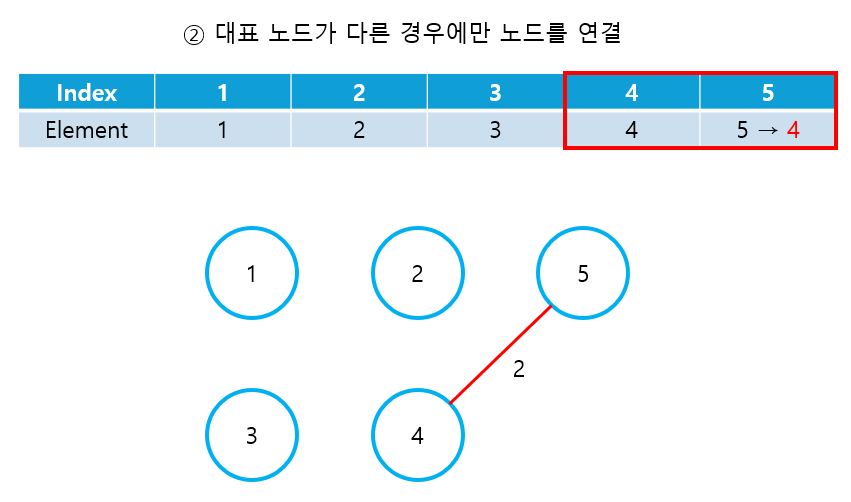
④ 이 과정을 총 (N-1)번 반복하면서, 그 때마다 선택된 간선의 가중치를 더해나간다. 반복이 끝났을 때, 가중치의 총합이 곧 최소 신장 트리의 가중치가 된다.
2. 문제 풀이
1) 최소 신장 트리 구하기
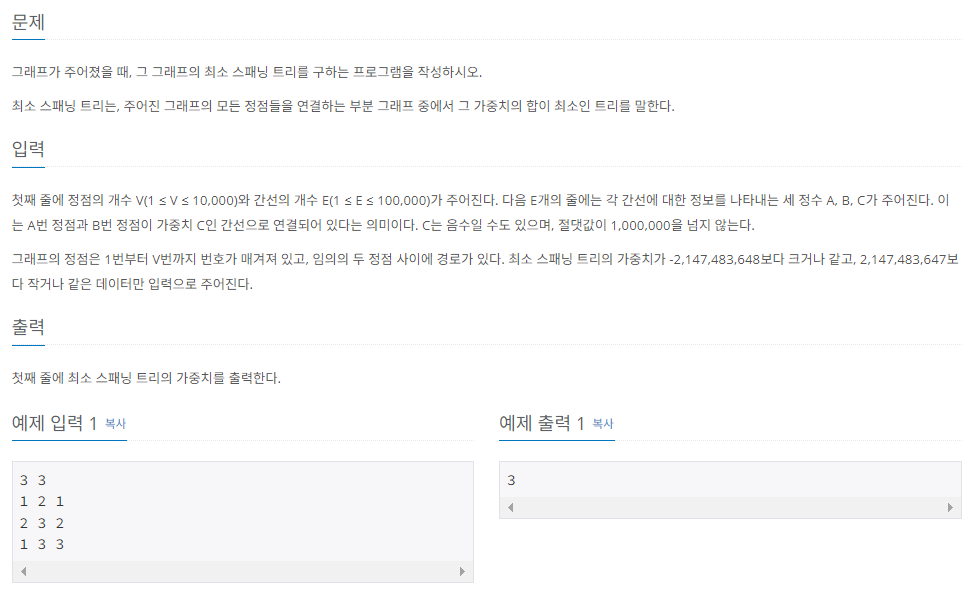
지금까지 배운 내용을 토대로 위 문제를 풀이해보자.
import sys
from queue import PriorityQueue
input = sys.stdin.readline
V, E = map(int, input().split())
# Union Find 리스트
lst = [x for x in range(V + 1)]
# 가중치 기준 정렬을 위한 우선 순위 큐
pq = PriorityQueue()
for i in range(E):
u, v, w = map(int, input().split())
pq.put((w, u, v)) # 튜플의 맨 앞의 값을 기준으로 정렬하므로, 가중치를 맨 앞에 위치시켜 put
def find(a):
if a == lst[a]:
return a
lst[a] = find(lst[a])
return lst[a]
def isSameSet(a, b):
a = find(a)
b = find(b)
return a == b
def union(a, b):
a = find(a)
b = find(b)
lst[b] = a
edgeCnt = 0 # 간선 사용 횟수
result = 0 # 최소 신장 트리의 가중치
while edgeCnt < (V - 1):
w, u, v = pq.get()
if not isSameSet(u, v):
union(u, v)
edgeCnt += 1
result += w
print(result)위 코드 중 아래의 내용을 주의 깊게 살펴보기 바란다.
① Priority Queue
- 가중치 기준 오름차순 정렬을 위해 우선순위 큐를 사용하였다.
- 직접 정렬을 수행하는 것보다 코드가 간결해지는 효과가 있다.
② Union Find
- 기존에 사용하던 Union Find 알고리즘을 그대로 사용하였다.
- Union Find 알고리즘의 기본 틀은 암기해 둘 것을 권장한다.
③ while 문
- 사이클 형성으로 인해 union 되지 않는 경우가 존재하므로, for 문을 (N - 1)번 반복하는 방식은 사용할 수 없다.
- while 문의 반복 횟수는 헷갈리는 경우가 많으므로, 본인만의 규칙을 만들어 두는 것이 좋다. 아래의 규칙 중 하나를 선택하여 사용할 수 있다.
- 반복 변수는 0으로 초기화하고, 등호 없는 부등호로 대소를 비교한다.
- 반복 변수는 1로 초기화하고, 등호 있는 부등호로 대소를 비교한다.
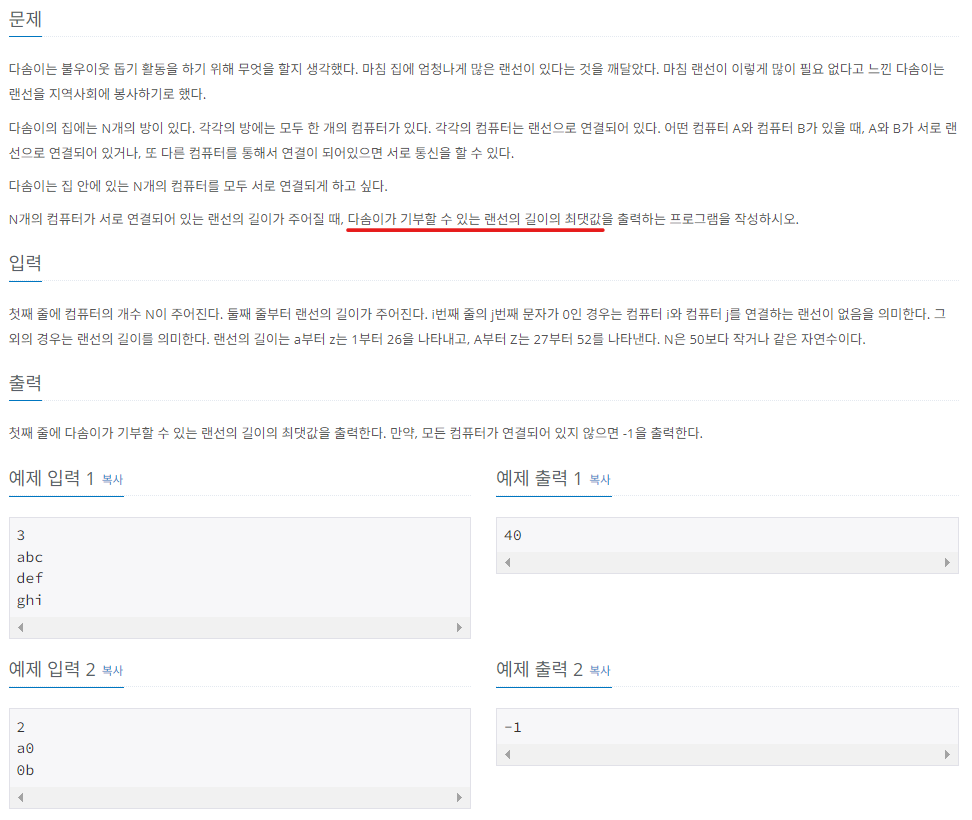
2) 불우이웃 돕기
위 문제를 요약하면, N개의 컴퓨터를 (N-1)개의 랜선으로 연결하면서 연결된 랜선 길이의 합이 최소가 되어야 한다는 것이다. 따라서, 위 문제는 최소 신장 트리를 이용해 풀이해야 하는 문제이다.
Kruskal 알고리즘을 사용하기 위해선 간선 리스트를 이용해 그래프를 표현해야 하는데, 문제에서는 인접 행렬 형태로 그래프를 표현하고 있다. 따라서, 인접 행렬을 통해 간선 정보를 추출하는 작업이 필요할 것이다. 다만, 인접 행렬에서 i와 j가 같은 곳의 랜선 길이는, 모든 컴퓨터를 최소 연결하는데에 필요하지 않으므로 무시하도록 하겠다.
마지막으로, 알파벳을 숫자로 변환하기 위해 파이썬의 내장 함수인 ord() 메서드를 사용할 것이다. ord() 메서드는 주어진 문자의 Uni Code 또는 ASCII Code를 반환하는 역할을 수행한다. 위 내용을 적용하여 문제를 풀어보자.
import sys
from queue import PriorityQueue
input = sys.stdin.readline
N = int(input())
pq = PriorityQueue()
total = 0 # 기부할 랜선의 길이
for i in range(N):
temp = list(input()) # [a, b, c]
for j in range(N):
if 'a' <= temp[j] <= 'z':
w = ord(temp[j]) - ord('a') + 1
elif 'A' <= temp[j] <= 'Z':
w = ord(temp[j]) - ord('A') + 27
else: # temp[j]가 0인 경우
w = 0
total += w # 일단 랜선의 총 길이를 구한 후, 나중에 최소 신장 트리의 가중치만큼 뺄 예정
if i != j and w != 0: # i와 j가 같은 곳의 랜선이 아니면서, 연결된 간선인 경우
pq.put((w, i, j)) # 간선 리스트 생성 없이 바로 PQ에 저장
# Union Find 리스트
lst = [x for x in range(N)]
def find(a):
if a == lst[a]:
return a
lst[a] = find(lst[a])
return lst[a]
def isSameSet(a, b):
a = find(a)
b = find(b)
return a == b
def union(a, b):
a = find(a)
b = find(b)
lst[b] = a
edgeCnt = 0 # 간선 사용 횟수
result = 0 # 최소 신장 트리의 가중치
# 모든 간선을 사용했음에도, 모든 컴퓨터가 연결되지 않는 경우를 고려
while pq.qsize() > 0:
w, u, v = pq.get()
if not isSameSet(u, v):
union(u, v)
edgeCnt += 1
result += w
if edgeCnt == (N - 1):
print(total - result)
else:
print(-1)주의할 점은 1번 문제에서 사용했던 while edgeCnt < (N - 1) 로직을 그대로 사용하지 않고, while pq.qsize() > 0을 사용했다는 것이다. 그 이유는 위 문제는 1번 문제와 달리 신장 트리가 만들어지지 않는 경우도 존재하기 때문이다.
신장 트리가 만들어지지 않는 경우, (N - 1)개의 간선을 사이클 형성 없이 연결할 수 없다. 그러므로, 신장 트리를 만들 수 없는 그래프에 while edgeCnt < (N - 1) 로직을 적용하면, 무한 루프가 발생하게 된다. 그 이유는 모든 간선이 PQ에서 get() 되어 empty 상태가 된 PQ에, get() 메서드를 호출할 경우, PQ에 새로운 항목이 들어올 때까지 무한정 대기하기 때문이다.
따라서, 이러한 무한 루프를 막고자, PQ가 empty 상태가 되면 루프를 멈추고, 사용한 간선의 개수를 통해 최소 신장 트리가 형성되는지 판별해야 한다.