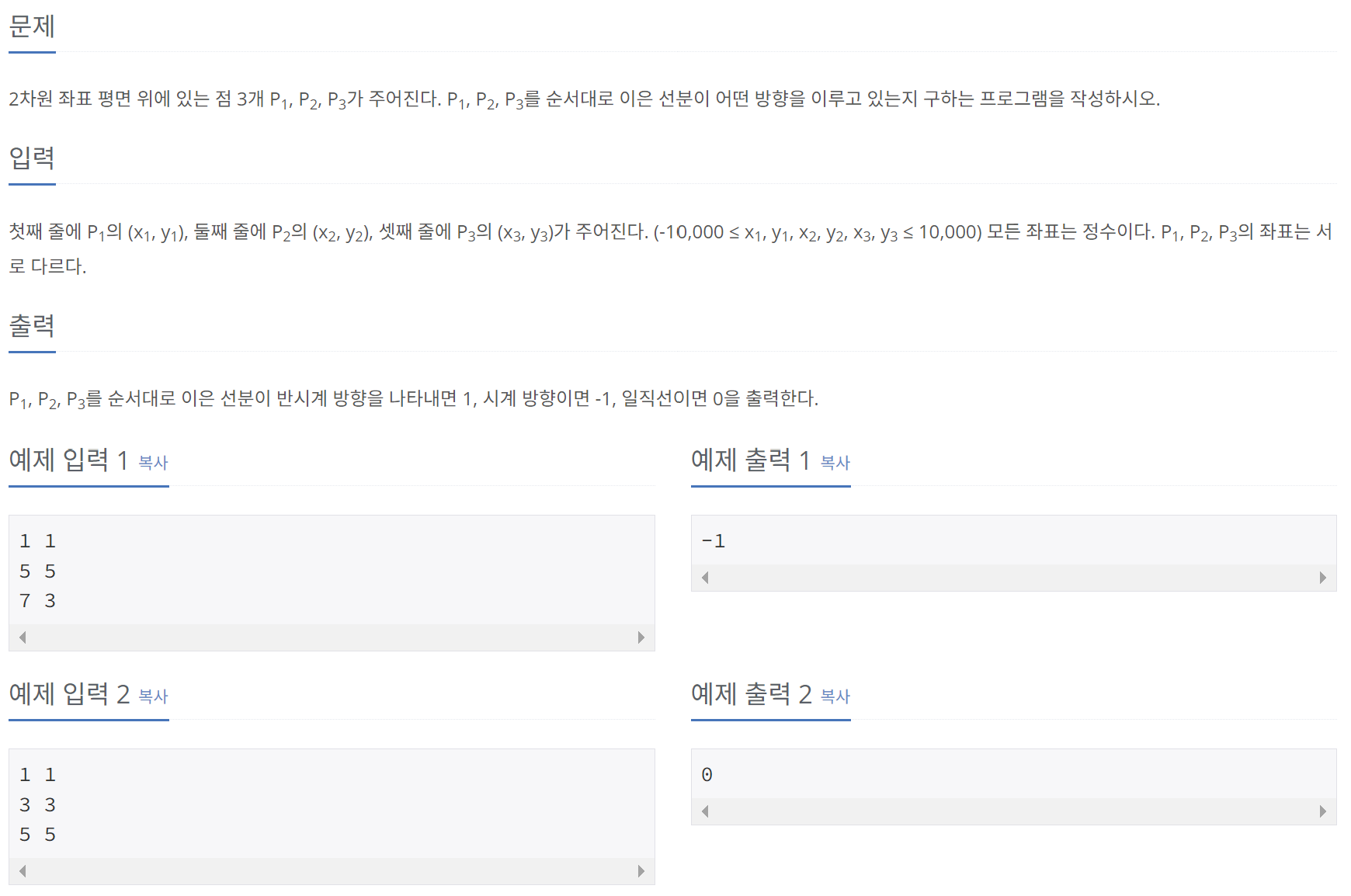
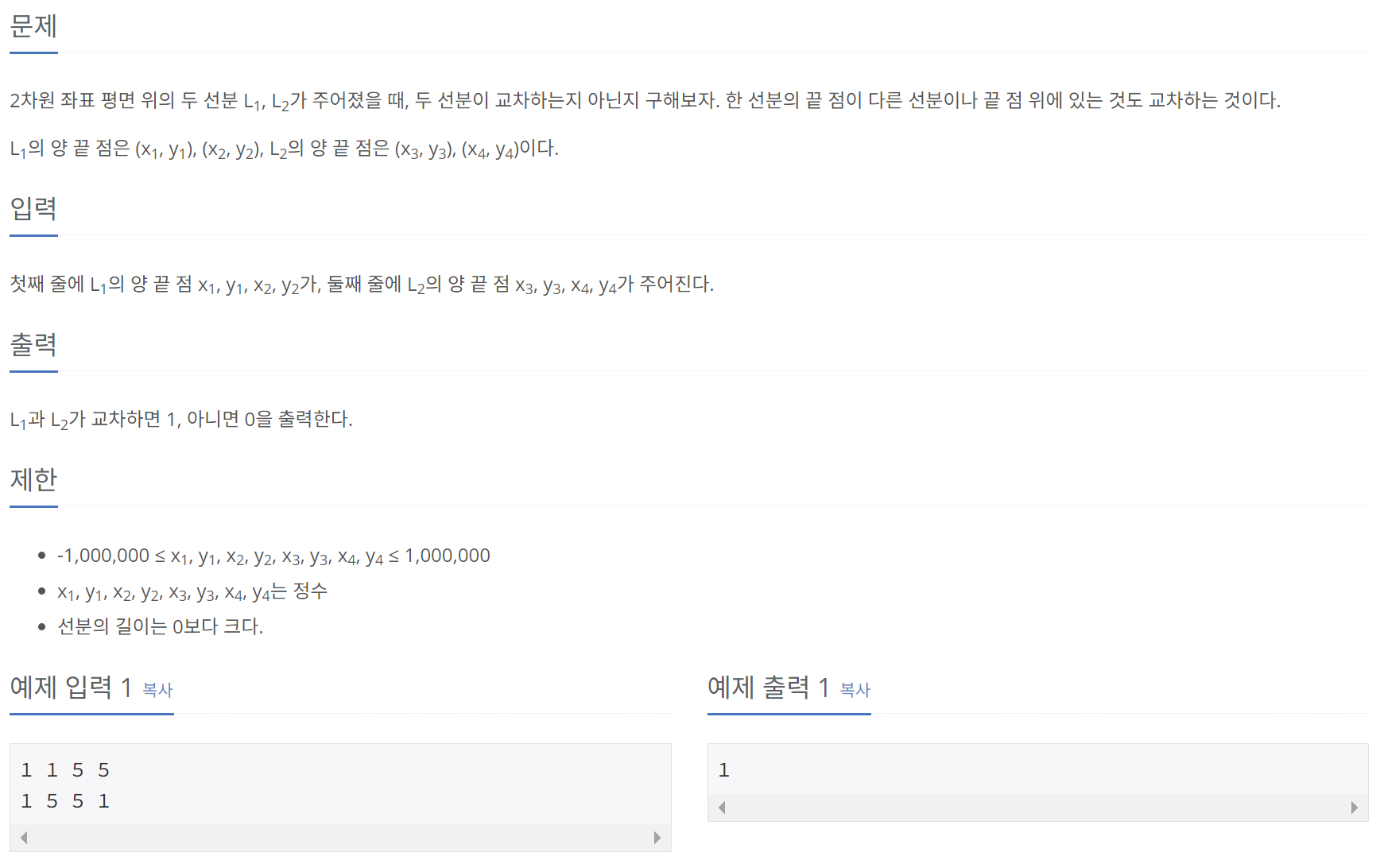
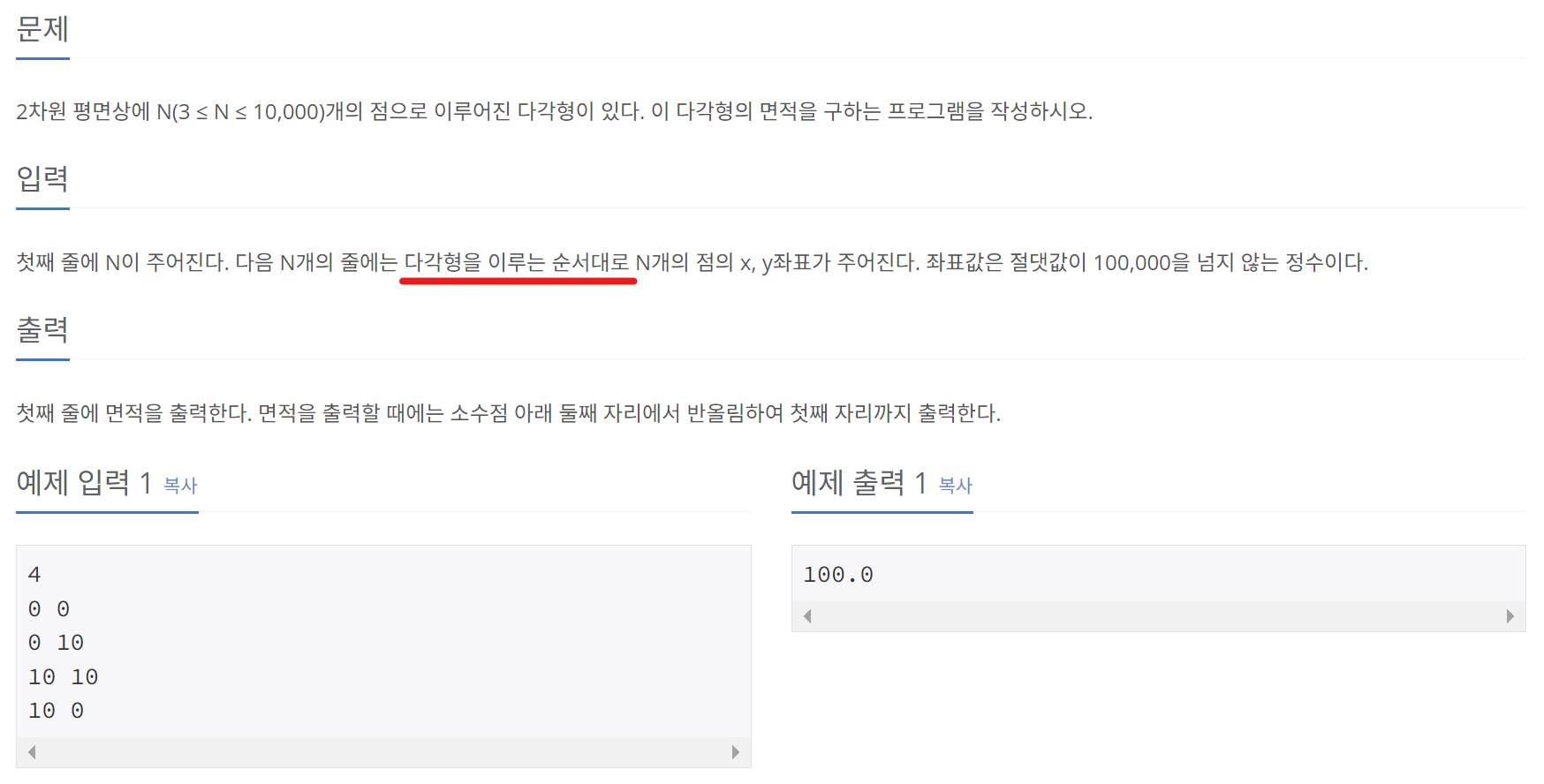
1. CCW
기하 관련 문제를 풀이할 때, 필수적으로 알아두어야 하는 알고리즘으로 CCW(Counter-Clockwise, 반시계 방향)가 있다. 여기서 CCW란, 벡터의 외적을 이용하여 3개의 점에 대한 위치 관계를 판단하는 알고리즘을 말한다.
예를 들어 아래와 같이 3개의 점이 주어졌다고 하자. 이 3개의 점은 다시 2개의 벡터로 나타낼 수 있다.
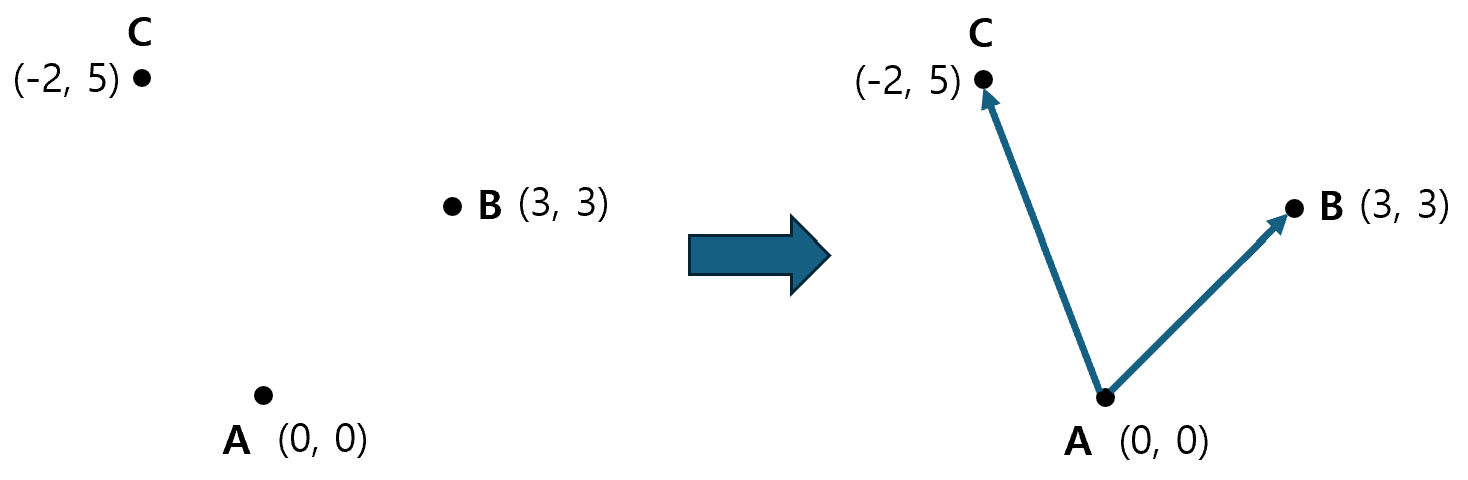
이 때, 이 두 벡터의 외적 값이 바로 CCW가 된다. 참고로, 2차원 평면에서 두 벡터의 외적은 스칼라 값으로 계산되며, 계산하는 방법(신발끈 공식)은 아래와 같다.

이제 CCW를 이용하여, 주어진 세 점의 위치 관계를 파악해보자.
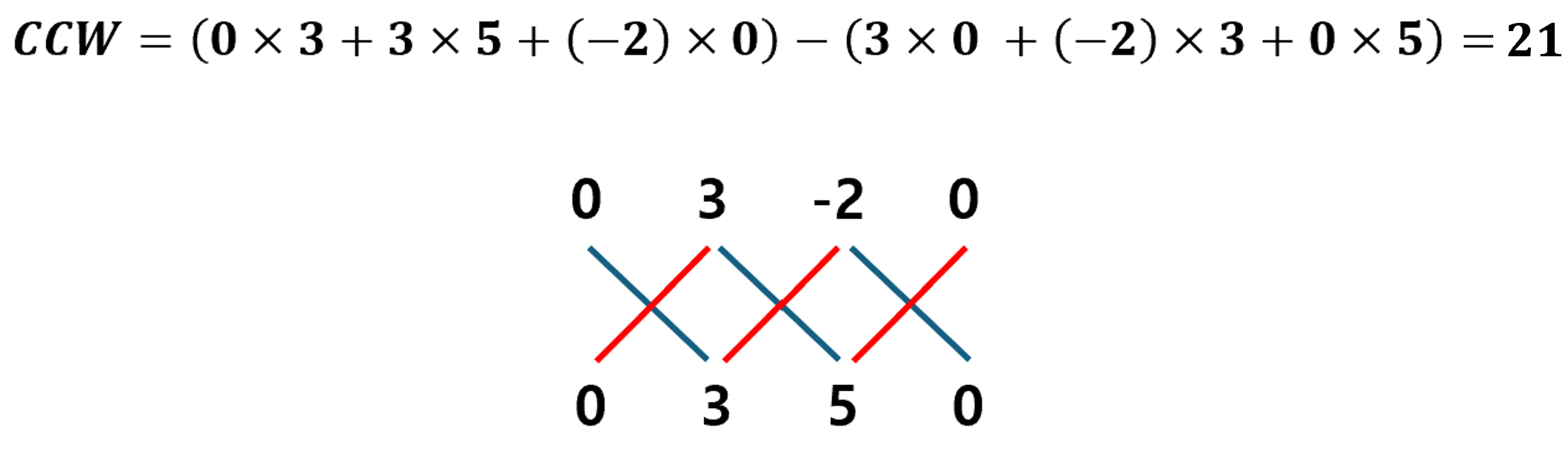
CCW의 값이 21이 나왔다. CCW 값의 의미는 아래와 같다.
① CCW > 0
- 점 A, B, C가 반시계 방향으로 놓여 있다.
② CCW = 0
- 점 A, B, C가 일직선 상의 점이다.
③ CCW < 0
- 점 A, B, C가 시계 방향으로 놓여 있다.
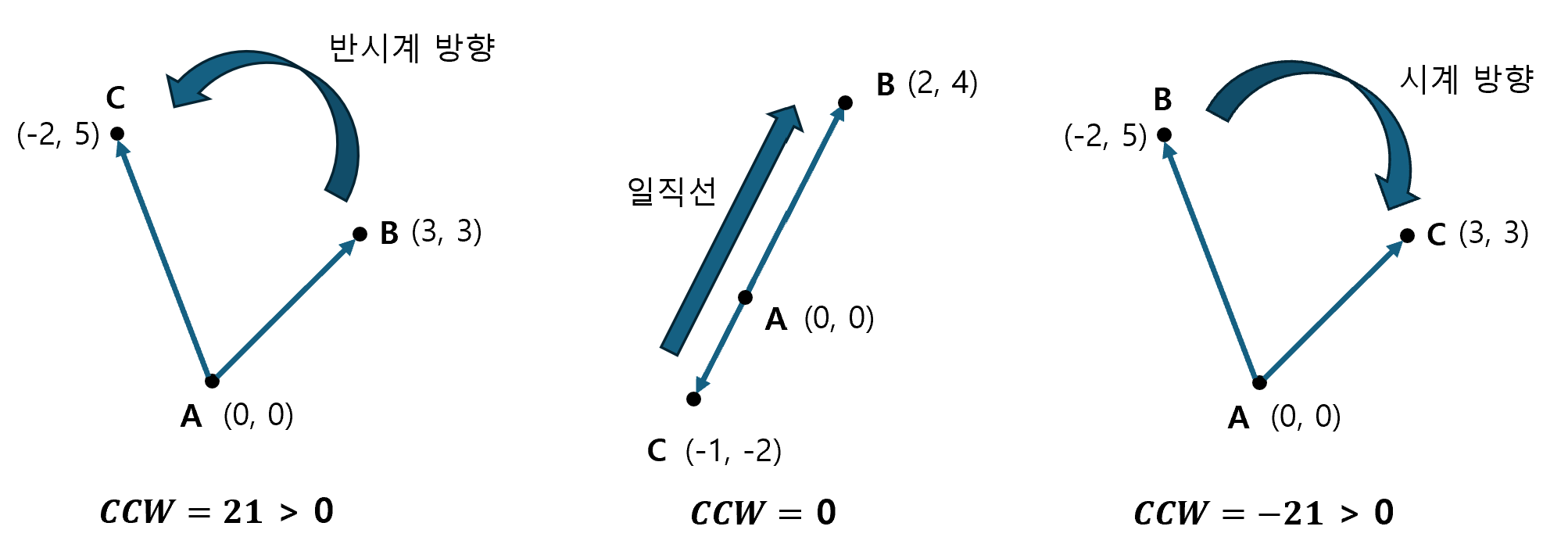
참고로, 이 알고리즘의 이름이 Counter-Clockwise인 이유는 반시계 방향을 양의 방향으로 간주하기 때문이다.
또한, CCW 값의 크기(절대값)는 두 벡터를 이웃한 변으로 갖는 평행사변형의 넓이가 되며, {CCW 값의 크기 / 2}는 세 점을 꼭짓점으로 갖는 삼각형의 넓이가 된다.
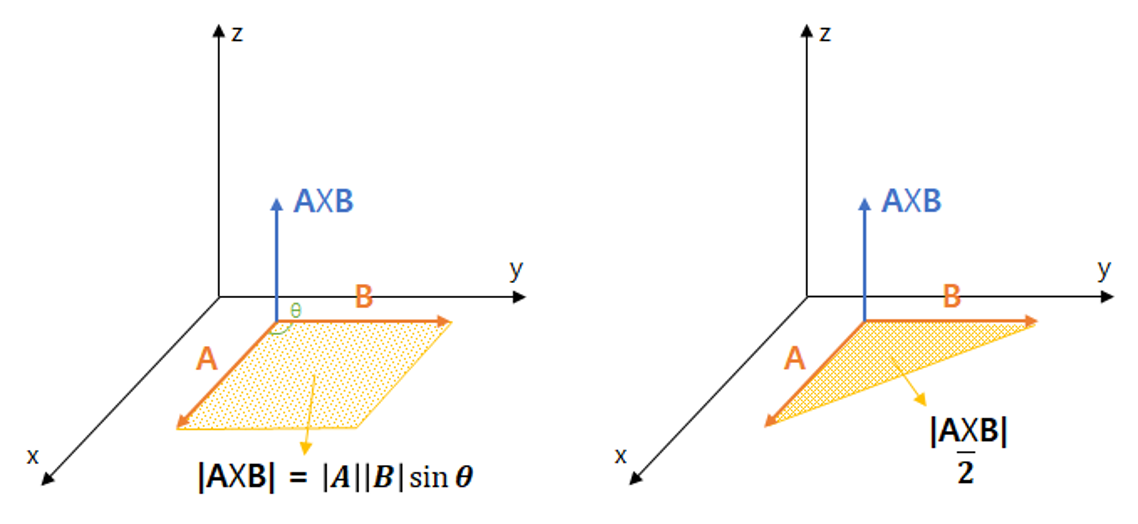
위 내용은 벡터의 외적을 배웠다면, 이미 알고 있을만한 내용이므로 자세한 설명은 생략하기로 하겠다.
2. 문제 풀이
1) 선분 방향 구하기
CCW의 기본 개념을 이용하는 문제이다. 아래의 코드는 기하 관련 문제 풀이에서 기본이 되는 내용이기 때문에 암기해 둘 것을 권장한다.
import sys
input = sys.stdin.readline
x1, y1 = map(int, input().split())
x2, y2 = map(int, input().split())
x3, y3 = map(int, input().split())
ccw = (x1 * y2 + x2 * y3 + x3 * y1) - (x2 * y1 + x3 * y2 + x1 * y3)
if ccw > 0 :
print(1)
elif ccw == 0:
print(0)
else:
print(-1)2) 선분의 교차 여부 구하기
이 문제도 CCW를 이용하여 풀이할 수 있는 문제이다. 선분이 교차하는 경우는 아래의 두 가지 경우로 나누어 생각할 수 있다.
- 두 선분이 겹치는 경우
- 두 선분이 한 지점에서 교차하는 경우
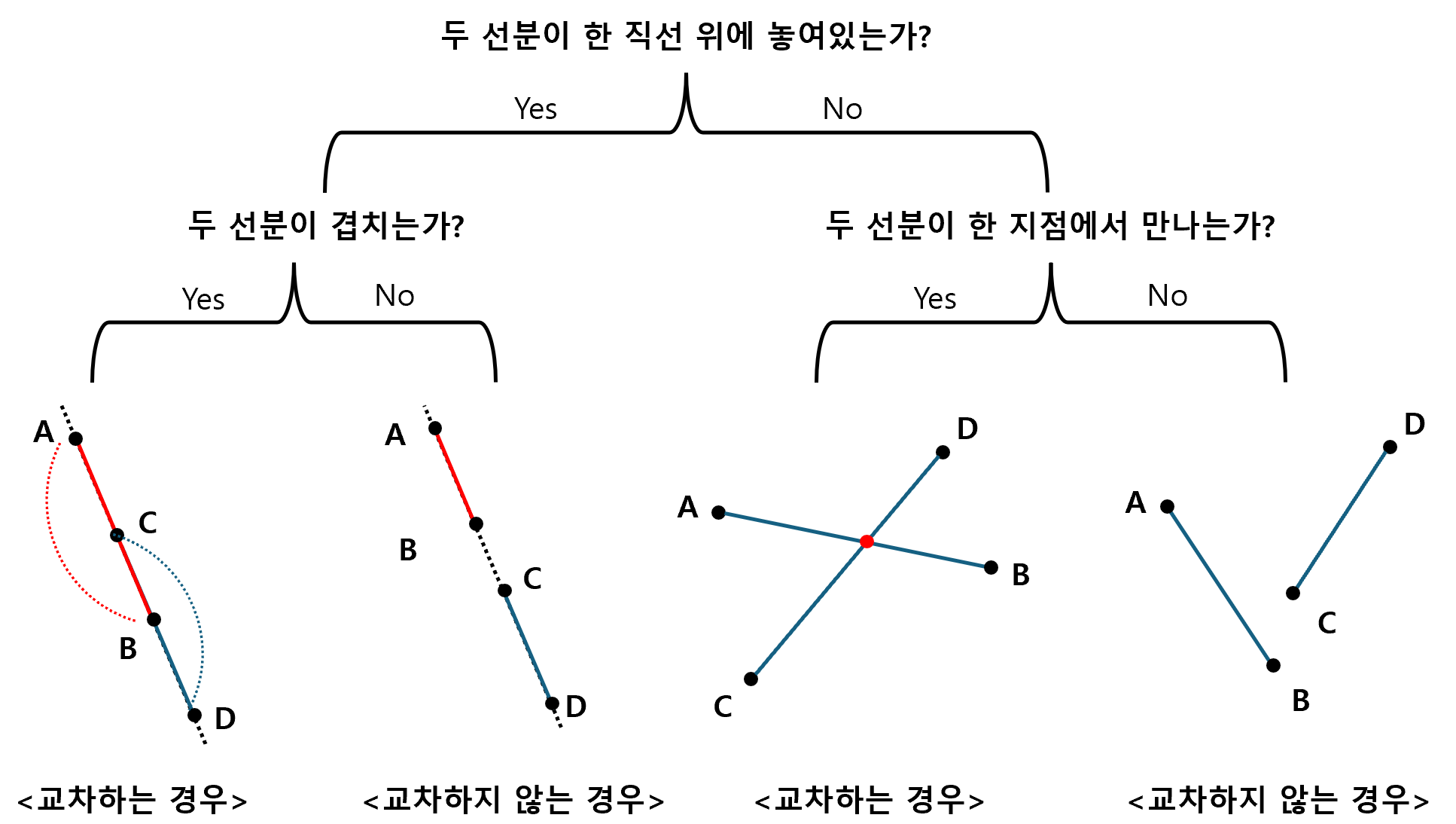
① 두 선분이 겹치는 경우
- 아래의 두 조건이 모두 성립할 때, 두 선분은 한 직선 위에 놓이게 된다.
- A-B 선분을 기준으로, 점 C와 D에서 구해진 CCW 값의 곱이 0
- C-D 선분을 기준으로 점 A와 B에서 구해진 CCW 값의 곱이 0
- 일직선 위의 점이라는 사실을 확인했다면, 이제 두 선분이 겹치는지 여부를 확인해야 한다.
- 두 선분이 겹치려면, 선분 A-B의 x의 최소 값이 선분 C-D의 x의 최대값보다 작아야 하며, A-B의 x의 최대 값은 C-D의 x의 최소값보다 커야 한다. (y에 대해서도 동일한 조건을 적용한다.)
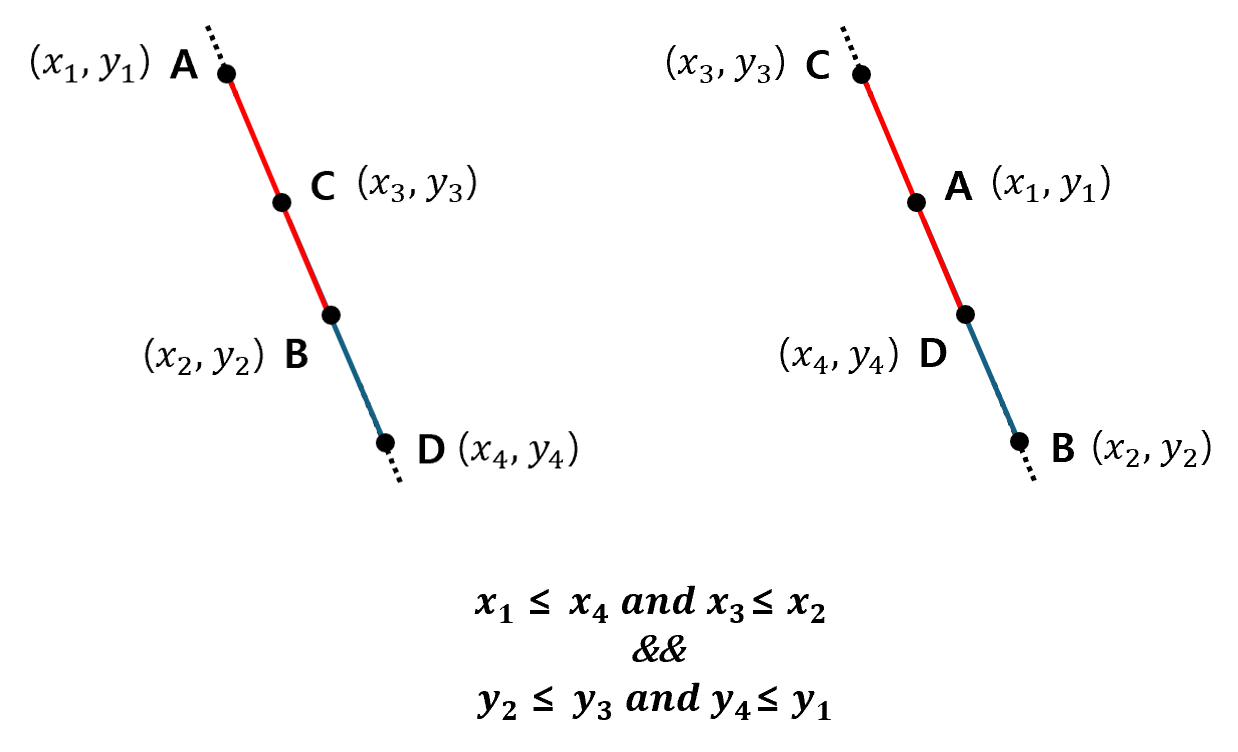
② 두 선분이 한 지점에서 교차하는 경우
-
아래의 두 조건이 모두 성립할 때, 두 선분은 한 지점에서 교차하게 된다.
- A-B 선분을 기준으로, 점 C와 D에서 구해진 CCW의 부호가 반대
- C-D 선분을 기준으로, 점 A와 B에서 구해진 CCW의 부호가 반대
-
CCW의 부호가 반대인지 확인하는 방법은, 두 CCW의 곱이 음수인지 확인하는 것이다.
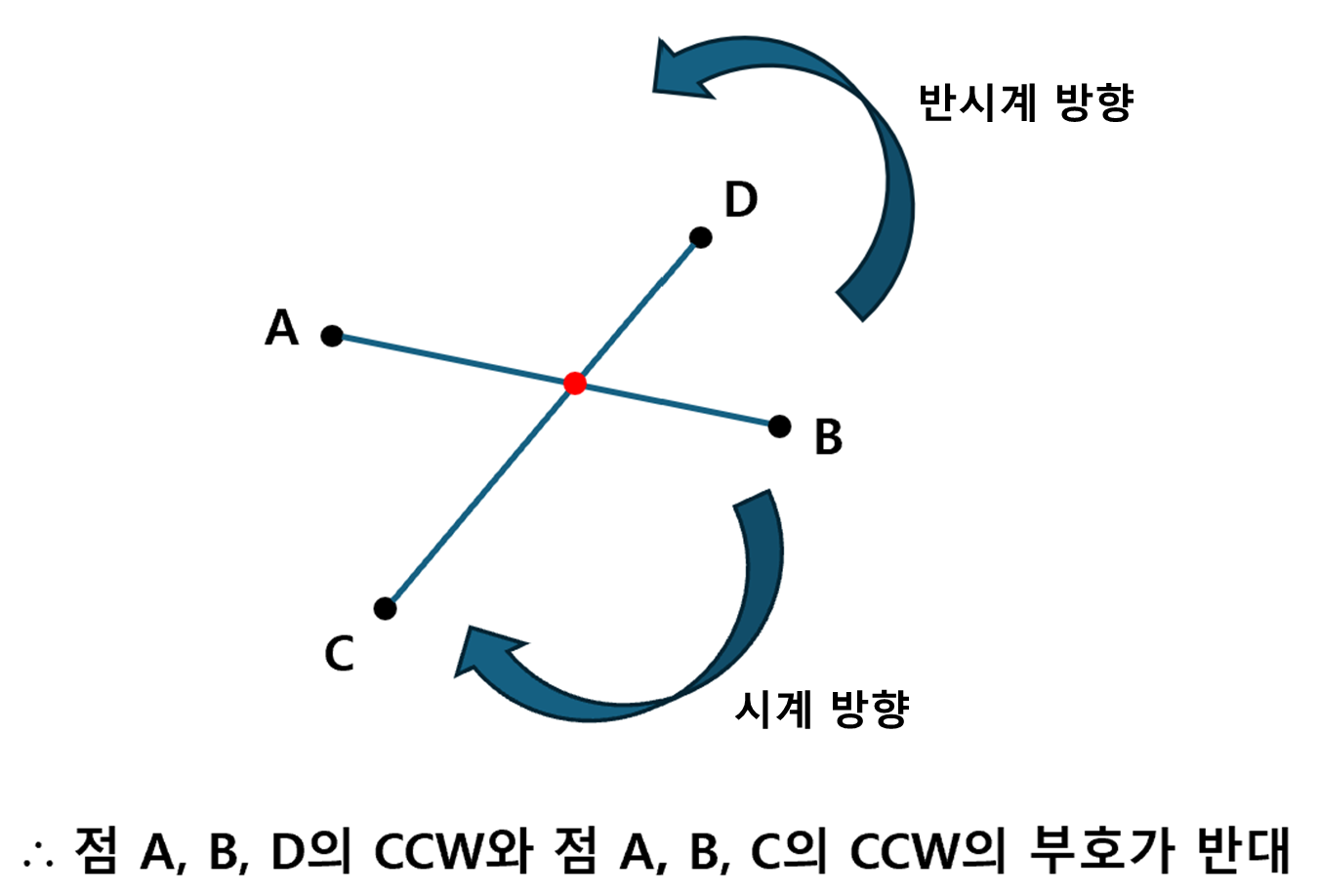
-
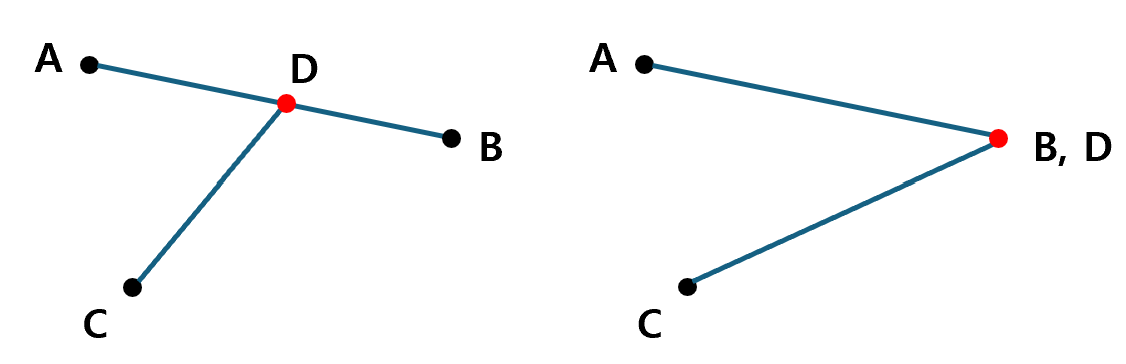
아래의 두 조건을 모두 만족하는 경우도, 한 선분의 끝점이 다른 선분 위에 있다는 의미이므로, 교차로 간주한다.
- A-B 선분을 기준으로, 점 C와 D에서 구해진 CCW의 곱이 0 (두 CCW 중 하나가 0인 경우)
- C-D 선분을 기준으로, 점 A와 B에서 구해진 CCW의 곱이 0 (두 CCW 중 하나가 0인 경우)
이제 위 내용을 적용하여 문제를 풀어보자.
import sys
input = sys.stdin.readline
x1, y1, x2, y2 = map(int, input().split())
x3, y3, x4, y4 = map(int, input().split())
def CCW(x1, y1, x2, y2, x3, y3):
ccw = (x1 * y2 + x2 * y3 + x3 * y1) - (x2 * y1 + x3 * y2 + x1 * y3)
if ccw > 0 :
return 1
elif ccw == 0:
return 0
else:
return -1
def isCross(x1, y1, x2, y2, x3, y3, x4, y4):
# A-B 선분을 기준으로 점 C와 D의 CCW 값을 구함
abc = CCW(x1, y1, x2, y2, x3, y3)
abd = CCW(x1, y1, x2, y2, x4, y4)
# C-D 선분을 기준으로 점 A와 B의 CCW 값을 구함
cda = CCW(x3, y3, x4, y4, x1, y1)
cdb = CCW(x3, y3, x4, y4, x2, y2)
if abc * abd == 0 and cda * cdb == 0: # 두 CCW의 곱이 모두 0이면, 이는 두 선분이 한 직선 위에 놓임을 의미
return isOverlab(x1, y1, x2, y2, x3, y3, x4, y4) # 두 선분이 겹치는지 여부를 파악
elif abc * abd <= 0 and cda * cdb <= 0: # 각 CCW의 부호가 반대가 되거나, 각 CCW 중 하나라도 0인 경우 두 선분이 한 지점에서 교차함
return True
else:
return False
def isOverlab(x1, y1, x2, y2, x3, y3, x4, y4):
if min(x1, x2) <= max(x3, x4) and max(x1, x2) >= min(x3, x4) \
and min(y1, y2) <= max(y3, y4) and max(y1, y2) >= min(y3, y4):
return True
return False
if isCross(x1, y1, x2, y2, x3, y3, x4, y4):
print(1)
else:
print(0)3) 다각형의 넓이 구하기
이 문제는 CCW의 크기를 반으로 나누어 준 값이 삼각형의 넓이가 된다는 사실을 이용해 풀이할 수 있다. 다각형의 넓이를 구하는 문제에서 왜 삼각형 넓이 공식을 사용해야 하는지 의문이 생길 수도 있는데, 이는 모든 다각형의 넓이를 삼각형의 넓이의 합으로 구성할 수 있기 때문이다.
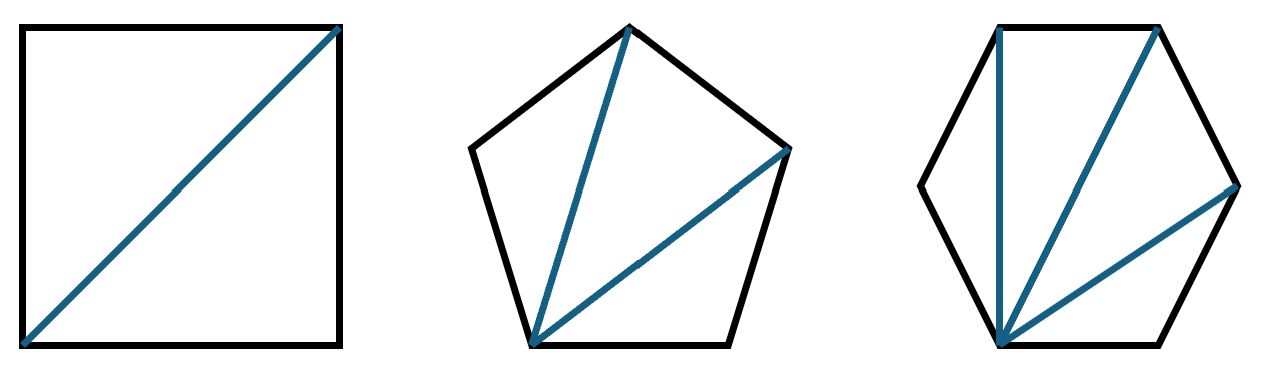
즉, 삼각형의 넓이를 구하는 공식을, 다각형으로 확장할 수 있다는 의미이다.
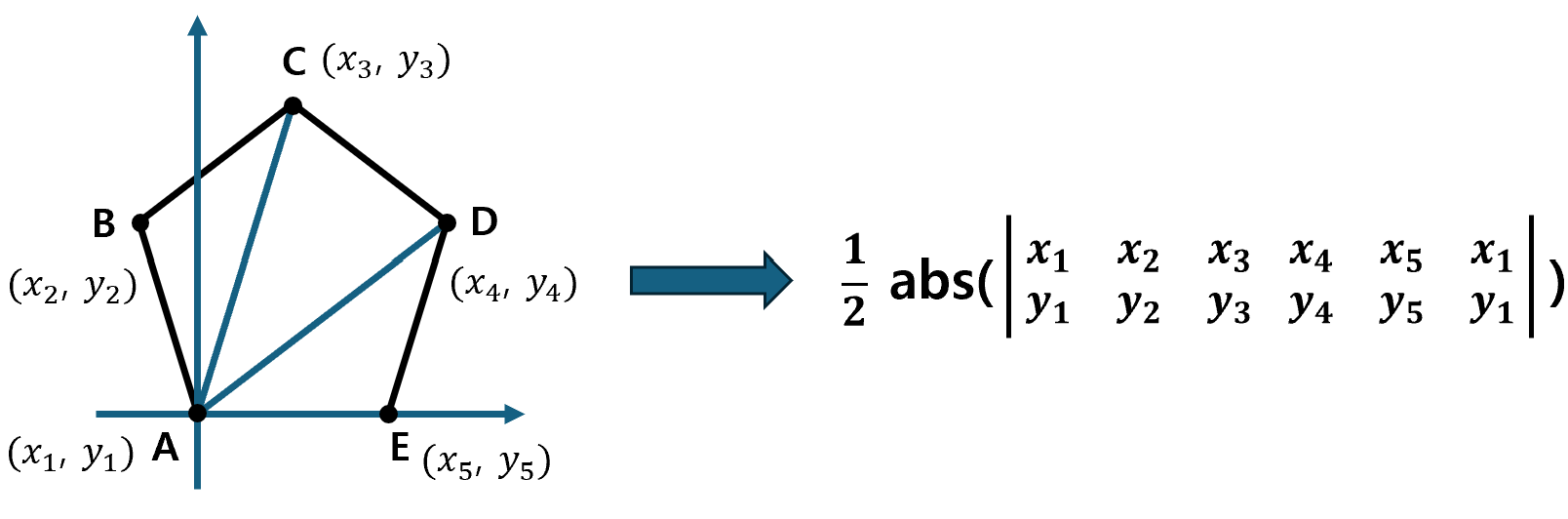
다만, 아래의 두 가지 사항에 대해서는 주의가 필요하다.
- 좌표가 반드시 다각형을 구성하는 순서대로 주어져야 한다.
- CCW의 값이 음수가 될 수 있으므로, CCW의 합(최종 외적의 결과)을 구한 후 마지막에 절대값을 취해주어야 한다.
다행히 문제의 조건으로, 좌표가 다각형을 구성하는 순서대로 주어진다는 사실이 명시되어 있다. 하지만, 좌표가 반시계방향으로 주어질 수도 있고, 시계방향으로 주어질 수도 있기 때문에 절대값을 취하는 내용에 대해서는 여전히 주의가 필요하다. 위 내용을 바탕으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
N = int(input())
lst_x = []
lst_y = []
for i in range(N):
x, y = map(int, input().split())
lst_x.append(x)
lst_y.append(y)
# 외적을 계산하기(신발끈 공식을 사용하기) 위해선 첫째항을 마지막에 추가해야 함
lst_x.append(lst_x[0])
lst_y.append(lst_y[0])
plus = 0
minus = 0
for i in range(N): # 신발끈 공식(좌표의 개수 = 신발끈 개수)
# 편의상 +항과 -항을 따로 계산
plus += (lst_x[i] * lst_y[i + 1])
minus += (lst_x[i + 1] * lst_y[i])
answer = 0.5 * abs(plus - minus) # 절대값 주의
print(round(answer, 1)) # 소수점 이하 둘째자리에서 반올림하여 첫째자리까지 출력