1. Knapsack Problem
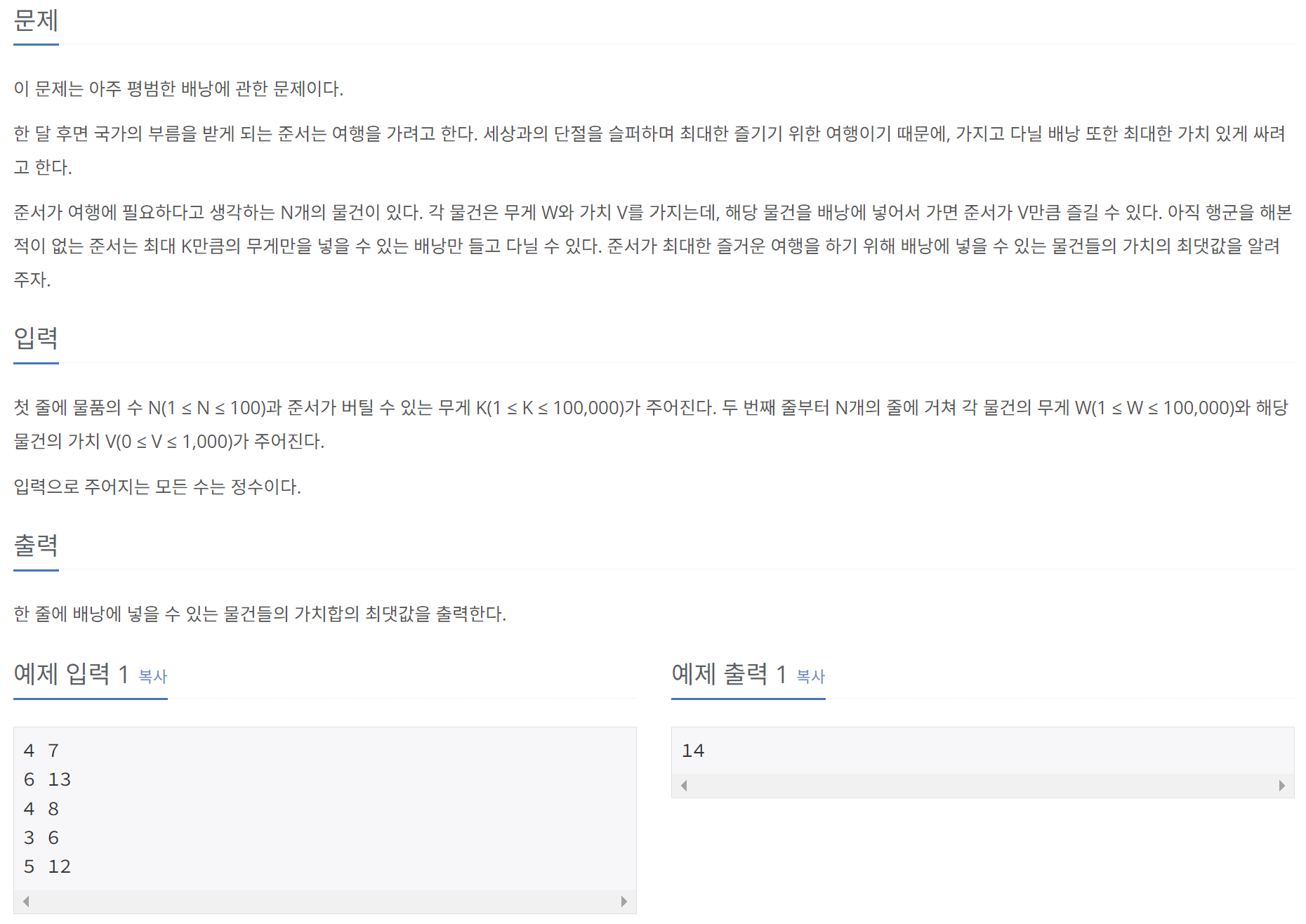
대표적인 DP 문제 중 하나로 Knapsack Problem을 생각할 수 있다. 여기서 Knapsack 문제란, 주어진 무게 한도 내에서 물건들을 배낭에 담아 최대의 가치를 얻는 방법을 찾는 문제를 말한다. 이 문제에서 DP 테이블은 아래와 같이 정의된다.
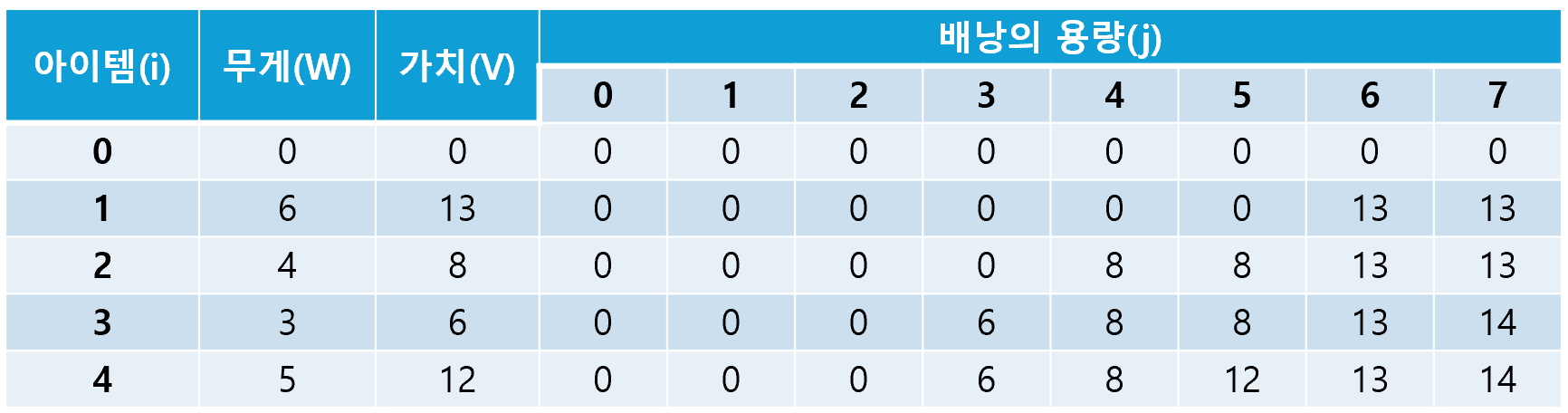
- D[i][j]: i개의 아이템을 용량이 j인 배낭에 넣어 얻을 수 있는 최대 가치
DP 테이블은 i번째 아이템을 선택했을 때의 가치와 선택하지 않았을 때의 가치 중 더 높은 값으로 업데이트된다. 단, i번째 아이템의 무게가 배낭의 용량보다 크다면, 해당 아이템은 고려하지 않는다.
if j < W: # 아이템의 무게가 배낭의 용량보다 큰 경우
D[i][j] = D[i - 1][j] # 해당 아이템을 고려하지 않음.
else: # i번째 아이템을 고려하지 않은 경우와 고려한 경우 중 더 가치가 높은 것을 선택
D[i][j] = max(D[i - 1][j], V + D[i - 1][j - W])한 가지 주의해야 할 것은 DP 테이블의 (i - 1)번째 인덱스에서 IndexError가 발생하지 않도록 DP 테이블에 Zero Padding을 적용해야 한다는 것이다.
이제 배운 내용을 바탕으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
D = [[0 for _ in range(K + 1)] for _ in range(N + 1)]
for i in range(1, N + 1): # i번째 아이템
W, V = map(int, input().split())
for j in range(1, K + 1): # 배낭의 용량 j
if j < W: # 아이템의 무게가 배낭의 용량보다 큰 경우
D[i][j] = D[i - 1][j] # 해당 아이템을 고려하지 않음.
else: # i번째 아이템을 고려하지 않은 경우와 고려한 경우 중 더 가치가 높은 것을 선택
D[i][j] = max(D[i - 1][j], V + D[i - 1][j - W])
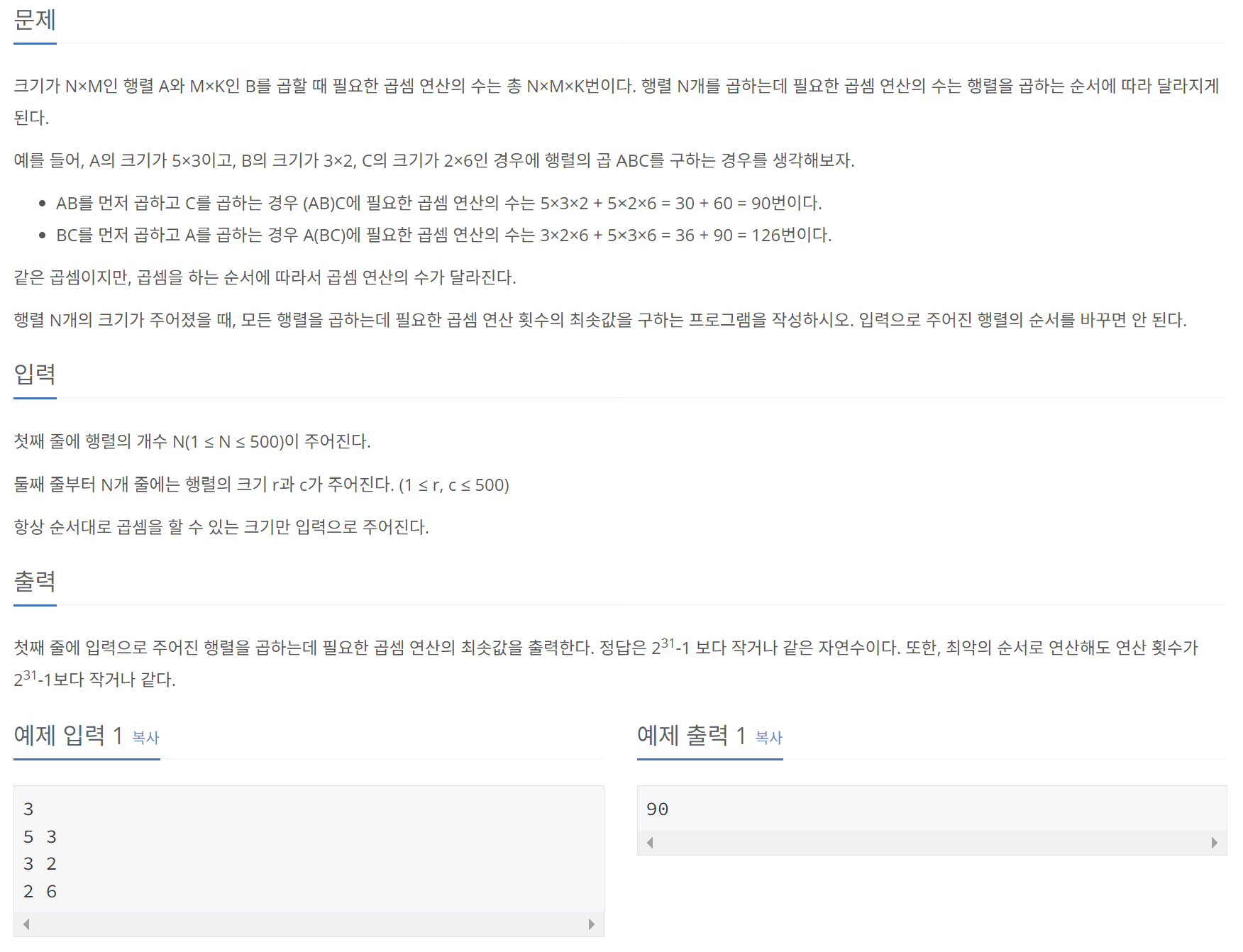
print(D[N][K])2. 행렬 곱 연산 횟수의 최솟값 구하기
연쇄 행렬 곱셈(Matrix Chain Multiplication) 문제도 대표적인 DP 문제이다. 이 문제의 점화식을 도출하기 위해서는 행렬 곱의 두 가지 성질을 이해해야 한다.
① N개의 행렬 곱을 계산할 수 있는 경우의 수는 N - 1이다.
- 예를 들어 5개의 행렬에 대해 행렬 곱을 수행할 수 있는 경우의 수는 아래의 4가지뿐이다.

② 두 행렬의 곱셈에서 첫 행렬의 열과 둘째 행렬의 행의 개수가 같다
이 두 가지 성질을 이용하여 점화식을 도출해보자. (velog에서는 아래 첨자 사용이 어렵기 때문에 이미지로 설명을 대체한다.)

위 내용을 바탕으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
N = int(input())
D = [[sys.maxsize for i in range(N)] for j in range(N)] # 최소 값을 구할 때는 maxsize로 초기화
lst = [] # 행렬 리스트
for i in range(N):
row, col = map(int, input().split())
lst.append([row, col])
for i in range(N): # D[i][j]에서 i == j이면, 행렬이 하나라는 의미이므로 필요한 연산의 수는 0이 됨.
D[i][i] = 0
# 이 부분에 대해서는 아래의 설명 참고
for cnt in range(2, N + 1): # i와 j 사이의 존재하는 행렬의 개수(i와 j 행렬도 포함)
for i in range(N - cnt + 1):
j = i + cnt - 1
for k in range(i, j):
D[i][j] = min(D[i][k] + D[k + 1][j] + lst[i][0] * lst[k][1] * lst[j][1], D[i][j])
print(D[0][N - 1]) # 인덱스가 0부터 시작하므로, 0번 행렬부터 N-1번 행렬까지의 최소 연산 횟수로 구해야 함.위 코드의 3중 for문 부분에 대해 설명하도록 하겠다. 최외곽 for 문에서 i와 j 사이의 간격을 1씩 늘려간다. 이미 i와 j가 같은 경우에 대해서는 위에서 처리해주었기 때문에 cnt는 2부터 시작하며, cnt의 최대 값은 i와 j의 최대 간격인 N이 된다(여기서, 간격은 j - i + 1로 정의된다).
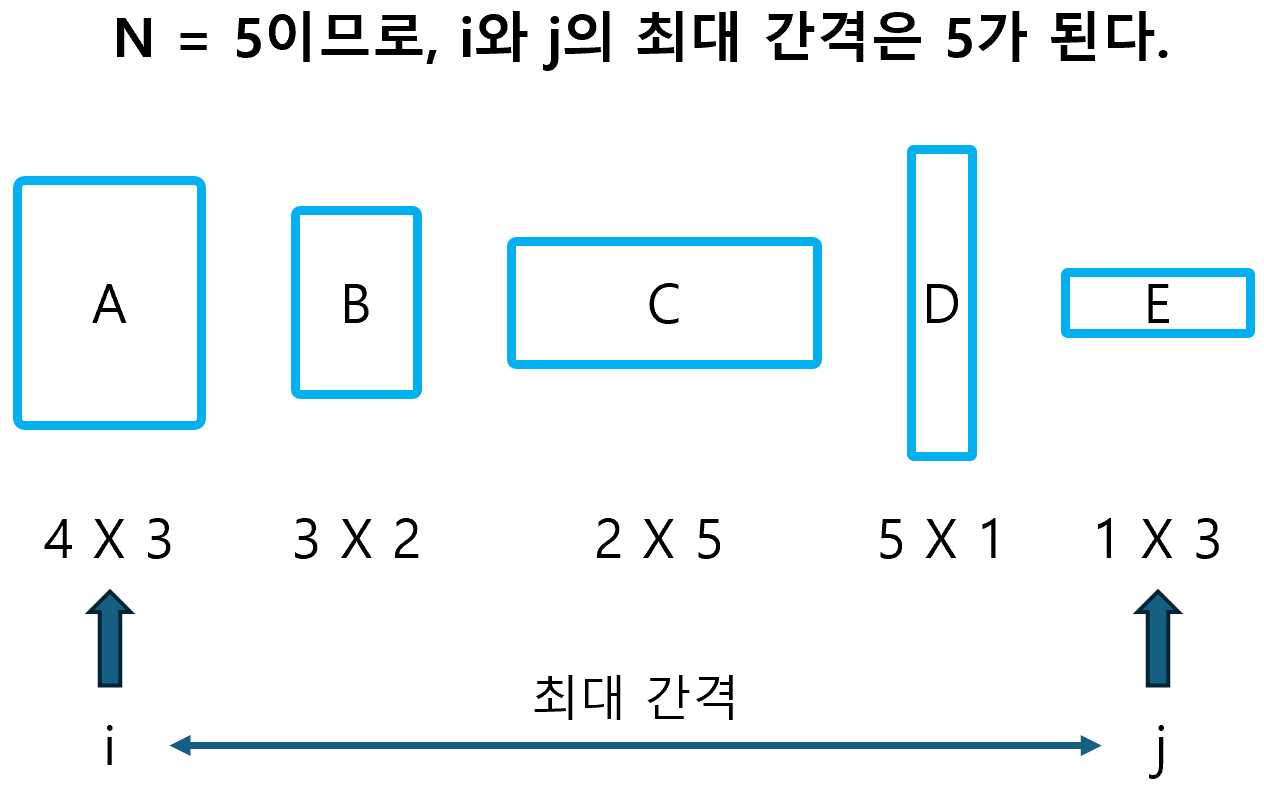
cnt가 2인 상황을 가정해보자. 그러면, 아래의 4가지 경우를 모두 고려해주어야 한다.
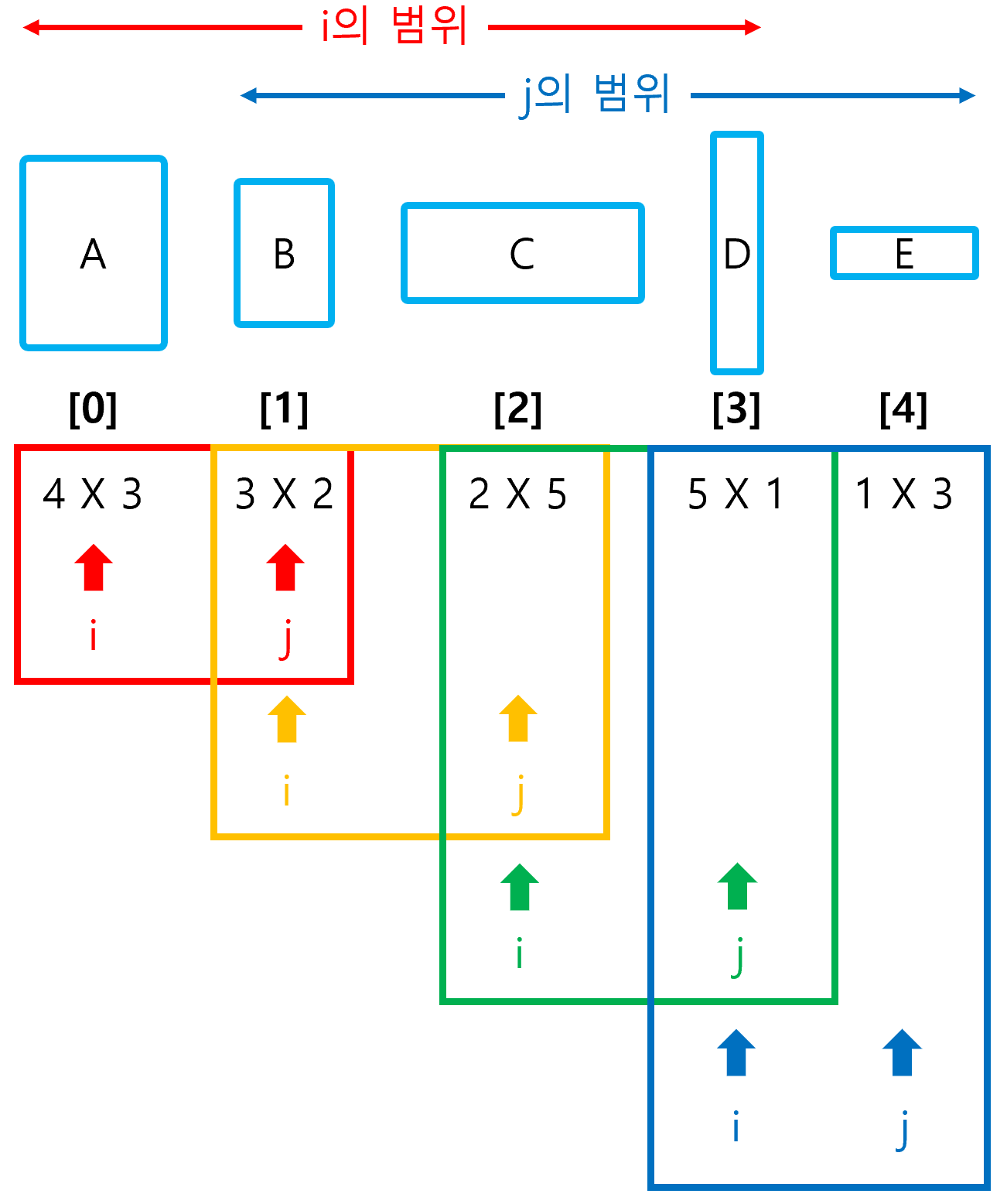
위 그림에서 알 수 있듯 i의 범위는 0부터 5 - cnt까지이고, j는 i + cnt - 1로 결정된다는 것을 알 수 있다. 이렇게 선정된 i와 j 사이에 존재하는 모든 값(k)을 반복하여 최소 연산 횟수를 얻어내는 것이다.
위 코드를 제출했더니, 시간 초과가 발생했다. 다행히 PyPy3로 제출하니 문제가 해결되었다. 아무래도 N이 500일 때, 3중 for문에 의해 1.25억번의 연산이 수행되면서 시간 초과가 발생한 것 같다.
그러나 DP 문제는 시간 제약으로부터 비교적 자유롭기 때문에, 시간 복잡도를 고려하지 않아도 되는 경우가 많다. 그래서, 이 문제도 시간 초과에 대해서는 크게 신경 쓰지 않아도 될 것 같다. 비록 시간 초과가 발생하긴 했지만, 연쇄 행렬 곱셈 문제는 3중 for문을 이용한 풀이가 가장 직관적이기 때문에, 다른 방식으로 수정할 필요는 없을 것 같다. 따라서, 이렇게 풀이를 마무리하기로 한다.
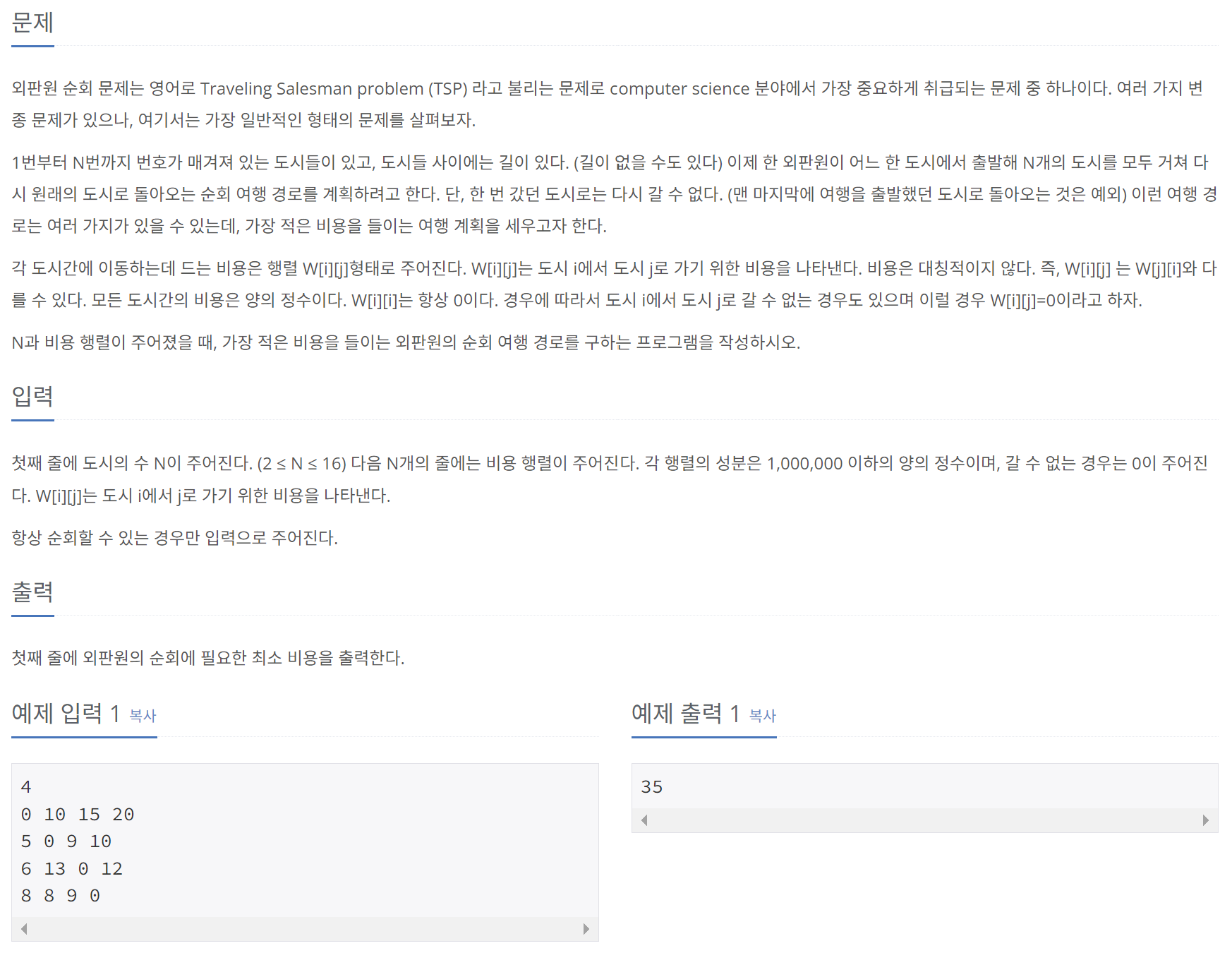
3. 외판원의 순회 경로 짜기
TSP(최적 일주 경로) 역시 DP의 대표적인 문제이면서, 물류나 딥러닝 분야 등에 활용될만큼 중요한 문제이다. TSP의 점화식은 아래와 같이 정의된다.

위 점화식의 정의를 보면, 아래의 두 가지 의문이 생길 것이다.
① "부분 집합 A를 어떻게 표현할 수 있는가?"
- 다양한 방법이 있겠지만, 여기서는 비트 마스킹 방식을 사용할 것이다.
- 즉, 2진수의 각 자리수를 정점 번호라 생각하여 visited(1) 또는 not_visited(0)를 저장하겠다는 의미이다.

② "시작 정점을 임의로 지정해도 되는가?"
- 문제에서 시작 정점을 지정해주지 않았지만, 시작 정점을 임의로 지정해도 전혀 문제가 없다.
- 그 이유는 최적의 경로가 사이클을 이루기 때문이다.
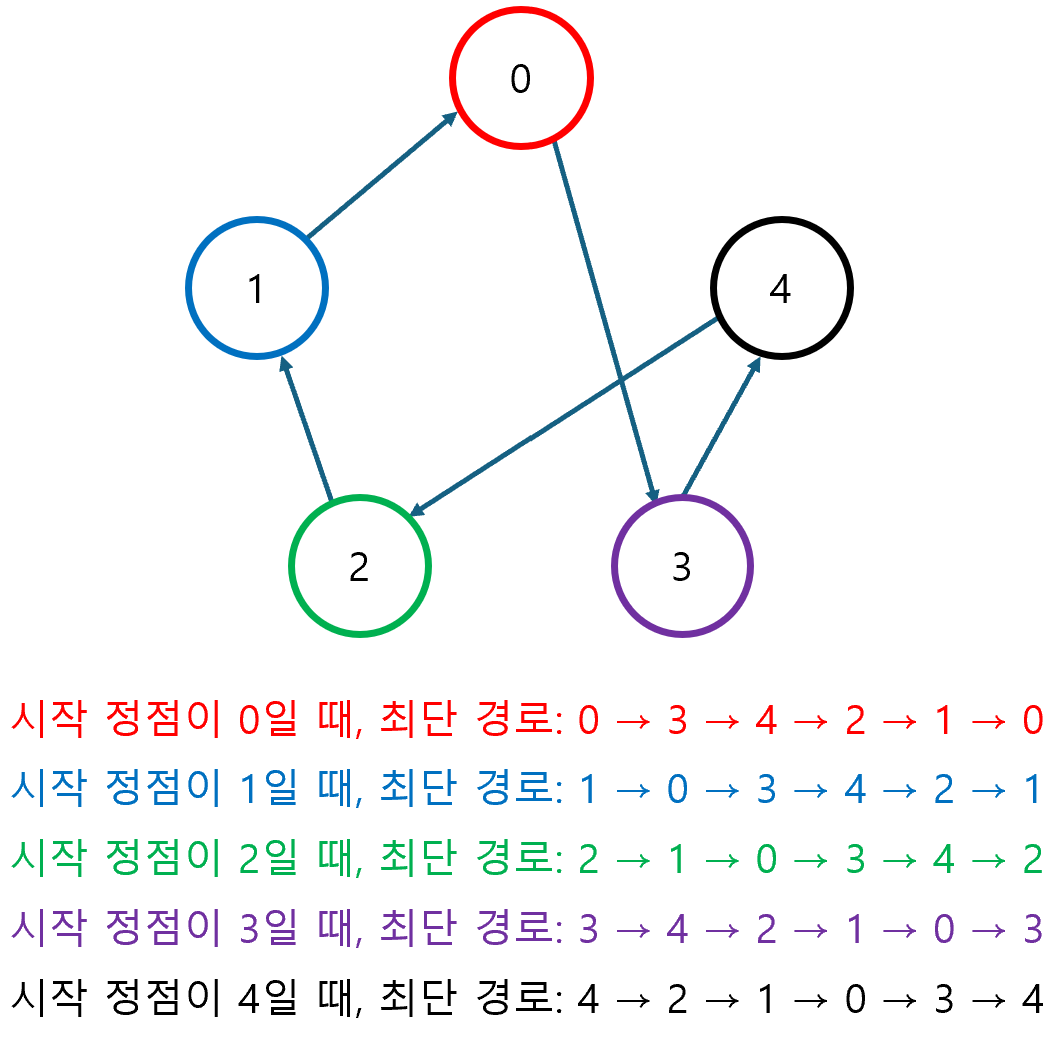
위 내용을 바탕으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
N = int(input())
W = [] # 노드 간 가중치 배열
for i in range(N):
W.append(list(map(int, input().split())))
ALL_VISITED = (1 << N) - 1 # ex) N이 4이면 10000 - 1 = 1111이 됨. 즉, 4개의 정점을 모두 방문했음을 의미
D = [[0 for i in range(1 << N)] for j in range(N)] # DP 테이블은 정점의 개수를 행으로, 부분 집합 A(비트 마스킹)를 열로 가짐.
def tsp(cur, visited):
if visited == ALL_VISITED: # 모든 정점 방문 완료
if W[cur][0] > 0: # 현재 정점에서 시작 정점으로 돌아갈 수 있는 경로가 있는 경우
return W[cur][0] # 해당 경로의 가중치를 반환
else:
return sys.maxsize
if D[cur][visited] is not 0: # Memoization(이미 저장된 값이 있다면, 저장된 값 재사용)
return D[cur][visited]
min_cost = sys.maxsize
for next in range(N):
# visited & (1 << next) == 0 → 비트 and 연산. next 노드가 아직 방문하지 않은 노드인지를 확인
# ex) 1101을 통해 2번 노드를 방문했는지 확인 → 1101 & (1 << 2) = 1101 & 100 = 0100 != 0이므로 이미 방문한 노드임.
# W[cur][next] > 0 → cur 노드에서 next 노드로의 경로가 존재하는지 확인
if visited & (1 << next) == 0 and W[cur][next] > 0:
new_cost = W[cur][next] + tsp(next, visited | (1 << next)) # visited에 1 << next를 더하여 next 노드 방문을 표시
min_cost = min(min_cost, new_cost) # cur, visited 상황에서 어떤 노드를 next 노드로 선택해야 비용이 최소가 되는지 결정
D[cur][visited] = min_cost
return min_cost
# 시작 정점을 임의로 0번 정점으로 지정. 출발 노드인 0번 노드를 방문했다는 의미로 0001을 전달.
print(tsp(0, 1)) 개인적으로 DP 문제를 Top-Down Approach로 풀이하는 것을 별로 좋아하지 않지만, 적어도 TSP 문제는 Top-Down Approach를 이용하여 풀이할 것을 권장한다. (Bottom-Up 방식보다 코드가 더 명확해지기 때문)
다만, Top-Down Approach를 사용할 때, 반드시 Memoization을 잊지 않도록 주의해야 한다. 점화식을 작성하면, 자동으로 Tabulation이 되는 Bottom-Up과 달리 Top-Down은 점화식과 별도로 Memoization을 작성해주어야 한다.
TSP 문제가 DP 문제 중에서도 꽤나 까다로운 유형에 속하는만큼 쉽지 않은 문제였던 것 같다.