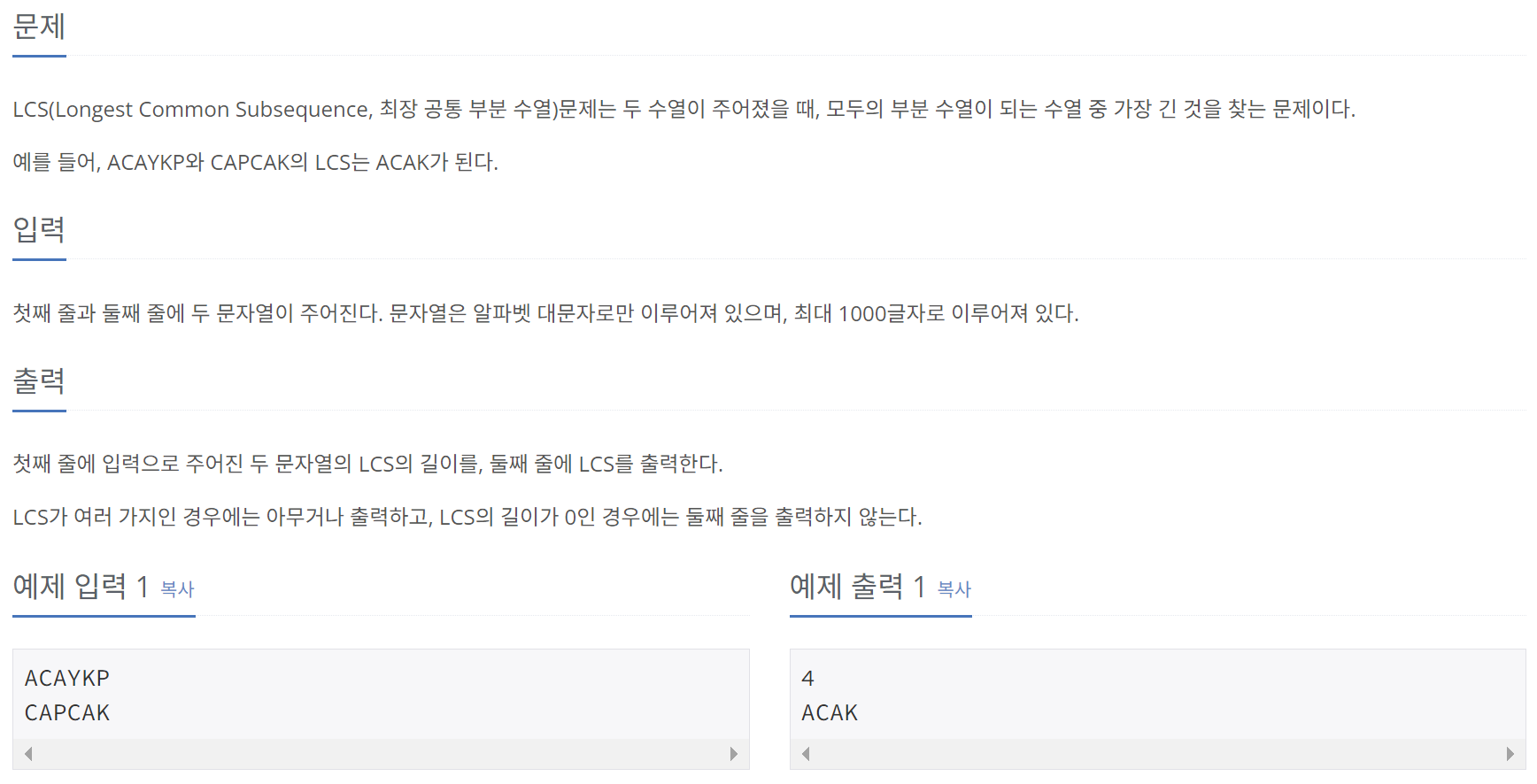
1. 최장 공통 부분 수열 찾기
여기서 말하는 부분 수열이란, 원래의 수열에서 순서를 유지하면서 만들어낼 수 있는 수열을 말한다. 예를 들어, 원래의 수열이 [A, B, C, D, E]일 때, 만들 수 있는 부분 수열에는 [A, B, C], [B, D, E], [A, E], [] 등이 있다.
특히 두 수열에 대한 공통 부분 수열 중, 길이가 가장 긴 수열을 LCS(최장 공통 부분 수열)라고 하는데, LCS 문제는 대표적인 DP 문제이다. LCS 문제를 풀이하는 기본적인 아이디어는 각 문자열을 행과 열로 갖는 테이블을 만드는 것에서부터 시작된다.
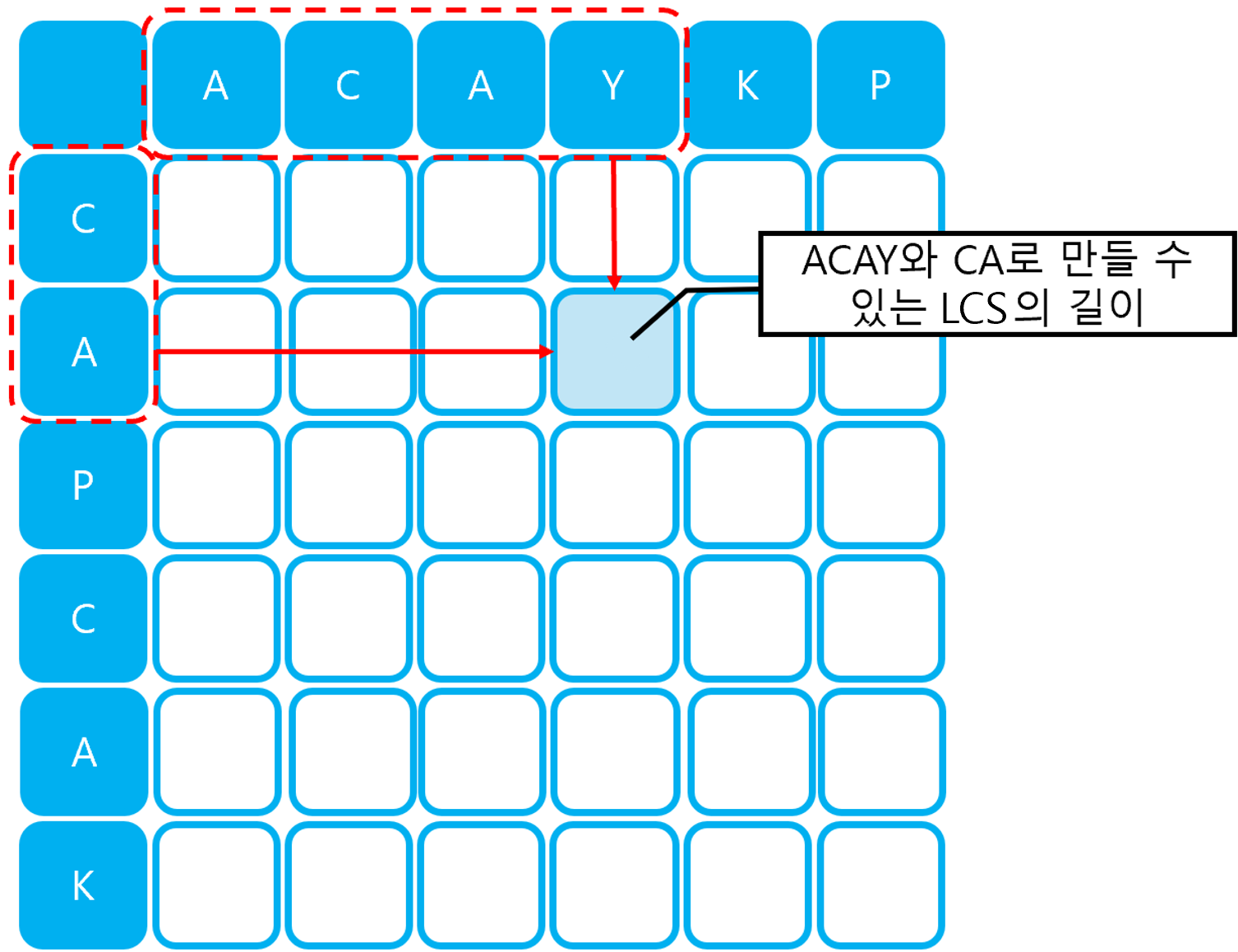
위 테이블이 DP 테이블이 되며, 테이블에 저장되는 값은 해당 인덱스까지의 두 수열로 만들 수 있는 LCS의 길이가 된다. LCS의 점화식은 두 가지 경우로 구분된다.
- 행과 열의 문자가 같은 경우
- 행과 열의 문자가 다른 경우
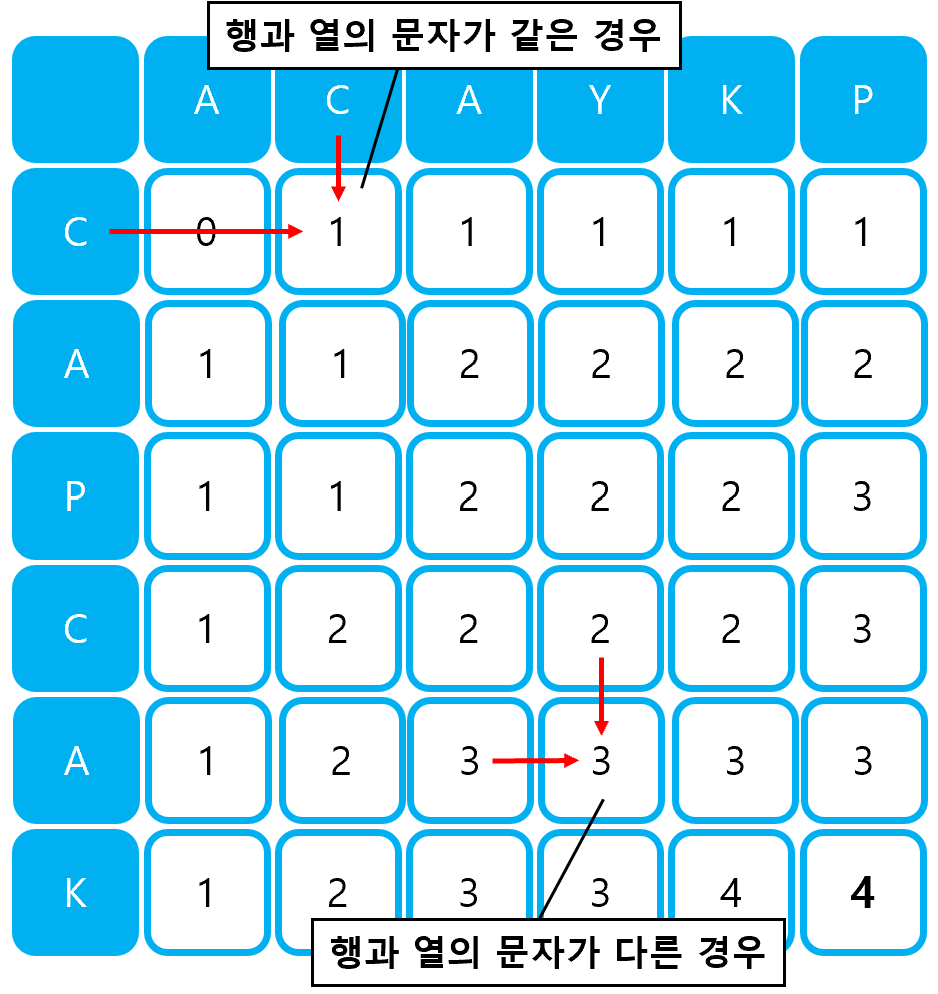
행과 열의 문자가 같다는 것은 LCS에 해당 문자가 포함된다는 의미이므로, 지난 LCS의 길이에서 1을 더해주면 된다. 즉, 점화식은 D[i][j] = D[i-1][j-1] + 1이 된다. 또한, 행과 열의 문자가 다르다는 것은 해당 문자가 LCS에 포함되지 않는다는 의미이므로, 해당 문자를 포함하기 이전 수열의 값 중 더 큰 값으로 LCS를 결정하면 된다. 즉, 점화식은 D[i][j] = max(D[i-1][j], D[i][j-1])이 된다.
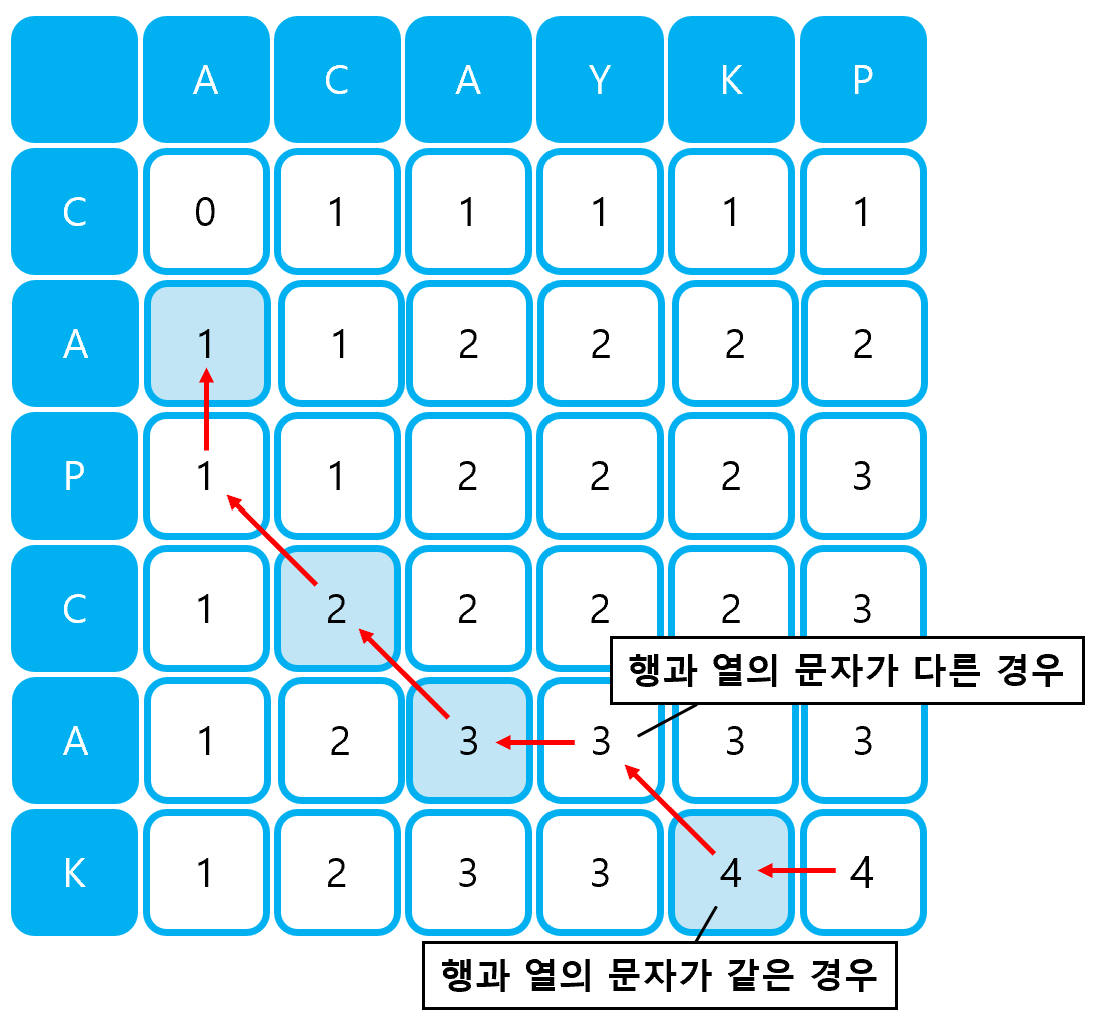
실제 LCS의 원소를 알아내기 위한 방법도 위 과정과 크게 다르지 않다. 테이블의 마지막 부분에서부터 시작하여, 행과 열의 문자가 같으면 그 값을 저장한 후 대각선 왼쪽으로 이동하고, 행과 열의 문자가 다르면 왼쪽과 위쪽 중 더 큰 값쪽으로 이동한다. 이제 저장된 값을 역순으로 출력하기만 하면 문제 풀이가 완료된다.
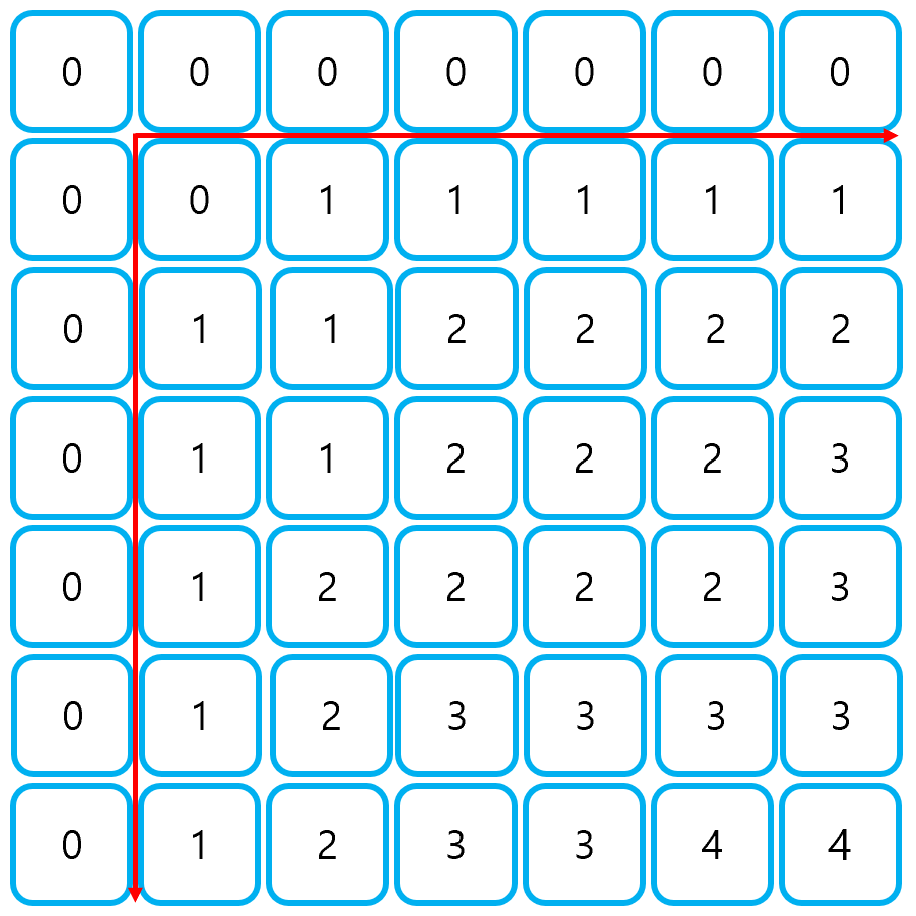
참고로, D[i][j] = D[i-1][j-1] + 1와 D[i][j] = max(D[i-1][j], D[i][j-1])의 두 점화식이 일괄적으로 적용되려면(인덱스 에러를 방지하려면), 테이블의 첫 행과 첫 열에 zero-padding을 해주어야 한다.
import sys
input = sys.stdin.readline
# 문자열을 입력받으면 개행 문자가 포함되므로, 이를 제거하기 위해 strip() 사용
A = input().strip()
B = input().strip()
D = [[0 for col in range(len(B) + 1)] for row in range(len(A) + 1)] # zero padding
for i in range(1, len(A) + 1):
for j in range(1, len(B) + 1):
# A와 B의 인덱스는 0부터 시작이므로 i-1, j-1을 사용해야 함
if A[i - 1] == B[j - 1]: # 행과 열의 문자가 같은 경우
D[i][j] = D[i-1][j-1] + 1
else: # 행과 열의 문자가 다른 경우
D[i][j] = max(D[i][j-1], D[i-1][j])
row, col = len(A), len(B) # 테이블의 마지막 부분
LCS = [] # LCS의 원소 저장
while row > 0 and col > 0: # row나 col 중 하나라도 0이랑 같아지면 안 됨 (zero padding 된 곳이기 때문)
if A[row - 1] == B[col - 1]: # 행과 열의 문자가 같은 경우
LCS.append(A[row - 1]) # 값을 저장
row -= 1 # 대각선 왼쪽으로 이동
col -= 1
else: # 행과 열의 문자가 다른 경우
if D[row - 1][col] > D[row][col - 1]:
row -= 1
else:
col -= 1
print(D[len(A)][len(B)]) # LCS의 길이 출력
LCS.reverse()
print(''.join(LCS)) # 역순 출력2. 가장 큰 정사각형 찾기
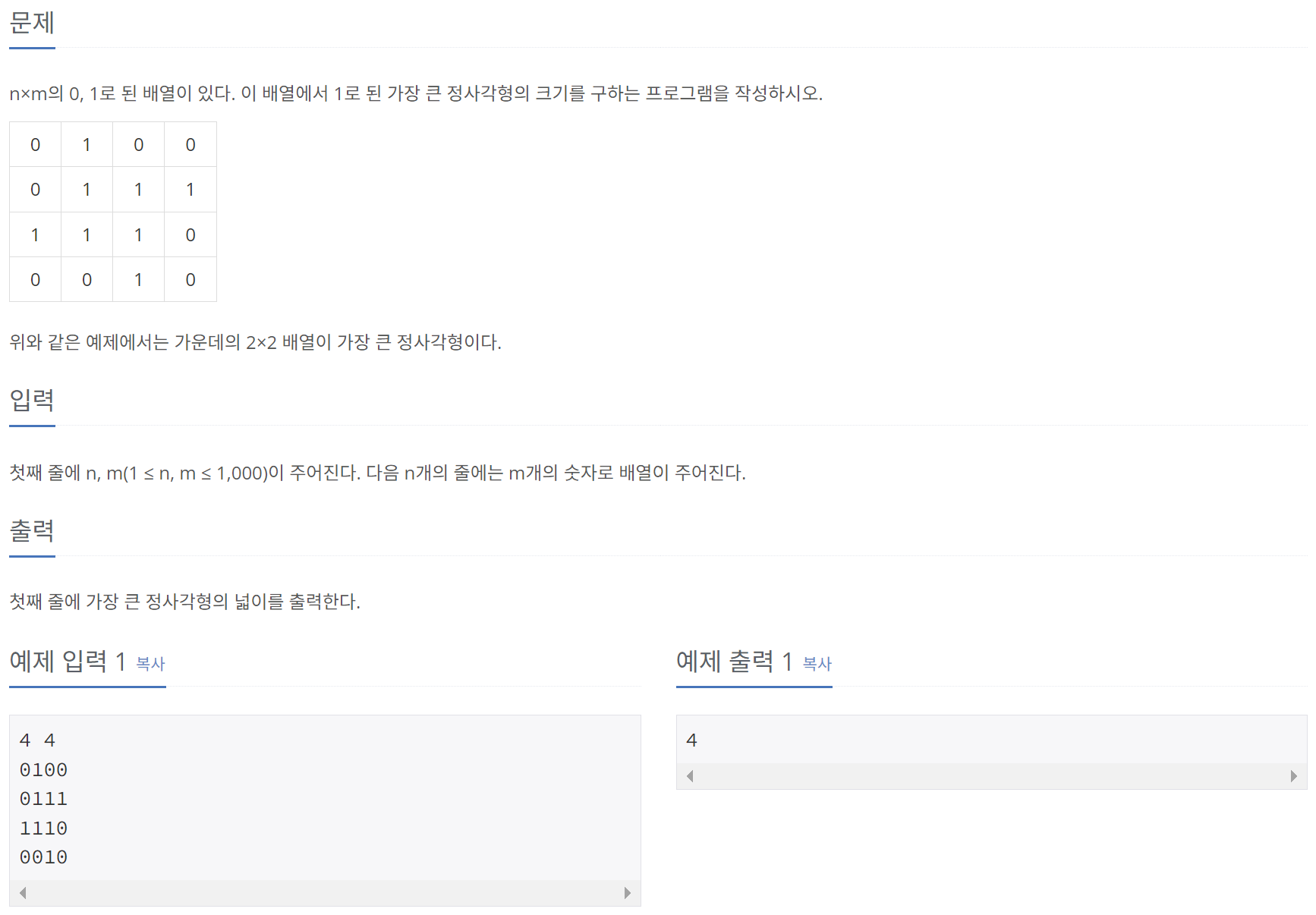
문제를 보아하니, D[i][j]를 "(0, 0)에서 (i, j) 좌표까지 그릴 수 있는 가장 큰 정사각형의 크기"로 정의하면 될 것 같다. 하지만, 이 정의에는 수정해야 할 부분이 있다.
위의 정의대로 문제를 풀어보면, 부분 문제가 여전히 어려운 문제라는 사실을 알 수 있을 것이다. 바로 이러한 문제가 지난 포스팅에서 설명했던, "최적 값의 위치를 알 수 없는 경우"로 분류하여 풀이해야 하는 문제인 것이다.
따라서, D[i][j]를 "(i, j) 좌표를 정사각형의 우하단 끝점으로 둔 상태에서 그릴 수 있는 가장 큰 정사각형의 크기"로 재정의하겠다. 그런데 생각해보면, 정사각형의 크기는 한 변의 길이를 제곱하여 구해지는 값이므로, 정사각형의 크기 대신 한 변의 길이만 저장해도 충분할 것 같다. 그러므로, 최종적인 DP 테이블의 정의는 "(i, j) 좌표를 정사각형의 우하단 끝점으로 둔 상태에서 그릴 수 있는 가장 큰 정사각형의 한 변의 길이"가 된다.
이제 점화식을 정의해보자. 우리가 고려해야 하는 상황은 아래의 두 가지 경우이다.
- 현재 인덱스가 원래 배열에서 0의 위치인 경우
- 현재 인덱스가 원래 배열에서 1의 위치인 경우
전자의 경우, 현재 인덱스를 끝점으로 하는 정사각형을 만들 수 없으므로, 0이 될 것이다. 반면 후자의 경우는 점화식을 바로 도출하는 일이 쉽지 않기 때문에, 우선 직접 그려보기로 한다.
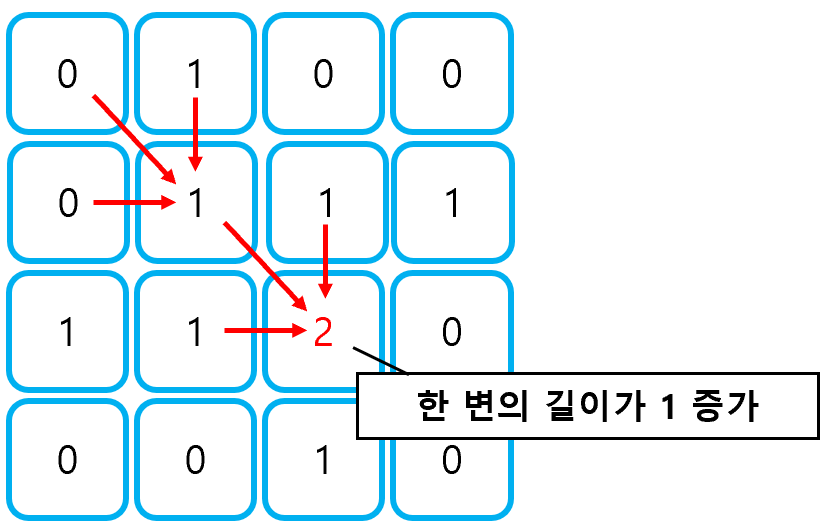
DP 테이블의 값은 왼쪽 대각선, 위, 왼쪽 중 최소 값에 1을 더한 수로 계산된다. 즉, 원래 배열에서 왼쪽 대각선, 위, 왼쪽 모두 1일 때에만, 정사각형의 한 변의 길이가 증가하는 것이다. 이를 점화식으로 나타내면 아래와 같다.
if (원래 배열에서 0의 위치) D[i][j] = 0
if (원래 배열에서 1의 위치) D[i][j] = min(D[i-1][j], D[i][j-1], D[i-1][j-1]) + 1이제 점화식을 이용하여 문제를 풀어보자.
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
lst = []
D = [[0 for col in range(m + 1)] for row in range(n + 1)] # zero padding
for i in range(n):
lst.append(list(map(int, list(input().strip())))) # 띄어쓰기 없이 주어지는 입력을 정수형 배열로 변환
length = 0 # 가장 큰 정사각형의 한 변의 길이
for i in range(1, n + 1):
for j in range(1, m + 1):
if lst[i - 1][j - 1] == 1: # lst의 원소가 1인 경우(lst의 인덱스는 0부터 시작하므로, i-1과 j-1 사용)
D[i][j] = min(D[i-1][j], D[i][j-1], D[i-1][j-1]) + 1
length = max(length, D[i][j]) # length 값 업데이트
else:# lst의 원소가 0인 경우, D[i][j]는 0이 됨
D[i][j] = 0
print(length ** 2) # 정사각형의 크기(넓이) 출력3. 빌딩 순서 구하기
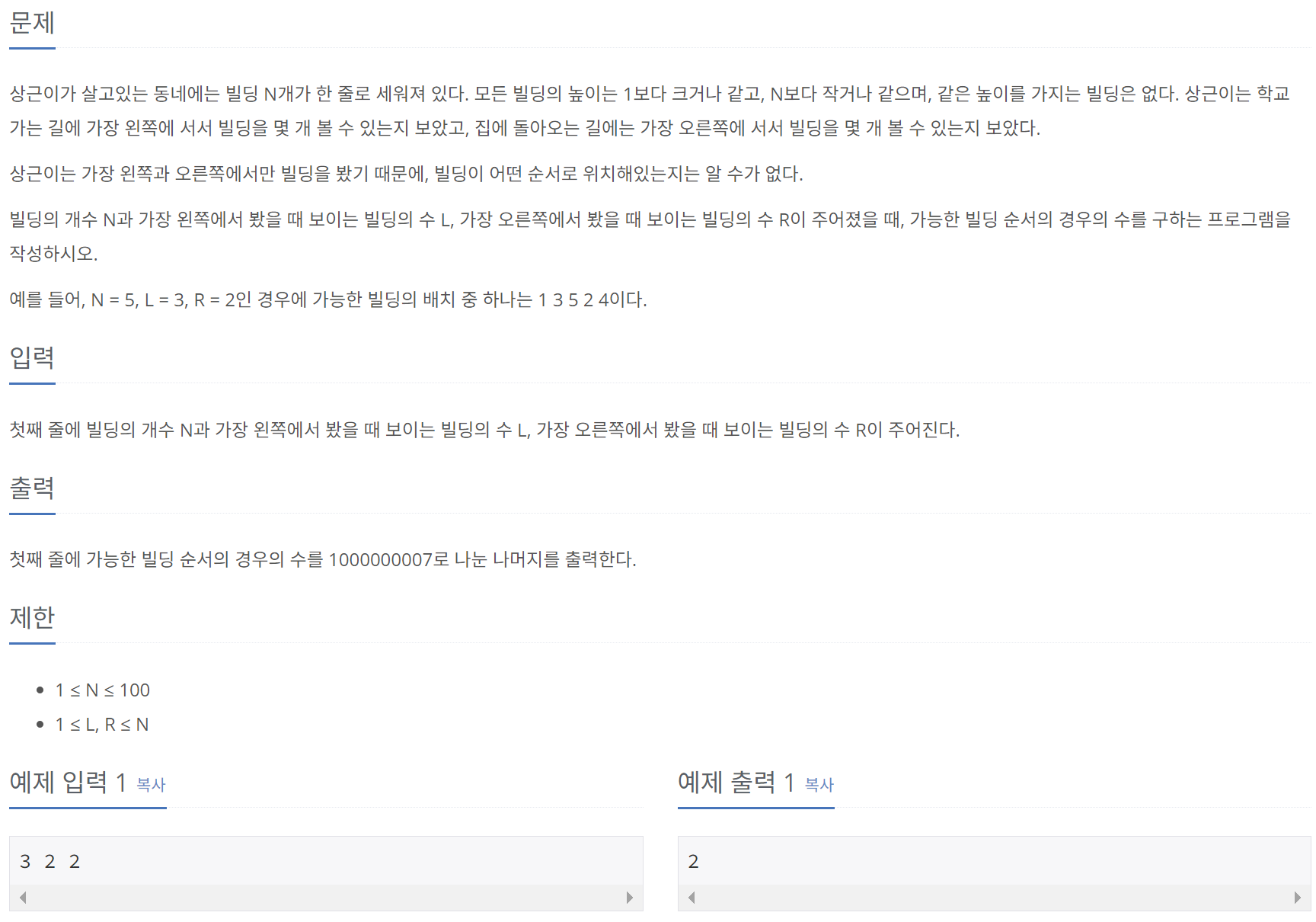
점화식을 정의하기 매우 까다로운 문제이다. 일단 D[N][L][R]을 "N개의 빌딩이 있고 왼쪽에서 L개, 오른쪽에서 R개가 보일 때 가능한 빌딩 순서의 수"로 정의할 수 있을 것이다. 여기서 중요한 것은 왼쪽(또는 오른쪽) 빌딩의 개수가 하나 증가하려면, 가장 낮은 빌딩을 맨 왼쪽(또는 오른쪽)에 배치해야 한다는 것이다.
점화식을 정의하기 어려운 문제는 N = 1부터 차근차근 늘려가는 방식으로 점화식을 도출하는 것이 좋다. 먼저 빌딩이 하나인 경우, 빌딩 순서의 수도 1개이므로, D[1][1][1] = 1로 초기화된다. N이 2가 되면, 가장 낮은 빌딩을 배치하는 경우는 아래의 두 가지로 구분된다.
- D[1][1][1]에서 가장 낮은 빌딩이 왼쪽에 배치되는 경우
- D[1][1][1]에서 가장 낮은 빌딩이 오른쪽에 배치되는 경우
즉, D[2][2][1] = D[1][1][1], D[2][1][2] = D[1][1][1]이 된다.
N이 3이상이 되면, 가장 낮은 빌딩이 중간에 배치되는 경우도 고려해주어야 한다. 따라서, N이 3인 경우, 가장 낮은 빌딩을 배치하는 경우는 아래의 3가지로 구분된다.
- 가장 낮은 빌딩이 맨 왼쪽에 배치되는 경우
- 가장 낮은 빌딩이 맨 오른쪽에 배치되는 경우
- 가장 낮은 빌딩이 가운데에 배치되는 경우
여기서 주의해야 할 것은, 가장 낮은 빌딩이 가운데에 배치되는 경우에 대해서는 빌딩의 수가 N개일 때, (N-2)개의 경우의 수가 존재하므로 (N-2)를 곱해주어야 한다는 것이다. 위 내용을 일반화하여 점화식을 작성해보면, D[N][L][R] = D[N-1][L-1][R] + D[N-1][L][R-1] + D[N-1][L][R] * (N-2)가 된다. 이는 가장 낮은 빌딩을 배치하는 위 3가지 경우를 수식으로 나타낸 결과이다. 이제 이 점화식을 이용하여 문제를 풀어보자.
import sys
input = sys.stdin.readline
N, L, R = map(int, input().split())
D = [[[0 for k in range(R + 1)] for j in range(L + 1)] for i in range(N + 1)]
D[1][1][1] = 1 # 빌딩이 하나인 경우, 빌딩 순서의 수도 1개임
for i in range(2, N + 1):
for j in range(1, L + 1): # L과 R의 최소값은 1이므로, 1부터 시작
for k in range(1, R + 1):
# 가장 낮은 빌딩을 맨 왼쪽에 배치 + 가장 낮은 빌딩을 맨 오른쪽에 배치 + 가장 낮은 빌딩을 가운데에 배치
D[i][j][k] = (D[i - 1][j - 1][k] + D[i - 1][j][k - 1] + D[i - 1][j][k] * (i - 2)) % 1000000007
print(D[N][L][R])4. DDR을 해보자
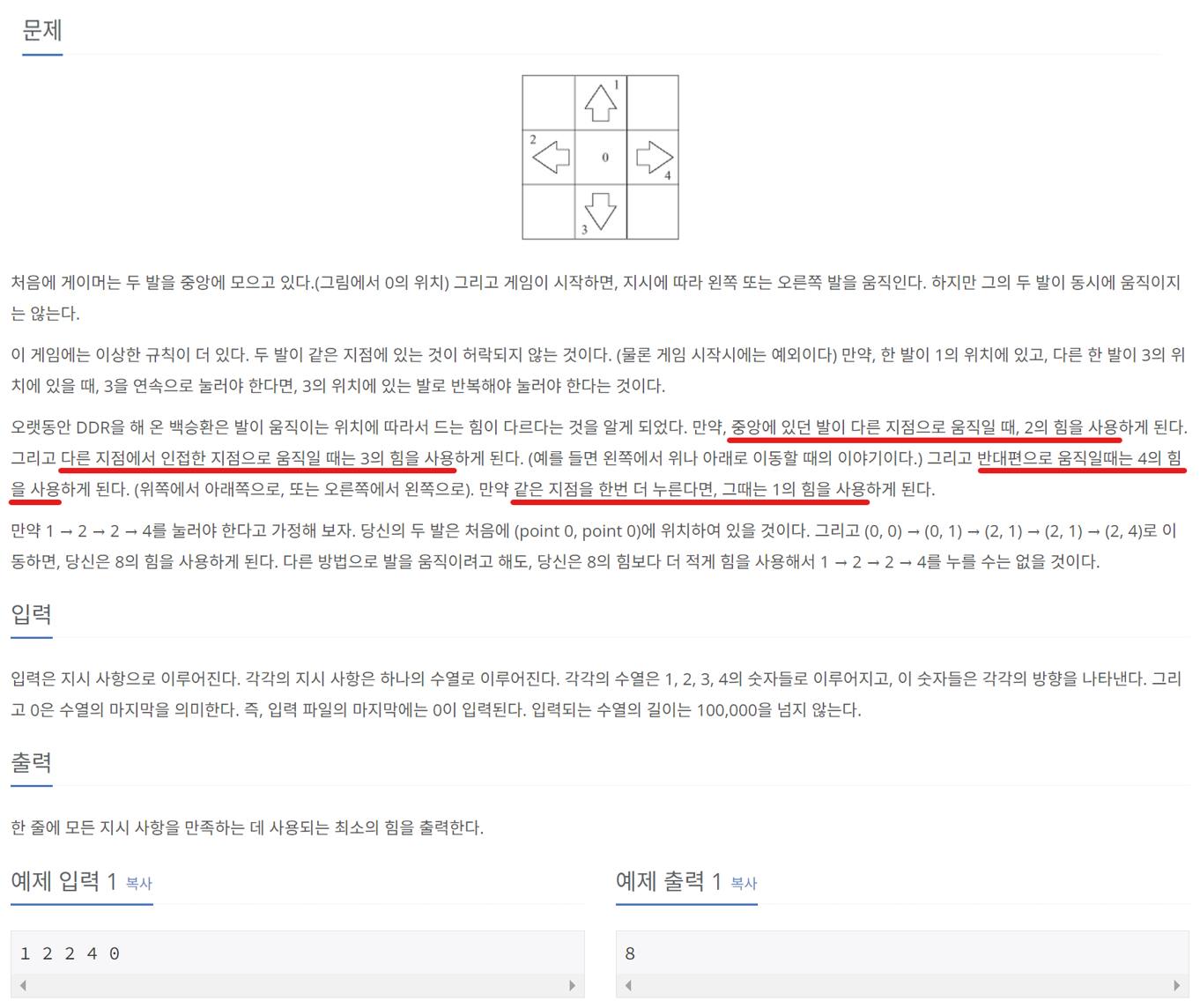
이 문제를 보고 바로 DP를 연상할 수 있다면, DP 문제 풀이를 위한 능력이 충분히 배양되었다고 생각해도 될 것 같다. 비록 점화식을 정의하기는 다소 까다로운 문제이지만, 적어도 이전 단계까지의 최소 힘을 이용해 현재 단계의 최소 힘을 구해야 한다는 것 정도는 충분히 생각해낼 수 있기 때문이다.
같은 지점, 인접 지점, 반대 지점을 누를 때에 필요한 힘이 다르기 때문에, 어떤 발이 이전에 어디를 누르고 있었는지를 저장해야 할 필요가 있다. 따라서, D[N][L][R]을 "N개의 지시를 수행한 후 왼발의 위치가 N, 오른발의 위치가 R일 때의 최소 힘"으로 정의하기로 한다.
DP 테이블을 위와 같이 정의함으로써 이전 단계까지의 최소 힘을 이용해 현재 단게의 최소 힘을 구하는 것이 가능해졌다. 예를 들어 오른발이 R’의 자리에 있다가 R로 이동한 경우, D[N][L][R] = D[N-1][L][R’] + mv[R’][R]이 될 것이다(오른발로 누를 때, 더 적은 힘이 든다고 가정). 반대로, 왼발이 L’의 자리에 있다가 L로 이동한 경우, D[N][L][R] = D[N-1][L’][R] + mv[L’][L]이 될 것이다(왼발로 누를 때, 더 적은 힘이 든다고 가정). 참고로, 여기서 mv[i][j]는 i에서 j로 이동하는 데 필요한 힘으로 정의된다.
당연히 실제로 계산을 할 때에는, 왼발과 오른발 중 어떤 발로 누르는 것이 유리할지도 고려해주어야 한다. 즉, 왼발로 누르는 경우와 오른발로 누르는 경우를 구분하여 최소 값을 구해야 한다.
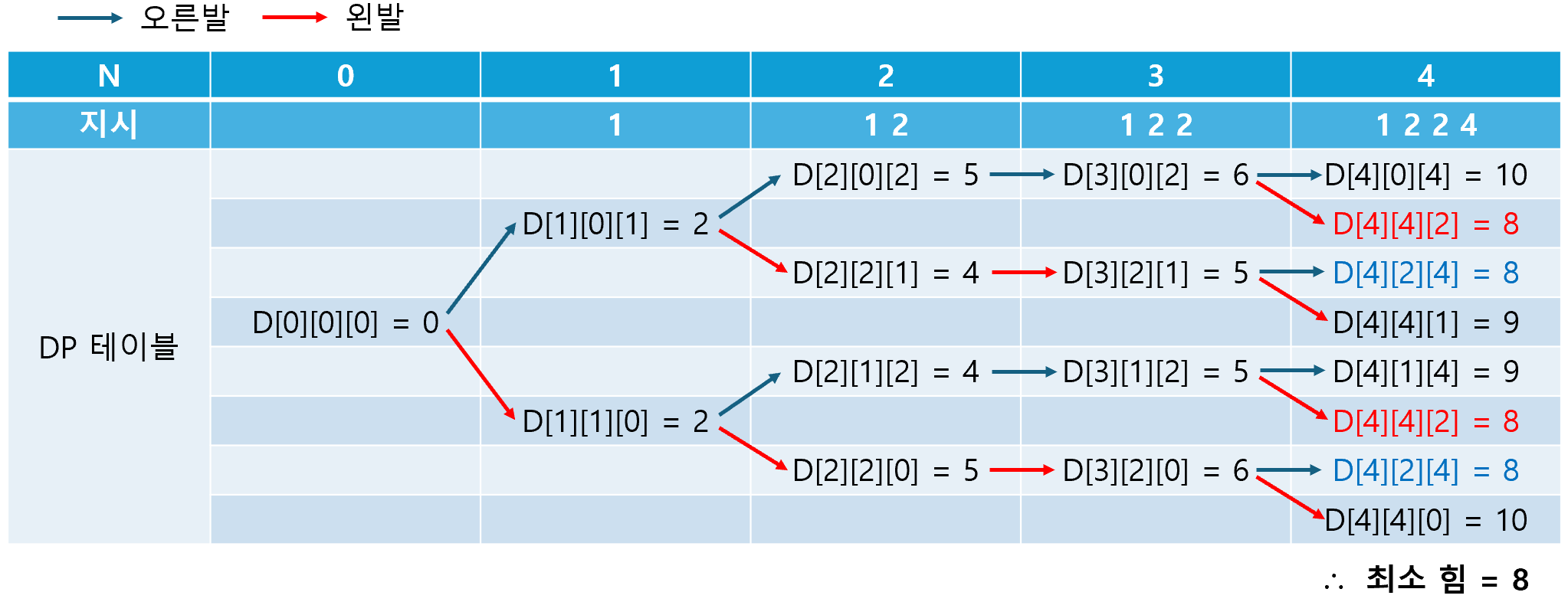
한 가지 주의해야 할 것은 동일한 N, L, R에 대해서도, 여러 개의 값이 계산될 수 있다는 것이다. 위에 빨간색과 파란색으로 표시된 부분이 동일한 값인데, 이는 우연히 같은 값일 뿐 원래는 다를 수도 있는 값이다. 따라서 N, L, R에 대하여 3중 for문을 돌면서, 최소가 되는 값으로 업데이트하는 과정이 필요하다. 이제 문제를 풀어보자.
import sys
input = sys.stdin.readline
lst = list(map(int, input().split()))
N = len(lst)
# 최소 값을 찾는 문제이므로, maxsize로 초기화
D = [[[sys.maxsize for k in range(5)] for j in range(5)] for i in range(N + 1)]
mv = [[0, 2, 2, 2, 2], # 중앙에 있던 발을 다른 지점으로 움직이는 경우
[0, 1, 3, 4, 3], # 1번에 있던 발을 인접 지점 또는 반대 지점으로 움직이는 경우
[0, 3, 1, 3, 4], # 2번에 있던 발을 인접 지점 또는 반대 지점으로 움직이는 경우
[0, 4, 3, 1, 3], # 3번에 있던 발을 인접 지점 또는 반대 지점으로 움직이는 경우
[0, 3, 4, 3, 1], # 4번에 있던 발을 인접 지점 또는 반대 지점으로 움직이는 경우
]
D[0][0][0] = 0 # 아무런 지시가 없었으므로 필요한 힘도 0이 됨
n = 0 # 지시의 길이
for num in lst: # num은 지시의 각 숫자를 의미
if num == 0: # 지시가 끝났음을 알리는 Flag
break
n += 1 # 지시의 길이 1 증가
# 오른발로 num을 누르는 경우
for i in range(5): # 왼발이 0, 1, 2, 3, 4에 위치하는 모든 경우를 고려
if num == i:
continue # 이미 왼발이 num에 있다면 오른발로 누르는 것이 불가(두 발이 같은 자리에 올 수 없음)
for j in range(5): # 오른발을 0, 1, 2, 3, 4에서 num으로 옮길 때 필요한 최소 힘
D[n][i][num] = min(D[n - 1][i][j] + mv[j][num], D[n][i][num]) # 왼발은 i에, 오른발은 num에 위치
# 왼발로 num을 누르는 경우
for i in range(5): # 오른발이 0, 1, 2, 3, 4에 위치하는 모든 경우를 고려
if num == i:
continue # 이미 오른발이 num에 있다면 왼발로 누르는 것이 불가(두 발이 같은 자리에 올 수 없음)
for j in range(5): # 왼발을 0, 1, 2, 3, 4에서 num으로 옮길 때 필요한 최소 힘
D[n][num][i] = min(D[n - 1][j][i] + mv[j][num], D[n][num][i])
result = sys.maxsize # 최대 값을 찾을 때 result를 0으로 초기화하듯, 최소 값을 찾을 때에는 result를 maxsize로 초기화함
for i in range(5):
for j in range(5):
result = min(result, D[n][i][j]) # 지시의 길이가 N인 원소 중 최소 값
print(result)