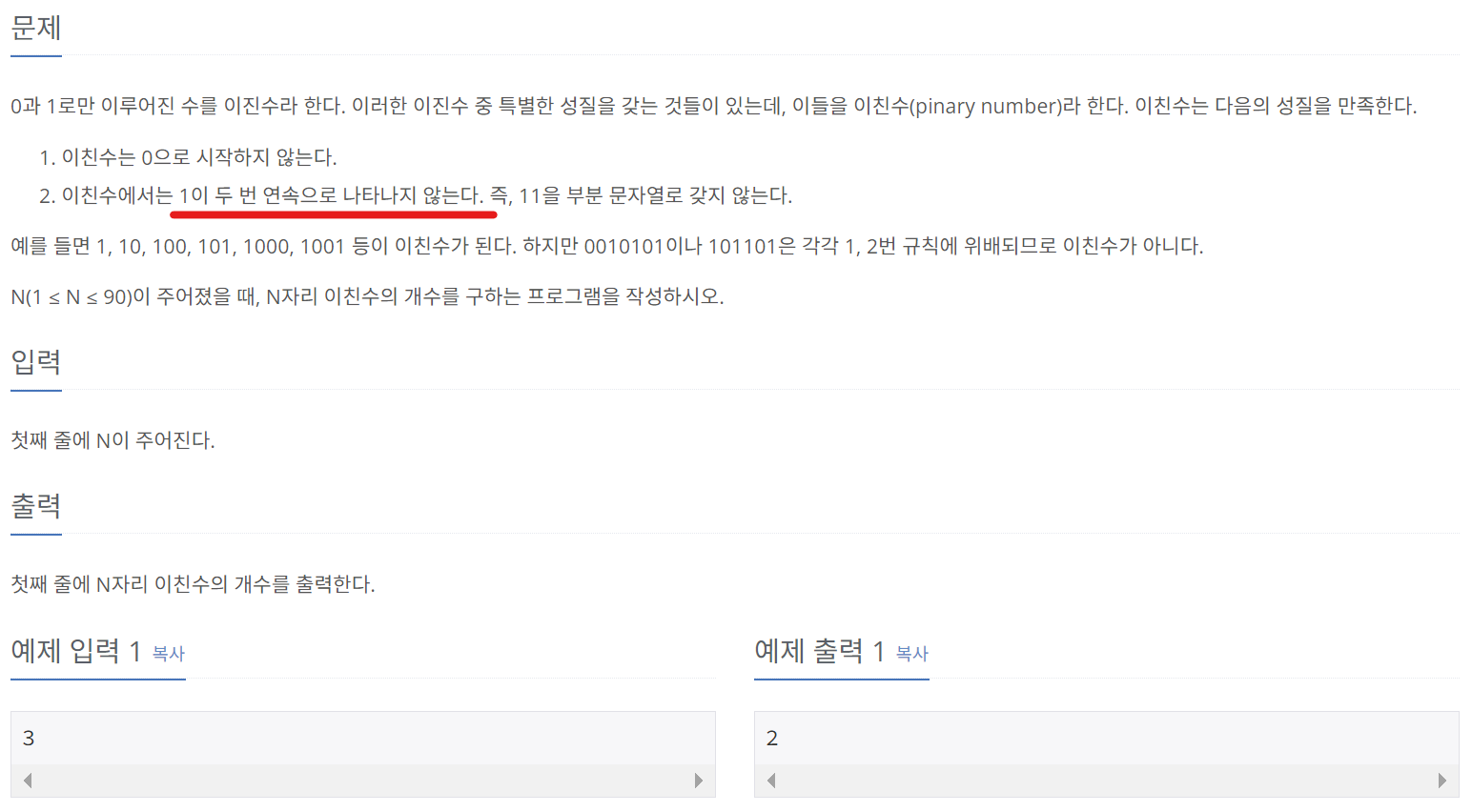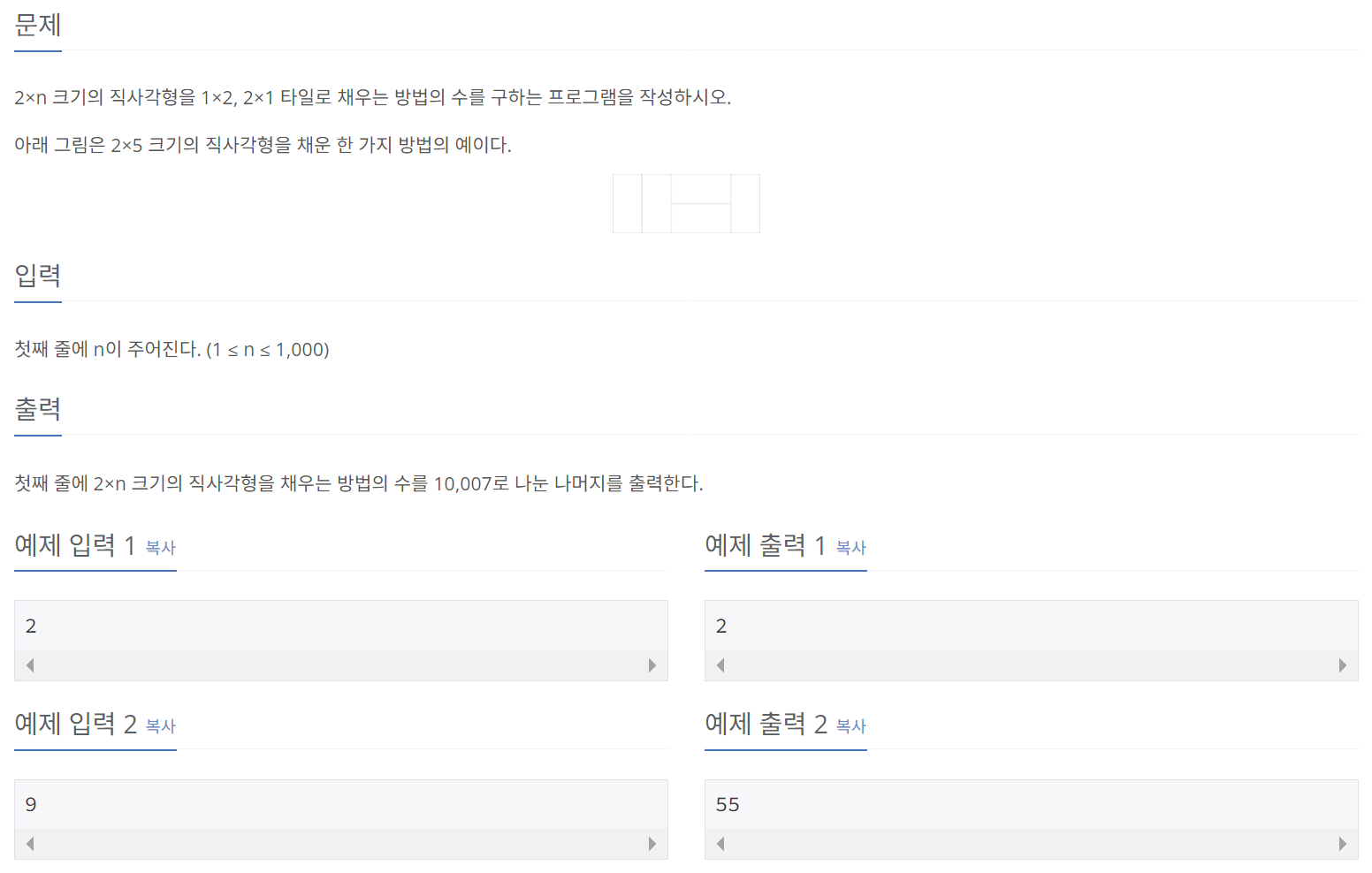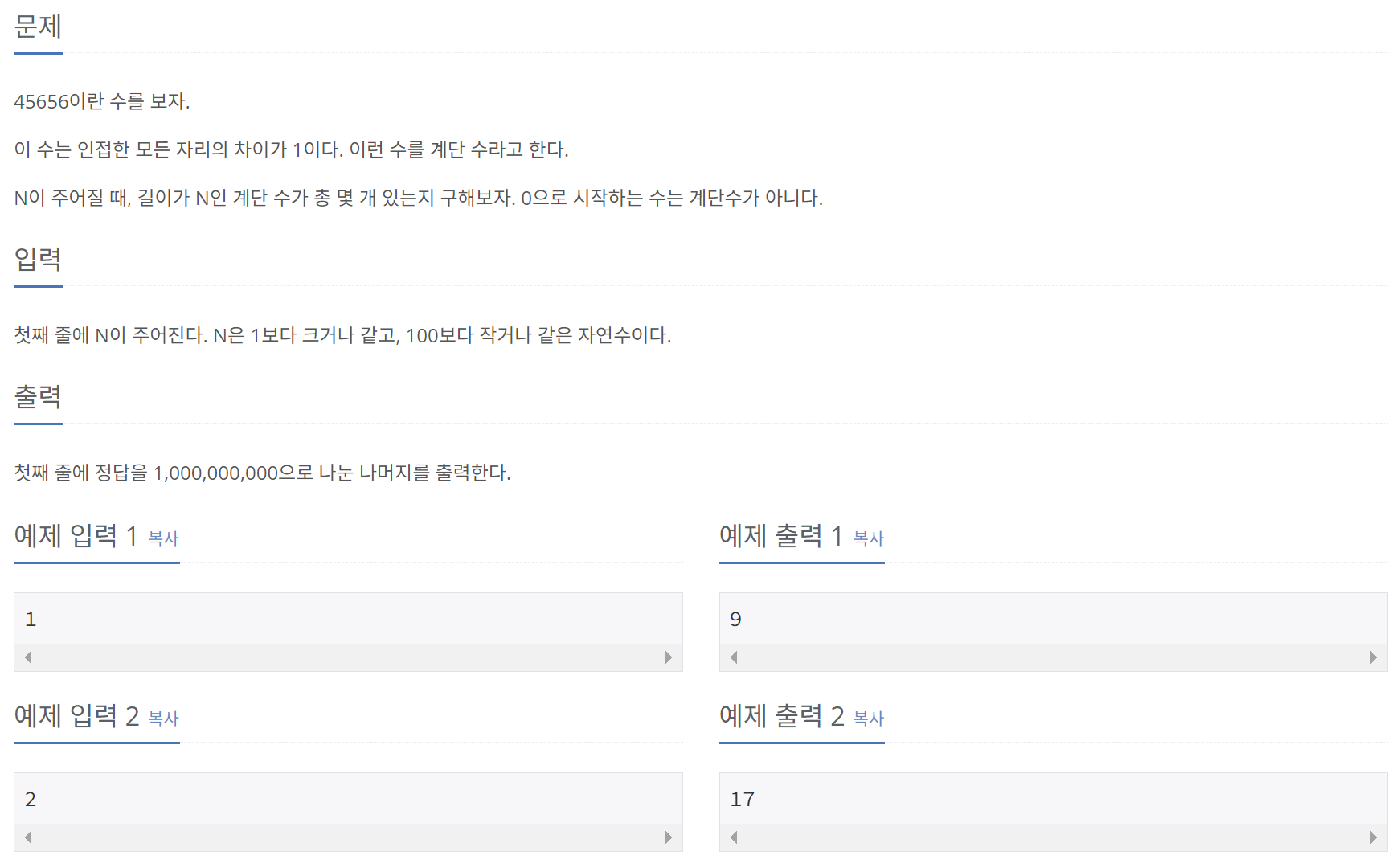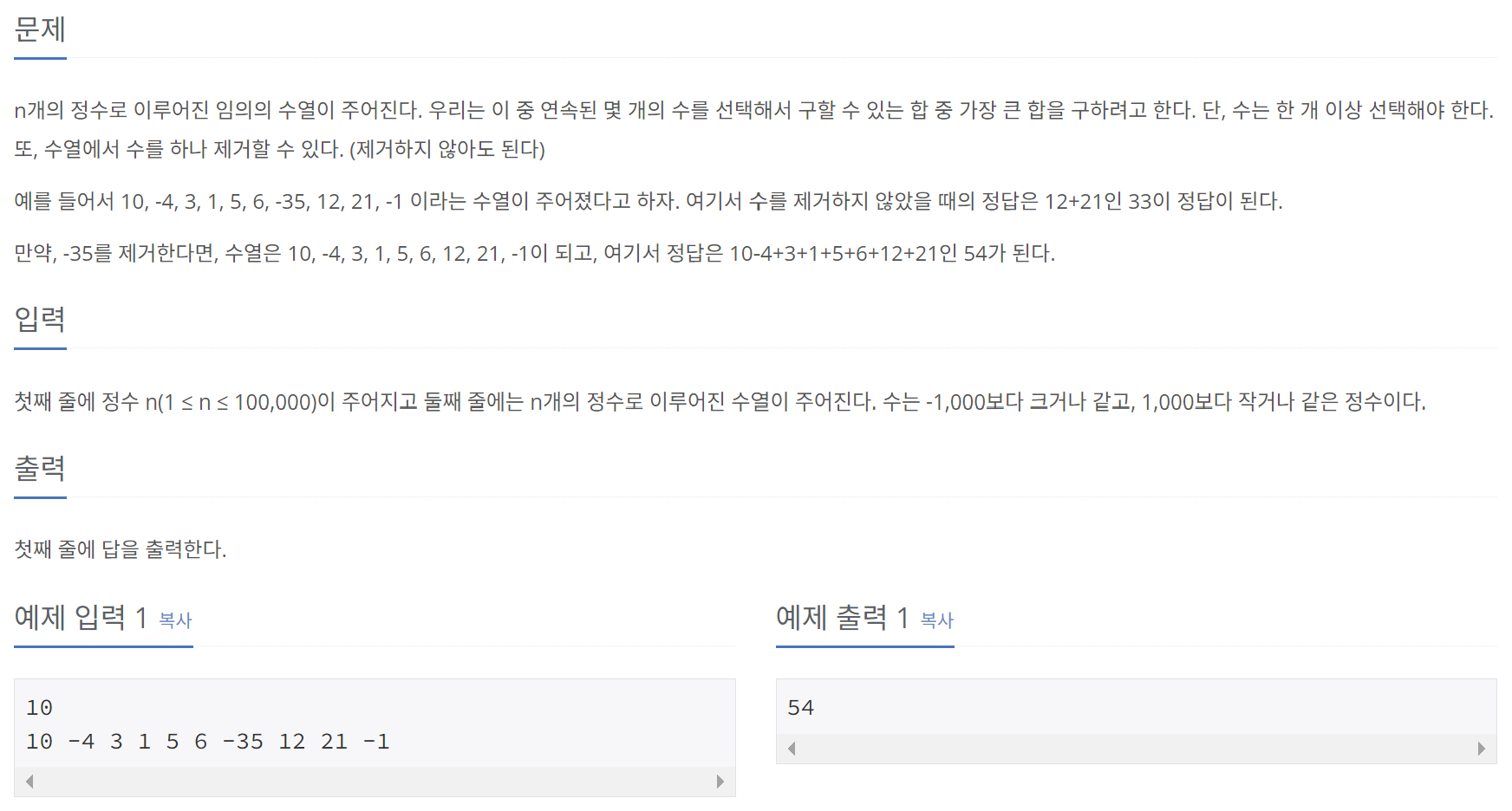
1. 이친수 구하기
1) 일반적인 풀이
1이 두 번 연속으로 나타나지 않는다는 조건에서 DP를 연상할 수 있어야 한다. 그 이유는 (N-1) 자리 이친수 중 0으로 끝나는 수의 개수와 1로 끝나는 수의 개수를 알고 있다면, 그 숫자 뒤에 0 또는 1을 붙여 이진수의 개수를 쉽게 구할 수 있기 때문이다.
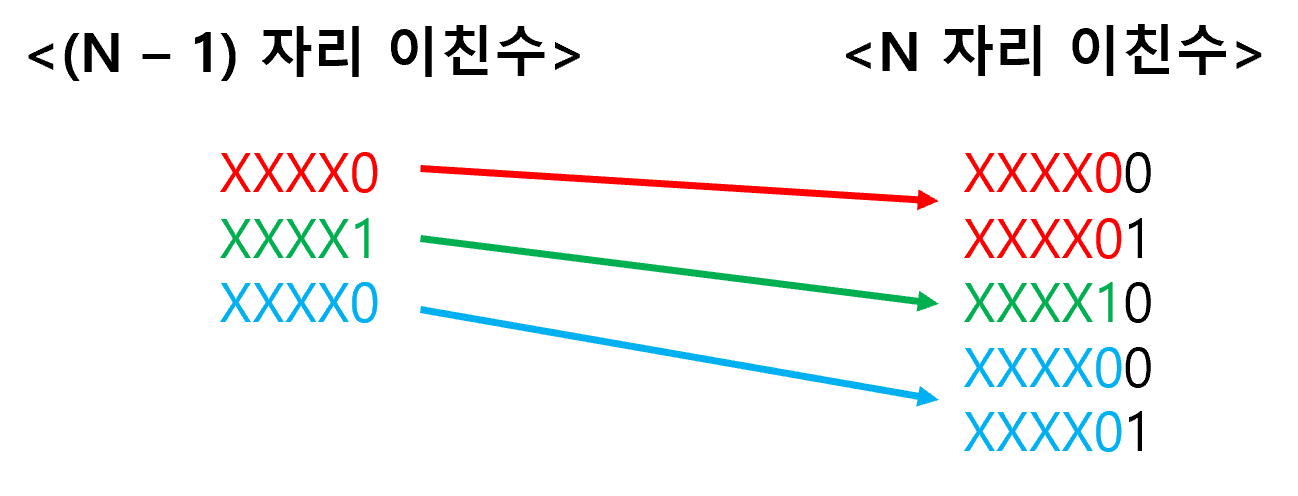
즉, (N-1) 자리 이친수 중 0으로 끝나는 수의 개수를 D[N-1][0], 1로 끝나는 수의 개수를 D[N-1][1]이라고 하면, 점화식은 D[N][0] + D[N][1] = D[N-1][0] + D[N-1][1] + D[N-1][0]이 된다. 이 점화식의 의미는 N자리 이친수 중 0으로 끝나는 수의 개수는 (N-1) 자리의 모든 이친수의 개수(모든 이친수에 0을 붙인 개수)와 같고, 1로 끝나는 수의 개수는 (N-1) 자리의 이친수 중 0으로 끝나는 수의 개수와 같다는 의미가 된다.

import sys
input = sys.stdin.readline
N = int(input())
D = [[0 for col in range(2)] for row in range(N + 1)]
# 한자리 이친수는 1밖에 없음
D[1][0] = 0
D[1][1] = 1
for n in range(2, N + 1):
# N자리 이친수 중 0으로 끝나는 수의 개수는 (N-1) 자리의 모든 이친수의 개수와 같음
D[n][0] = D[n - 1][0] + D[n - 1][1]
# N자리 이친수 중 1로 끝나는 수의 개수는 (N-1) 자리의 이친수 중 0으로 끝나는 수의 개수와
D[n][1] = D[n - 1][0]
print(D[N][0] + D[N][1])2) 피보나치 수열을 이용한 풀이
사실 위 문제를 좀 더 쉽게 풀이할 수 있는 방법이 있는데, 바로 피보나치 수열을 이용하는 것이다. n = 1부터 차례차례 이친수의 개수를 구해보면, 이친수의 개수가 피보나치 수열을 따른다는 것을 발견할 수 있다.
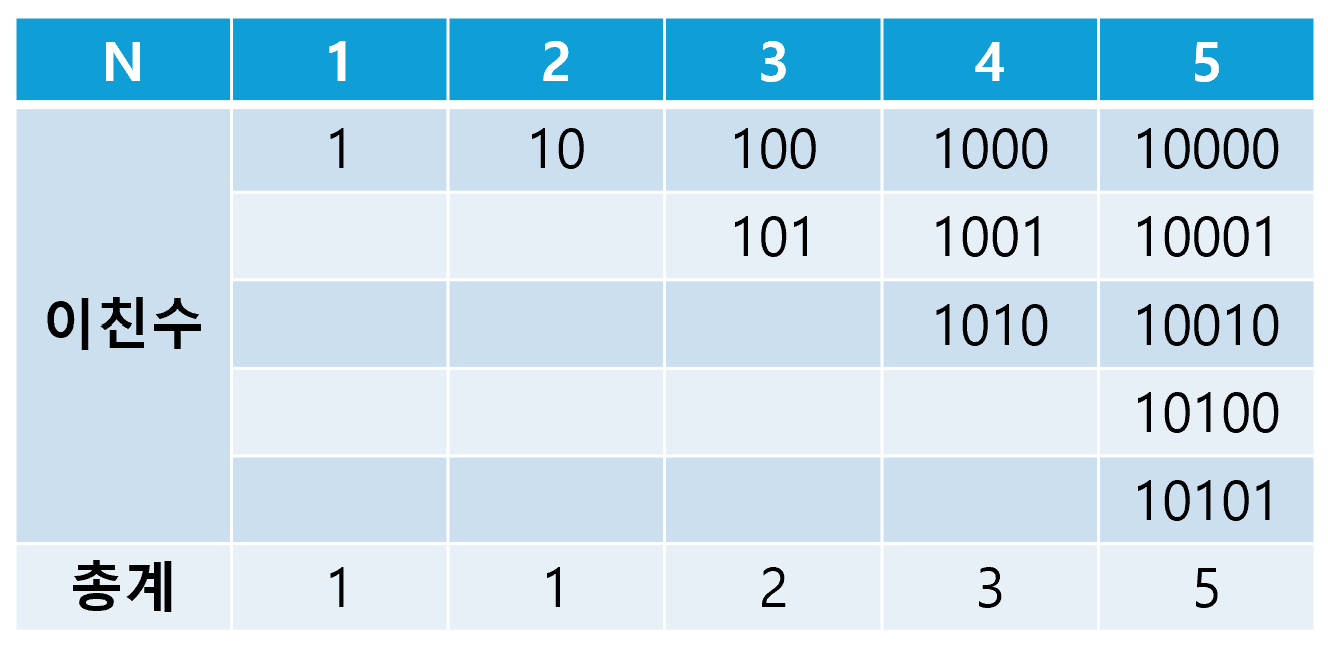
그래서 피보나치 수열 문제 풀이와 동일한 방식의 풀이도 가능하다.
import sys
input = sys.stdin.readline
N = int(input())
D = [0 for _ in range(N + 1)] # D[0] = 0
D[1] = 1
for i in range(2, N + 1):
D[i] = D[i-2] + D[i-1]
print(D[N])그러나, 개인적으로는 이와 같은 풀이는 별로 실용적이지 않은 것 같다. 그 이유는 위 문제에서 피보나치 수열을 연상하기 어려우며, 다른 문제에 확장할 수 있는 풀이도 아니기 때문이다. 따라서 이와 같은 풀이 방식은 최대한 지양할 것을 권장한다.
2. 2 * N 타일 채우기
언뜻 보기에도 위에서 풀이한 이친수 구하기 문제와 비슷해보인다. 그렇게 말하는 이유는 2 * N 타일을 만드는 경우의 수는 2 * (N - 1) 타일에 세로로 타일을 하나 붙이는 경우의 수와 2 * (N - 2) 타일에 가로로 타일을 두개씩 붙이는 경우의 수의 합이기 때문이다.
이 때, 주의해야 할 것은 2 * (N - 2) 타일에 세로로 타일을 두개씩 붙이는 경우는, 이미 2 * (N - 1) 타일에 세로로 타일을 하나 붙이는 경우에서 고려하고 있으므로, 계산에서 제외해야 한다는 것이다.
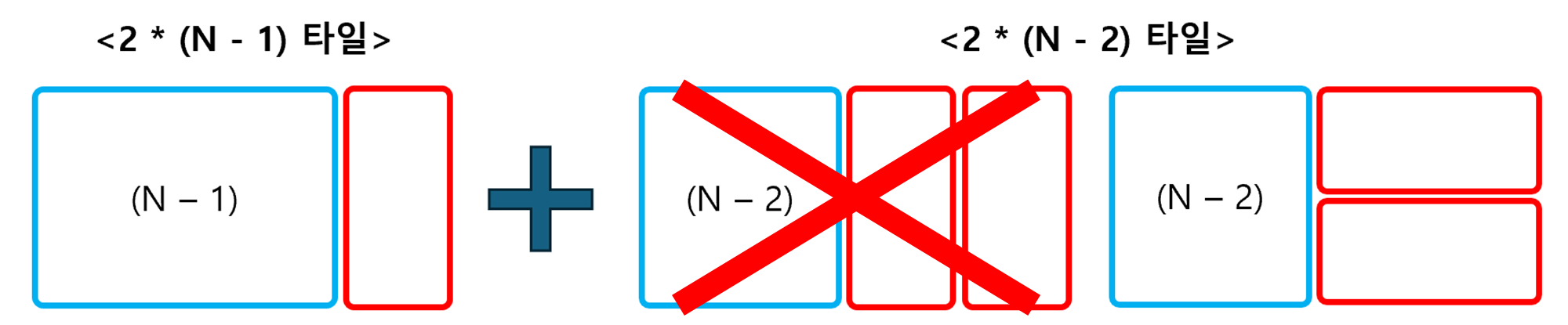
그러므로, 2 * N으로 타일을 채우는 경우의 수를 D[N]이라하면, D[N] = D[N - 1] + D[N - 2]라는 점화식을 세울 수 있게 된다. 이제 이 점화식을 바탕으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
N = int(input())
D = [0 for i in range(N + 1)]
D[1] = 1
D[2] = 2 # N이 1 이상의 값이므로, 점화식을 사용하기 위해선 최소 D[2]까지는 초기화해야 함
for n in range(3, N + 1):
D[n] = (D[n - 1] + D[n - 2]) % 10007
print(D[N])3. 계단 수 구하기
이번 문제도 비슷한 유형으로 보인다. N자리의 계단 수의 마지막 숫자가 0이려면, (N-1)번째 자리의 숫자가 반드시 1이어야 한다. 또한, 마지막 숫자가 1이려면, (N-1)번째 자리의 숫자가 0 또는 2가 되어야 하며, 마지막 숫자가 9가 되려면, (N-1)번째 자리의 숫자가 8이 되어야 한다.
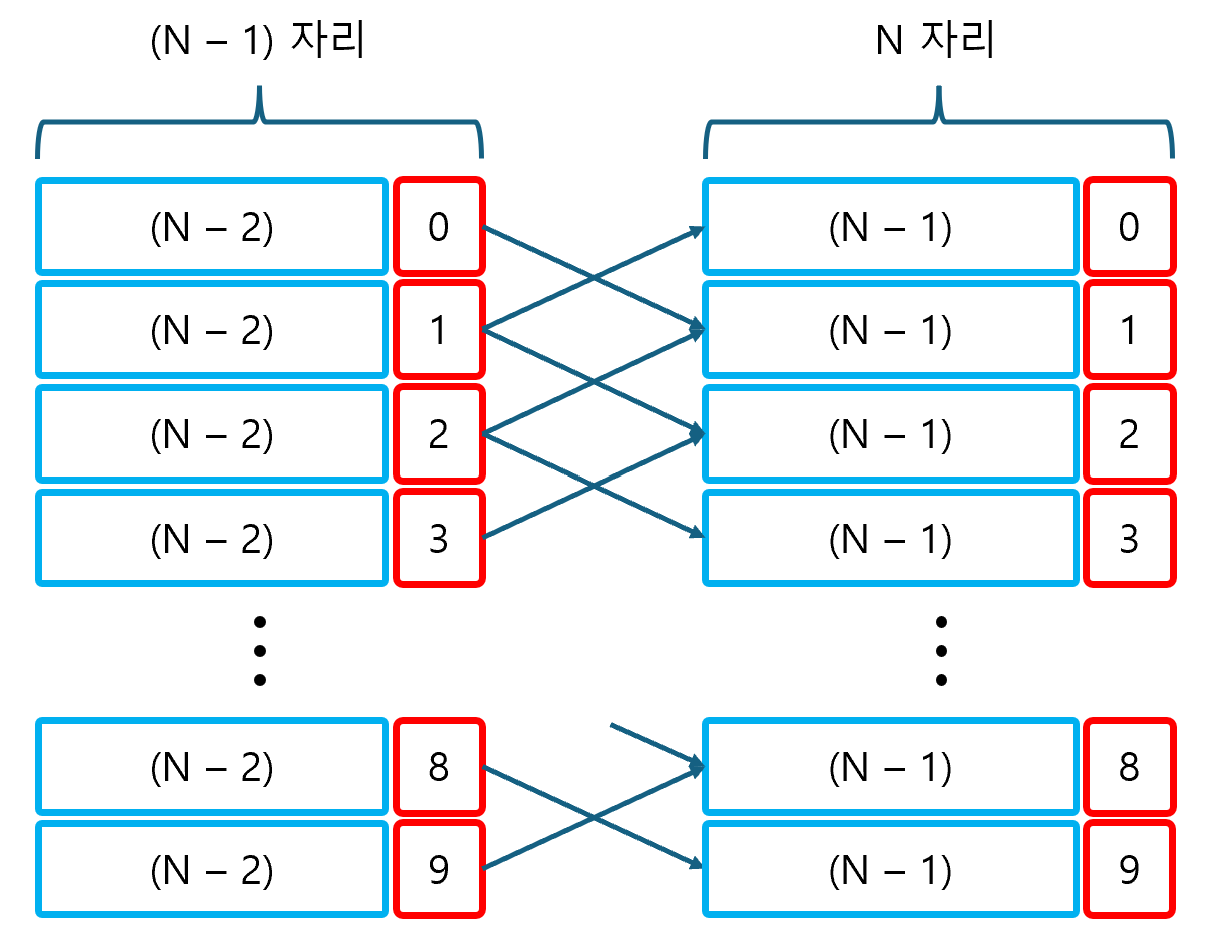
따라서, 길이가 N이고 가장자리 숫자가 E인 배열을 D[N][E]라 할 때, 아래와 같은 점화식을 작성할 수 있다.
if (E == 0) D[N][E] = D[N-1][1]
if (1 ≤ E ≤ 8) D[N][E] = D[N-1][E-1] + D[N-1][E+1]
if (E == 9) D[N][E] = D[N-1][8]이제 위 점화식을 기반으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
N = int(input())
D = [[0 for i in range(10)] for j in range(N + 1)]
for n in range(1, 10):
D[1][n] = 1 # 1의 자리 숫자는 모든 수가 계단 수임
for i in range(2, N + 1):
D[i][0] = D[i - 1][1] # E가 0인 경우
D[i][9] = D[i - 1][8] # E가 9인 경우
for j in range(1, 9): # 1 ≤ E ≤ 8인 경우
D[i][j] = D[i - 1][j - 1] + D[i - 1][j + 1]
sum = 0
for i in range(10):
sum += D[N][i] # 끝자리가 0~9인 모든 N자리 계단 수의 개수를 계산
print(sum % 1000000000)4. 연속된 정수의 합 구하기
N 자리의 수열에서 최대가 되는 연속 합을 바로 구하기는 어려운 일이다. 하지만 (N-1) 자리까지의 수열에서 최대가 되는 연속 합을 알고 있다면, N 자리의 수열에서 최대 연속 합을 구하는 일이 매우 쉬워진다. 따라서, 이 문제는 동적 계획법을 이용하여 풀이할 수 있다.
최대 연속 합은 아래의 두 가지 경우 중 하나에 해당한다.
- 원소를 제거하지 않은 상태에서의 최대 연속 합
- 원소 1개를 제거한 상태에서의 최대 연속 합
따라서, 이 두 가지 경우를 모두 구한 후 더 큰 값을 출력하면 문제가 해결된다. 편의상 전자에 사용되는 DP 테이블을 D1, 후자에 사용되는 DP 테이블을 D2라고 칭하겠다. 이제 각 경우에 대해 점화식(DP 테이블)을 정의해보자.
1) 원소를 제거하지 않은 상태에서의 최대 연속 합
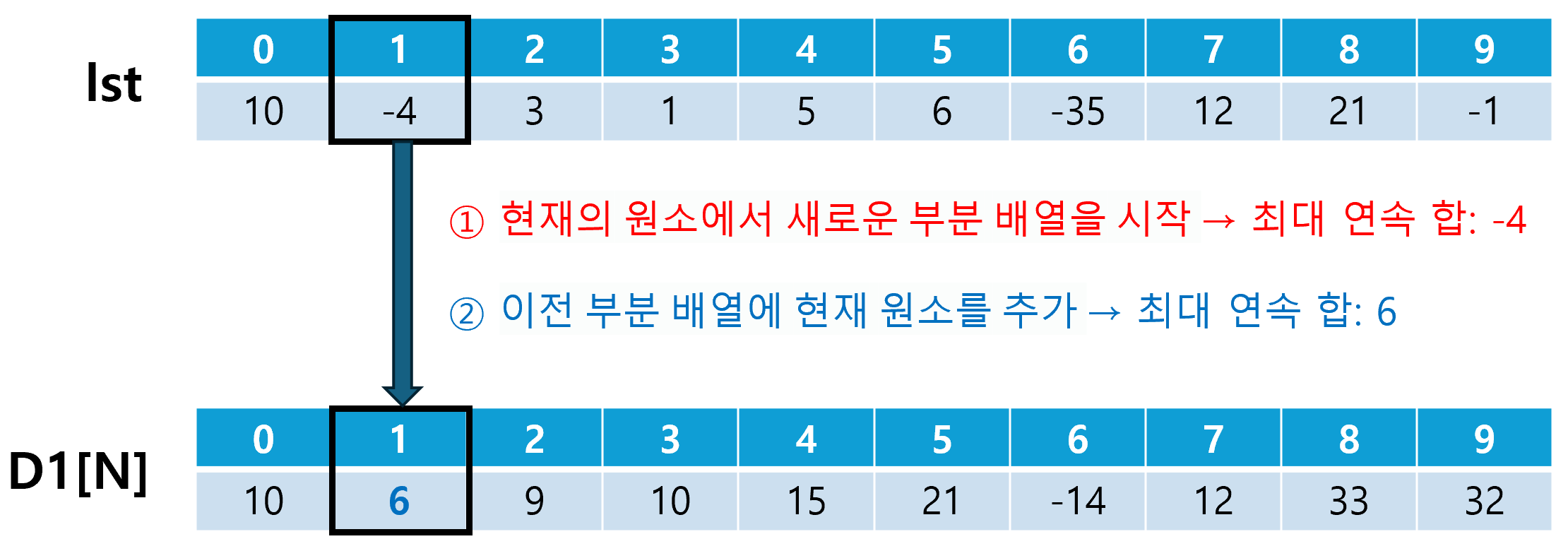
이와 같은 문제를 해결하는 알고리즘을 카데인 알고리즘이라 한다. 카데인 알고리즘은 DP를 활용한 대표적인 알고리즘으로, 주어진 배열에서 부분 합의 최대 값을 찾기 위해 사용된다. 카데인 알고리즘은 아래의 두 가지 경우 중 더 큰 값으로, 최대 부분 합을 결정한다.
- 현재의 원소에서 새로운 부분 배열을 시작하는 경우
- 이전 부분 배열에 현재 원소를 추가하는 경우
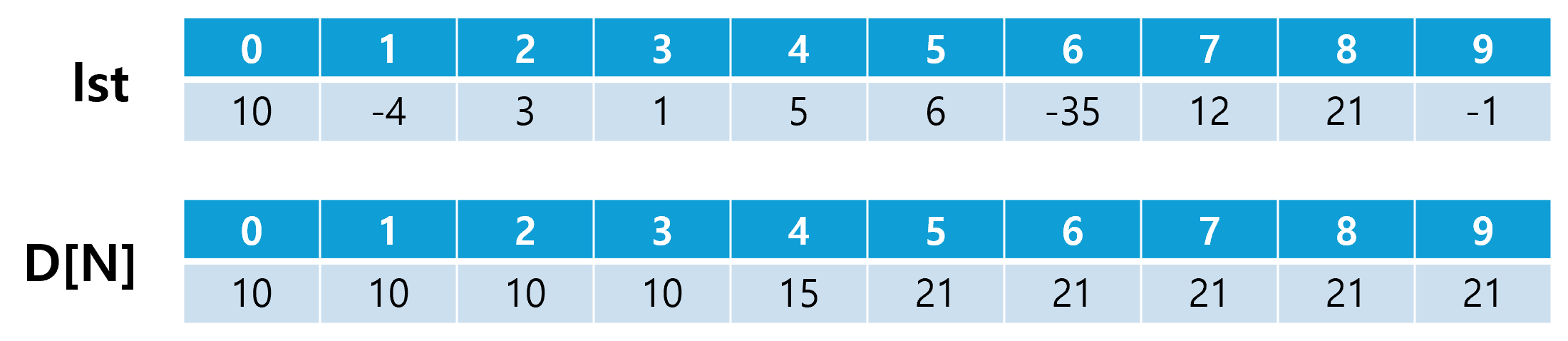
따라서, 점화식은 D1[N] = max(lst[N], D1[N-1] + lst[N])이 된다.
2) 원소 1개를 제거한 상태에서의 최대 연속 합
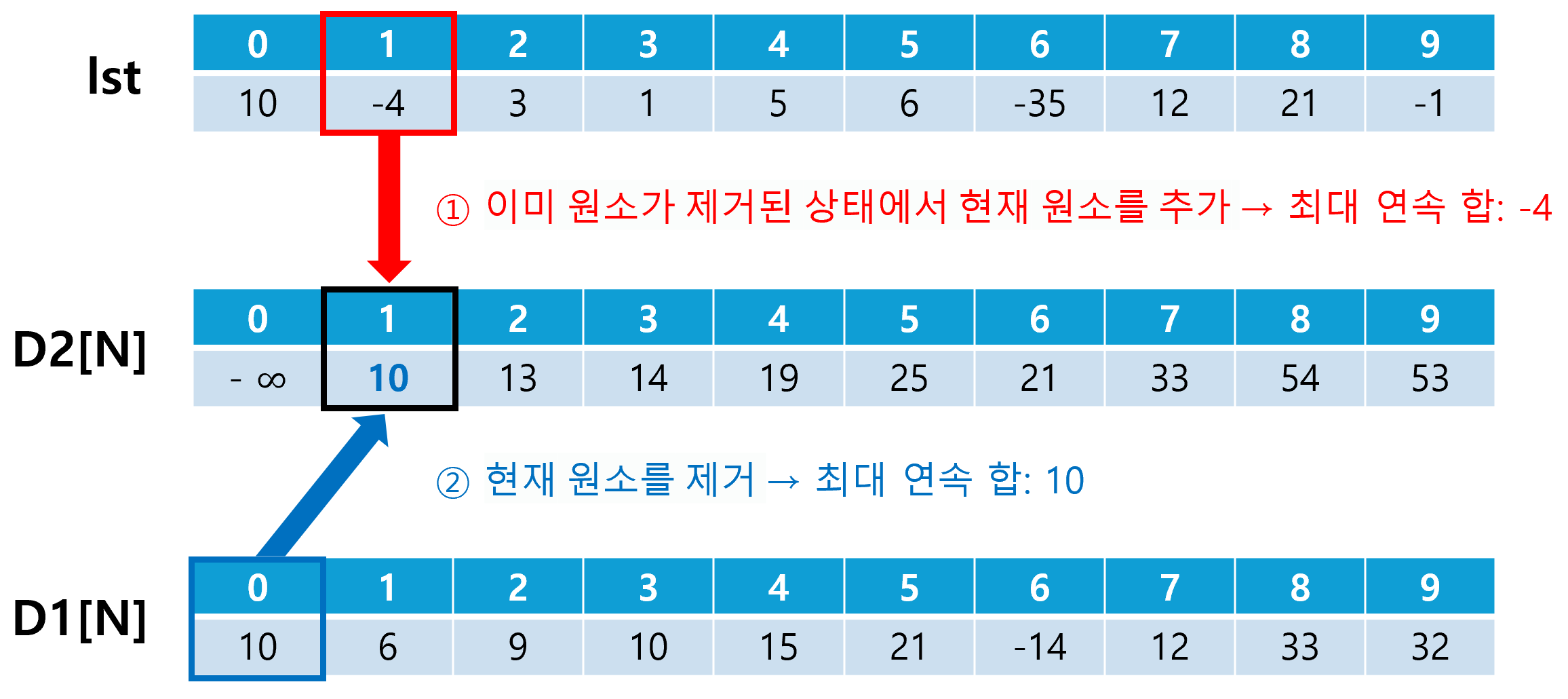
원소 1개를 제거한 상태에서의 최대 연속 합은 아래의 두 가지 경우 중 더 큰 값으로 결정된다.
- 이미 어떤 원소가 제거된 상태에서 현재 원소를 추가하는 경우
- 현재 원소를 제거하는 경우
참고로, 현재 원소를 제거하는 경우는 D1[N-1]과 같다. 따라서, 점화식은 D2[N] = max(D2[N-1] + lst[N], D1[N-1])이 된다.
3) 문제 풀이
도출한 점화식을 이용하여 문제를 풀어보자.
import sys
input = sys.stdin.readline
N = int(input())
lst = list(map(int, input().split()))
D1 = [0 for i in range(N)] # 원소를 제거하지 않은 상태에서의 최대 연속 합
D2 = [0 for i in range(N)] # 원소 1개를 제거한 상태에서의 최대 연속 합
D1[0] = lst[0] # lst의 첫번째 원소와 같음
D2[0] = - sys.maxsize # 아래 설명 참조
for i in range(1, N):
# 현재의 원소에서 새로운 부분 배열을 시작하는 경우와 이전 부분 배열에 현재 원소를 더하는 경우를 비교
D1[i] = max(lst[i], D1[i - 1] + lst[i])
# 이미 어떤 원소가 제거된 상태에서 현재 원소를 추가하는 경우와 현재 원소를 제거하는 경우를 비교
D2[i] = max(D2[i - 1] + lst[i], D1[i - 1])
result = max(max(D1), max(D2)) # D1, D2에서의 최대 값이 최대 연속 합이 됨
print(result)한 가지 주의해야 할 것은 D2[0]를 0이 아닌 -∞으로 초기화해야 한다는 것이다. 그 이유는 D2[0]가 정의되지 않는 숫자이기 때문에, 이 숫자가 연산에 사용되지 못하도록 만들기 위함이다.
간단한 예를 들면, D2[0]를 0으로 초기화했는데, lst[1]이 D1[0]보다 크다면, D2[1]은 D2[0] + lst[1] = lst[1]으로 정의될 것이다. 하지만, D2[0]가 0이라는 것은 임의로 초기화된 값일뿐 실제 값이 아니다. 당연히 이에 따라 예기치 않은 동작을 일으키게 될 것이다.
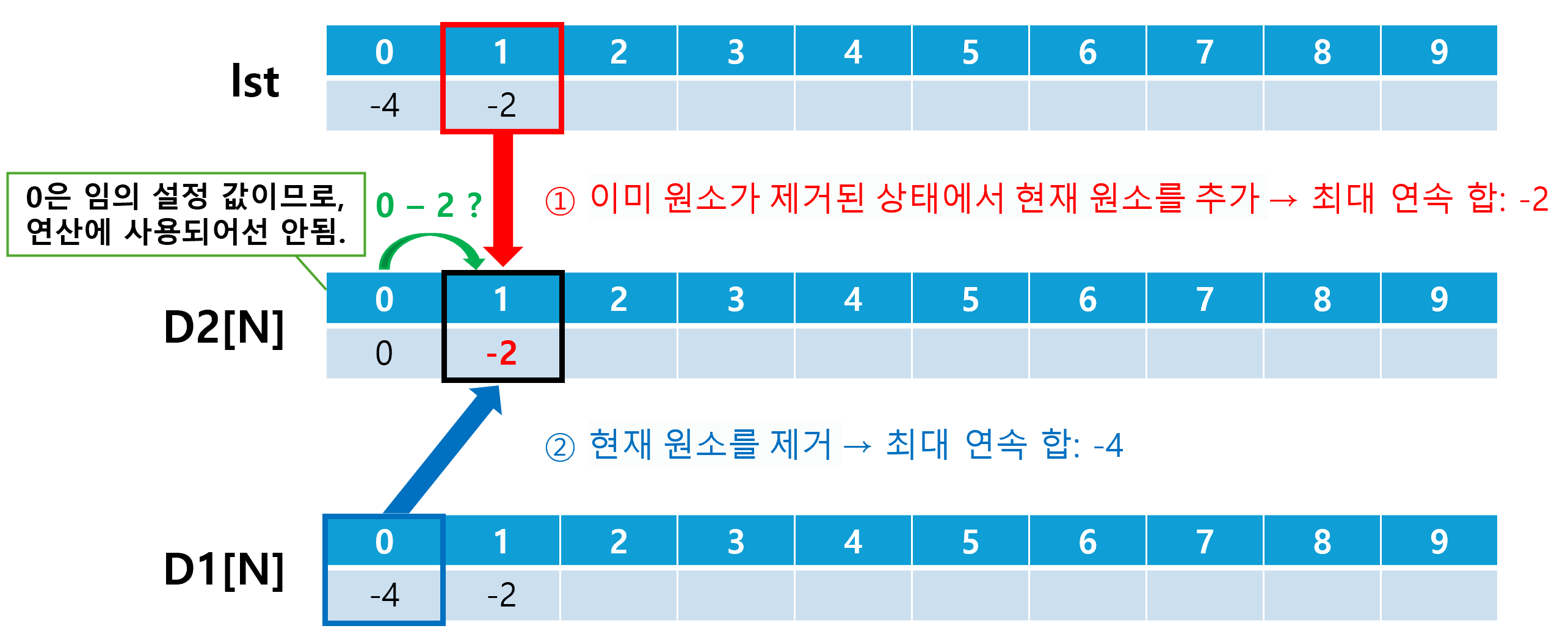
따라서, D2[0]를 이용해서는 최적의 값을 얻지 못하도록, 예외 처리를 해야 한다.
5. 점화식 세울 때 주의할 점
DP 문제는 아래의 두 가지 경우로 구분할 수 있다.
① 최적 값의 위치를 알고 있는 경우
- 최적 값의 인덱스가 고정되어 있는 경우를 의미한다.
- 예를 들어, DP 테이블의 마지막 인덱스에 최적 값이 위치하거나, DP 테이블의 원소를 전체 합한 결과가 최적 값이 되는 경우 등이 해당된다.
- 이번 포스팅을 기준으로 1, 2, 3번 문제가 최적 값의 위치를 알고 있는 경우에 해당된다.
② 최적 값의 위치를 알 수 없는 경우
- 최적 값의 인덱스가 고정되어 있지 않은 경우를 의미한다.
- 예를 들어, DP 테이블의 원소 중 최대 값이 곧 최적 값이 되는 경우 등이 해당된다.
- 이번 포스팅의 4번 문제가 최적 값의 위치를 알 수 없는 경우에 해당한다.
최적 값의 위치를 알 수 없는 경우의 문제에서 점화식(DP 테이블)을 정의할 때, 주의해야 할 부분이 있다. 이 부분에 대해 설명하기 위해 4번 문제를 단순화시킨 아래의 문제를 예시로 살펴보기로 한다. 아래의 문제는 4번 문제에서 원소 제거 옵션만 없앤 문제로, 4번 문제 풀이 중 "원소를 제거하지 않은 상태에서의 최대 연속 합"만 구하면 되는 문제이다.
이 문제를 처음 보았다고 생각하고, DP 테이블을 정의해보자. 흔히 D[N]을 "0에서 N까지 길이에서 연속으로 수를 선택하여 구할 수 있는 최대 합"으로 정의하는데, 이는 잘못된 정의이다. 왜 잘못된 정의인지 알아보기 위해 직접 DP 테이블을 채워보기로 하자.
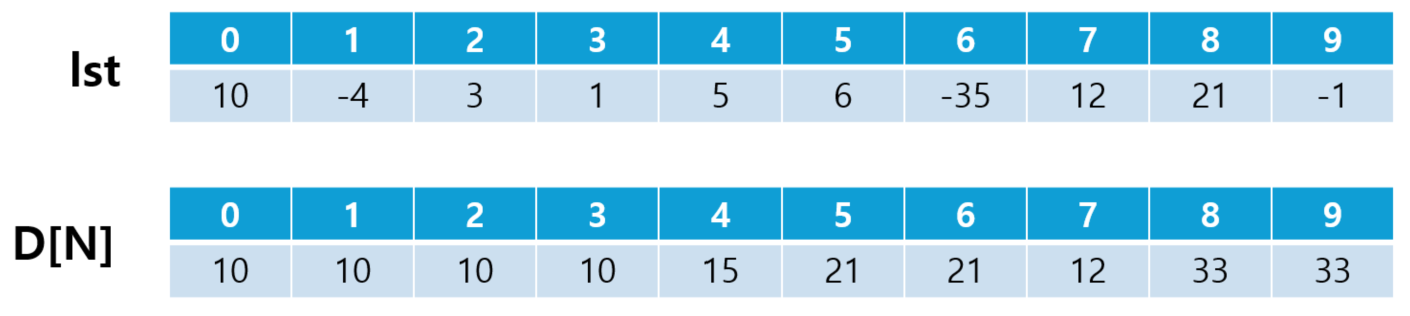
① 최적 부분 구조 위배
- N ≥ n을 만족하는 n에 대해 D[n]과 D[n-1] 사이의 관계가 명확하지 않다.
- 즉, D[n]을 구하는 데에 D[n-1]이 사용될 수도, 사용되지 않을 수도 있다.
② 중복 부분 문제 위배
- Memoization이나 Tabulation이 전혀 활용되지 않고 있다.
- 이와 같이 부분 문제가 명확하지 않은 경우, 부분 문제가 해결하기 어려운 또 다른 문제가 되어버리며, 중복된 계산을 회피하기도 어려워진다.
이와 같은 문제가 발생한 이유는 위 문제를 "최적 값의 위치를 알고 있는 경우"로 풀이하려 했기 때문이다. 그러나, 위 문제는 "최적 값의 위치를 알 수 없는 경우"로 분류하여 풀이했어야 한다.
※ 두 가지 경우를 분류하는 기준
안타깝게도 두 가지 경우를 분류하는 명확한 기준을 만들기는 어렵다. 하지만, 문제를 여러 번 풀이하다보면, 충분히 체득할 수 있는 부분일 것으로 생각된다. 만약 분류하는 일이 어렵게 느껴진다면, "최적 값의 위치를 알고 있는 경우"로는 점화식을 세울 수 없을 때(D[n]과 D[n-1] 사이의 관계가 명확하지 않을 때), "최적 값의 위치를 알 수 없는 경우"로 풀이한다고 생각해도 된다.
최적 값의 위치를 알 수 없는 경우에 대해 DP 테이블을 정의할 때에는 반드시 현재 인덱스의 값을 포함하여 정의해야 한다. 이 내용을 적용하여 점화식을 재정의하면, D[N]은 "0에서 N까지 길이에서 N을 포함하며 연속으로 수를 선택하여 구할 수 있는 최대 합"으로 정의될 것이다. 이제 이 정의를 이용하여 다시 DP 테이블을 구성해보자.
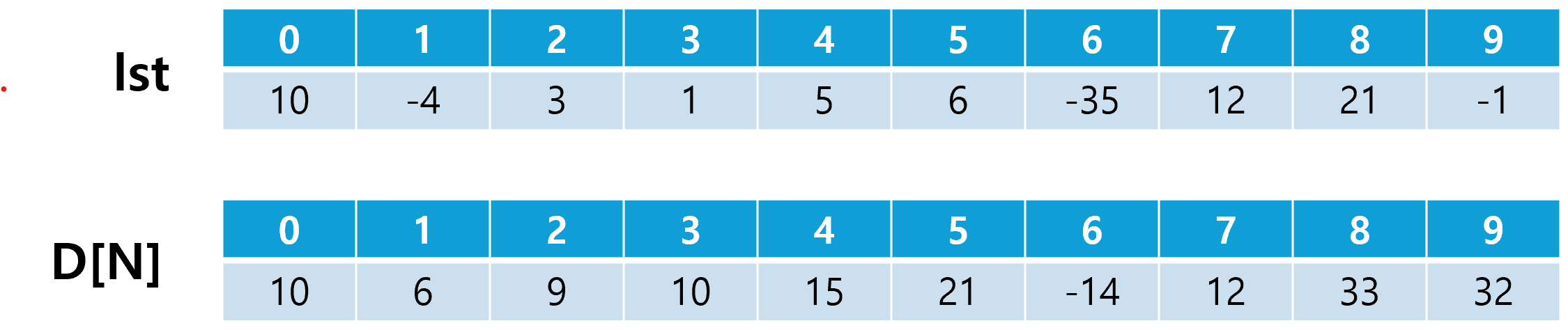
D[N]과 D[N-1]의 관계가 D[N] = max(lst[N], D1[N-1] + lst[N])으로 명확해진 것을 확인할 수 있으며, 부분 문제도 매우 간단해졌다.
위 내용은 DP 문제를 풀이할 때, 반드시 숙지하고 있어야 하는 중요한 내용이므로, 잘 이해해두기 바란다.