1. 동적 계획법
1) 개념
동적 계획법은 복잡한 문제를 간단한 하위 문제로 나눈 후, 하위 문제를 해결함으로써 최종적으로 복잡한 문제의 해답을 구하는 알고리즘 설계 기법이다. 동적 계획법은 중복된 계산을 제거함으로써 시간 복잡도를 낮출 수 있다는 장점이 있지만, 부분 문제의 해답을 모두 저장해야 한다는 점에서 공간 복잡도가 높다는 단점이 있다.
2) DP 적용 조건
동적 계획법을 적용하여 풀이할 수 있는 문제는 반드시 아래의 조건을 만족한다.
① 최적 부분 구조(Optimal Substructure)
- 문제의 최적 해결책이 그 하위 문제들의 최적 해결책으로 구성될 수 있는 경우를 의미한다.
- 즉, 큰 문제를 작은 문제로 나누고, 작은 문제들의 해결책을 결합하여 큰 문제의 해결책을 찾을 수 있다.
- N의 크기에 상관 없이 하위 문제의 결과는 항상 동일해야 한다.
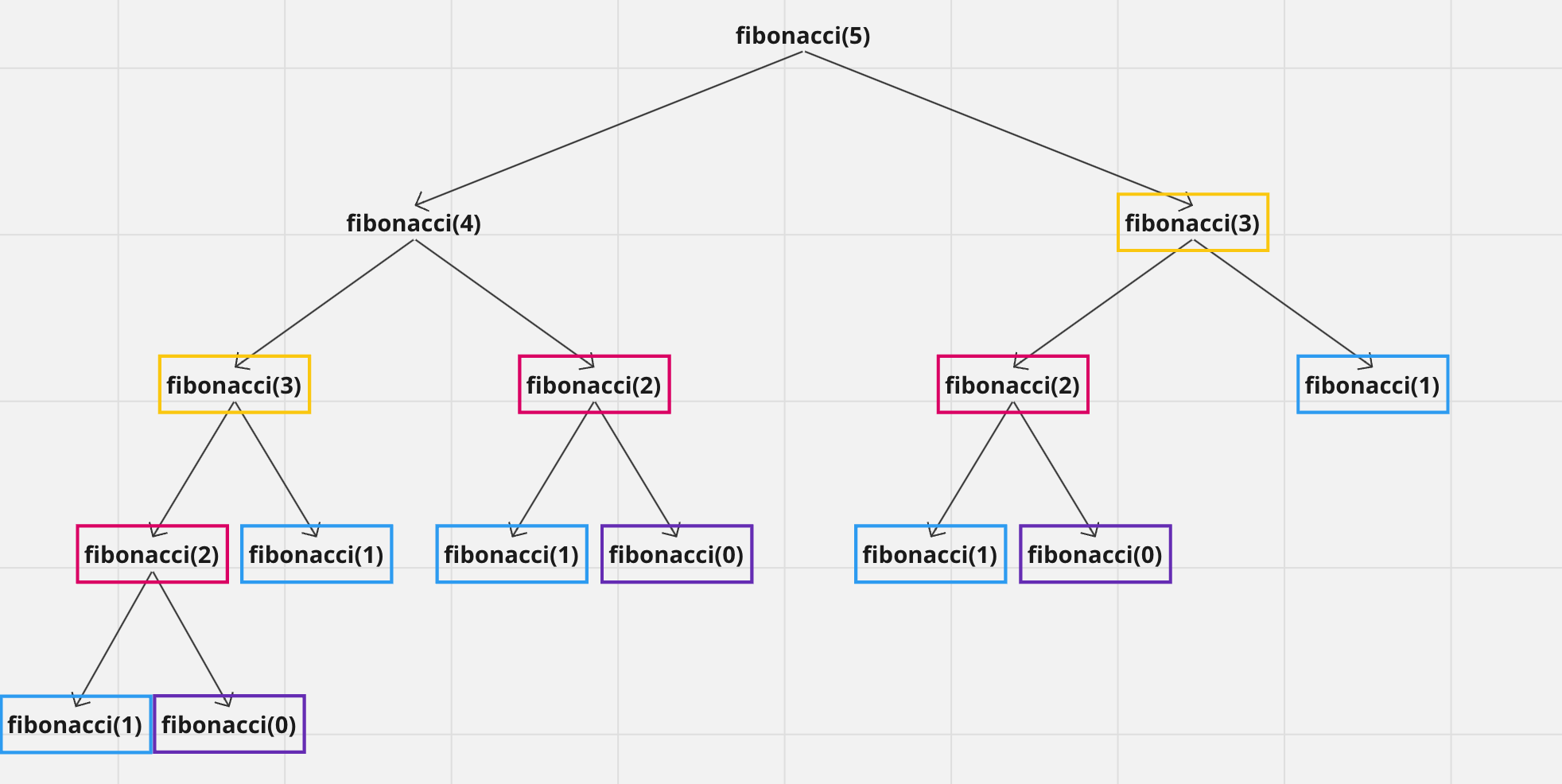
- 예시: 6번째 피보나치 수열은 4번째 피보나치 수열과 5번째 피보나치 수열의 합으로 구성된다. 또한 N의 값에 무관하게 피보나치 수열의 값은 항상 동일하다.
② 중복 부분 문제(Overlapping Subproblems)
- 동일한 부분 문제가 여러 번 반복 계산되는 경우를 의미한다.
- 이러한 중복 계산은 최초 한번만 계산하고, 이후에는 DP 테이블에 저장된 값을 재사용한다.
- 예시: 피보나치 수열을 구하는 과정에서 동일한 부분 문제가 여러 번 반복된다.
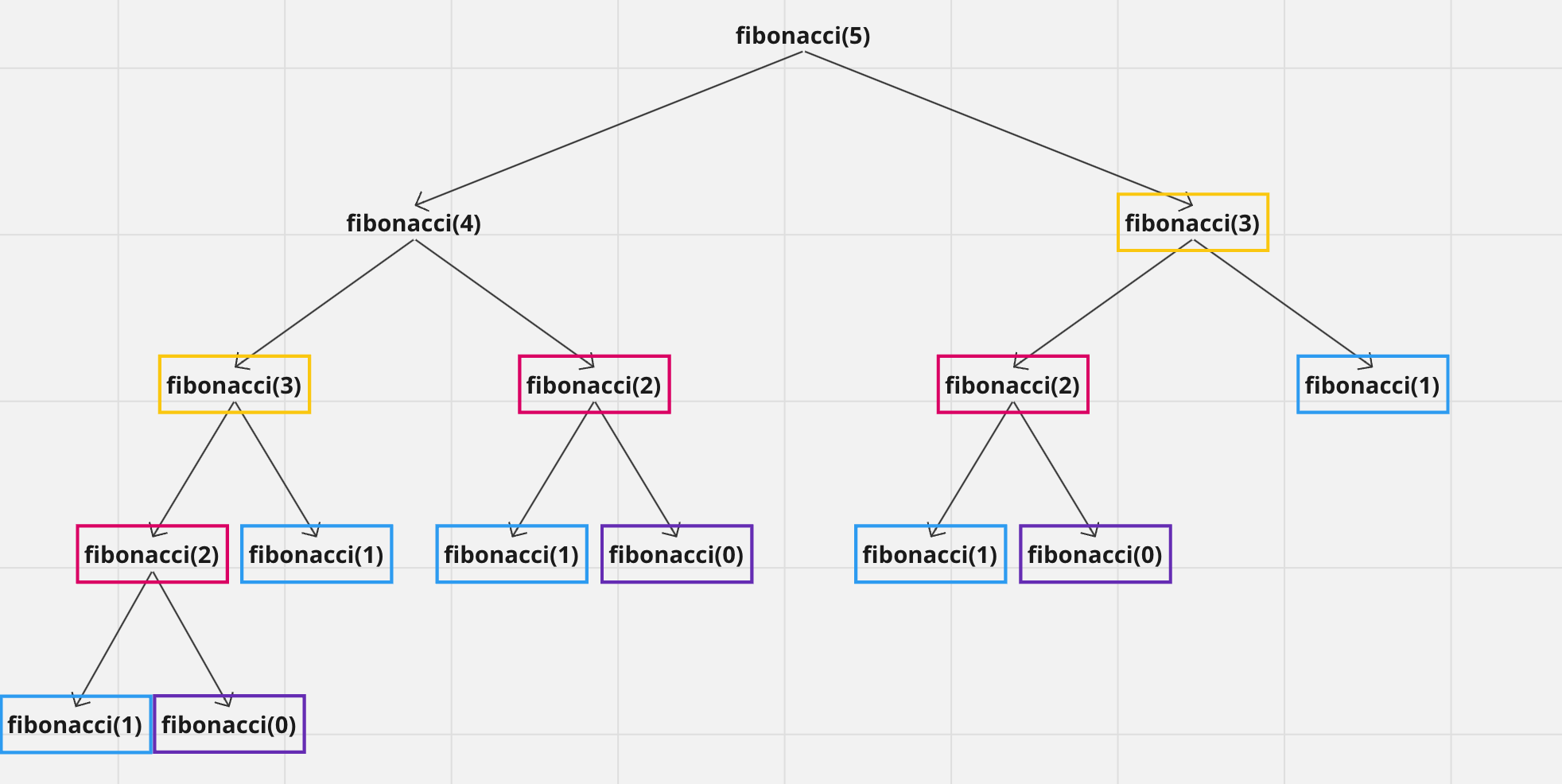
피보나치 수열은 최적 부분 구조와 중복 부분 문제 조건을 만족하므로, DP를 적용하여 구할 수 있다.
3) 접근 방식
① Top-Down Approach(하향식 접근)
- 재귀 호출을 활용한다.
- 중복 계산을 회피하기 위해 Memoization 기법을 활용한다.
import sys
input = sys.stdin.readline
N = int(input())
D = [-1] * (N + 1) # Memoization 되지 않은 원소를 구분한기 위해 0이 아닌 -1로 초기화
D[0] = 0
D[1] = 1
def fibo(n):
if D[n] != -1:
return D[n] # 이미 저장되어 있는 데이터인 경우 재사용
D[n] = fibo(n-2) + fibo(n-1) # 재귀 호출 및 Memoization 활용
return D[n] # return fibo[n-2] + fibo[n-1]의 형식으로 작성했다면, 매번 중복된 계산을 반복했을 것임
fibo(N)
print(D[N])② Bottom-Up Approach(상향식 접근)
- 반복문을 활용한다.
- 중복 계산을 회피하기 위해 Tabulation 기법을 활용한다.
import sys
input = sys.stdin.readline
N = int(input())
D = [0] * (N + 1)
# D[0] = 0
D[1] = 1
for n in range(2, N + 1):
D[n] = D[n - 2] + D[n - 1] # 반복문 및 Tabulation 활용
print(D[N])참고로, Memoization과 Tabulation은 모두 중복 계산을 회피하기 위한 목적은 동일하지만, 약간의 차이가 있다. Memoization은 실제 계산을 수행해야 할 때 데이터를 저장하는 반면, Tabulation은 모든 하위 문제에 대한 해답을 미리(계산이 필요한 시점보다 먼저) 테이블에 저장해둔다.
일반적으로 재귀 호출보다는 반복문의 성능이 더 좋기 때문에, DP에서는 주로 Bottom-Up Approach를 사용한다.
4) 분할 정복법과의 비교
동적 계획법은 복잡한 문제를 하위 문제로 분할한다는 점에서 분할 정복법과 비슷하다. 그러나, 동적 계획법과 분할 정복법에는 아래와 같은 차이점이 존재한다.
① 하위 문제의 중복성
- 동적 계획법: 중복되는 하위 문제를 효율적으로 해결한다.
- 분할 정복법: 하위 문제를 독립적으로 해결한다.
② Meomiazation의 필요성
- 동적 계획법: 하위 문제에 대한 해답을 저장해두었다가, 상위 문제에서 재사용한다.
- 분할 정복법: 하위 문제에 대한 해답을 저장할 필요가 없다.
③ 접근법
- 동적 계획법: 주로 Bottom-Up Approach를 사용한다.
- 분할 정복법: 주로 Top-Down Approach를 사용한다.
2. 문제 풀이
1) 정수를 1로 만들기
문제를 보자마자 떠올리기 쉬운 접근법은 아무래도 BFS일 것이다.
import sys
input = sys.stdin.readline
from collections import deque
N = int(input())
visited = [-1] * (N + 1)
deq = deque()
def bfs(V):
deq.append(V)
visited[V] = 0
while deq:
V = deq.popleft()
if V == 1:
break
if V % 3 == 0 and visited[V // 3] == -1:
deq.append(V // 3)
visited[V // 3] = visited[V] + 1
if V % 2 == 0 and visited[V // 2] == -1:
deq.append(V // 2)
visited[V // 2] = visited[V] + 1
if visited[V - 1] == -1:
deq.append(V - 1)
visited[V - 1] = visited[V] + 1
bfs(N)
print(visited[1])그러나 이 문제는 DP를 활용하여 풀이할 수도 있다. 동적 계획법 문제를 자주 풀다보면, DP를 이용해 푸는 문제임을 알아차리는 감각이 생긴다. 하지만, 처음 문제를 보자마자 DP를 떠올리기는 쉽지 않을 수 있다. 이럴 때에는 원시적인 접근법으로 풀이법에 대한 힌트를 찾아내야 한다. 일단은, 10을 1로 만드는 데 필요한 연산 횟수의 최소 값을 직접 계산해보기로 하자.
먼저 10에서 1을 빼거나, 2로 나눌 수 있을 것이다. 그러면 이제 9 또는 5를 1로 만들기 위해 9를 3으로 나누거나, 5에서 1을 빼야 한다. 또 다음에는 3을 3으로 나누거나, 4를 2로 2번 나눔으로써, 최종적으로 1을 얻게 된다.
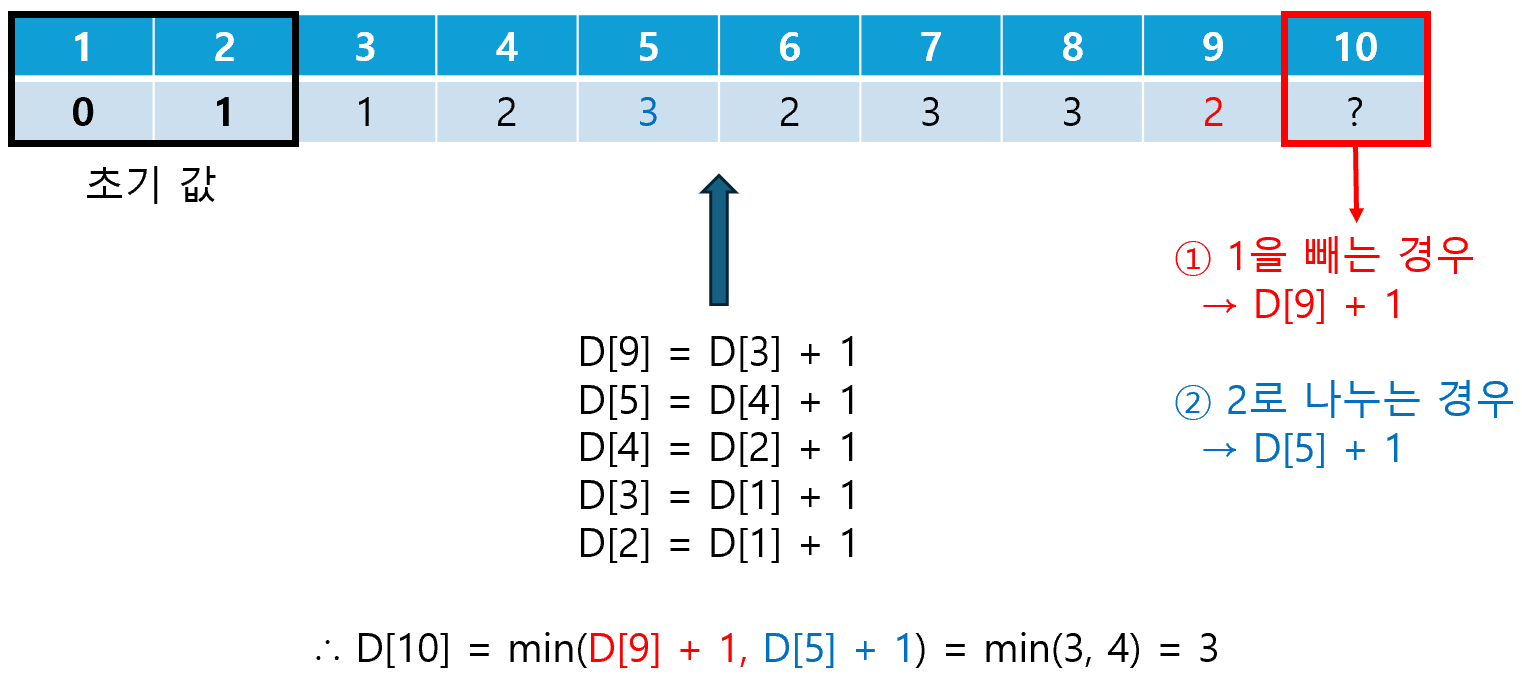
10번째 원소를 구하기 위해 5번째 원소 또는 9번째 원소가 활용된다는 점에서, 위 문제가 최적 부분 구조를 만족한다는 사실을 확인할 수 있다. 또한, DP 테이블을 채워가는 과정에서 동일한 부분 문제가 반복된다는 사실도 쉽게 확인해볼 수 있다. 따라서, 위 문제는 DP를 이용해 풀이할 수 있는 문제이다.
DP 풀이를 결정했다면 가장 먼저 해야 할 일은 점화식을 도출하는 것이다. D[N]을 N을 1로 만드는 데 필요한 연산 횟수의 최소 값이라 정의하면, 아래와 같은 점화식을 도출해낼 수 있다.
D[n] = D[n-1] + 1 # 1을 빼는 연산
if (n % 2 == 0) D[n] = min(D[n], D[n // 2] + 1) # 2로 나누는 연산
if (n % 3 == 0) D[n] = min(D[n], D[n // 3] + 1) # 3으로 나누는 연산위 점화식은 1을 빼는 경우, 2로 나누는 경우, 3으로 나누는 경우 중 최소가 되는 값으로 DP 테이블을 업데이트 한다. 비록 D[10]을 바로 구하는 일은 복잡하고 어려운 일이지만, D[2]부터 차근차근 DP 테이블을 채워나가다보면(Bottom-Up Approach), 자연스레 D[10]의 값이 구해질 것이다.
import sys
input = sys.stdin.readline
N = int(input())
D = [0] * (N + 1) # D[1] = 0
for n in range(2, N + 1):
D[n] = D[n - 1] + 1
if n % 2 == 0: # n이 2로 나누어 떨어지면
D[n] = min(D[n], D[n // 2] + 1) # D[n]을 최소 값으로 업데이트
if n % 3 == 0: # n이 3으로 나누어 떨어지면
D[n] = min(D[n], D[n // 3] + 1) # D[n]을 최소 값으로 업데이트
print(D[N])대부분의 DP 문제가 그러하듯 점화식 도출에만 성공한다면, 어렵지 않게 풀 수 있는 문제이다.
2) 퇴사 준비하기
이 문제도 최적 부분 구조와 중복 부분 문제를 만족한다. 그 이유는 D[n]을 n일차까지 얻을 수 있는 최대 이익이라 할 때, D[7]은 그 전까지의 이익을 고려하여 계산되어야 하며, DP 테이블을 채워가는 과정에서 동일한 부분 문제가 반복되기 때문이다.
이제 점화식을 세울 차례이다. n일차에서 백준이는 아래의 두 가지 경우 중 하나를 선택할 수 있다.
- 오늘의 상담을 진행하기로 결정
- 상담 일정이 N일을 초과할 경우 진행 불가
- 상담 종료일의 DP 테이블 값을, 기존 값과 n일차까지의 최대 수익에 오늘의 상담 이익을 더한 수치를 비교하여 더 큰 값으로 업데이트
- 점화식:
D[n + time] = max(D[n + time], D[n] + profit)
- 오늘의 상담을 포기하기로 결정
- 내일까지의 최대 이익을 기존 값과 오늘까지의 최대 이익 중 더 큰 값으로 업데이트
- n + 1이 N을 초과하지 않도록 예외 처리
- 점화식:
D[i + 1] = max(D[i + 1], D[i])
이제 각각의 경우에 대해 점화식을 활용하여 최대 이익을 계산하면 된다.
import sys
input = sys.stdin.readline
N = int(input())
schedule = [list(map(int, input().split())) for _ in range(N)] # 상담 일정표
D = [0 for i in range(N + 1)] # i일차까지 얻을 수 있는 최대 이익
for i in range(N):
time, profit = schedule[i][0], schedule[i][1]
# 현재 상담을 선택하는 경우
if i + time <= N: # 상담 일정이 N일을 초과할 경우 진행 불가
D[i + time] = max(D[i + time], D[i] + profit)
# 현재 상담을 선택하지 않는 경우
D[i + 1] = max(D[i + 1], D[i]) # 현재까지의 최대 이익 또는 기존 D[i + 1] 중 더 큰 값으로 업데이트
print(D[N])