1. 다리 놓기
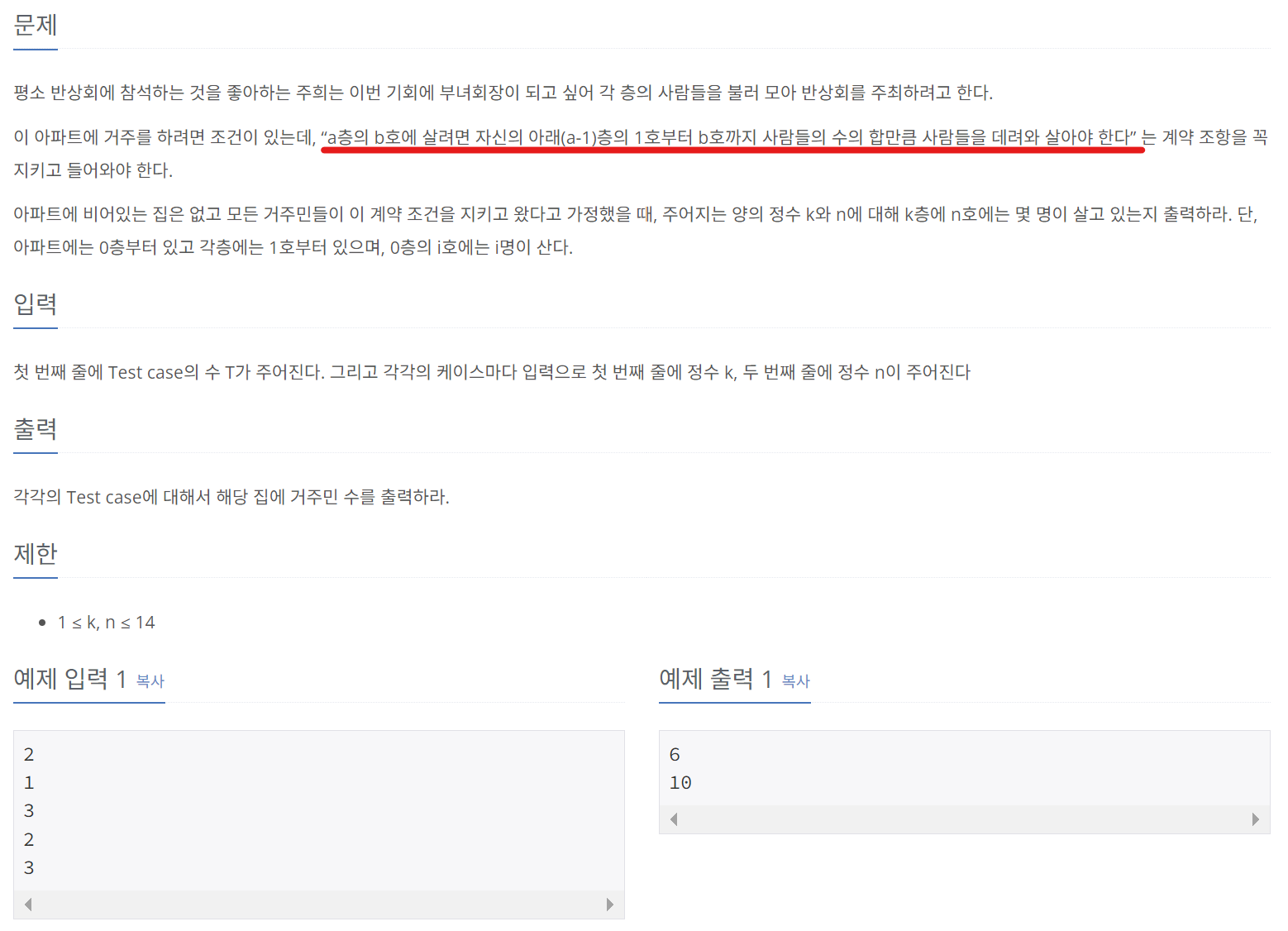
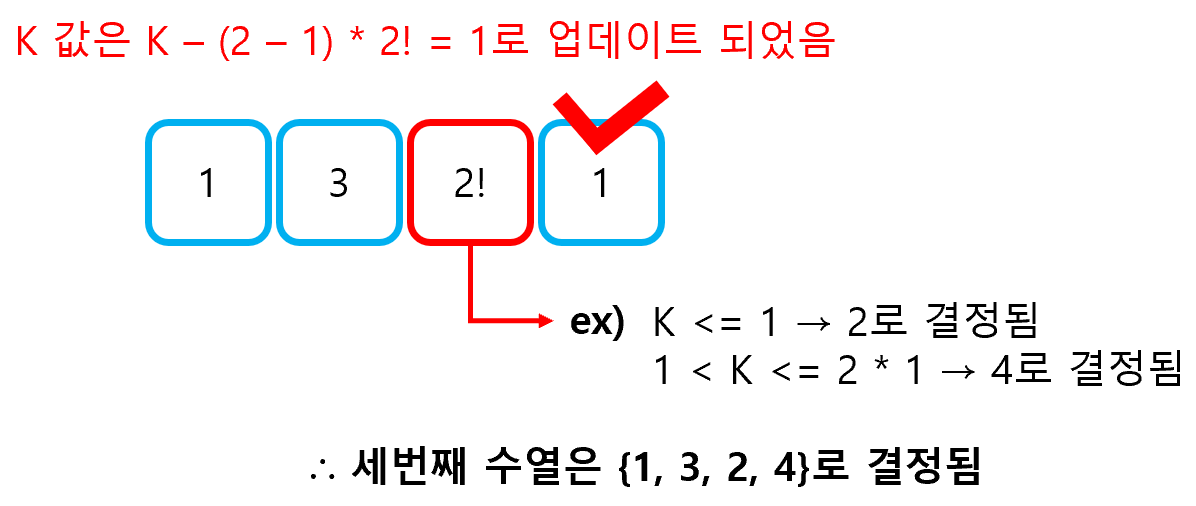
다리끼리 서로 겹쳐지지 않는다는 조건이 있기 때문에 위 문제는 M개의 사이트 중 N개를 선택하는 문제로 해석할 수 있다. 입력 값의 범위가 크지 않기 때문에 직접 조합을 계산하여 풀이해도 무방할 것으로 보인다.
① math 라이브러리를 이용한 풀이
import sys
import math
input = sys.stdin.readline
Q = int(input())
for i in range(Q):
N, M = map(int, input().split())
result = math.comb(M, N)
print(result)② 점화식을 이용한 풀이
import sys
input = sys.stdin.readline
Q = int(input())
# M을 행으로, N을 열로 하는 테이블 생성
D = [[0 for col in range(31)] for row in range(31)]
# 테이블 초기화
for i in range(31):
D[i][0] = 1
D[i][1] = i
D[i][i] = 1
for _ in range(Q):
N, M = map(int, input().split())
for i in range(3, M + 1):
for j in range(1, i):
D[i][j] = D[i - 1][j] + D[i - 1][j - 1]
print(D[M][N])2 부녀회장이 될테야
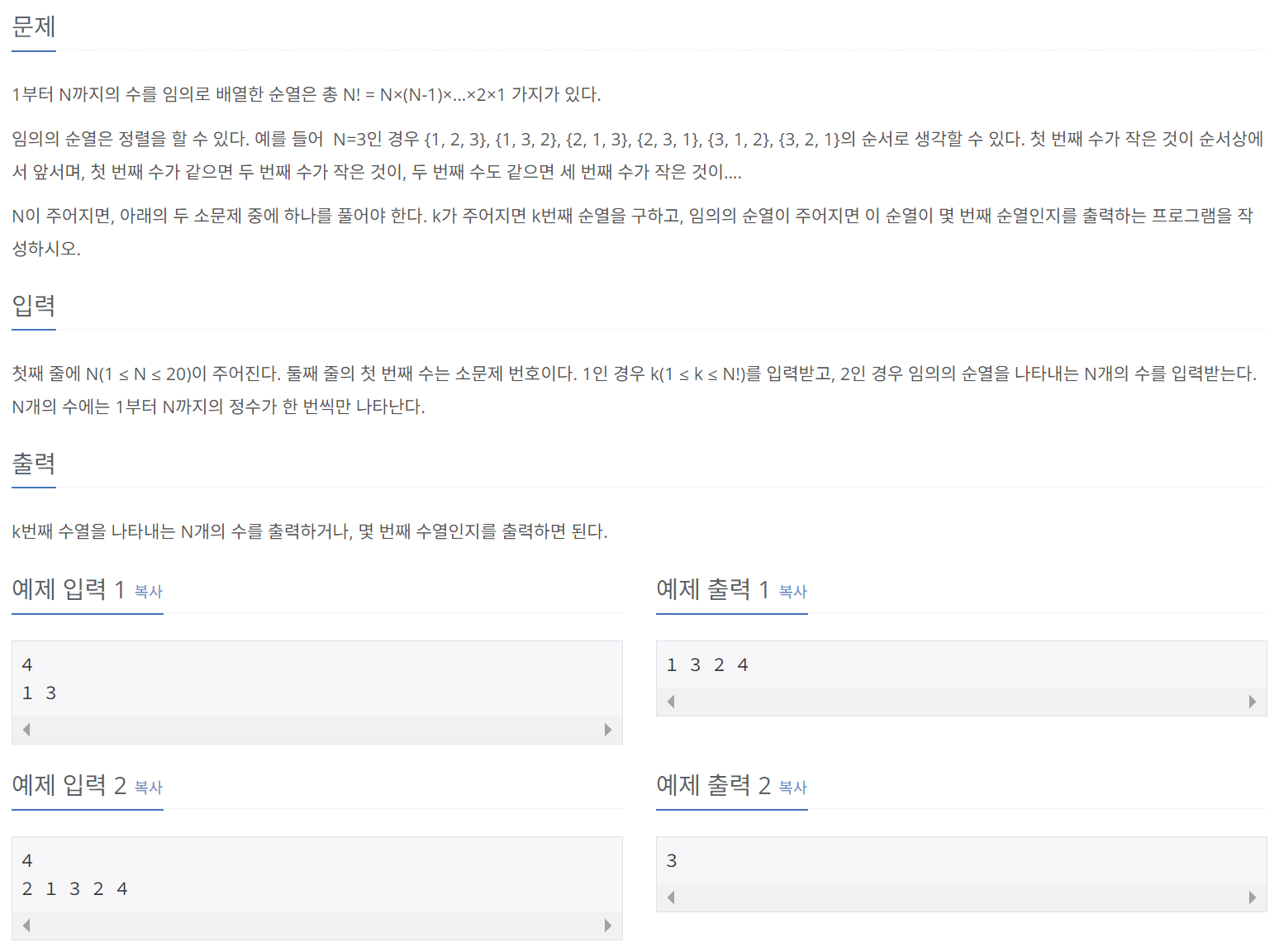
점화식의 개념을 도입하여 조합을 설명한 이유가 바로 위와 같은 문제를 잘 풀기 위함이다. 위 문제는 조합의 개념과는 거리가 멀지만, 점화식을 활용하여 문제를 풀이할 수 있다는 점에서 일맥상통하다. 먼저, 위 문제의 조건을 점화식의 형태로 나타내어보자.
조건식을 그대로 쓰면, D[a][b] = D[a-1][0] + D[a-1][1] + ... + D[a-1][b-1] + D[a-1][b]가 되는데, 여기서 D[a-1][0] + D[a-1][1] + ... + D[a-1][b-1]는 D[a][b-1]로 바꿔 쓸 수 있으므로, D[a][b] = D[a][b-1] + D[a-1][b]라는 점화식을 도출할 수 있다. 이제 이 점화식을 기반으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
# n의 최대값이 14이므로, 15 X 15 사이즈의 테이블 생성
D = [[0 for col in range(15)] for row in range(15)]
# 테이블 초기화
for i in range(15):
D[0][i] = i # 문제의 조건: 0층의 i호에는 i명이 산다.
D[i][1] = 1 # 0층의 1호에는 1명이 살기 때문에 모든 층의 1호에는 1명만 살아야 한다.
# 점화식을 이용하여 테이블 값 업데이트
for i in range(1, 15): # 0층에 대해서는 초기화가 완료된 상태이므로, 1층부터 시작
for j in range(2, 15): # 각 층의 1호에 대해서는 초기화가 완료된 상태이므로, 2호부터 시작
D[i][j] = D[i][j-1] + D[i-1][j]
Q = int(input())
for i in range(Q):
a = int(input())
b = int(input())
print(D[a][b])3. 순열의 순서 구하기
1) 첫번째 소문제
먼저 K번째 수열을 알아내는 방법에 대해 생각해보자. (N = 4, K = 3으로 가정하며, 맨 오른쪽부터 첫째 자리로 생각한다.)
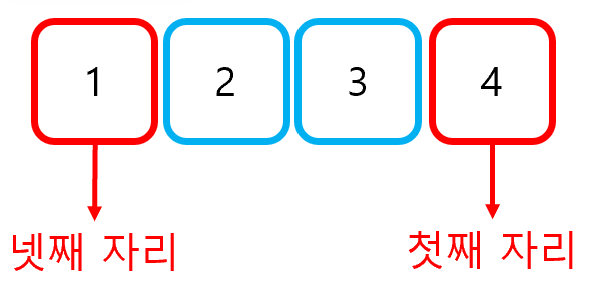
먼저 넷째 자리가 1이 되는 경우의 수를 구해보자. 1은 이미 배치되었으므로, 경우의 수는 당연히 3!이 될 것이다. 이는 넷째 자리가 2, 3, 4가 되는 경우에 대해서도 마찬가지로 적용된다. 이 사실을 이용하면, 첫 자리를 결정지을 수 있게 된다. 여기서는 K가 3이므로, 첫 자리는 1이 될 것이다.
즉, n번째 자리의 숫자를 결정하기 위해서는 (n - 1)!의 값을 이용해야 하는 것이다.

이와 같은 방식으로 K번째 수열을 알아낼 수 있다. 다만, 주의해야 할 것은 N번째 자리의 수가 결정된 이후부터는 남은 수만 활용하여 숫자를 결정해야 한다는 것이다.
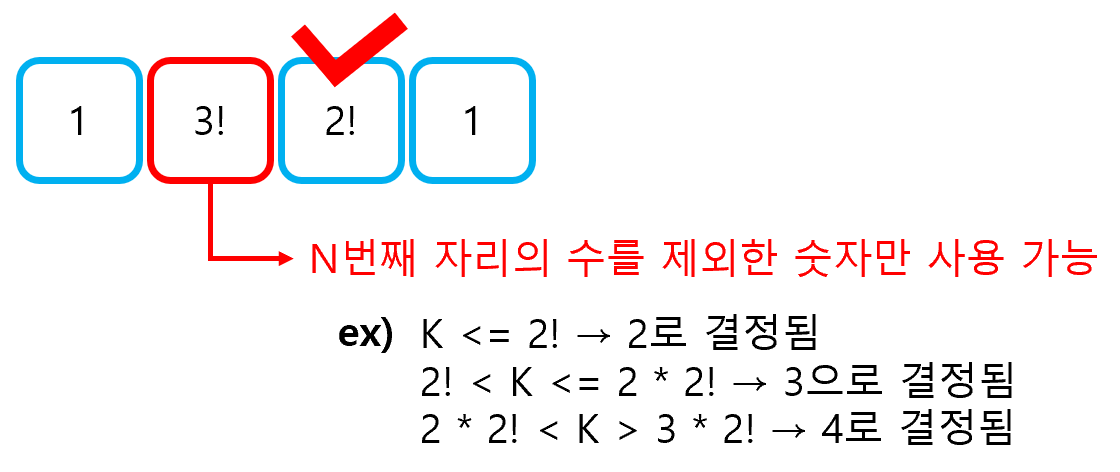
이 때, K <= C * (n-1)!가 성립하는 어떤 C에 대해, K 값을 K - (C - 1) * (n-1)!로 업데이트해야 한다. 그 이유는 이미 결정되어 있는 몇몇 자리수가 K 값의 정보를 일부 반영하고 있기 때문이다.

이와 같은 방식으로, 3번째 수열이 {1, 3, 2, 4}라는 사실을 알아낼 수 있게 된다.
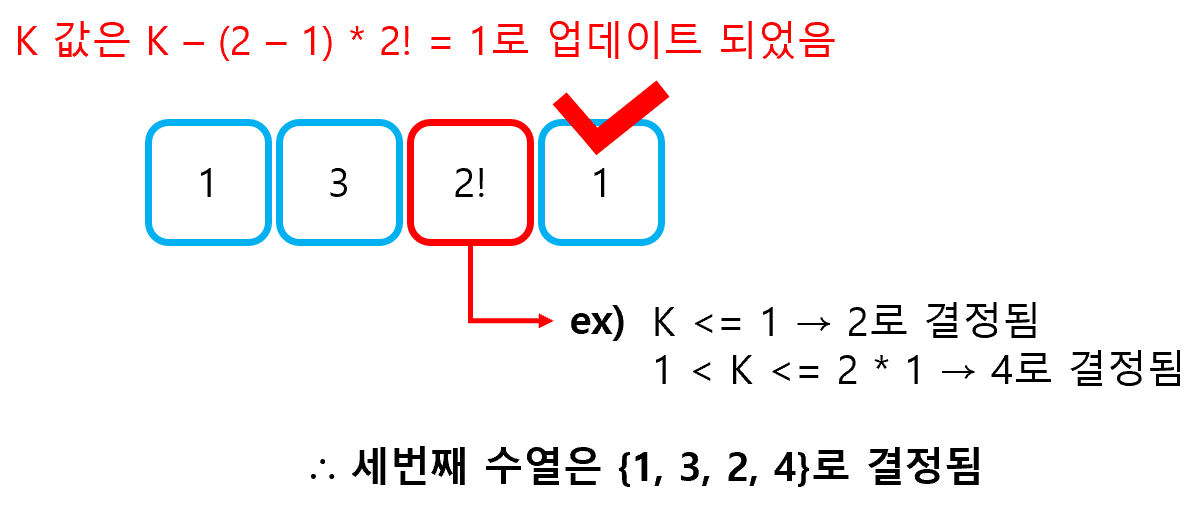
2) 두번째 소문제
이번에는 입력된 수열이 몇번째 수열인지를 찾아내야 한다. 이 문제에도 첫번째 소문제를 풀이할 때 사용했던 방식을 그대로 적용할 것이다. 먼저 K를 1로 초기화한 후, 최적의 값이 아닌 n번째 자리 수에서 C * (n-1)!의 값을 더하여 몇번째 수열인지를 계산할 것이다. 참고로 여기서의 C는 n번째 자리 수보다 작으면서, 아직 사용되지 않은 숫자의 개수이다.
예를 들어, {1, 3, 2, 4}의 수열에서 셋째 자리가 3이라는 의미는, 해당 수열이 적어도 셋째 자리가 2인 수열보다는 뒤에 있다는 뜻이다. 따라서, K의 값을 2!만큼 증가시킨다. 그 외의 자리 수는 이미 최적의 값을 가지고 있으므로, 더 이상 K의 값을 증가시키지 않아도 된다.
만약 주어진 수열이 {1, 4, 2, 3}이었다면, 세번째 자리 수보다 작으면서, 아직 사용되지 않은 숫자는 두 개이므로(2와 3), K의 값을 2 * 2!만큼 증가시켜야 했을 것이다.
3) 최종 풀이
import sys
input = sys.stdin.readline
fact = [1] * 21 # 팩토리얼 값을 저장하고 있는 배열, 0!를 0으로 초기화하지 않도록 주의
for i in range(1, 21): # 팩토리얼 값 계산
fact[i] = fact[i-1] * i # math.factorial()을 이용하는 것보다 훨씬 효율적인 방법
visited = [0] * 21 # 숫자 사용 여부 저장하고 있는 배열
answer = [0] * 21 # 1번 소문제에 대한 정답 수열을 저장하는 배열
N = int(input())
query = list(map(int, input().split()))
if query[0] == 1: # 1번 소문제
K = query[1]
for i in range(1, N + 1): # 넷째자리 -> 셋째자리 -> 둘째자리 -> 첫째자리
C = 1 # (N-1)!의 계수
for j in range(1, N + 1): # 1, 2, 3, 4 중 사용할 숫자를 결정
if visited[j] == 0: # 아직 사용하지 않은 숫자만 사용 가능
if K <= C * fact[N - i]: # N번째 자리의 숫자를 결정하기 위해서는 (N - 1)!의 값을 이용해야 함
K -= (C - 1) * fact[N - i] # K 값을 K - (C - 1) * (N-1)!로 업데이트
answer[i] = j # 정답 수열에 값 할당
visited[j] = 1 # 숫자 사용 여부 업데이트
break
else:
C += 1
for i in range(1, N + 1):
print(answer[i], end=' ')
else: # 2번 소문제
K = 1 # K를 1로 초기화
for i in range(1, N + 1): # 넷째자리 -> 셋째자리 -> 둘째자리 -> 첫째자리
C = 0 # n번째 자리 수보다 작으면서, 아직 사용되지 않은 숫자의 개수
for j in range(1, query[i]): # n번째 자리 수가 최적인 경우에는 수행되지 않음
if visited[j] == 0:
C += 1
K += C * fact[N - i] # 최적의 값이 아닌 n번째 자리 수에 대해, K 값에 C * (n-1)!의 값을 더함
visited[query[i]] = 1 # 숫자 사용 여부 업데이트
print(K)4. 사전 찾기
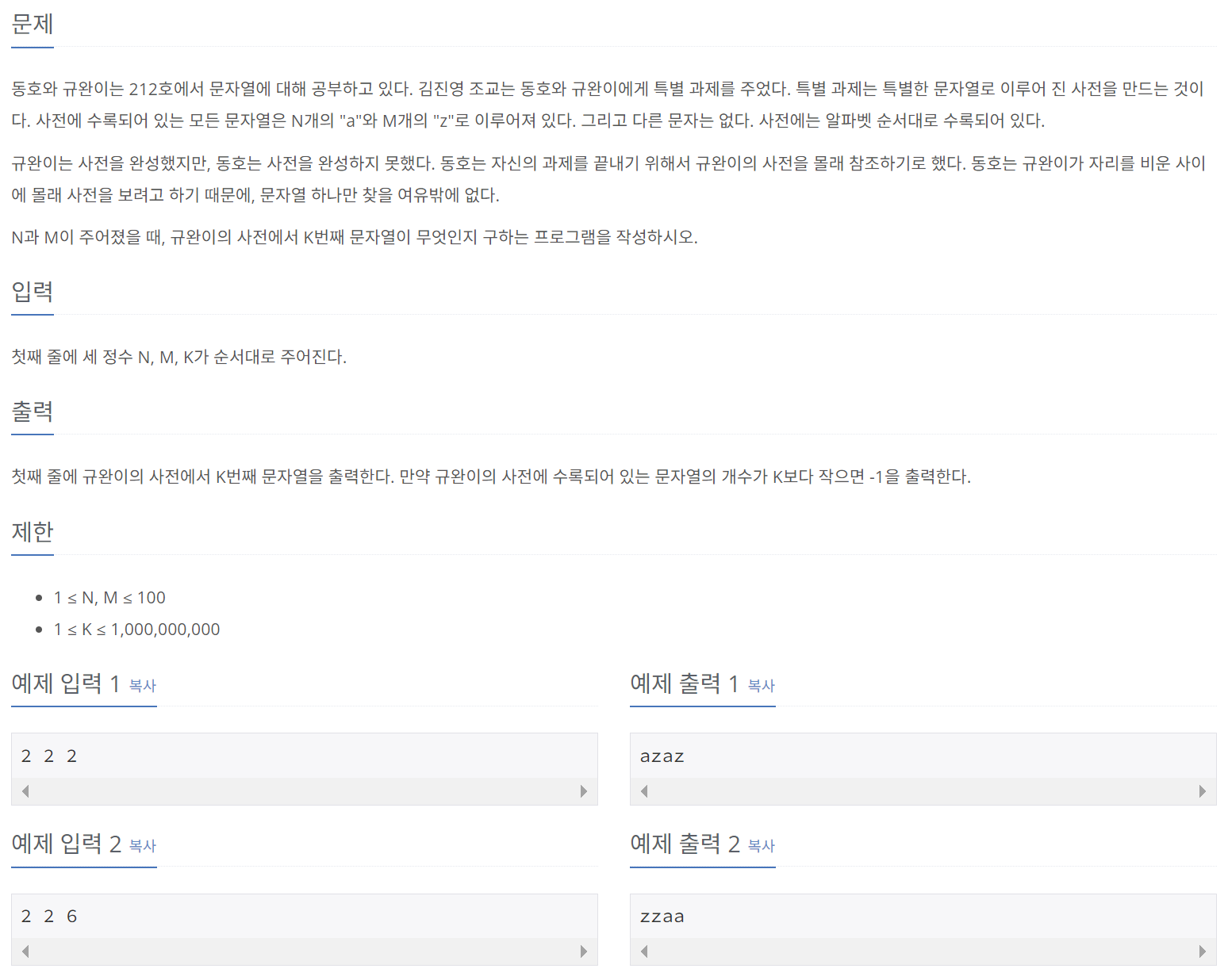
문제를 조금 더 명확히 하기 위해 조건을 하나 추가하자면, 사전에는 N개의 'a'와 M개의 'z'로 만들 수 있는 모든 문자열이 전부 수록되어 있는 상태이다.
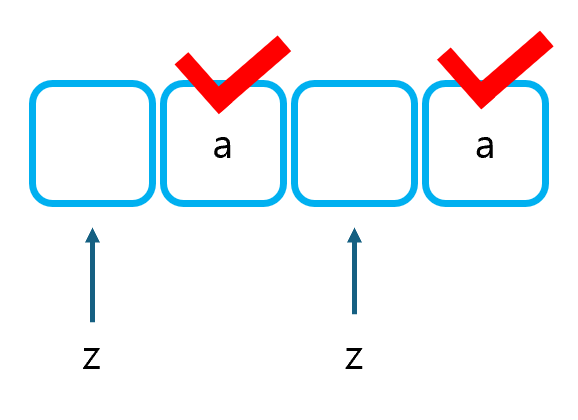
먼저 알아야 할 것은 N개의 'a'와 M개의 'z'로 만들 수 있는 문자열의 개수는 곧 (N + M)개 중 N개(또는 M개)를 고르는 경우의 수와 같다는 것이다. 그 이유는 N = 2, M = 2이라고 할 때, 4개의 빈칸 중 a를 넣을 2칸을 선택하면 z의 위치도 자동으로 결정되기 때문이다. 따라서, 이번에도 조합 테이블을 이용할 것이다.
이제 K번째 문자열을 계산하는 방법에 대해 생각해보자. 현재 자리수에 a를 할당했을 때, 만들 수 있는 문자열의 수를 X라고 가정하자. 이 때, X ≥ K 이면 그대로 a를 선택하고, X < K이면 z로 변경 후 K 값을 K - X로 업데이트한다. 업데이트하는 이유는 3번 문제에서의 이유와 동일하다.
참고로, X 값을 계산하는 방법은 a의 개수와 자리수를 1 줄인 상태에서 만들 수 있는 경우의 수와 같다. 예를 들어, 맨 앞자리에 대한 X 값은 D[N + M - 1][M]이 될 것이다. 이 때, N을 쓰지 않도록 주의해야 한다. (N이 아닌 N-1을 넣어야 하는데, N-1은 번거로우므로 M을 쓴다.)
import sys
input = sys.stdin.readline
N, M, K = map(int, input().split())
D = [[0 for col in range(201)] for row in range(201)]
# 테이블 초기화
for i in range(201):
D[i][0] = 1
D[i][1] = i
D[i][i] = 1
for i in range(3, 201):
for j in range(1, i):
D[i][j] = D[i - 1][j] + D[i - 1][j - 1]
# 문자열의 개수가 K보다 작을 경우 -1 출력
if D[N + M][M] < K:
print(-1)
else:
while not (N == 0 and M == 0):
if D[N + M - 1][M] >= K: # X ≥ K인 경우
print('a', end='') # 그대로 a를 선택
N -= 1 # 사용 가능한 a의 개수가 1 감소
else:
print('z', end='') # z로 변경
K -= D[N + M - 1][M] # K 값을 K - X로 업데이트
M -= 1 # 사용 가능한 z의 개수가 1 감소
5. 선물 전달하기
1) 점화식 도출
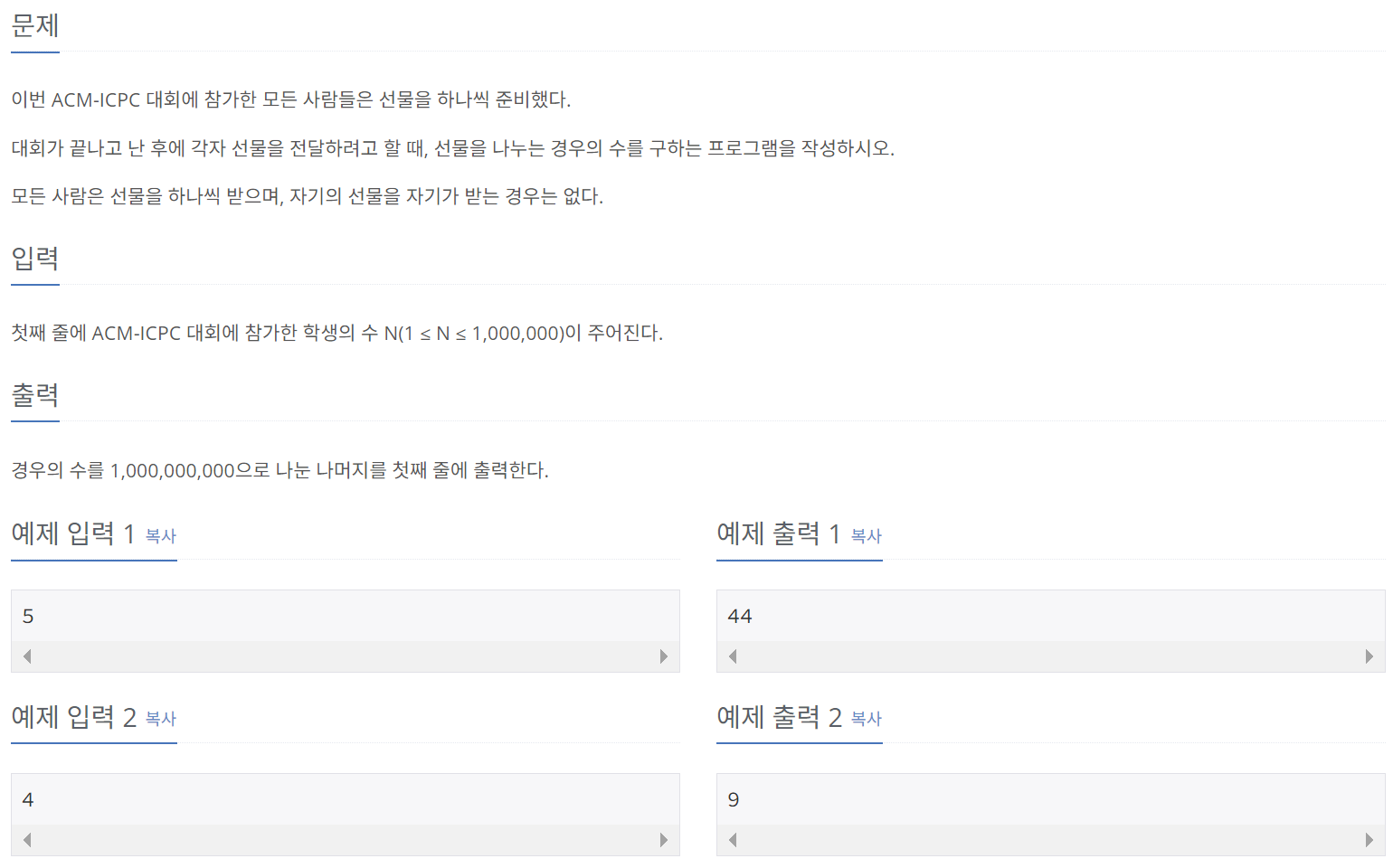
n개의 원소의 집합에 대해 원소를 재배열할 때, 단 하나의 원소도 원래의 위치에 배치되지 않는 순열을 완전 순열이라 한다. 물론, 완전 순열의 점화식을 암기해두는 것도 좋은 방법이다. 그러나, 나중에 동적 계획법을 배울 때, 점화식을 도출해내는 역량이 무엇보다도 중요하기 때문에, 여기서는 단순히 점화식을 알려주는 방식 대신 점화식을 도출하는 방법을 위주로 학습해보겠다.
N명에 대한 완전 순열의 값을 저장하는 D[N] 테이블을 만들어 볼 것이다. 이 때, A가 B에게 선물을 이미 주었다고 가정하면, B에게는 아래의 두 가지 선택지만 남게 된다.
- B도 A에게 선물을 준다.
- B는 A가 아닌 다른 사람에게 선물을 준다.
전자의 경우, 이미 N명 중 2명이 선물 교환을 완료하였으므로, 가능한 경우의 수는 D[N-2]가 될 것이다. 다음으로 후자의 경우, B만 선물이 결정된 상태이므로, 가능한 경우의 수는 D[N-1]이 된다.
처음에 A가 B에게 선물을 주었다고 가정했을 때 경우의 수는 D[N-2] + D[N-1]이지만, 실제로는 A가 (N-1)명에게 줄 수 있으므로, 전체 경우의 수는 (N-1) * (D[N-2] + D[N-1])이 된다. 그리고 이 점화식이 바로 완전 순열의 점화식이 된다.
2) D[N] 테이블 초기화
점화식에서 최대 (N-1)과 (N-2)의 값을 사용하고 있으므로, D[1]과 D[2]를 초기화해야 한다. (1 ≤ N)
① D[1], D[2] 초기화
- N = 1인 경우, 완전 순열이 불가하므로 D[1] = 0으로 초기화된다.
- N = 2인 경우, 두 원소가 서로 교환되는 경우만 가능하므로, D[2] = 1로 초기화된다.
② 나머지 원소 초기화
- 주어진 점화식을 활용하여 나머지 원소에 대한 초기화를 진행한다.
3) 문제 풀이
N = int(input())
# D = [0 for _ in range(N + 1)]
D = [0 for _ in range(1000001)]
D[1] = 0
D[2] = 1
for n in range(3, N + 1):
D[n] = (n - 1) * (D[n - 2] + D[n - 1]) % 1000000000
print(D[N])D[N] 배열을 생성할 때, 위 코드에서 주석 처리된 D = [0 for _ in range(N + 1)]과 같이 작성하지 않도록 주의한다. 그 이유는 N이 1일 때, D[2] = 1 부분에서 IndexError가 발생하기 때문이다. 따라서, 예외처리를 진행하거나 처음부터 N의 최대 범위로 D[N] 배열을 생성해야 한다.