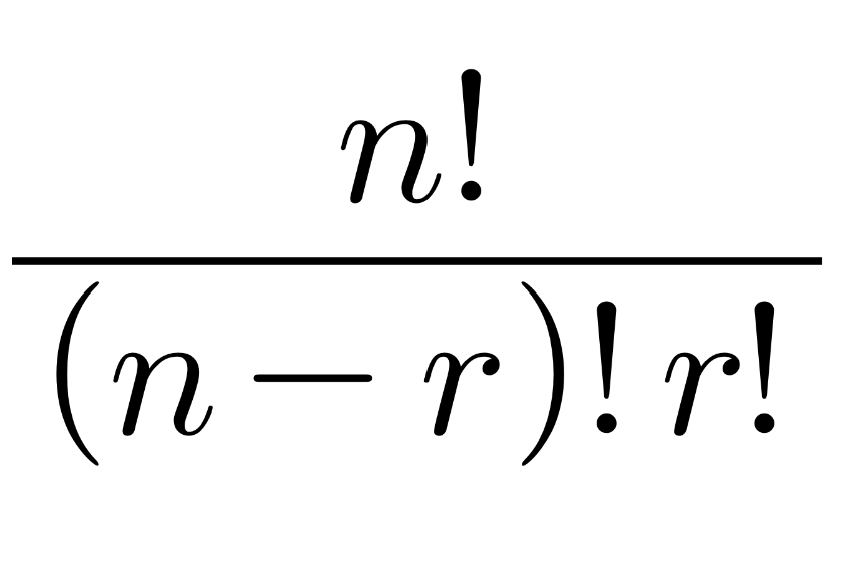
1. 조합
1) 개념
조합은 n개의 원소 중 r개를 선택하는 경우의 수를 의미하며, 수학적 공식으로는 아래와 같이 나타낸다.
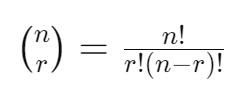
조합의 개념은 그 자체로도 매우 중요하지만, 무엇보다도 나중에 배울 동적 계획법의 기초가 되는 내용이기 때문에 반드시 이해하고 넘어가야 한다.
조합의 개념이 동적 계획법의 기초가 되는 내용이라고 말하는 이유는 조합 계산에 점화식이 사용되기 때문이다. 아마 이 부분에서 "왜 수학 공식을 그대로 사용하지 않는가?"에 대한 의문이 생길 수도 있다. 물론, 단순한 조합 문제의 경우, 공식을 적용하여 풀이할 수 있겠지만, 복잡한 조합 문제를 풀이할 때에는, 공식을 적용하는 방식이 별로 권장되지 않는다. 그 이유는 아래와 같다.
- 팩토리얼 연산의 비효율성: 단순히 계산량이 많은 것뿐 아니라, 빠르게 증가하는 팩토리얼의 특성상 정수 오버플로가 발생할 가능성도 존재한다.
- 코드의 가독성: 코드 상에서의 팩토리얼 및 분수 표현이 수학 공식처럼 깔끔하지 않기 때문에 가독성이 매우 떨어진다.
반면 점화식을 사용할 경우, 중간 계산 결과를 재사용할 수 있기 때문에, 보다 효율적인 계산이 가능해진다. 또한, 각 단계에서 계산되는 값은 팩토리얼보다 상대적으로 작은 값이기 때문에 정수 오버플로의 가능성도 크게 낮출 수 있게 된다. 또한, 복잡한 분수 표현이나 팩토리얼 계산이 불필요하기 때문에, 코드의 가독성 향상도 기대해 볼 수 있게 된다.
2) 점화식
조합의 점화식은 아래와 같다.
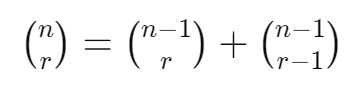
위 점화식의 의미에 대해 간단히 알아보기로 하자. n개의 원소 중 r개의 원소를 선택하는 경우는, 아래의 두 가지 경우로 구분할 수 있다.
- n번째 원소를 포함하지 않고 선택하는 경우
- n번째 원소를 포함하여 선택하는 경우
따라서, 위 두 경우의 수를 더한 경우의 수가 곧 우리가 구하려는 경우의 수가 될 것이다. 각각의 경우에 대해 경우의 수를 구해보자.
① n번째 원소를 포함하지 않고 선택하는 경우
- (n-1)개의 원소 중에서 r개의 원소를 선택하는 경우의 수와 같으므로,
(n-1)Cr이 된다.
② n번째 원소를 포함하여 선택하는 경우
- 이미 n번째 원소는 선택된 상황이므로, (n-1)개의 원소 중 (r-1)개의 원소를 선택하는 경우의 수와 같다. 따라서,
(n-1)C(r-1)이 된다.
이 두 경우의 수를 합하면, 위 점화식이 도출된다. 위 점화식을 조금 더 친숙한 형태로 변환하면, 아래와 같은 형식이 될 것이다.
D[i][j] = D[i-1][j] + D[i-1][j-1]3) 점화식을 활용한 조합 계산
점화식을 활용하여 조합을 계산하는 방법에 대해 알아보자.
① N을 행으로, K를 열로 하는 테이블을 생성한다.
- K는 0부터 시작할 수 있으므로, (N+1) X (N+1) 크기의 테이블을 생성해야 한다.
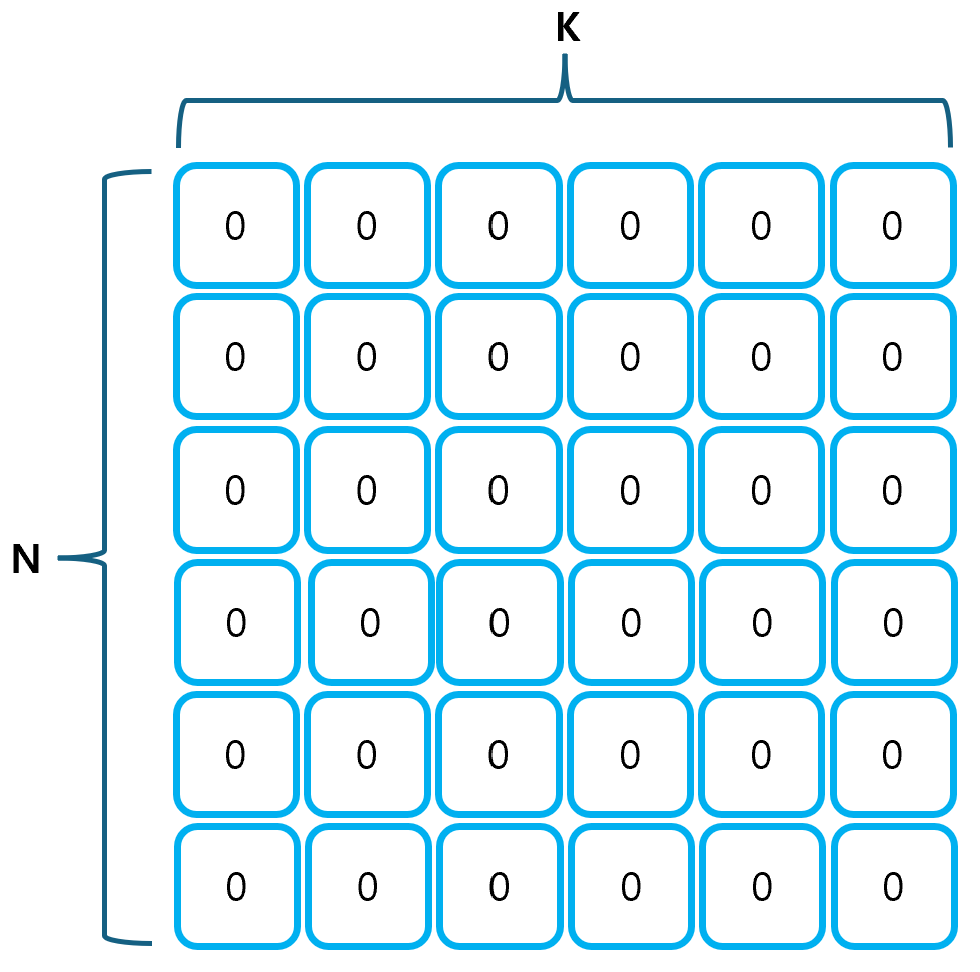
② 생성한 테이블을 초기화한다.
- D[i][0] = 1: 아무 것도 선택하지 않는 경우의 수
- D[i][1] = i: i개 중 1개를 선택하는 경우의 수
- D[i][i] = 1: i개 중 i개를 선택하는 경우의 수
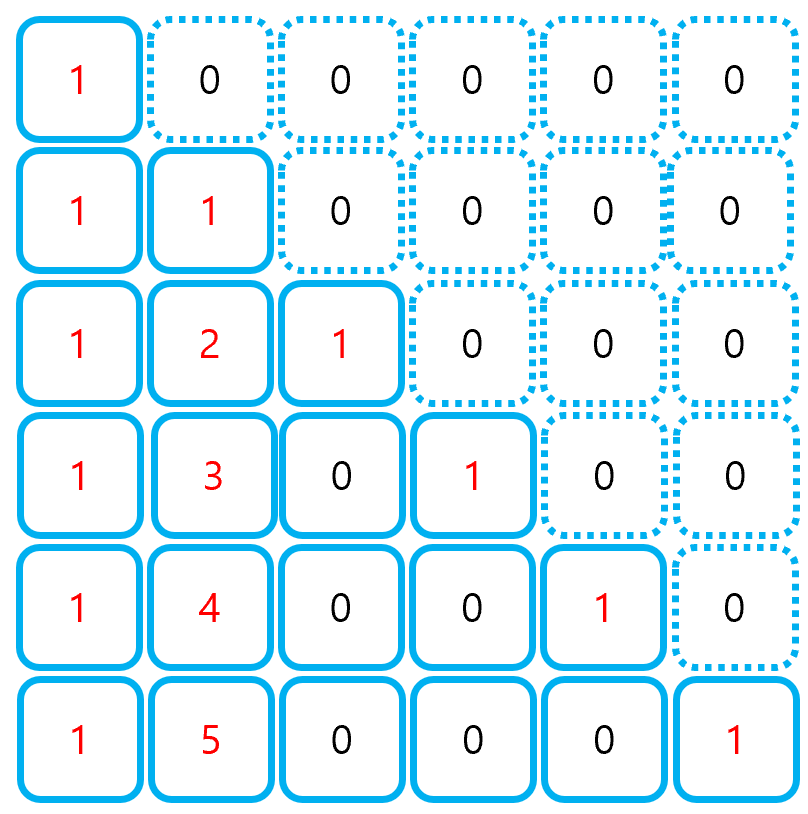
③ 점화식을 이용하여 테이블의 값을 업데이트한다.
- N >= 3인 경우에만 업데이트가 발생한다.
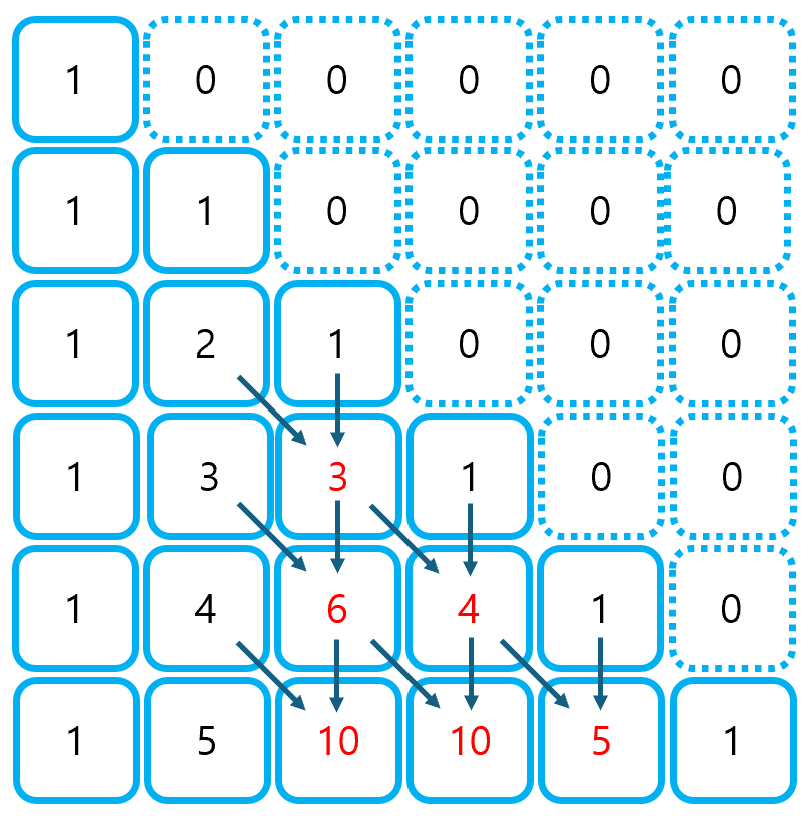
④ D[N][K] 값을 출력한다.
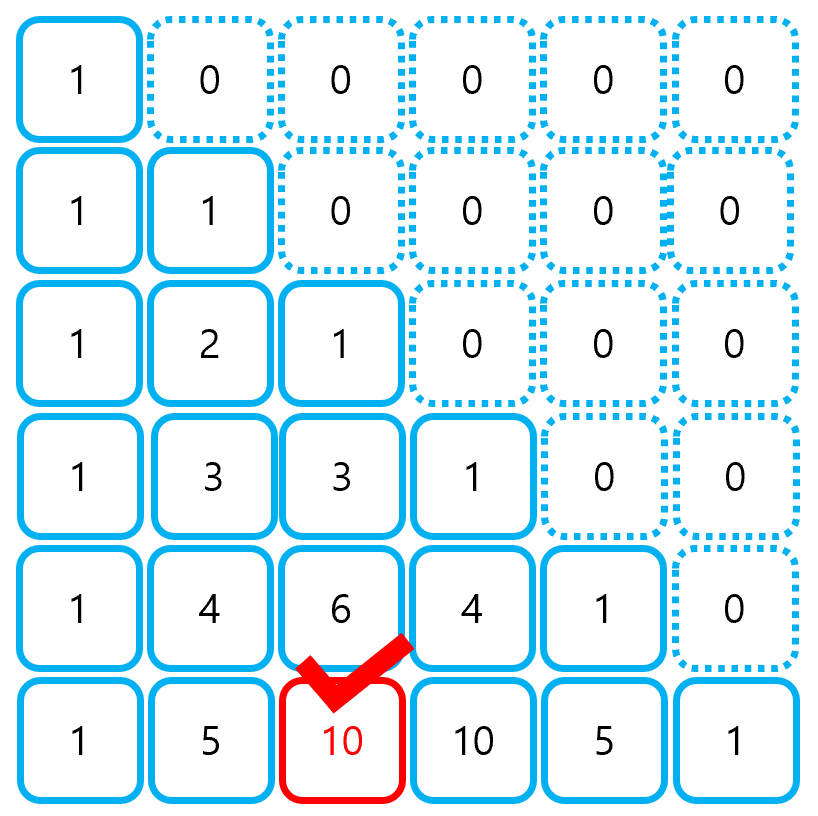
2. 문제 풀이
점화식을 도출해낼 수 있는 역량은 분명 중요하다. 그러나, 이 말이 모든 조합 문제를 점화식을 이용하여 풀이해야 한다는 의미는 아니다. 조합 관련 문제는 어렵게 출제되는 유형이 아니기 때문에, 대부분의 상황에서 math 라이브러리의 comb() 메서드만으로도 풀이가 가능하다. (점화식 도출이 필요한 문제는 다음 포스팅에서 풀이해보기로 하자.)
1) 이항계수 구하기 1
>> 백준 11050번
위와 같이 단순한 문제를 풀이할 때에는 점화식을 활용할 필요가 전혀 없다.
import sys
input = sys.stdin.readline
import math
N, K = map(int, input().split())
result = math.comb(N, K)
print(result)2) 이항계수 구하기 2
>> 백준 11051번
1번 문제와 비슷하지만, N의 범위가 크게 증가하였다. N이 최대 1000인만큼 팩토리얼 계산에 많은 시간이 소요될 것이며, 정수 오버플로의 가능성도 있다.
물론, 질의의 개수가 1개뿐이기 때문에, 시간 초과가 발생할 가능성은 거의 없다. 또한, 파이썬에서는 정수 오버플로를 거의 걱정하지 않아도 되기 때문에, 1번 문제를 풀이할 때 사용한 코드를 그대로 사용해도 아무런 문제가 되지 않는다.
import sys
input = sys.stdin.readline
import math
N, K = map(int, input().split())
result = math.comb(N, K)
print(result % 10007)하지만, 질의의 개수 및 N의 범위가 더 커진다면 시간 초과가 발생할 가능성이 존재하기 때문에, 점화식을 활용하여 조합을 계산하는 방식의 풀이도 연습해보자.
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
# N을 행으로, K를 열로 하는 테이블을 생성한다.
D = [[0 for col in range(N + 1)] for row in range(N + 1)]
# 테이블 초기화
for i in range(N + 1):
D[i][0] = 1
D[i][1] = i
D[i][i] = 1
# 점화식을 이용하여 테이블 값 업데이트
for i in range(3, N + 1): # N >= 3인 경우에만 업데이트 발생
for j in range(1, i): # K는 N보다 클 수 없다.
D[i][j] = D[i-1][j] + D[i-1][j-1]
# 결과 출력
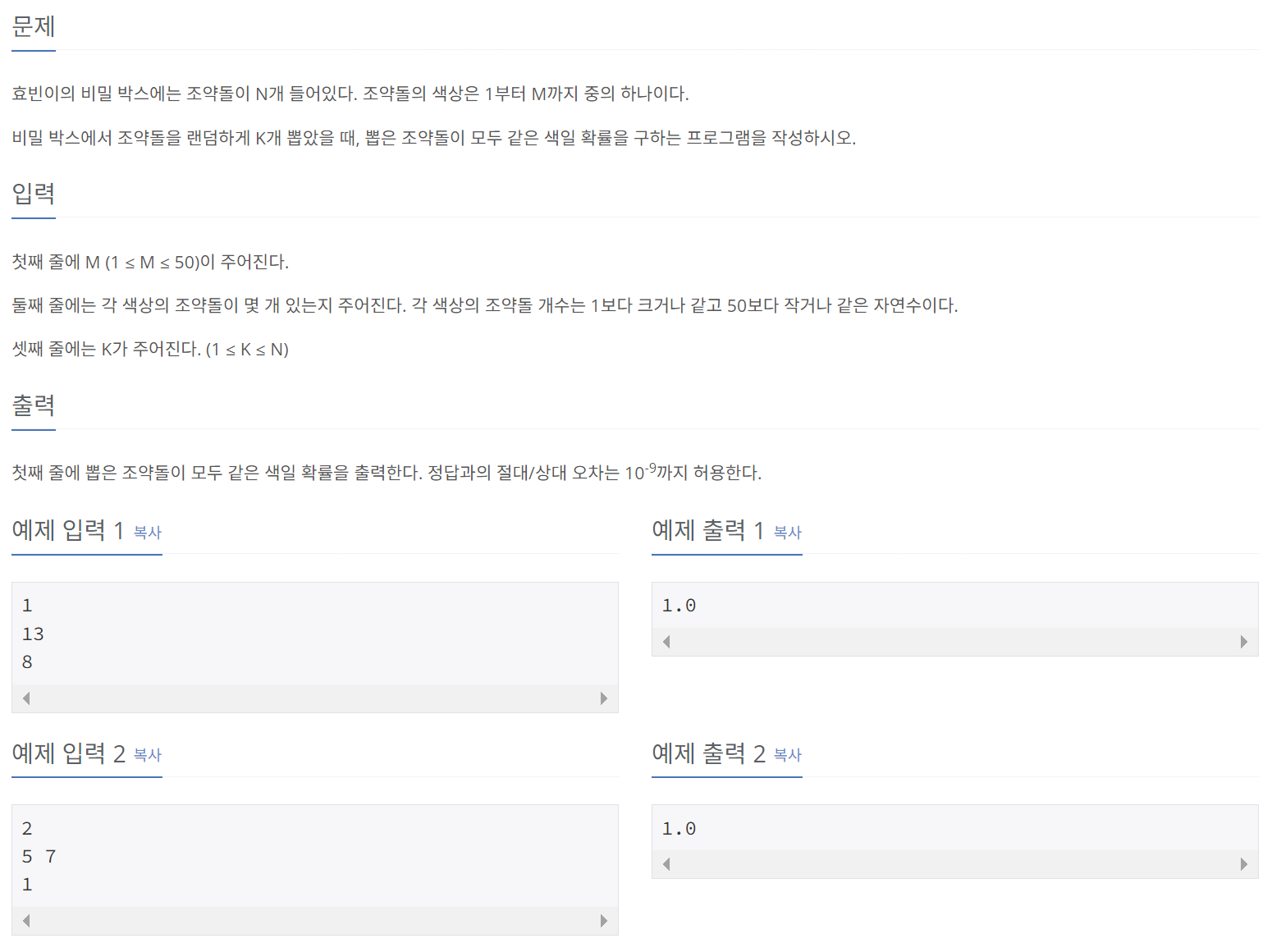
print(D[N][K] % 10007)3) 조약돌 꺼내기
수학 시간에 배웠다시피, 확률을 구하는 방법은 크게 두 가지이다.
- 특정 경우의 수 / 전체 경우의 수
- 연속적인 독립 사건에 대해, 각 사건을 곱사건으로 연결
여기서는 전자의 방식을 사용해야 한다. 즉, 각 조약돌에서 K개를 선택하는 경우의 수를 모두 더한 값을, 전체 조약돌에서 K개를 선택하는 경우의 수로 나누어 확률을 계산할 수 있다.
import sys
input = sys.stdin.readline
import math
M = int(input())
lst = list(map(int, input().split()))
K = int(input())
count = sum(lst) # 전체 조약돌의 수
parent = math.comb(count, K) # 분모 -> 전체 경우의 수
child = 0 # 분자 -> 선택된 조약돌이 모두 같은 색인 경우의 수
for i in lst:
child += math.comb(i, K)
print(child / parent)