1. 백트래킹
1) 개념
백트래킹이란, 가능한 모든 해를 탐색하되, 조건에 맞지 않는 경우 탐색을 중단함으로써, 효율적으로 해를 찾는 알고리즘을 말한다. 백트래킹의 동작 방식을 한 마디로 설명하면 아래와 같다.
Go as deeply as possible, Backtrack if impossible!
백트래킹은 재귀를 사용한다는 점과 그래프를 깊이 우선 탐색한다는 점에서 DFS의 특수한 형태로 볼 수 있다. 하지만 백트래킹은 모든 노드를 탐색하는 DFS와 달리, 조건을 만족하지 않는 경로에 대해선 탐색을 중단(Pruning, 가지치기)한다는 차이점이 있다.
2) 특징
백트래킹은 DFS에 추가할 수 있는 옵션 정도로 생각할 수 있다. 즉, 기존의 DFS 코드에 아래의 로직을 추가하여 백트래킹을 적용할 수 있다.
- 종료 조건(해가 될 수 있는 조건)
- Pruning 조건
- DFS 수행 전에 변경된 사항을 DFS 수행 후에 다시 원상 복구
반드시 위 순서대로 코드에 반영되어야 하며, 일반적으로 종료 조건은 DFS 함수 내에서 가장 먼저 실행되어야 한다. 참고로, Pruning 조건은 특정 조건을 만족하는 경우에 탐색을 중단하는 방식 뿐 아니라, 특정 조건을 만족하는 경우에만 탐색을 진행하는 방식으로 구현할 수도 있다.
3) 백트래킹 적용 기준
일반 DFS로 풀이할 수 있는 문제와 백트래킹까지 적용해야 풀 수 있는 문제를 구분하기 위해선, 특별한 기준이 필요하다. 이 때, 활용할 수 있는 기준은 아래의 두 가지이다.
① 특수 기준
- 사이클이 포함된 그래프에서 노드 간 연결 깊이가 종료 조건인 경우
- Tree - BFS/DFS 포스팅에서 사용했던 백트래킹 적용 기준
② 일반 기준
- Pruning을 적용했을 때, 최적해에 더 빠르게 도달할 수 있는 경우
- 백트래킹의 일반화된 적용 기준
- Pruning을 적용하는 편이 더 유리하다고 판단되면 백트래킹을 적용하고, Pruning을 적용하는 것과 적용하지 않는 것에 큰 차이가 없다고 판단되면 백트래킹을 적용할 필요가 없음을 의미
이번 포스팅에선 일반 기준 백트래킹에 대해 알아보도록 하겠다.
2. 백트래킹 적용 방법
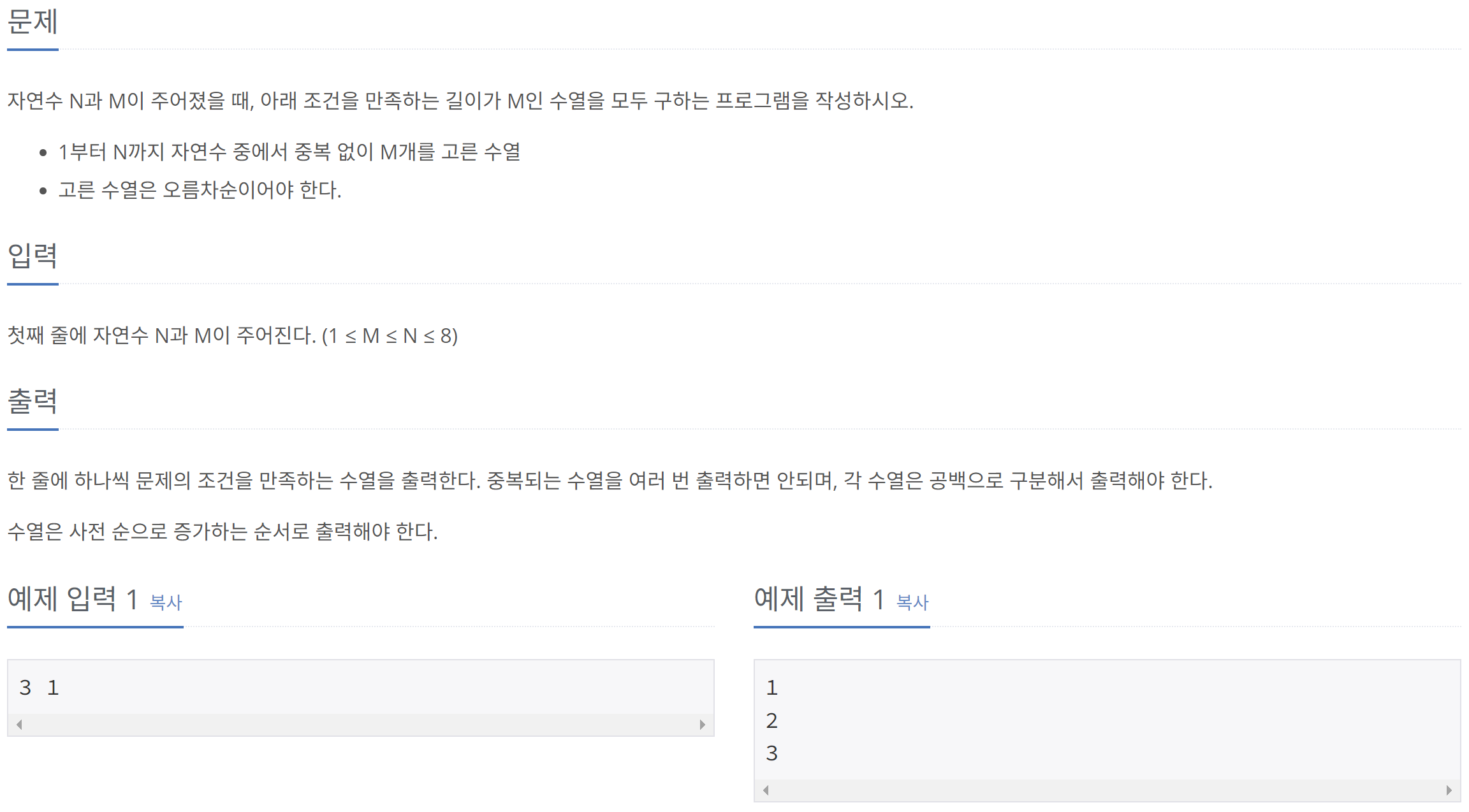
1) N과 M (2)
사실 이 문제는 조합 Iterator를 이용하여 쉽게 풀이할 수 있는 문제이다.
import sys
input = sys.stdin.readline
from itertools import combinations
N, M = map(int, input().split())
# 1부터 N까지의 숫자
lst = [x for x in range(1, N + 1)]
for i in combinations(lst, M): # N개의 숫자 중 M개를 선택하는 경우의 수
print(' '.join(map(str, i)))만약 이 문제를 다른 방식으로 풀어야한다면, 이 문제에 어떻게 접근할 것인가? 이 문제는 연결의 깊이가 M에 도달하는 경우를 찾는 문제이므로, DFS를 이용한 풀이 전략을 떠올릴 수 있을 것이다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 8)
N, M = map(int, input().split())
def dfs(V, answer):
if len(answer) == M: # 종료 조건 설정: M개 선택을 완료한 경우
print(' '.join(map(str, answer)))
return
for i in range(V, N + 1):
dfs(i + 1, answer + [i])
dfs(1, [])위 코드에서 알 수 있다시피, 이 문제는 백트래킹 없이 일반 DFS만으로 풀이할 수 있다. 그 이유가 무엇일까? 예를 들어, [1, 2, 3, 4] 중 3개의 숫자를 선택해야 하는 상황을 생각해보자. 만약 1에서 4로 이동할 경우, 오름차순을 만족하는 세번째 숫자를 선택할 방법이 없다. 따라서, 이러한 경우에 대해 탐색을 중단할 수 있도록 Pruning을 적용할 수 있을 것이다.
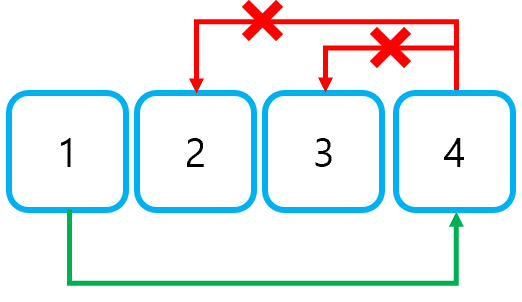
하지만 잘 생각해보면, 굳이 백트래킹을 적용하지 않아도 4를 선택한 순간 DFS(4)에 의해 DFS(5)가 호출되고, DFS(5)는 for문의 range 조건에 의해 아무 것도 실행하지 않고 종료되기 때문에, Pruning을 적용하는 것과 적용하지 않는 것에 큰 차이가 없다. 따라서, 이러한 문제는 백트래킹을 적용하지 않은 일반 DFS만으로 풀이해도 충분하다.
물론, 백트래킹을 적용하여 풀이하는 것도 가능하다. 어떠한 전략을 선택하든 큰 상관은 없으나, 개인적으로는 코드가 간결한 일반 DFS를 사용할 것을 권장한다. 백트래킹을 적용한 코드는 아래와 같다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 8)
N, M = map(int, input().split())
visited = [0] * (N + 1)
def dfs(V, answer):
if len(answer) == M: # 종료 조건 설정: M개 선택을 완료한 경우
print(' '.join(map(str, answer)))
return
for i in range(V, N + 1):
if visited[i] == 0:
visited[i] = 1 # dfs 수행 전에 변경된 사항 1
answer.append(i) # dfs 수행 전에 변경된 사항 2
dfs(i + 1, answer)
visited[i] = 0 # dfs 수행 후에 다시 원상 복구
answer.pop() # dfs 수행 후에 다시 원상 복구
dfs(1, [])참고로, 위 문제는 오름차순으로만 탐색하기 때문에, visited 배열을 사용하지 않아도 되지만, 조금 더 일반적인 백트래킹 코드를 작성하기 위해 사용하였다. 또한, Pruning 조건이 명시되지 않은 것을 확인할 수 있는데, 이와 같이 일반 조건 백트래킹에서 Pruning 조건이 명시되지 않은 경우, 일반 DFS로 바꾸어 풀이할 수 있다.
실제 실행 시간을 확인해봐도, 백트래킹을 적용한 것과 적용하지 않은 것에 큰 차이가 없음을 확인할 수 있다.

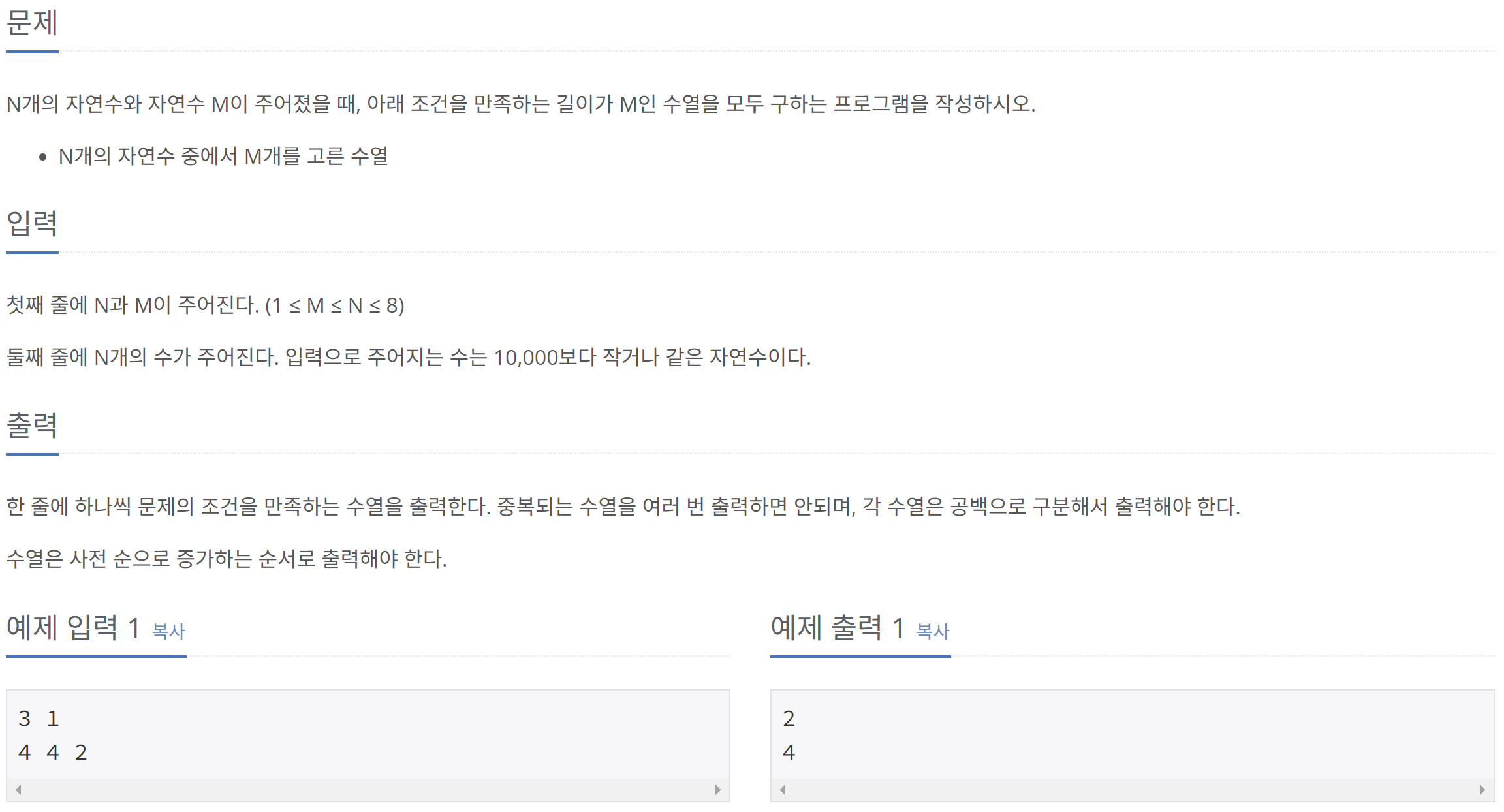
2) N과 M (9)
백트래킹이 어느 정도 이해되었다면, 이와 비슷한 다른 문제도 풀어보자.
사실 이 문제도 순열 Iterator를 이용하여 쉽게 풀이할 수 있는 문제이다.
import sys
input = sys.stdin.readline
from itertools import permutations
N, M = map(int, input().split())
lst = list(map(int, input().split()))
# 순열 생성 후 중복을 제거
perms = set(permutations(lst, M))
for i in sorted(perms):
print(' '.join(map(str, i)))그러나 이번에도 Iterator가 아닌, DFS로 이 문제에 접근해보자. 미리 이야기하자면, 이 문제를 일반 DFS로 풀이할 경우, 시간 초과가 발생할 가능성이 매우 높다.
예를 들어 [1, 1, 1, 1, 1, 1, 2]의 배열에서 2개를 골라 수열을 만드는 경우를 생각해보자. 가능한 경우의 수는 (1, 1), (1, 2), (2, 1)의 세 가지 밖에 없지만, 반복되는 1에 의해 매번 똑같은 수열을 생성하는 데에 많은 시간을 낭비하게 된다.
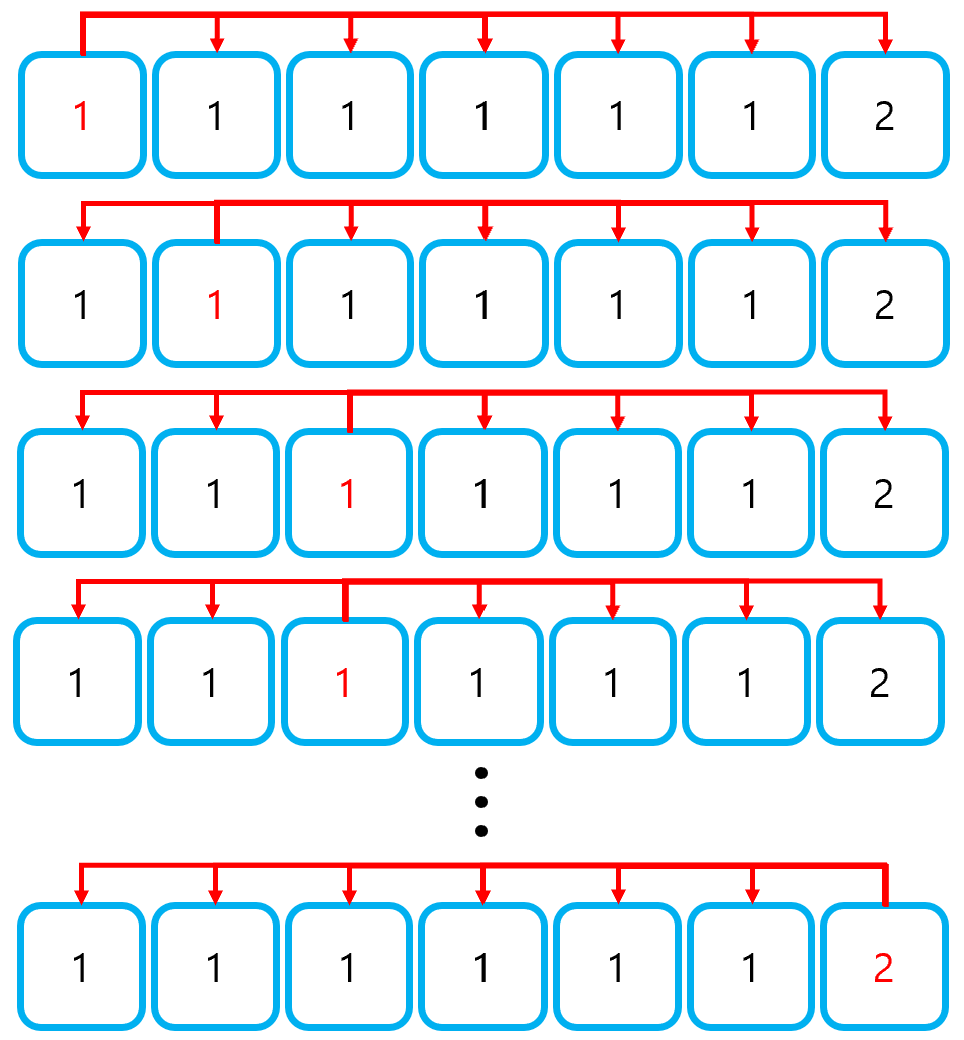
따라서 중복된 결과를 만드는 경우에 대해 반드시 Pruning을 적용해주어야 한다. 즉, 중복된 결과를 만드는 조건에 대해 탐색을 중단하는 로직(Pruning 조건)을 추가해주어야 한다는 것이다. 정렬된 리스트를 기준으로 중복이 발생하는 상황은, 아래의 두 조건을 만족하는 경우이다.
- 어떤 원소가 바로 앞 원소와 동일한 경우
- 바로 앞 원소에 아직 방문하지 않은 경우
위 두 조건을 모두 만족할 경우, 바로 앞 원소에 의해 만들어지는 결과와 동일할 것이 자명하므로, 탐색을 중단해야 한다. 즉, 중복되기 전 최초의 원소에 대해서만 DFS 탐색을 수행하고, 그 이후에 나오는 중복 원소에 대해서는 탐색을 수행하지 않겠다는 의미이다. 이제 이 내용을 바탕으로 문제를 풀어보자.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 8)
N, M = map(int, input().split())
lst = list(map(int, input().split()))
lst.sort() # 중복 여부를 확인하기 위해 리스트를 정렬
result = []
visited = [0] * N
def dfs(answer):
if len(answer) == M: # 조건을 만족하는 해 (종료 조건)
result.append(' '.join(map(str, answer)))
return
for i in range(N):
if visited[i] == 0:
# Pruning 조건
if i > 0 and lst[i] == lst[i-1] and visited[i-1] == 0:
continue # Pruning
visited[i] = 1 # dfs 수행 전에 변경된 사항 1
answer.append(lst[i]) # dfs 수행 전에 변경된 사항 2
dfs(answer)
visited[i] = 0 # dfs 수행 후에 다시 원상 복구
answer.pop() # dfs 수행 후에 다시 원상 복구
dfs([])
for i in result:
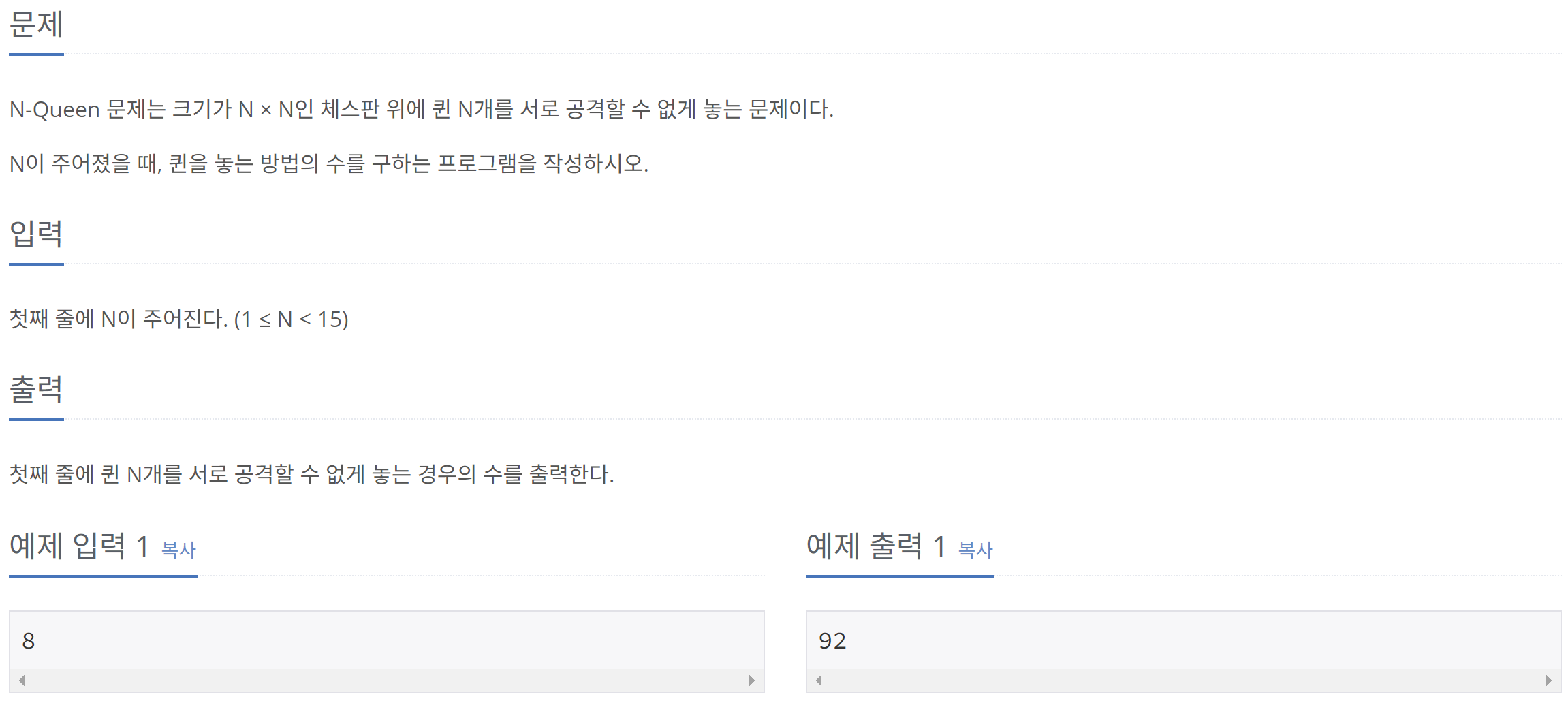
print(i)3. N-Queen Problem
1) 개념
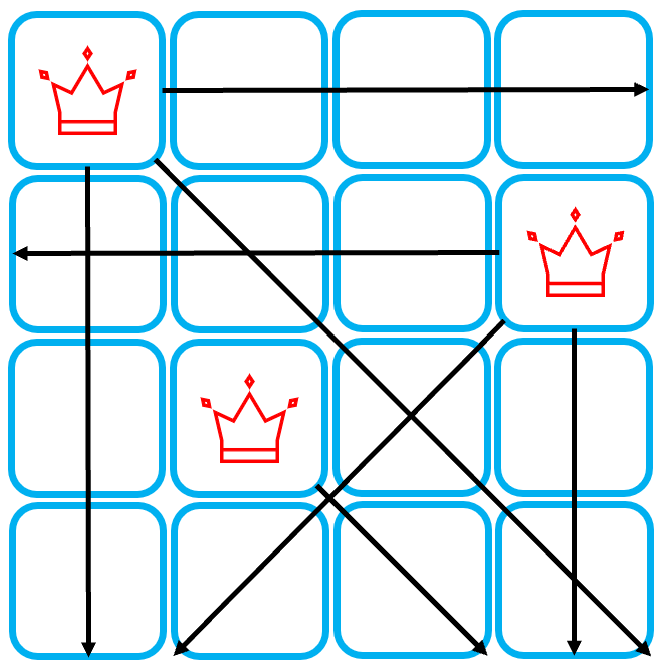
N-Queen Problem은 백트래킹을 이용한 대표적인 문제 중 하나이다. 여기서 N-Queen Problem이란, N X N 크기의 체스 판에 상하좌우, 대각선 방향으로 이동할 수 있는 N개의 Queen을 서로 잡을 수 없도록 놓는 방법을 찾는 문제를 말한다.
이 문제의 기본적인 접근법은 Queen을 각 행에 하나씩 배치하되, 다른 Queen과 동일한 열 또는, 대각선 상에 위치되는 경우에 대해 Pruning을 적용하는 것이다. 아래의 예시를 보자.
N = 4라고 가정하고, 첫번째 Queen을 첫행 첫열에 위치시켜보자.

이 때, 두번째 Queen이 위치할 수 있는 경우는 아래의 두 가지 뿐이다.
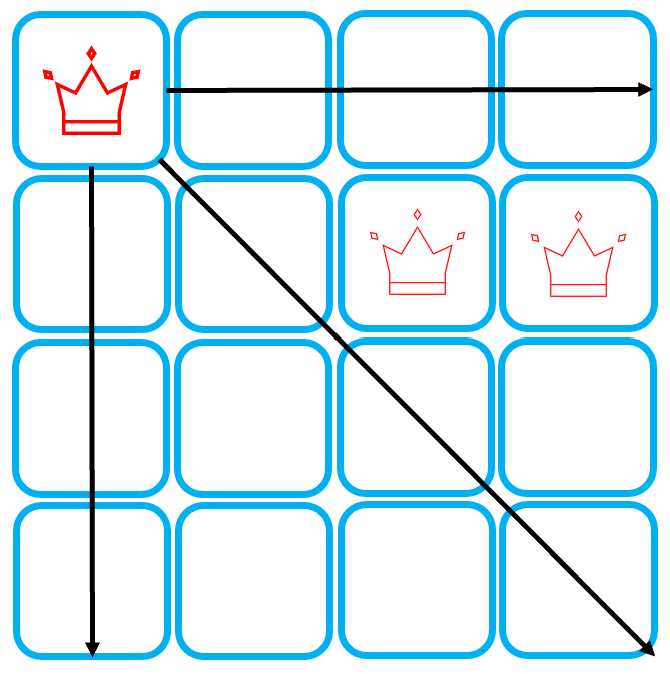
두 자리 중 왼쪽 자리를 선택해보기로 하자.
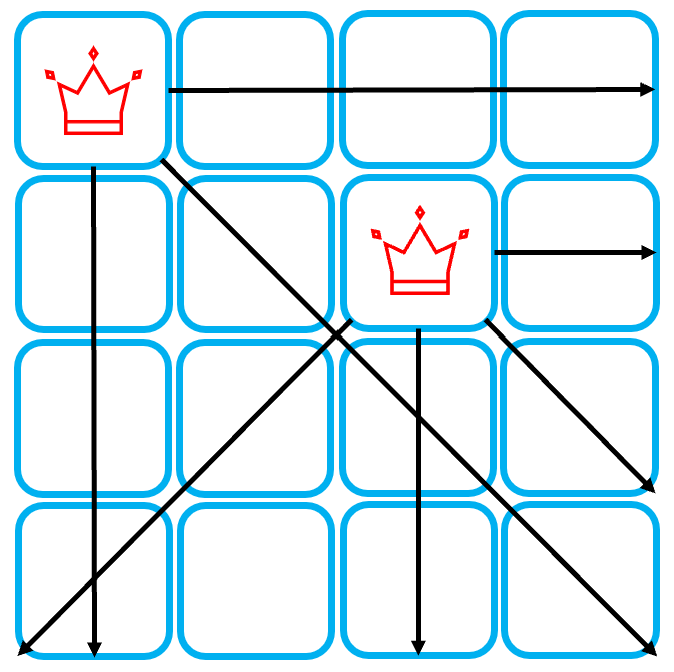
세번째 행에 Queen을 둘 수 없으므로, 탐색을 중단해야 한다. 다시 이전 단계로 돌아가 오른쪽 자리를 선택해보자.
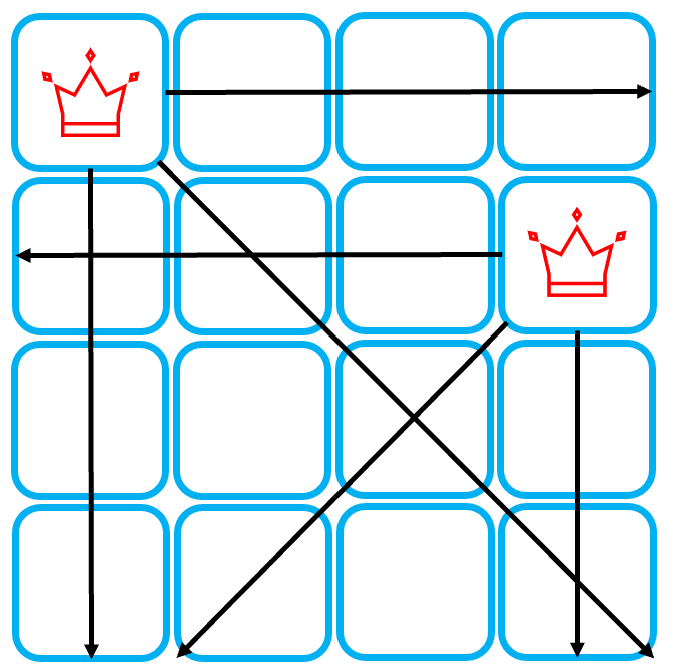
다행히 이번에는 세번째 Queen을 놓을 수 있는 자리가 생겼다.
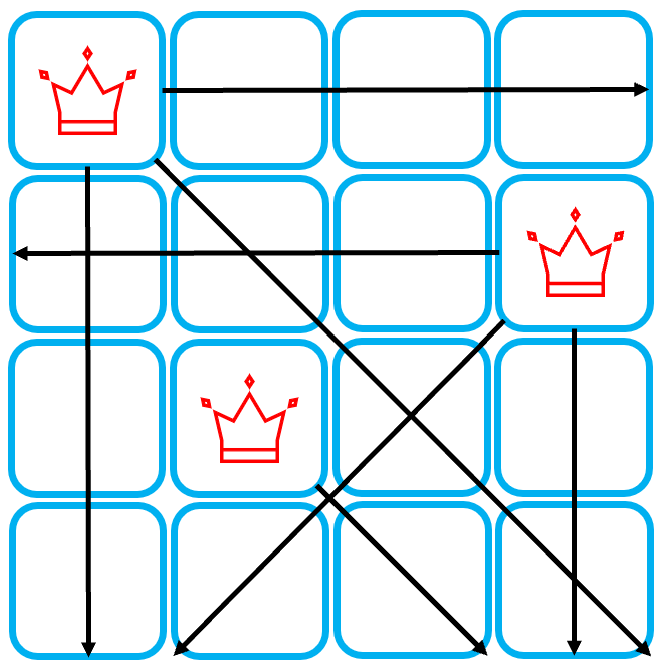
하지만, 이 자리에 세번째 Queen을 위치시키는 순간, 네번째 Queen을 놓을 수 없게 된다. 따라서, 이러한 경우에 대해서도 탐색을 중단하고, 첫번째 Queen을 1행 2열로 옮기는 경우부터 다시 시작해야 할 것이다. (이후 과정은 생략한다.)
이와 같은 방식으로 탐색을 진행하다가, 종료 조건(N개의 Queen을 성공적으로 배치)에 도달할 때마다, 결과 값을 1씩 증가시켜 전체 경우의 수를 계산한다.
2) 문제 풀이
N-Queen Problem을 풀 때에는, 체스판 전체를 저장할 필요 없이 Queen의 위치만 저장하면 되기 때문에 2차원 배열이 아닌 1차원 배열을 사용한다. 이 때, 1차원 배열의 Index는 Queen이 위치한 Row를, Element는 Queen이 위치한 Column을 의미하게 된다. 또한, 대각성 상에 위치하는 경우는 두 위치의 가로 길이 차이와 세로 길이 차이가 동일한지 여부로 확인할 수 있다.
import sys
input = sys.stdin.readline
N = int(input())
queens = [0] * N # 퀸이 배치된 위치
cnt = 0 # N개의 Queen을 배치할 수 있는 경우의 수
def dfs(row):
global cnt
if row == N: # 종료 조건
cnt += 1
return
for col in range(N):
queens[row] = col # 한 행에 포함된 모든 열에 대해 Queen을 놓음
if is_avaliable(row): # Pruning 조건
dfs(row + 1) # 현재 Row에서 available한 모든 Col에 대해 다음 행에 대한 DFS를 수행
def is_avaliable(row): # 위의 queens[row] = col이 가능한지 여부를 검사
for i in range(row): # row 이전의 모든 행에 대해 현재 퀸과 동일한 열을 갖거나, 대각선 상에 위치한 경우가 있으면 False를 반환
if queens[row] == queens[i] or abs(queens[row] - queens[i]) == row - i:
return False
return True
dfs(0)
print(cnt)이 문제는 특이하게도 sys.setrecursionlimit(10 ** 8)을 붙이면, 시간 초과가 발생한다. 정확한 이유는 알 수 없지만, 백트래킹이 적용된 코드인만큼 재귀 깊이 제한을 설정하지 않는 편이 좋을 것 같다. 참고로, Python3로는 시간 초과가 발생하므로, PyPy3로 제출해야 한다.
또 한 가지 주의해야 할 것은 row는 0부터 시작하지만, 종료 조건은 row == N이 되어야 한다는 것이다. 그 이유는 DFS(N)에서 탐색이 종료되기 때문이다. 백트래킹의 종료 조건을 설정할 때, 반드시 유의해야 할 부분이다.