분할 정복법

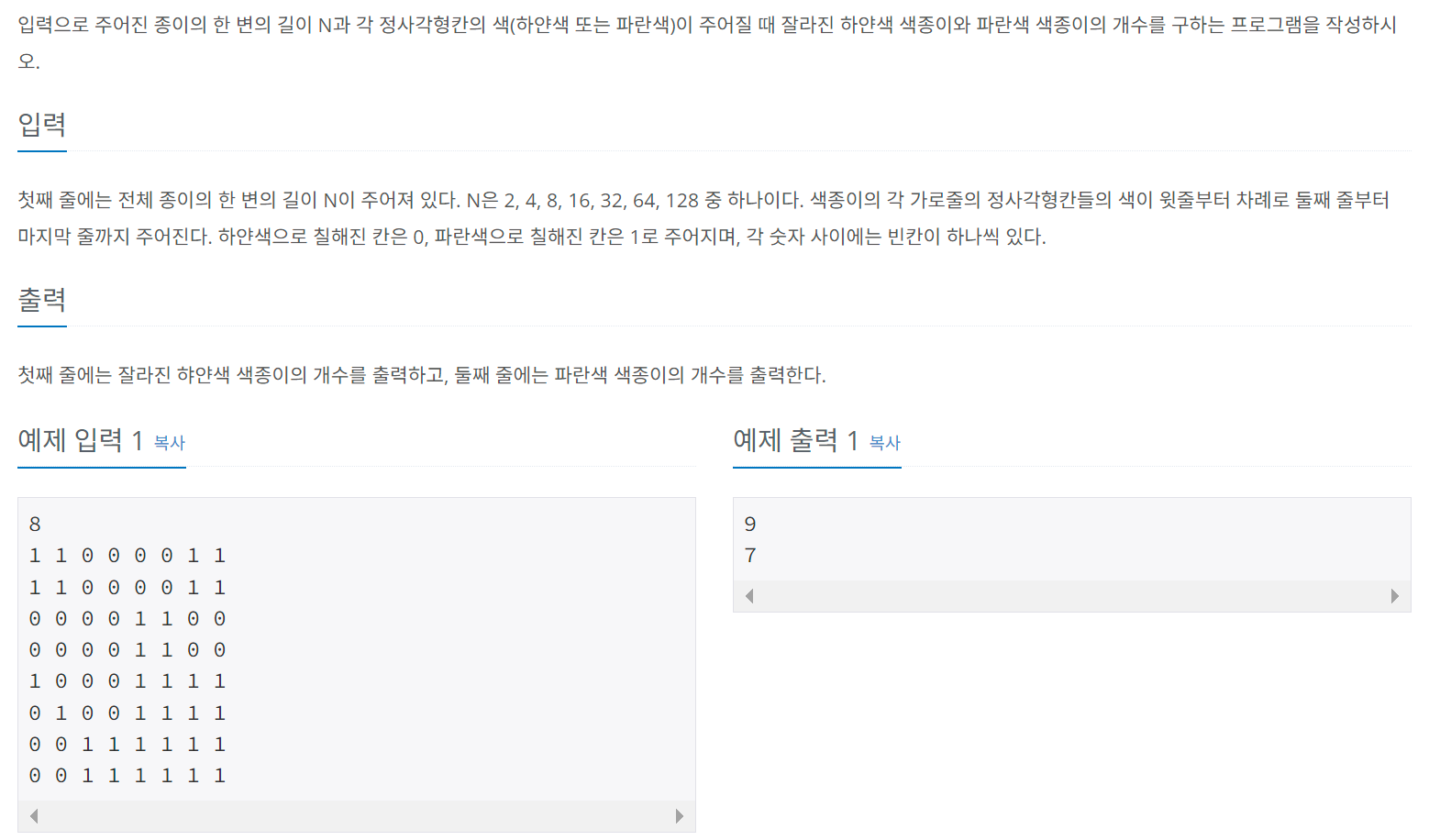
1. 분할 정복법

분할 정복은 큰 문제를 작은 문제로 분할하여 해결한 후, 해결 결과를 차례로 병합해나가며 전체 문제의 해답을 알아내는 설계 전략이다.

① 문제 패턴

• 분할 정복을 활용하는 문제의 패턴은 대부분 정형화되어 있기 때문에, 분할 정복을 활용하는 문제라는 사실은 어렵지 않게 파악할 수 있다.
• 대표적인 패턴은 아래와 같다.
  • N의 크기는 반드시 분할하는 횟수의 배수가 된다.
  • 조건을 만족할 때까지 종이 접기(또는 종이 자르기)를 반복 수행한다.

② 구현 상 특징

• 재귀 호출 또는 while 문으로 구현한다.
• row, column, N(행렬의 가로/세로 길이)을 사용하여, 연산 범위를 결정한다.

def divide(row, col, size):
    for i in range(row, row + size):
        for j in range(col, col + size):
        
        	if ... # 특정 조건을 만족할 때까지 3등분
              divide(row, col, size // 3)
              divide(row, col + size // 3, size // 3)
              divide(row, col + 2 * size // 3, size // 3)

              divide(row + size // 3, col, size // 3)
              divide(row + size // 3, col + size // 3, size // 3)
              divide(row + size // 3, col + 2 * size // 3, size // 3)

              divide(row + 2 * size // 3, col, size // 3)
              divide(row + 2 * size // 3, col + size // 3, size // 3)
              divide(row + 2 * size // 3, col + 2 * size // 3, size // 3)
              
              return
           ...

③ 재귀 호출과 while 문 구분

• 분할된 Subproblem을 모두 활용하여 전체 문제의 해답을 알아내는 문제는 재귀 호출로 구현한다.
• 분할된 Subproblem 중 유효한 Subproblem을 반복적으로 선택하여 전체 문제의 해답을 알아내는 문제는 while 문으로 구현한다.

자세한 내용은 직접 문제를 풀어보면서 이해해보기로 하자.

2. 문제 풀이

1) 색종이 만들기

>> 백준 2630번

위 문제를 풀이하는 기본적인 전략은, 한 가지 색상으로만 이루어질 때까지 정사각형을 4등분한 후, 분할이 완료되었을 때에 존재하는 하얀색 색종이와 파란색 색종이의 개수를 구하는 것이다. 즉, 분할 결과가 한 가지 색상으로만 이루어져 있는 경우는 해결된 문제로 보고, 그렇지 않은 경우는 해결되어야 할 부분 문제로 간주하여 풀이할 수 있는 것이다.

당연히, 전체 문제의 해답을 얻기 위해선 분할된 Subproblem을 모두 활용해야 하므로, 재귀 호출을 활용하여 구현해야 한다.

import sys
input = sys.stdin.readline

N = int(input())
paper = [list(map(int, input().split())) for i in range(N)] # N × N 사이즈의 종이

white = 0 # 흰색 종이의 개수
blue = 0 # 파란색 종이의 개수

def divide(i, j, n):
    color = paper[i][j] # 시작점의 색깔
    global blue
    global white

    for k in range(i, i + n):
        for l in range(j, j + n):
            if paper[k][l] != color: # 시작점의 색깔과 하나라도 다른 색이 발견될 경우 4등분을 수행함
                divide(i, j, n // 2) # 1사분면
                divide(i + n // 2, j, n // 2) # 2사분면
                divide(i, j + n // 2, n // 2) # 3사분면
                divide(i + n // 2, j + n // 2, n // 2) # 4사분면
                return # 조건을 만족하지 않는 경우에 대해서는 아래의 로직이 실행되지 않도록 함수를 종료시킴

    if color == 0: # 흰색으로만 구성된 경우
        white += 1
    else: # 파란색으로만 구성된 경우
        blue += 1

divide(0, 0, N)

print(white)
print(blue)

2) Z 방향으로 순회하기

>> 백준 1074번

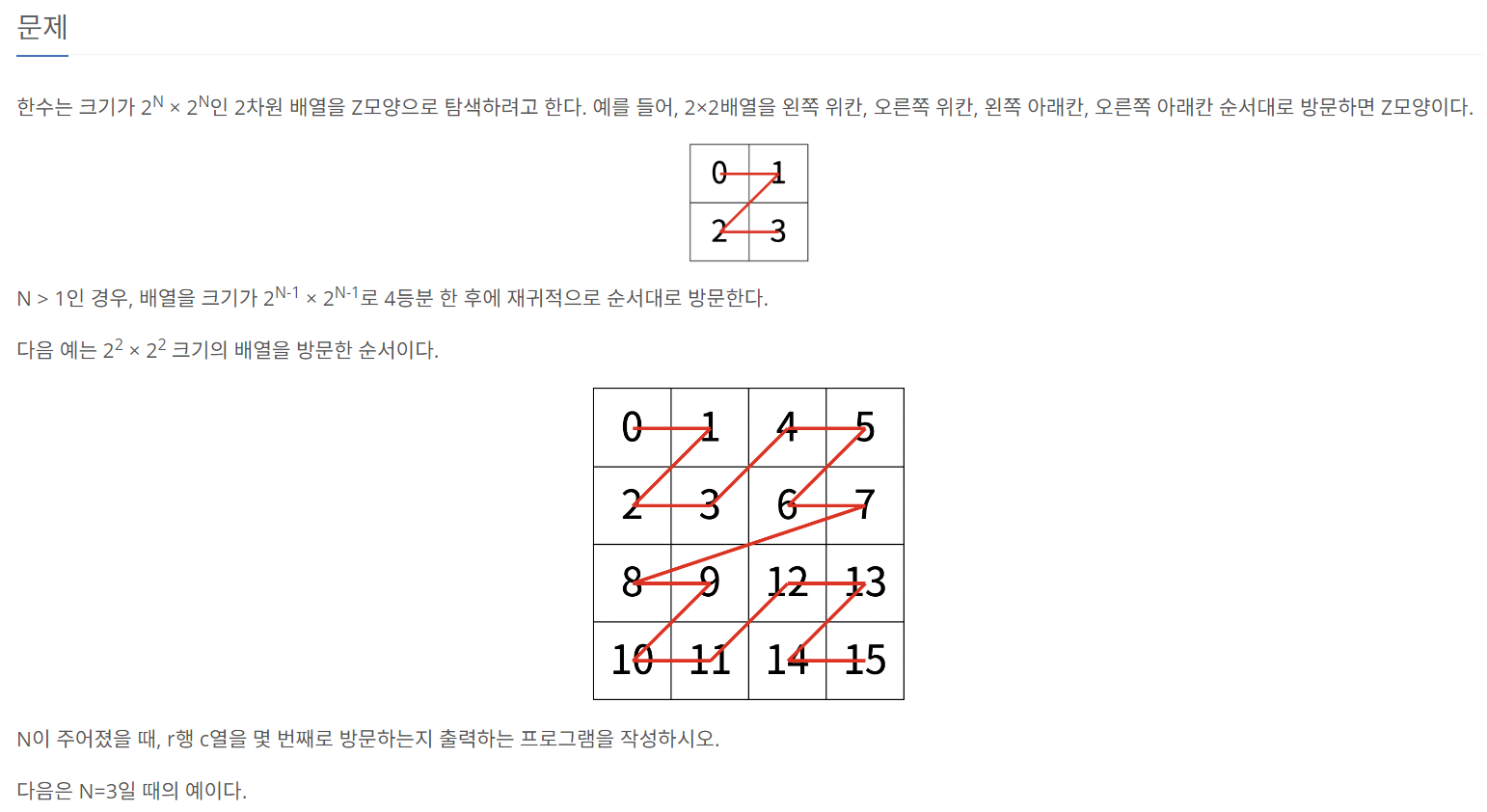
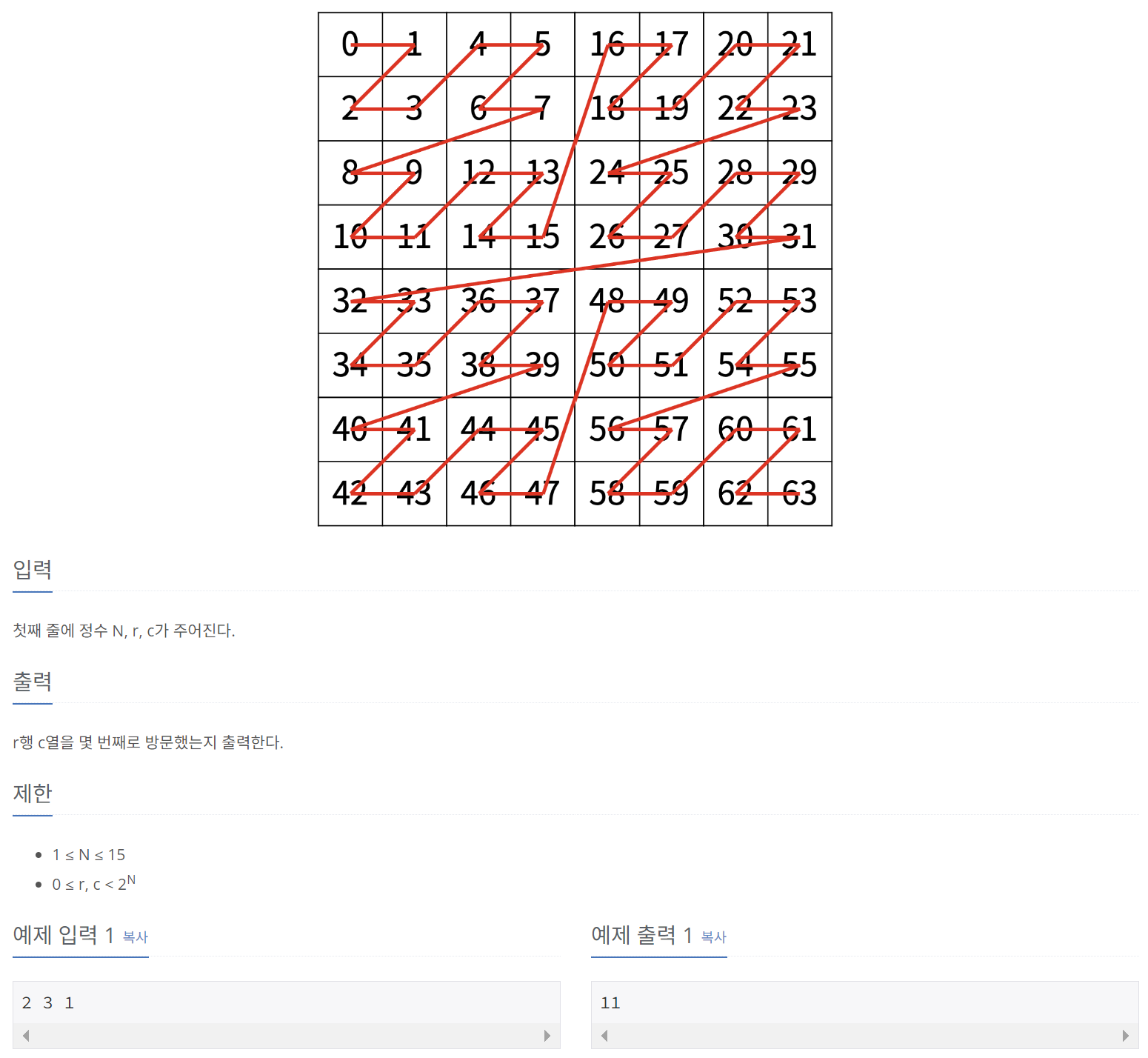
N의 최대 값이 15이므로, 직접 배열을 생성하는 방식으로는 풀이할 수 없을 것 같다. 이 문제 역시 분할 정복법을 사용하여 풀이할 수 있는데, 해결 전략은 아래와 같다.

• r과 c의 값과 배열 전체 크기의 절반(half)을 비교하면, r행 c열이 몇번째 사분면에 속하는지 알아낼 수 있다.
  
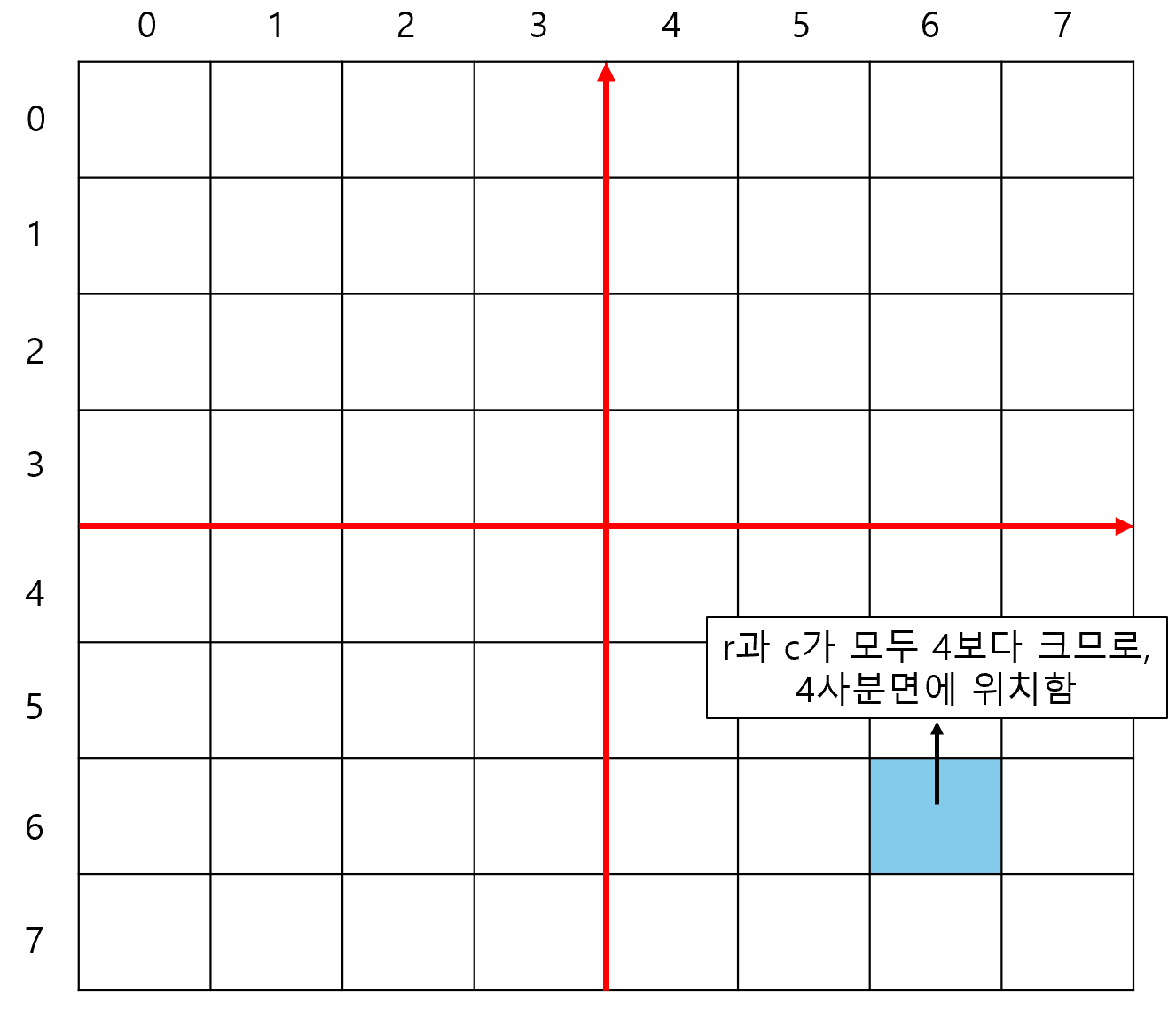
• 만약 r행 c열이 4사분면에 위치한다면, 방문 횟수는 최소 half * half * 3보다 크다.
• 이제 r행 c열이 위치한 4사분면을 기준으로, 다시 위 과정을 반복한다. 이 때, 기존 4사분면의 첫 행과 열이 0이 되도록 조정해야 하므로, r과 c의 값에서 half만큼을 빼주어야 한다.
  
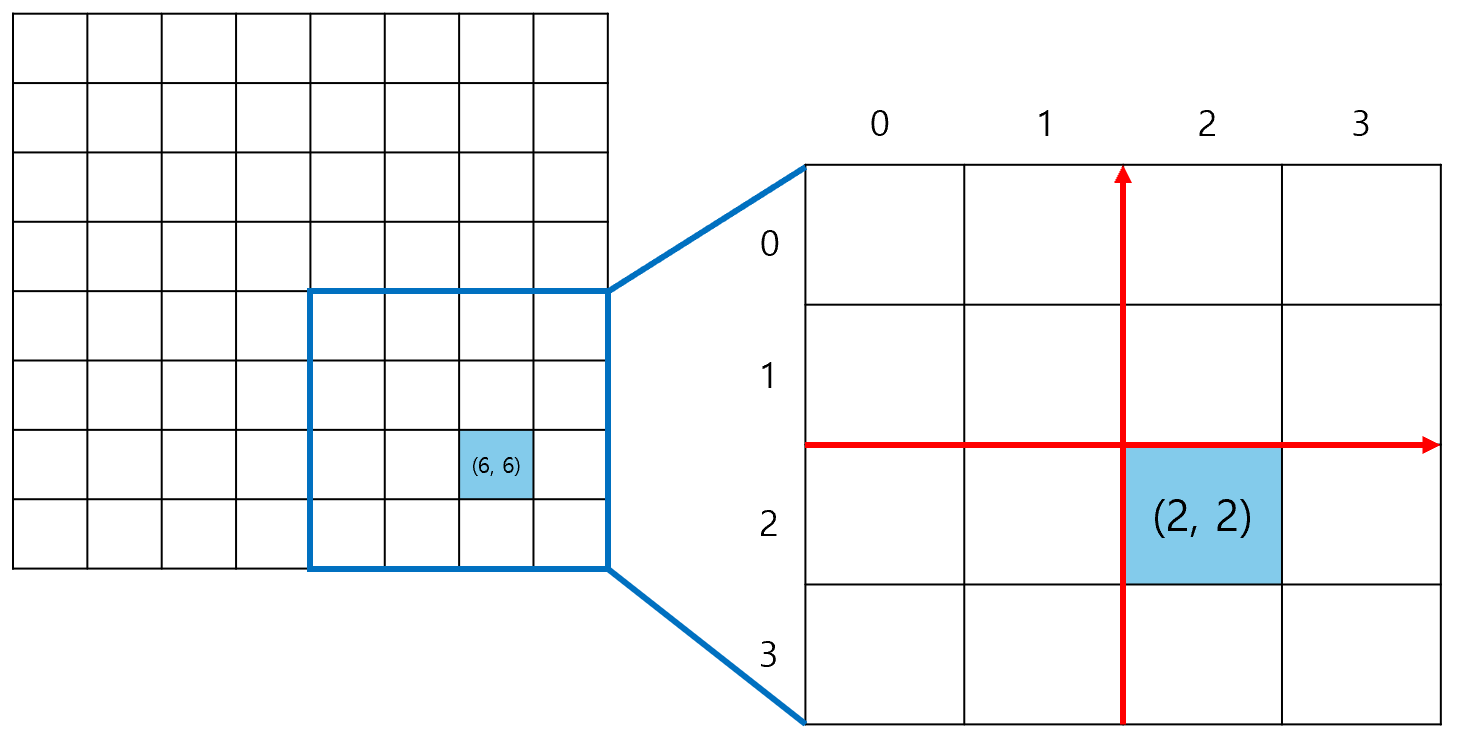
• half 값을 조정된 배열의 절반 크기로 조정한다. 이번에도, r행 c열이 4사분면에 위치하므로, 방문 횟수에 half * half * 3을 더한다.
• 위 과정을 N이 0이 될 때까지 반복한다.

즉, 배열을 더 이상 4등분할 수 없을 때까지 분할하여 해답을 찾는, 전형적인 분할 정복 문제인 것이다. 이 문제는 분할된 Subproblem 중 유효한 Subproblem을 반복적으로 선택하여 전체 문제의 해답을 알아내는 문제이므로, while 문으로 풀이한다.

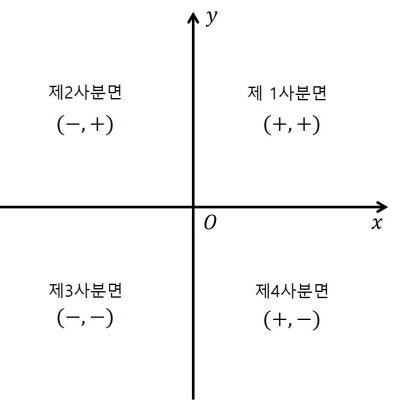
(아래의 코드에서 각 사분면이 어디를 의미하는지에 대해서는 아래의 이미지를 참고하라.)

import sys
input = sys.stdin.readline

N, r, c = map(int, input().split())
answer = 0  

while N != 0:
    N -= 1
    half = 2 ** N # 기준 배열의 절반 크기

    if r < half and c >= half: # 1사분면
        answer += half ** 2 # 2사분면의 크기만큼을 더함
        c -= half # 현재의 1사분면을 기준 배열로 변경

    elif r < half and c < half: # 2사분면
        pass # 아무 로직도 수행하지 않아도 됨.

    elif r >= half and c < half: # 3사분면
        answer += (half ** 2) * 2 # 1사분면, 2사분면의 크기만큼을 더함
        r -= half # 현재의 3사분면을 기준 배열로 변경

    else: # 4사분면
        answer += (half ** 2) * 3 # 1사분면, 2사분면, 3사분면의 크기만큼을 더함
        c -= half # 현재의 4사분면을 기준 배열로 변경
        r -= half # 현재의 4사분면을 기준 배열로 변경

print(answer)