1. 최소 공통 조상
최소 공통 조상(Lowest Common Ancestor, LCA) 알고리즘은 말 그대로, 트리에서 임의의 두 노드를 선택했을 때, 두 노드의 첫 공통 부모(조상)가 되는 노드를 찾는 방법이다. 아래와 같은 트리가 있다고 하자. (참고로, 꼭 이진 트리가 아니어도 트리의 형식만 갖추고 있으면, LCA 알고리즘을 사용할 수 있다.)
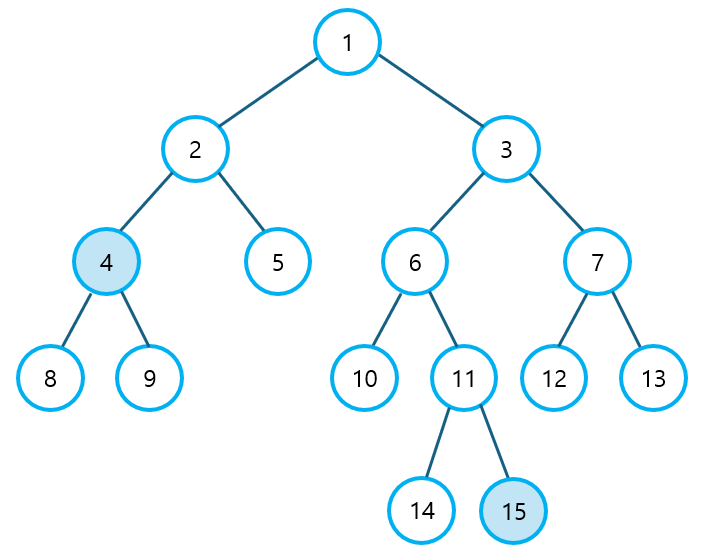
위의 트리에서 4번과 15번 노드의 최소 공통 조상을 찾아보자.
1) LCA 알고리즘
① DFS 탐색을 통해 각 노드의 부모 노드와 깊이를 저장한다.

② 선택된 두 노드의 깊이가 다를 경우, 깊이가 같아질 때까지 부모 노드로 이동한다.
- 만약 두 노드가 같아질 경우, 해당 노드가 최소 공통 조상이 된다.
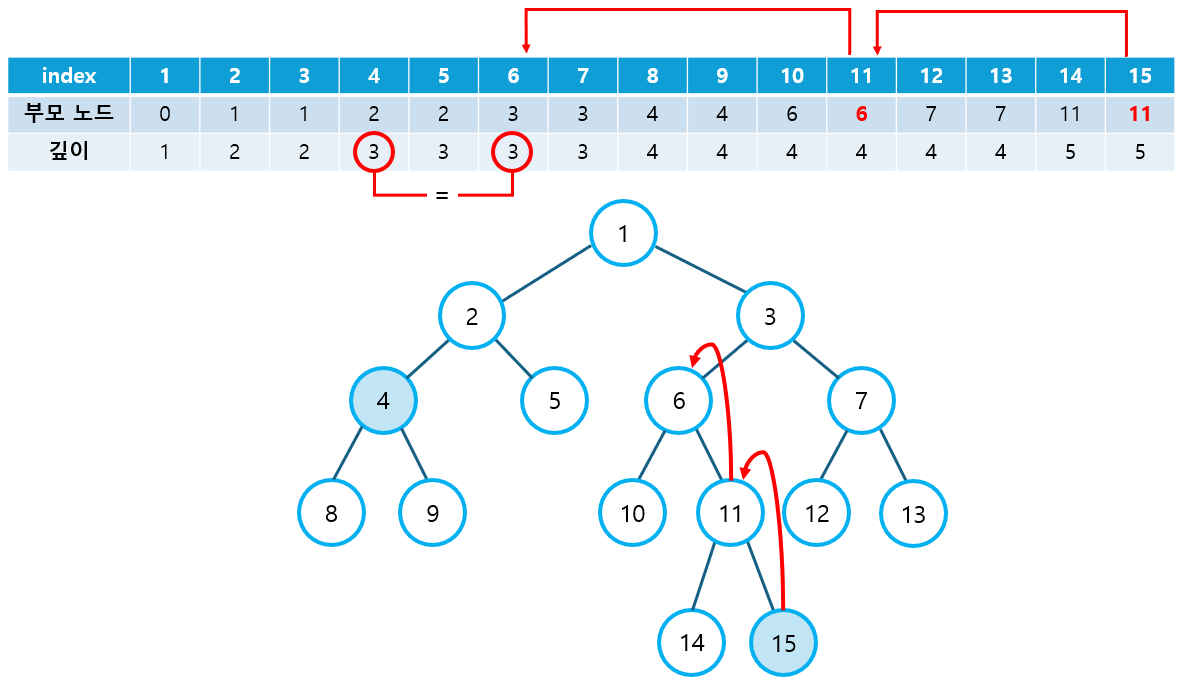
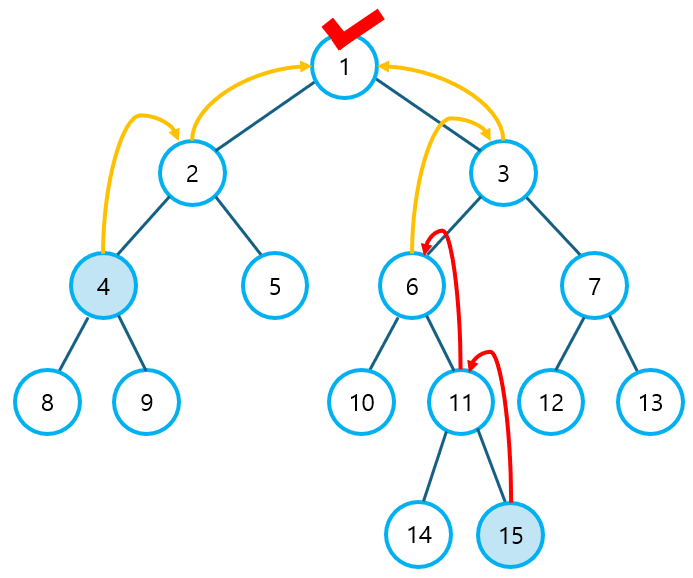
③ 깊이가 같아진 상태에서는 두 노드 모두 부모 노드로 이동한다.
- 두 노드가 같아질 때까지 해당 과정을 반복한다. 이 때, 처음으로 만나게 되는 노드가 최소 공통 조상이 된다.
2) 개선된 LCA 알고리즘
물론 위와 같은 방식으로도 최소 공통 조상을 찾아낼 수는 있지만, 시간 복잡도가 높다는 문제가 있다. 트리의 깊이를 N이라 할 때, 최소 공통 조상을 찾기 위한 시간 복잡도는 최악의 경우 O(N)이 된다.
이 때, 동적 계획법을 활용하여 시간 복잡도를 O(log N)으로 개선할 수 있다. LCA를 더욱 빠르게 만드는 핵심 원리는, 기존에 한 단계씩 부모로 올라가던 방식을, 한번에 2 ^ K번째 부모 노드로 올라가는 방식으로 변경하는 것이다. 자세한 내용을 설명하면 아래와 같다. (편의상 부모 노드를 첫번째 부모 노드, 부모의 부모 노드를 두번째 부모 노드라 칭하기로 한다.)
① 각 노드의 2 ^ K(= 0, 1, 2, ...)번째 부모 노드를 저장한다.
- N번 노드의 K번째 부모를 나타내는 점화식은
P[K][N] = P[K-1][P[K-1][N]]이 된다. - 예시: N번 노드의 네번째(K = 2) 부모 노드는 N번 노드의 두번째(K = 1) 부모 노드의 두번째 부모 노드이다.
② K 값은 트리의 깊이 ≥ 2 ^ K를 만족하는 최대 값으로 결정된다.
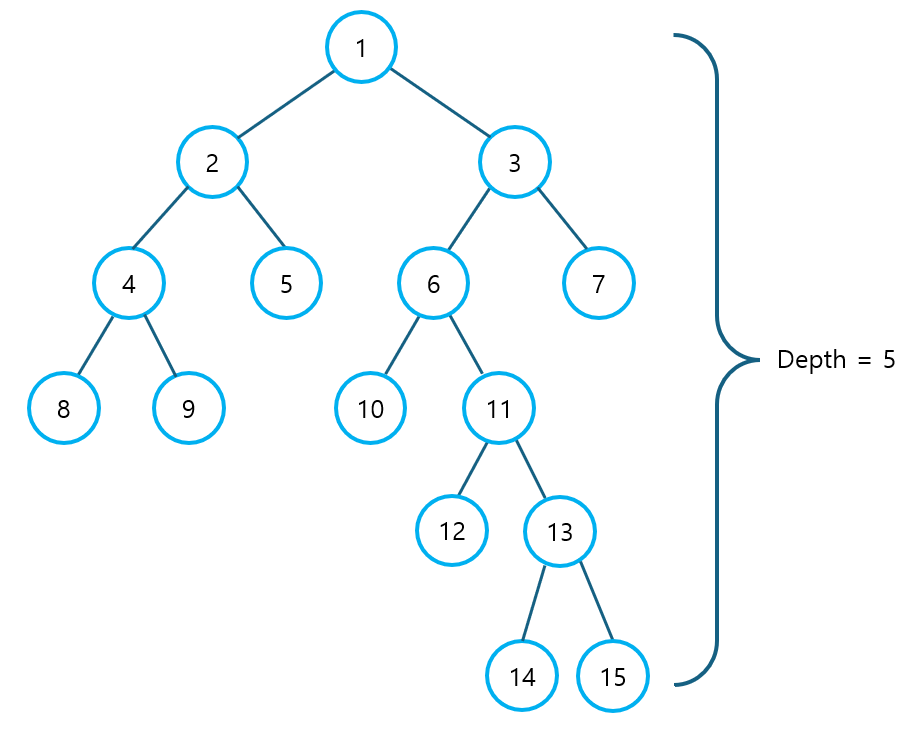
- 아래와 같은 트리에서 트리의 깊이는 5이므로, K = 2가 될 것이다.
2 ^ K이 Depth보다 낮기 때문에, 어떤 노드도2 ^ (K + 1)번째 부모 노드를 가질 수 없다.
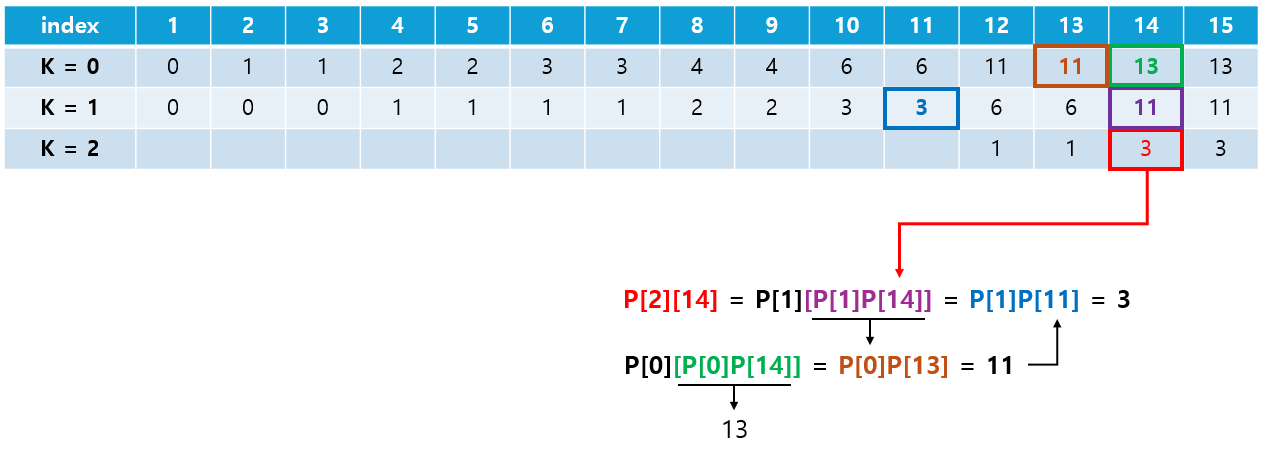
③ K 값과 점화식을 이용해 부모 노드 리스트를 완성한다.
- 먼저 K=0인 경우에 대해 값을 채운다. 이후 K가 1씩 늘어날 때마다, 점화식(K-1번째 값)을 이용하여 나머지 값을 채운다.
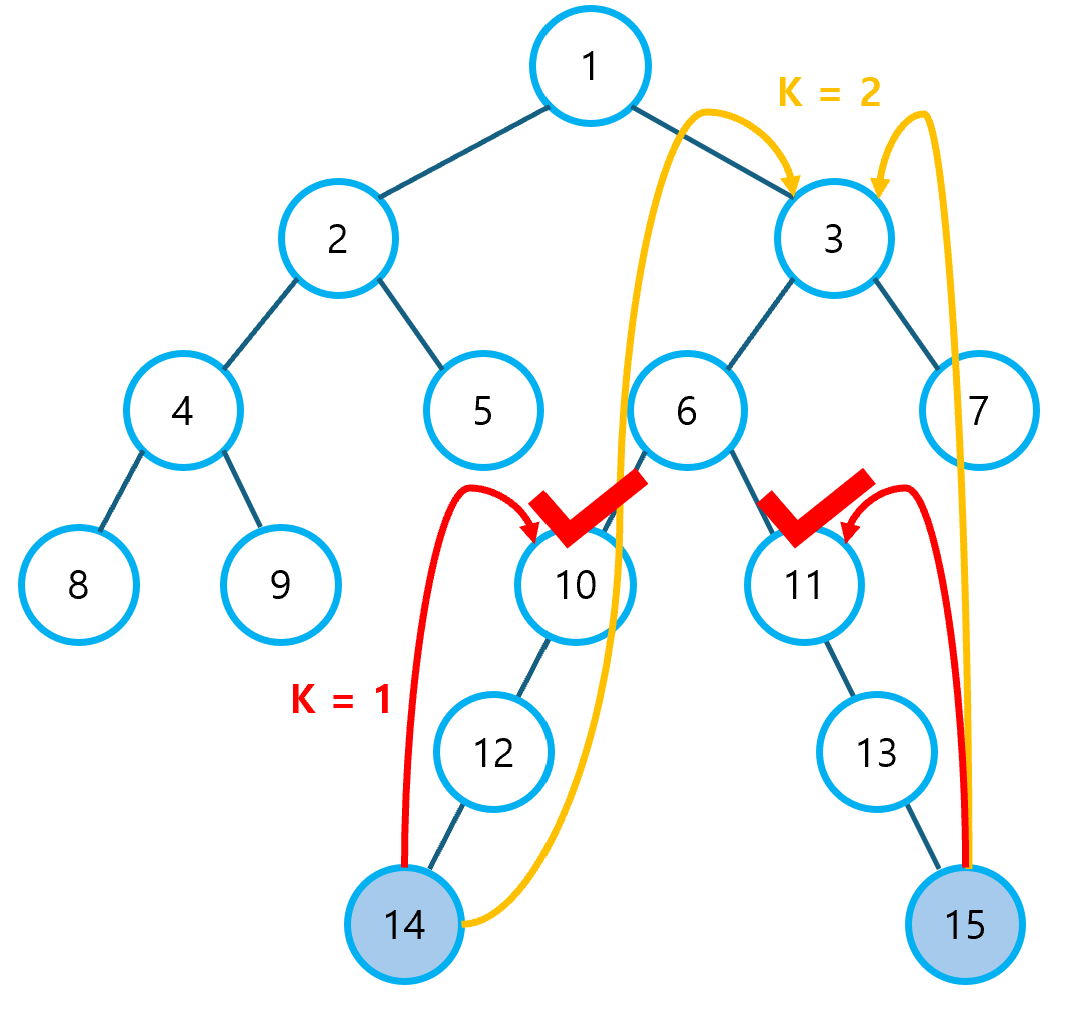
④ depth 배열에 노드의 깊이를 저장한 후, 선택된 두 노드의 깊이 차이를 구한다. 구한 차이 값을 이용해 깊이가 같아질 때까지 2 ^ K번 째 부모 노드로 이동한다.
- K 값은 깊이 차이 D에 대해
2 ^ K < D를 만족하는 K의 최대 값으로 설정한다. - 예를 들어 깊이 차이가 20이면, 처음엔
2 ^ 4만큼 이동한 후,2 ^ 2만큼 이동한다.
⑤ 높이가 맞추어졌다면, K를 최대값에서 1씩 감소시켜 가면서, 최초로 두 부모 노드가 달라지는 K 값을 찾는다. K 값을 찾았다면, K 번째 부모 노드로 이동한다.
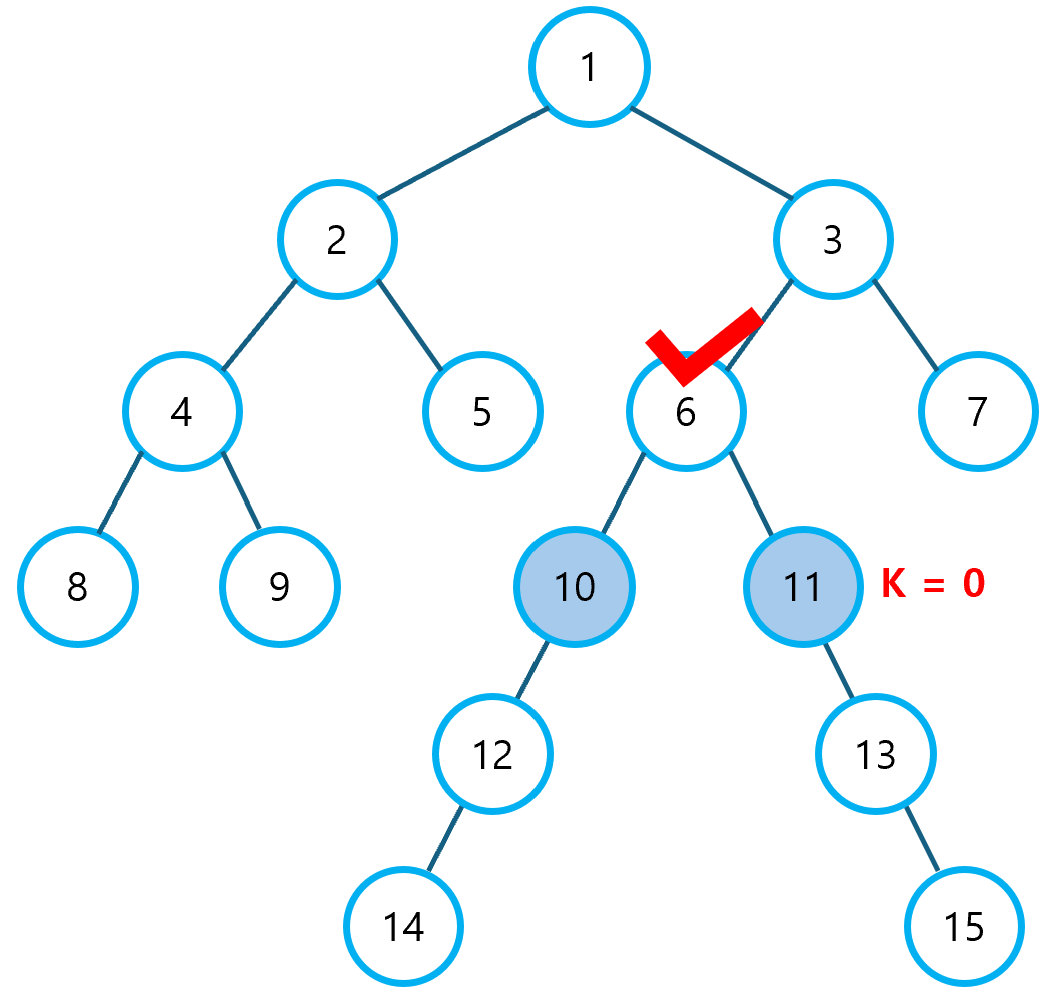
⑥ 계속해서 K 값을 감소시키다가 K가 0이 되면 반복문을 종료한다. 이 때, 두 노드가 동일한 노드라면 해당 노드가 최소 공통 조상이 되고, 다른 노드라면 두 노드의 부모 노드가 최소 공통 조상이 된다.
2. 문제 풀이
1) 일반 LCA 알고리즘을 이용한 풀이
위 문제의 시간 제약은 3초이며, 일반 LCA 알고리즘의 시간 복잡도는 트리의 깊이가 D라고 할 때, O(DM)이 된다. 최악의 경우 D가 50000이 될 수 있기 때문에, 일반 LCA 알고리즘을 이용한 풀이는 시간 초과가 발생할 가능성이 높다.
그래도 일단은 일반 LCA 알고리즘을 구현하는 데에 의의를 두자는 차원에서, 일반 LCA 알고리즘을 적용해 문제를 풀어보도록 하겠다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 8)
N = int(input())
tree = [[] for _ in range(N + 1)]
for i in range(N - 1):
a, b = map(int, input().split())
tree[a].append(b)
tree[b].append(a)
# DFS 탐색을 통해 알아낸 부모 노드와 깊이를 저장하는 배열
depth = [0] * (N + 1)
parent = [0] * (N + 1)
visited = [0] * (N + 1)
def dfs(V, D):
visited[V] = 1
depth[V] = D
# 인접 노드 중 방문하지 않은 노드에 대해 DFS 실행
for i in tree[V]:
if visited[i] == 0:
parent[i] = V
dfs(i, D + 1)
dfs(1, 1) # depth가 1부터 시작한다고 가정
def lca(a, b):
if depth[a] < depth[b]: # 항상 a의 depth가 더 큰 값이 되도록 조작
a, b = b, a
while depth[a] != depth[b]:
a = parent[a] # 선택된 두 노드의 깊이가 다를 경우, 깊이가 같아질 때까지 부모 노드로 이동
# 깊이가 같아진 상태에서는 두 노드 모두 부모 노드로 이동
while a != b:
a = parent[a]
b = parent[b]
return a # 최소 공통 조상 노드 반환
M = int(input())
for i in range(M):
a, b = map(int, input().split())
print(lca(a, b))역시나 예상했던대로 시간 초과가 발생하였다. 최악의 경우 5 * 10 ^ 8번의 연산을 수행하게 되지만, 이 연산이 시간 제약을 크게 상회하는 수치는 아니라는 점에서 PyPy3로 재시도해보았으나, 이번에는 메모리 초과 문제가 발생하였다.
아무래도 일반 LCA로는 풀이하기 어려울 것 같고, 개선된 LCA를 활용하여 풀이하는 편이 좋을 것 같다.
2) 개선된 LCA 알고리즘을 이용한 풀이
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 8)
N = int(input())
tree = [[] for _ in range(N + 1)]
for i in range(N - 1):
a, b = map(int, input().split())
tree[a].append(b)
tree[b].append(a)
# DFS 탐색을 통해 알아낸 부모 노드와 깊이를 저장하는 배열
depth = [0] * (N + 1)
visited = [0] * (N + 1)
# 트리의 깊이 ≥ 2 ^ K를 만족하는 K의 최대 값
MAX_K = 0
while 2 ** MAX_K <= N:
MAX_K += 1
MAX_K -= 1
parent = [[0 for i in range(N + 1)] for j in range(MAX_K + 1)] # K = 0인 경우를 고려해야 하므로, MAX_K + 1개의 행이 필요하다.
def dfs(V, D):
visited[V] = 1
depth[V] = D
# 인접 노드 중 방문하지 않은 노드에 대해 DFS 실행
for i in tree[V]:
if visited[i] == 0:
parent[0][i] = V # K = 0인 경우에 대해 parent 배열을 채운다.
dfs(i, D + 1)
dfs(1, 1) # depth가 1부터 시작한다고 가정
# K를 1씩 늘려가면서 점화식을 이용해 parent 배열의 나머지 부분을 채운다.
for k in range(1, MAX_K + 1):
for n in range(1, N + 1):
parent[k][n] = parent[k - 1][parent[k - 1][n]]
def lca(a, b):
if depth[a] < depth[b]: # 항상 a의 depth가 더 큰 값이 되도록 조작
a, b = b, a
for k in range(MAX_K, -1, -1):
if pow(2, k) <= depth[a] - depth[b]: # K 값은 깊이 차이 D에 대해 2 ^ K < D를 만족하는 K의 최대 값으로 설정한다.
a = parent[k][a] # 구한 차이 값을 이용해 깊이가 같아질 때까지 2 ^ K번 째 부모 노드로 이동한다.
# 깊이가 같아진 상태에서는 두 노드 모두 부모 노드로 이동
for k in range(MAX_K, -1, -1): # K를 최대값에서 1씩 감소시켜 가면서, 최초로 두 부모 노드가 달라지는 K 값을 찾는다
if parent[k][a] != parent[k][b]: # K 값을 찾았다면, K 번째 부모 노드로 이동한다.
a = parent[k][a]
b = parent[k][b]
# K가 0이 되어 반복문이 종료되었을 때,
if a == b: # 1. 두 노드가 동일한 노드라면 해당 노드가 최소 공통 조상이 된다.
return a
else: # 2. 두 노드가 다른 노드라면 두 노드의 부모 노드가 최소 공통 조상이 된다.
return parent[0][a]
M = int(input())
for i in range(M):
a, b = map(int, input().split())
print(lca(a, b))