1. 세그먼트 트리
세그먼트 트리는 대규모 Data Set에서 구간 합, 최대/최소 값을 빠르게 구하기 위해 사용하는 자료구조이다. 세그먼트 트리는 아래의 3단계로 구성된다.
1) 세그먼트 트리 생성하기
① Tree 배열 초기화
- 세그먼트 트리는 Full Binary Tree이므로 배열을 이용한 트리 표현을 사용한다.
- Data Set의 모든 데이터(N 개)가 리프 노드에 할당되어야 한다.
- 이 때, Tree 배열의 크기는
2 ^ k ≥ N을 만족하는 k의 최소 값에 대해2 ^ k * 2를 계산한 수치가 된다.2 ^ k ≥ N: N 개의 모든 데이터를 담기 위해 필요한 리프 노드의 최소 개수2 ^ k * 2: 트리 배열의 사이즈가 리프 노드 개수의 2배가 되는 전 이진 트리의 속성을 이용한 것이다. (배열의 인덱스는 1부터 시작)
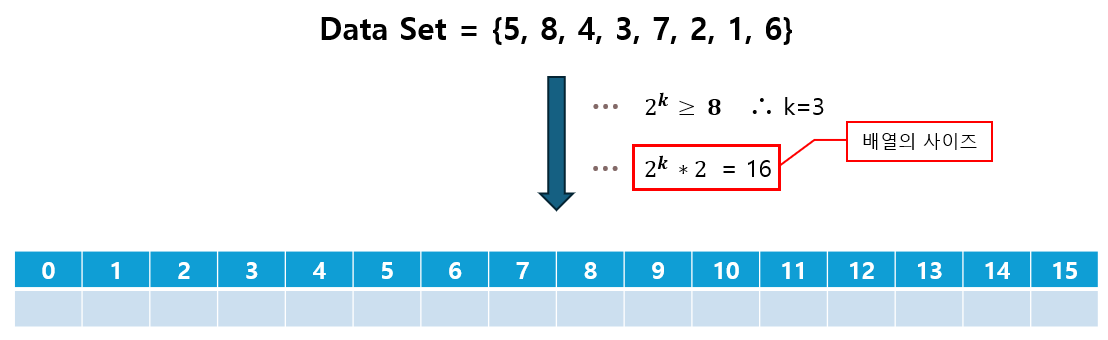
② 리프 노드에 데이터 할당
- 리프 노드의 시작 인덱스는
2 ^ k이므로,2 ^ k번부터 차례대로 데이터를 할당한다.
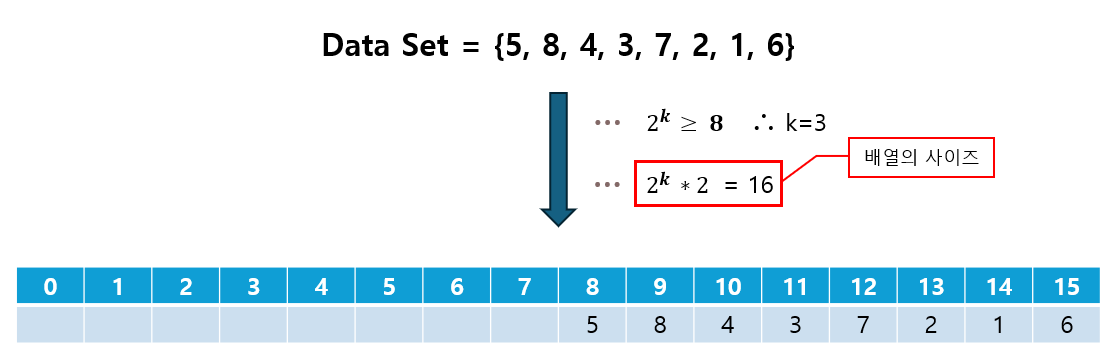
③ 나머지 노드에 값 할당
- 전 이진 트리에서 i 노드의 왼쪽 자식은
2i, 오른쪽 자식은2i + 1인 것을 이용하여 구간 합, 최대 값, 최소 값 중 알아내고자 하는 값을 계산한다. - 참고로, 노드에 값을 할당하는 순서는 높은 인덱스에서 낮은 인덱스 순이다.
- 여기서는 구간 합, 최대 값, 최소 값을 모두 나타내기로 한다.
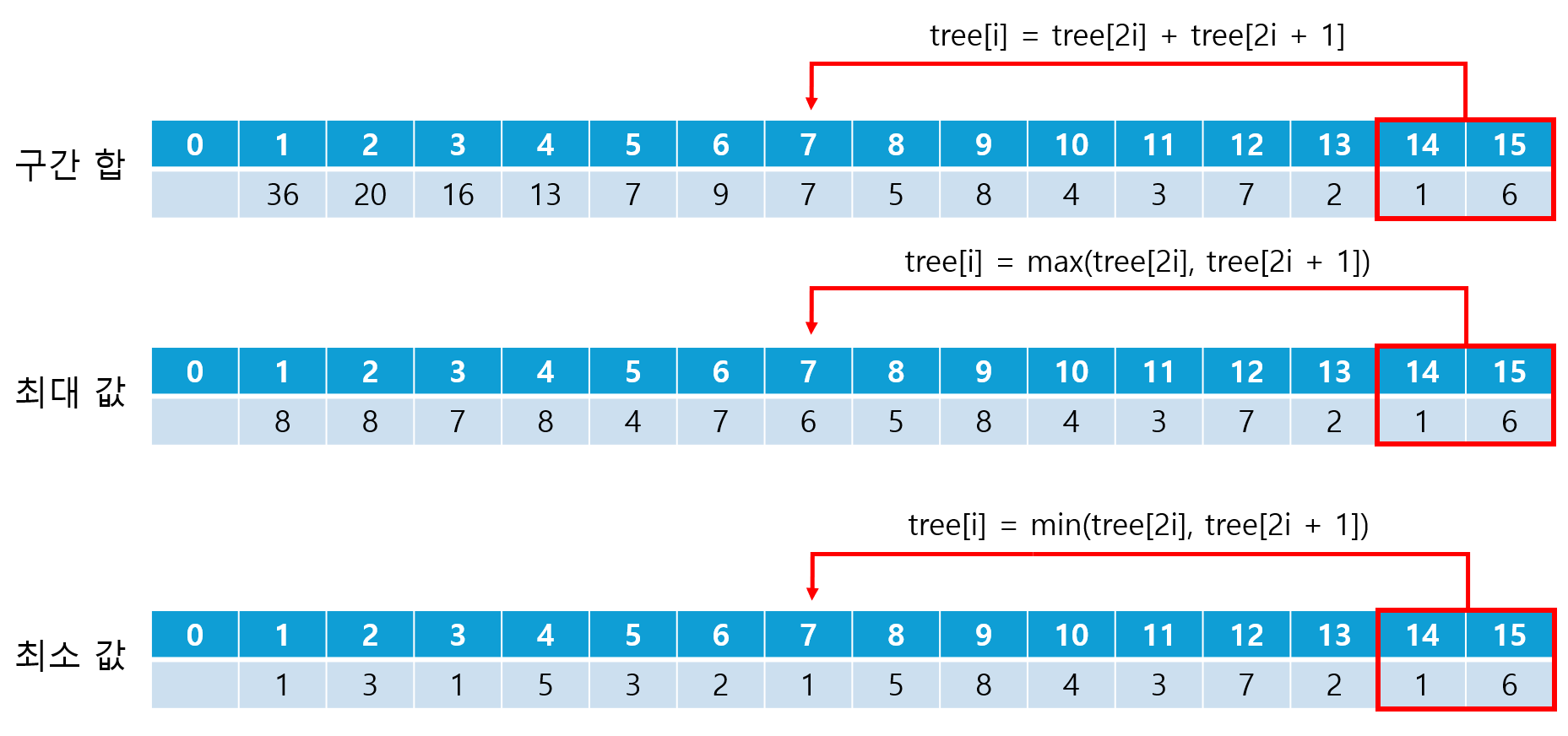
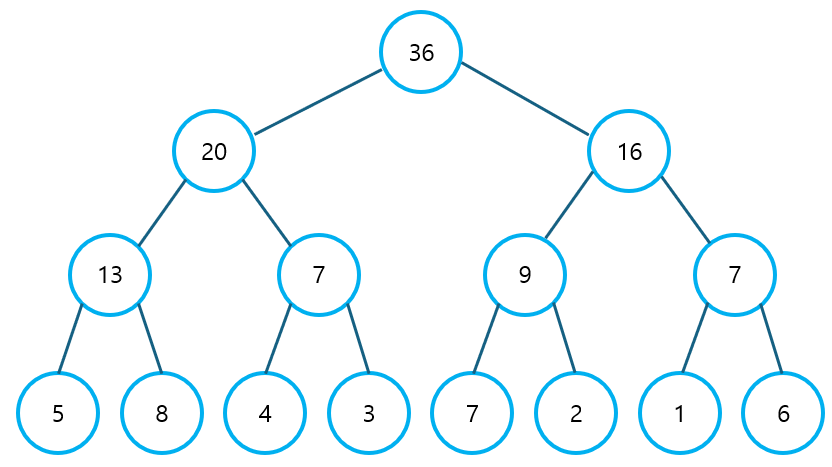
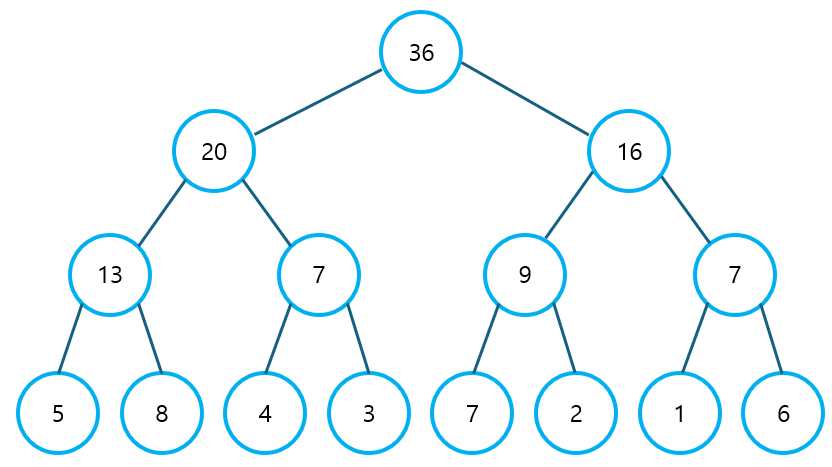
위에 나타난 트리 배열을 트리 형식으로 나타내면 아래와 같다.
2) Range Query 값 구하기
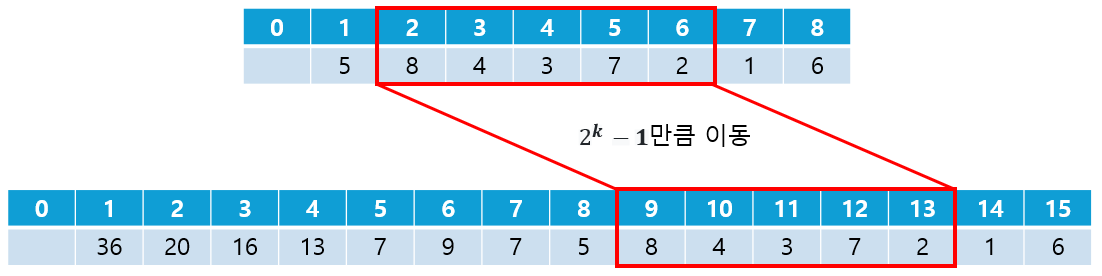
① Query Range를 트리 배열에 알맞게 변경
- 기존 배열의 range를 세그먼트 트리의 range로 변경하려면, 원래의 범위에서
2 ^ k - 1만큼 평행 이동하면 된다.
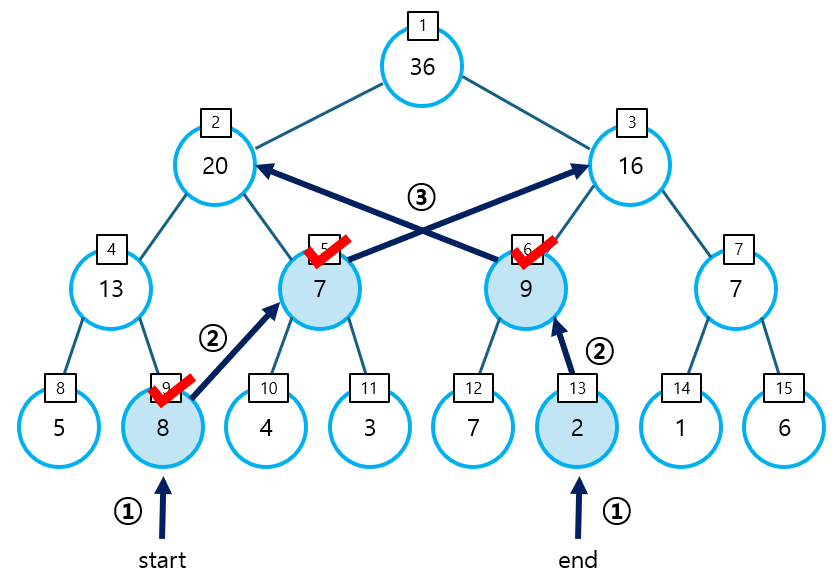
② Query 값 구하기
- 구간 합, 최대/최소 값을 구하는 데에 필요한 노드를 선택하는 과정이다.
- start 인덱스의 값이 홀수이거나, end 인덱스의 값이 짝수이면, 각 노드의 부모는 Query Range를 벗어난다. 따라서, 부모 노드로 이동하지 않고, 해당 노드 자체를 선택한 후, 옆 노드(start 기준 오른쪽, end 기준 왼쪽 노드)의 부모 노드로 이동한다.
- 반대로, start와 end 노드의 부모 노드가 Query Range에 포함되어 있다면, 부모 노드로 이동한다.
- start > end가 될 때까지 아래의 연산을 반복한다.
start = (start + 1) // 2
end = (end - 1) // 2- 선택된 노드를 이용해 원하는 값을 계산한다.
- 구간 합: 선택된 노드들을 모두 더한다.
- 최대 값: 선택된 노드들 중 최대 값을 구한다.
- 최소 값: 선택된 노드들 중 최소 값을 구한다.
3) 데이터 업데이트하기
기존 배열이 변경될 경우, 세그먼트 트리를 그에 맞게 업데이트 해야 할 것이다. 세그먼트 트리의 데이터를 업데이트 하는 방법을, 구간 합 트리와 최대/최소 값 트리에서 각각 알아보자.
① 구간 합
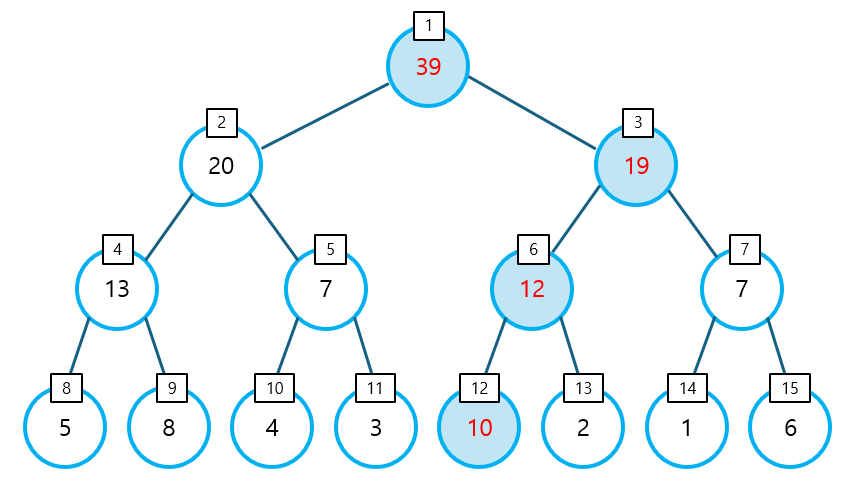
- 모든 부모(조상) 노드의 값에, 새로운 데이터와 기존 데이터 사이의 차이만큼을 더한다.
- 아래의 그림은 12번 인덱스의 값이 7에서 10으로 변경됨에 따라 모든 부모(조상) 노드의 값이 3씩 더해진 모습을 나타낸 것이다.
② 최대/최소 값
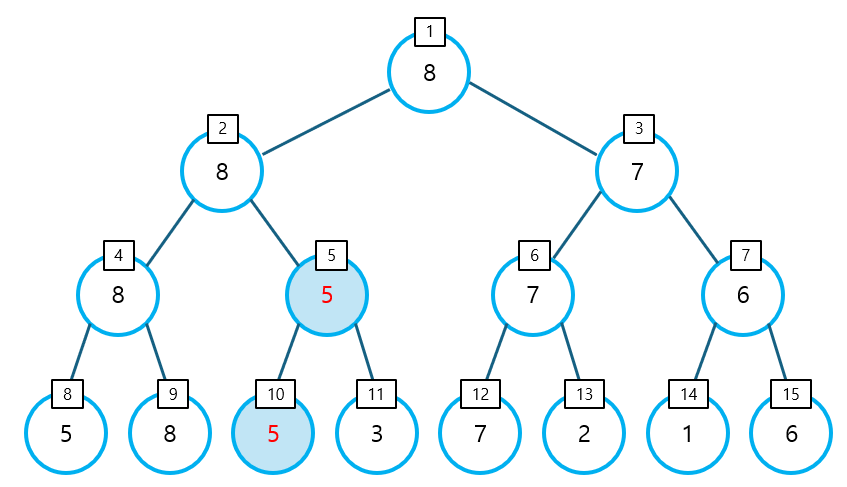
- 변경된 노드를 기점으로 최대/최소를 다시 계산한다.
- 최대/최소 값이 갱신되지 않았다면, 업데이트를 종료한다.
- 아래의 그림은 10번 인덱스의 값이 4에서 5로 변경됨에 따라, 최대 값을 다시 계산하는 모습을 나타낸 것이다.
일반 구간 합 배열과 달리, 세그먼트 트리는 데이터의 업데이트를 효율적으로 처리할 수 있다. 따라서 데이터의 변경이 없는 상황에서 구간 합을 구하는 문제는 구간 합 배열로 풀이하고, 데이터의 변경이 잦은 상황에서 구간 합을 구하는 문제는 세그먼트 트리로 풀이해야 한다. (구간 합 배열에 대해서는 아래의 포스팅을 참조하라.
>> 구간 합 배열
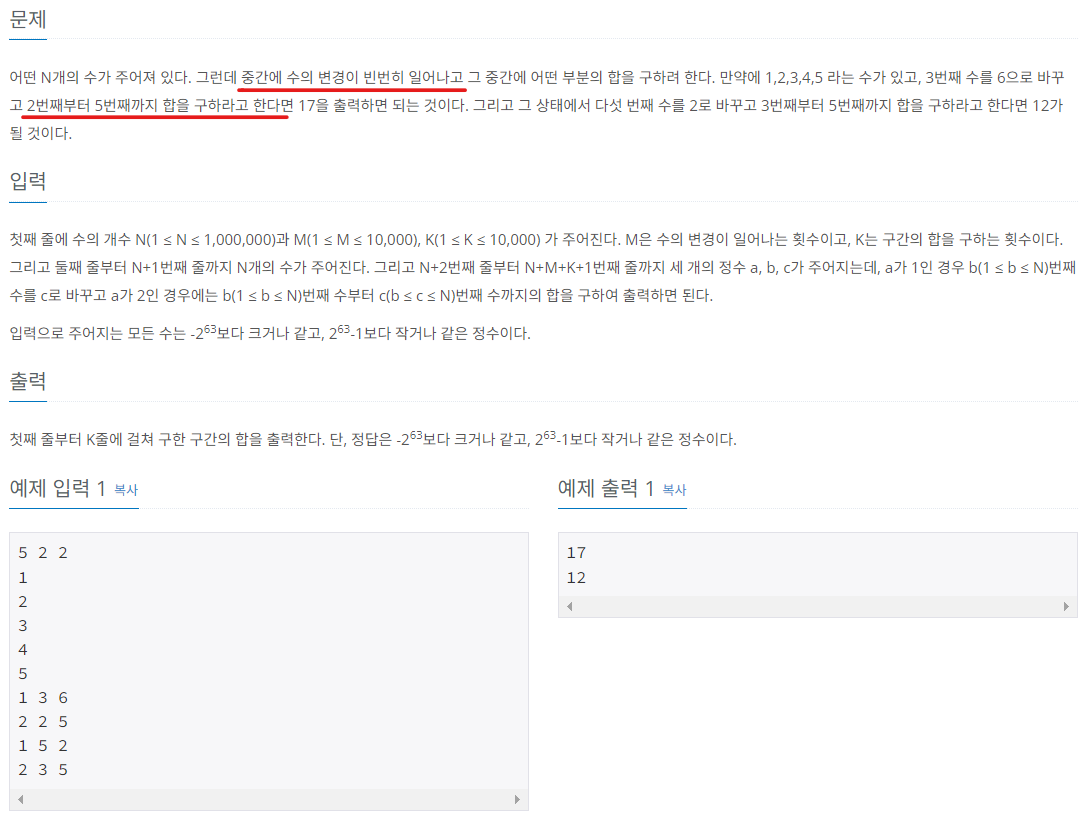
2. 문제 풀이
1) 구간 합 구하기
데이터의 변경이 잦은 상황에서 구간 합을 구하는 문제이므로, 전형적인 세그먼트 트리 문제이다. (만약 이 문제를 기존 배열에서 직접 구간 합을 구하는 방식으로 구현하거나, 구간 합 배열로 구현할 경우 시간 초과가 발생할 것이다.) 지금까지 배운 내용을 바탕으로 위 문제를 풀어보자.
import sys
input = sys.stdin.readline
N, M, K = map(int, input().split())
length = N
height = 0 # k 값
while length > 0: # 2 ^ k ≥ N을 만족하는 k의 최소 값을 구하는 과정
length //= 2
height += 1
treeSize = 2 ** (height + 1) # 트리 배열의 사이즈(= 2 ^ k * 2)
leafStartIdx = 2 ** height # 리프 노드의 시작 인덱스
tree = [0] * (treeSize)
# 데이터를 리프 노드에 저장
for i in range(leafStartIdx, leafStartIdx + N): # 기존 배열의 원소 수가 리프 노드 수보다 작거나 같으므로, treeSize를 끝 범위로 설정하면 안됨.
tree[i] = int(input())
# 나머지 노드에 값 할당
def setTree(i):
while i > 1: # 루트 노드까지만 구하면 됨.
tree[i // 2] += tree[i] # 자식 노드의 인덱스가 2i, 2i + 1인 것을 이용하여 구간 합 계산
i -= 1
# 데이터 업데이트 함수
def updateValue(index, value):
diff = value - tree[index] # 기존 데이터와 새로운 데이터 간의 차이
while index > 0: # 루트 노드에 이르기까지 모든 부모(조상) 노드의 값에 diff만큼을 더함
tree[index] = tree[index] + diff
index //= 2
# 구간 합 계산 함수
def getIntervalSum(start, end):
intervalSum = 0
while start <= end:
if start % 2 == 1: # start의 인덱스가 홀수이면, 해당 노드의 값을 intervalSum에 포함
intervalSum += tree[start]
if end % 2 == 0: # end의 인덱스가 짝수이면, 해당 노드의 값을 intervalSum에 포함
intervalSum += tree[end]
# 부모 노드로 이동
start = (start + 1) // 2
end = (end - 1) // 2
return intervalSum
setTree(treeSize - 1) # 높은 인덱스에서 낮은 인덱스 순서로 노드에 값을 할당
for i in range(M + K):
query, start, end = map(int, input().split())
if query == 1:
updateValue(start + leafStartIdx -1, end) # 기존 배열의 range를 세그먼트 트리의 range로 변경하하기 위해 2 ^ k - 1만큼 평행 이동
elif query == 2:
start += leafStartIdx -1
end += leafStartIdx -1
print(getIntervalSum(start, end))트리 자료구조는 인덱스를 계산하는 부분에서 실수하기 쉽기 때문에, 이 부분을 주의 깊게 연습해보기 바란다.
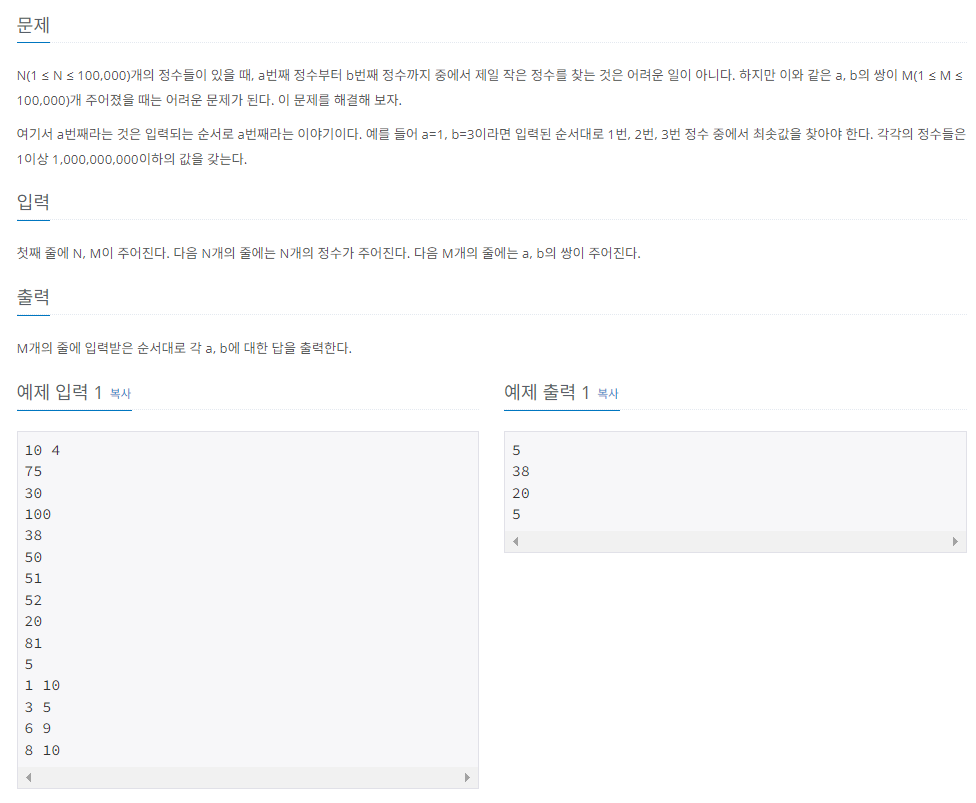
2) 최소 값 찾기
구간에서의 최소 값을 구하는 문제 역시 세그먼트 트리를 활용해 풀이해야 하는 문제이다. (그래도 먼저는 일반 배열을 이용해 최소 값을 구할 때의 시간 복잡도를 계산해보기 바란다. 이 문제에서는 시간 초과가 날 것이 분명하므로, 바로 세그먼트 트리를 사용하기로 한다.)
다만, 데이터 업데이트가 발생하지 않기 때문에 직전 문제에서 구현하였던 updateValue 메서드는 생략할 수 있다.
import sys
input = sys.stdin.readline
N, M = map(int, input().split())
length = N
height = 0 # k 값
while length > 0: # 2 ^ k ≥ N을 만족하는 k의 최소 값을 구하는 과정
length //= 2
height += 1
treeSize = 2 ** (height + 1) # 트리 배열의 사이즈(= 2 ^ k * 2)
leafStartIdx = 2 ** height # 리프 노드의 시작 인덱스
tree = [sys.maxsize] * (treeSize) # 구간 합을 구할 때와 달리 최소 값을 구할 때는, 매우 큰 값으로 초기화해야 함.
# 데이터를 리프 노드에 저장
for i in range(leafStartIdx, leafStartIdx + N): # 기존 배열의 원소 수가 리프 노드 수보다 작거나 같으므로, treeSize를 끝 범위로 설정하면 안됨.
tree[i] = int(input())
# 나머지 노드에 값 할당
def setTree(i):
while i > 1: # 루트 노드까지만 구하면 됨.
tree[i // 2] = min(tree[i // 2], tree[i]) # 자식 노드의 인덱스가 2i, 2i + 1인 것을 이용하여 구간 합 계산
i -= 1
# 최소 값 계산 함수
def getMin(start, end):
Min = sys.maxsize # 구간 합을 구할 때와 달리, 매우 큰 값으로 초기화
while start <= end:
if start % 2 == 1: # start의 인덱스가 홀수이면, 해당 노드의 값이 최소 값인지 검사
Min = min(Min, tree[start])
if end % 2 == 0: # end의 인덱스가 짝수이면, 해당 노드의 값이 최소 값인지 검사
Min = min(Min, tree[end])
# 부모 노드로 이동
start = (start + 1) // 2
end = (end - 1) // 2
return Min
setTree(treeSize - 1) # 높은 인덱스에서 낮은 인덱스 순서로 노드에 값을 할당
for i in range(M):
start, end = map(int, input().split())
start += leafStartIdx -1
end += leafStartIdx -1
print(getMin(start, end))구간 합을 구할 때와 최소 값을 구할 때, 어떤 부분이 달라지는지를 유심히 살펴보기 바란다.
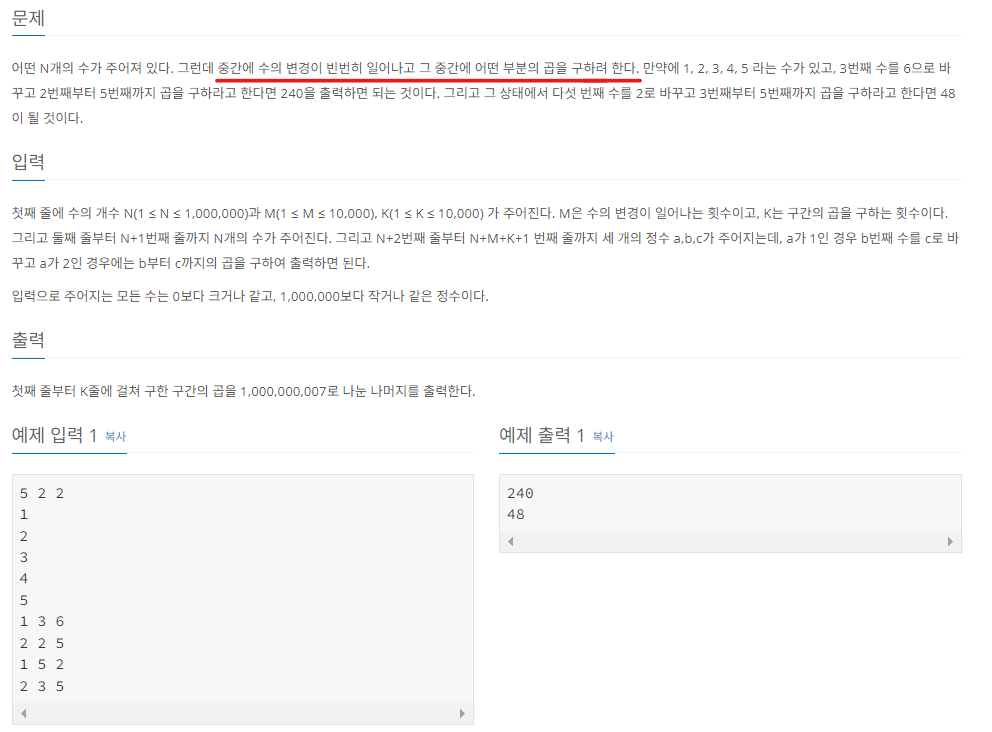
3) 구간 곱 구하기
구간 합이 아닌 구간 곱이라는 점만 빼면, 1번 문제와 유사해보이기에 세그먼트 트리를 이용하여 풀이하기로한다. 다만, 한 가지 주의해야 할 것은 구간 합 세그먼트 트리에서 데이터를 업데이트 할 때에는 변경된 자식의 옆 자식은 고려하지 않아도 되었지만, 구간 곱 세그먼트 트리에서는 변경된 자식의 옆 자식까지 고려하여 부모 노드의 값을 다시 계산해야 한다는 것이다.
예를 들어, 왼쪽 자식이 2, 오른쪽 자식이 3, 부모 노드가 6이었다고 하자. 이 때, 왼쪽 자식이 4로 변경된다면, 6 // 2 * 4로 부모 노드를 업데이트 하면 되었을 것이다. 만약 이 로직의 문제가 없다면, 오른쪽 자식은 전혀 고려하지 않아도 되었을 것이다.
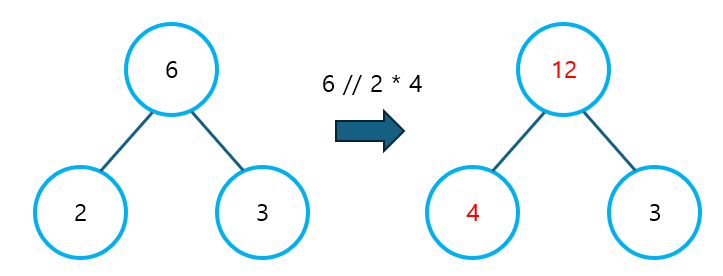
그러나 위 로직은 부모 노드의 값이 0인 경우에 대해, 제대로 동작하지 않는다. 0을 0으로 나눌 때, ZeroDivisionError가 발생하면서, 프로그램이 종료되어 버릴 것이다.
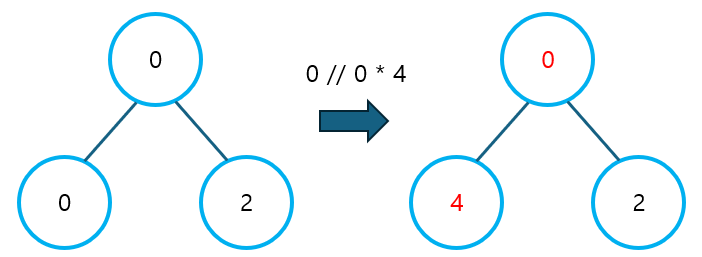
따라서, 변경된 노드와 그 옆 노드의 값을 곱하여 새롭게 계산된 값으로, 부모 노드의 값을 업데이트해야 한다.
import sys
input = sys.stdin.readline
N, M, K = map(int, input().split())
length = N
height = 0 # k 값
MOD = 1000000007
while length > 0: # 2 ^ k ≥ N을 만족하는 k의 최소 값을 구하는 과정
length //= 2
height += 1
treeSize = 2 ** (height + 1) # 트리 배열의 사이즈(= 2 ^ k * 2)
leafStartIdx = 2 ** height # 리프 노드의 시작 인덱스
tree = [1] * (treeSize) # 구간 곱을 구할 때에는 1로 초기화해야 함.
# 데이터를 리프 노드에 저장
for i in range(leafStartIdx, leafStartIdx + N): # 기존 배열의 원소 수가 리프 노드 수보다 작거나 같으므로, treeSize를 끝 범위로 설정하면 안됨.
tree[i] = int(input())
# 나머지 노드에 값 할당
def setTree(i):
while i > 1: # 루트 노드까지만 구하면 됨.
tree[i // 2] = (tree[i // 2] * tree[i]) % MOD # 자식 노드의 인덱스가 2i, 2i + 1인 것을 이용하여 구간 합 계산
i -= 1
# 데이터 업데이트 함수
def updateValue(index, value):
tree[index] = value
index //= 2
while index > 0: # 루트 노드에 이르기까지 모든 부모(조상) 노드의 값을 새로 구함(변경된 노드의 옆 노드까지 고려)
tree[index] = (tree[index * 2] * tree[index * 2 + 1]) % MOD
index //= 2
def getIntervalMul(start, end):
intervalMul = 1
while start <= end:
if start % 2 == 1: # start의 인덱스가 홀수이면, 해당 노드의 값을 intervalMul에 포함
intervalMul = (intervalMul * tree[start]) % MOD
if end % 2 == 0: # end의 인덱스가 짝수이면, 해당 노드의 값을 intervalMul에 포함
intervalMul = (intervalMul * tree[end]) % MOD
# 부모 노드로 이동
start = (start + 1) // 2
end = (end - 1) // 2
return intervalMul
setTree(treeSize - 1) # 높은 인덱스에서 낮은 인덱스 순서로 노드에 값을 할당
for i in range(M + K):
query, start, end = map(int, input().split())
if query == 1:
updateValue(start + leafStartIdx -1, end) # 기존 배열의 range를 세그먼트 트리의 range로 변경하하기 위해 2 ^ k - 1만큼 평행 이동
elif query == 2:
start += leafStartIdx -1
end += leafStartIdx -1
print(getIntervalMul(start, end))중요한 내용은 아니지만 참고할만한 내용으로, 문제에서 "1,000,000,007로 나눈 나머지를 출력하라"라는 말의 의미에 대해서 간단히 알아보기로 하자. 위 문제와 같이 매우 큰 수에 대한 곱셈을 계산하는 문제는 정수 Overflow가 발생하기 쉽다. 물론, 파이썬에서는 매우 큰 숫자도 모두 허용하기 때문에 큰 문제가 안 되지만, 코딩 테스트 문제는 파이썬이 아닌 다른 언어로도 풀이할 수 있어야 하기 때문에, 주로 구해진 값의 나머지를 출력하도록 문제를 출제한다.
그러면 어떤 수에 대해 나눈 나머지를 출력해야 할까? 주로 사용되는 숫자는 1000000007(10억 7) 또는 1000000009(10억 9)이다. 이 숫자를 사용하는 이유는 int 값의 범위와 관련이 깊다. C/C++ 기준 int의 범위는 -2147483648 ~ 2147483647로 약 -20억부터 +20억까지이다. 즉, int 범위의 절반 정도의 연산만 허용하겠다는 의미인 것이다. (10억과 가장 가까운 두 소수를 선택한 것이다.)
int 범위의 절반만 사용하는 이유는 int 범위에 근접한 값을 사용할 경우, 허용된 값끼리의 덧셈만으로도 Overflow가 발생할 수 있으며, int 범위에 비해 턱 없이 작은 값을 사용하면 효율성이 떨어지기 때문에, 적절하게 int 범위의 절반 정도만 사용하기로 한 것이다.
하지만, 여전히 허용된 범위 내에서의 곱셈에서 정수 Overflow가 발생할 가능성이 존재한다. 이 문제를 해결하기 위해 아래와 같은 연산자 분배법칙을 사용할 수 있다.
(A + B) % M = ((A % M) + (B % M)) % M
(A - B) % M = ((A % M) - (B % M)) % M
(A * B) % M = ((A % M) * (B % M)) % M(A * B) % M = ((A % M) * (B % M)) % M는 A * B에서 Overflow가 나는 것을 방지하는 유용한 항등식이다. 다만, 파이썬에서는 정수 Overflow가 거의 발생하지 않기 때문에 직접적으로 사용할 일은 없을 것이다. 사실 출력되는 결과에만 Modulus 연산을 적용해도, 문제 풀이에 전혀 지장이 없는 경우가 대부분이다.
그러나 곱셈 결과에 대한 Modulus를 출력하는 문제에서는, 자칫 곱셈의 값이 너무 방대해져 시간 초과가 발생할 수 있다. 위의 구간 곱 구하기 문제가 바로 이러한 문제이다. 구간 곱의 결과를 Modulus 없이 세그먼트 트리에 저장하다보면, 곱셈의 결과가 매우 방대해지면서 결국 시간 초과가 발생한다. 따라서, 이러한 경우에는 곱셈 결과에 바로 Modulus를 적용하여 풀이해야 한다.