파이썬에서는 이미 sort() 함수를 제공하고 있기 때문에, 사실 정렬을 직접 구현해야 하는 일은 많지 않습니다. 오히려 코딩 테스트에서는 정렬을 구현하는 방법보다도 정렬 알고리즘이 어떤 방식으로 정렬을 수행하는지를 이해하는 것이 더 중요할 수 있습니다. 따라서, 문제 풀이보다는 정렬 알고리즘의 핵심 개념과 구현 방법에 초점을 맞추어 설명하도록 하겠습니다.
특히, 이번 포스팅에서는 이중 for문을 이용해 정렬을 수행하는 O(N^2) 정렬 알고리즘에 대해 알아보기로 하겠습니다.
1. Bubble Sort
1) 개념
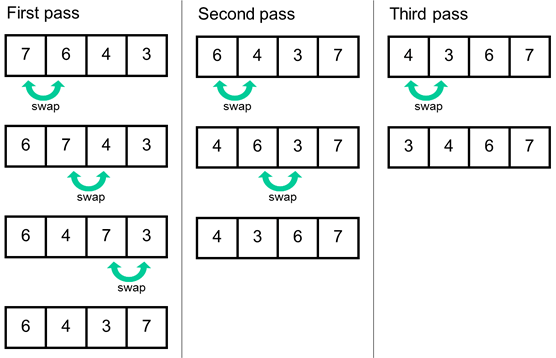
버블 정렬은 가장 큰 값을 맨 뒤로 보내는 과정을 반복하며 정렬을 수행한다. 버블 정렬 구현에 사용되는 변수는 아래와 같다. (배열의 Size를 N, 이중 for문의 외부 루프와 내부 루프에 사용되는 변수를 각각 i, j라고 하자.)
① i
- i는 N-1번 반복된다. 이는 제일 큰 원소를 뒤로 보내는 과정을 N-1번 수행한다는 의미이다.
- N번 수행하지 않는 이유는 N-1번 수행하는 것만으로 가장 작은 원소가 이미 맨 앞에 배치되기 때문이다. (물론, N번 반복해도 정상적으로 동작한다.)
② j
- j는 N-i-1번 반복된다. j는 각 루프당 필요한 대소 비교의 횟수를 의미한다.
- 가장 큰 원소를 맨 뒤로 보내기 위해서는 N-1번의 대소 비교가 필요하며, 정렬이 완료된 원소를 제외하기 위해 i를 빼는 것이다.
2) 구현
arr = [3, 2, 4, 5, 1]
N = len(arr)
for i in range(N-1):
for j in range(N-i-1):
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]위 코드에서 부등호 방향만 변경하면, 내림차순으로 정렬하는 것도 가능하다.
3) 문제 풀이
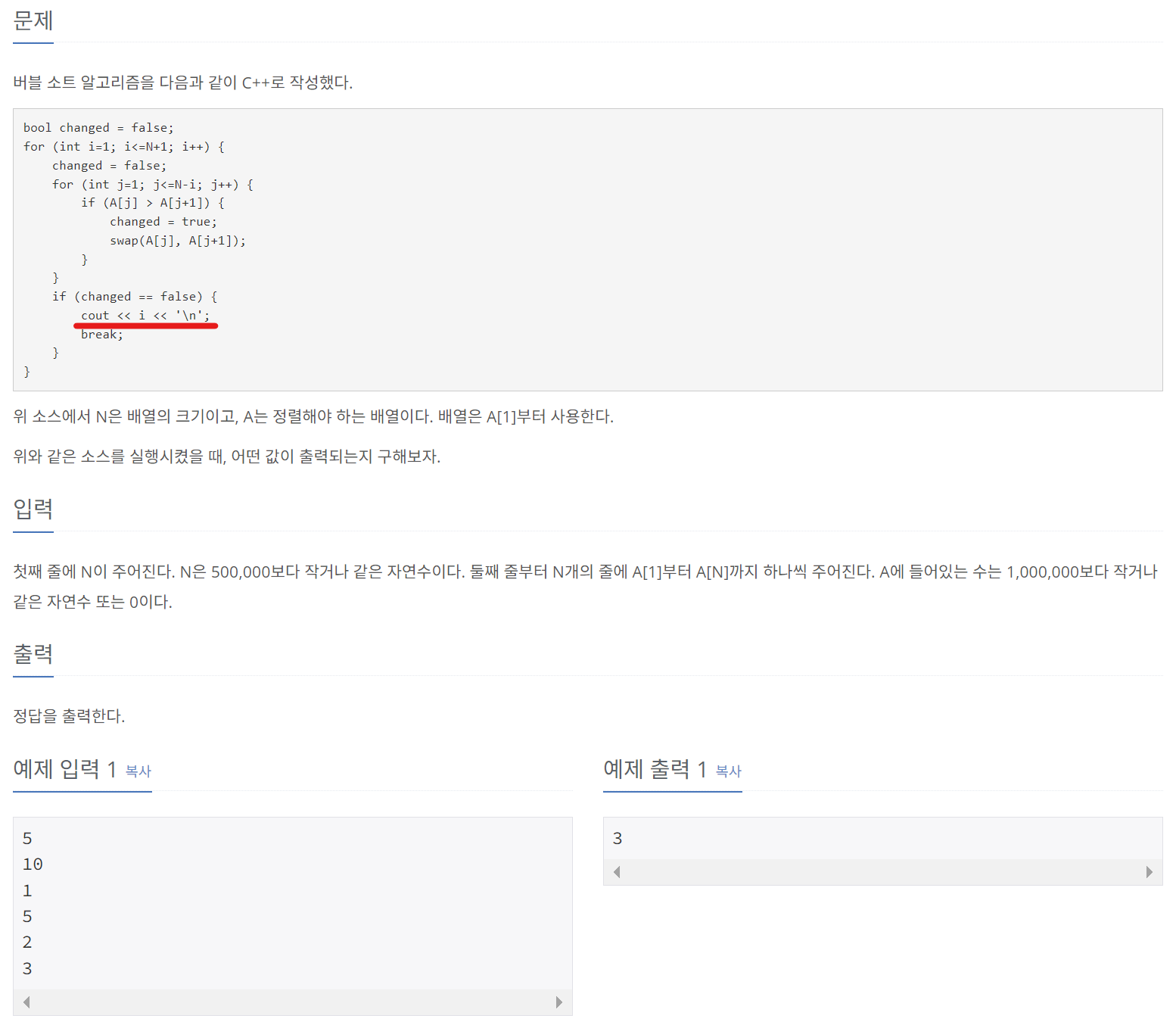
위 문제는 버블 정렬에서 Swap이 한번도 일어나지 않은 루프가 언제인지를 알아내는 문제이다. 당연히 위 코드를 적절히 파이썬 코드로 변경만 해주면, 쉽게 해결될 문제이기에 문제에서 시간 제약을 걸어두었다.
시간 제약은 2초인데 N의 범위는 500,000이므로, O(N^2)인 버블 정렬을 그대로 이용할 경우, 시간 초과가 발생할 것이다. 그러므로, Swap이 한번도 일어나지 않은 루프를 찾기 위한, 다른 방법을 모색해 보아야 할 것이다.
사실 버블 정렬의 내부 루프(2차 루프)에서 Swap이 한번도 일어나지 않았다는 것은, 이미 정렬이 완료된 상태임을 의미한다. 따라서, 위 문제의 출력 결과는 곧 버블 정렬이 몇번째 루프에서 완료되는지에 1을 더한 수치가 될 것이다. 여기서 1을 더하는 이유는, 정렬이 완료된 이후에 Swap이 한번도 일어나지 않았다는 것을 확인하기 위해 한번의 루프를 추가로 수행해야 하기 때문이다.
그렇다면 버블 정렬이 완료되기 위해 필요한 루프의 횟수는 어떻게 구할 수 있을까? 버블 정렬에는 한 가지 특징이 있는데, 이는 한 루프에서 각 원소가 왼쪽(앞쪽)으로 이동하는 경우는 최대 한번밖에 발생하지 않는다는 것이다. 즉, 한 원소가 한 루프 내에서 2번 이상 왼쪽으로 이동하는 일은 발생하지 않는다.
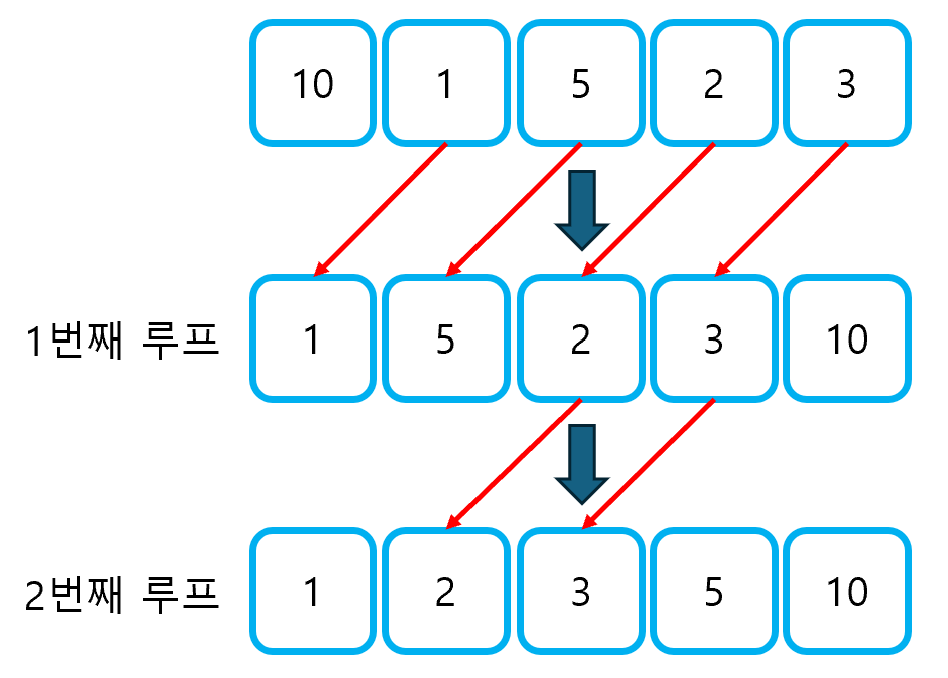
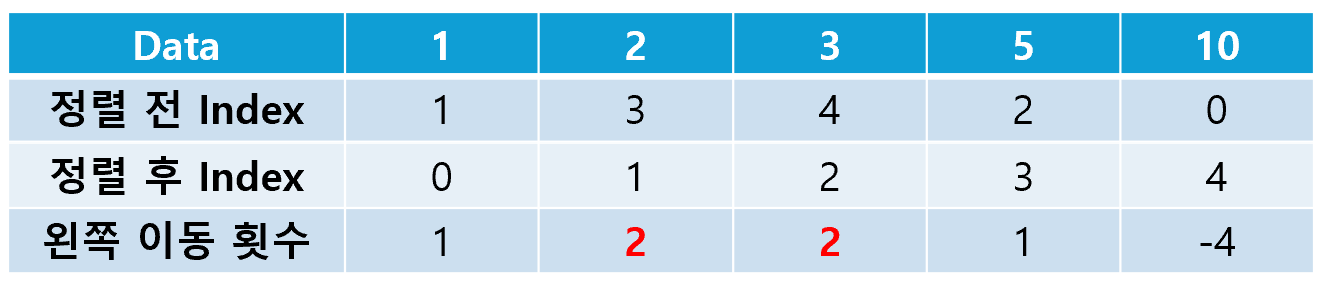
버블 정렬이 완료되려면, 더 이상 왼쪽으로 이동하는 원소가 없어야 한다. 그러므로, 각 원소가 왼쪽으로(앞으로) 이동한 횟수의 최대 값과, 정렬이 완료되기 위해 필요한 루프의 횟수가 같다. 위 그림에서도, 왼쪽으로 이동하는 횟수의 최대 값이 2이므로, 두번째 루프에서 정렬이 완료되는 것을 확인할 수 있다.
왼쪽으로 이동한 횟수는 정렬 전 Index에서 정렬 후 Index를 빼는 것으로 구할 수 있다. 이렇게 해서 구해진 값 중 최대 값을 찾고, 그 값에 1을 더하면 문제 풀이가 완료될 것이다.
import sys
input = sys.stdin.readline
N = int(input())
lst = []
for i in range(N):
lst.append([int(input()), i]) # 원소와 정렬 전 index를 모두 저장
lst.sort() # 배열의 첫번째 요소를 기준으로 정렬
Max = 0
for i in range(N): # i는 정렬 후 index에 해당
Max = max(Max, lst[i][1] - i) # 정렬 전 index - 정렬 후 index의 최대 값
print(Max + 1)2. Selection Sort
1) 개념
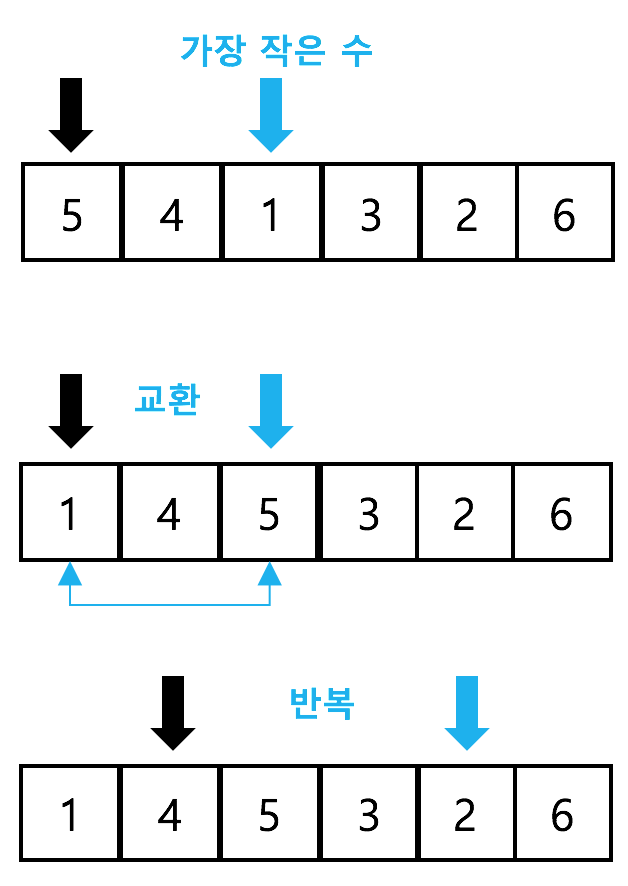
선택 정렬은 최소 값이 위치한 인덱스를 탐색한 후, 해당 인덱스의 원소와 맨 앞의 원소를 swap하는 방식으로 정렬을 수행한다. 선택 정렬 구현에 사용되는 변수는 아래와 같다.
① i
- i는 탐색한 최소 값을 배치할 인덱스를 나타낸다.
- 마지막 인덱스에 대해서는 정렬을 수행하지 않아도 되기 때문(이미 최소 값들이 앞에 배치되었기 때문)에 i는 N-1번만 반복하면 된다.
② j
- j는 i 이후에 위치한 원소들을 순회하기 위해 사용된다.
- 즉, 각 루프마다 i+1번 인덱스부터 끝까지를 순회한다.
③ min_idx
- 최소 값이 위치한 인덱스를 찾아내기 위해 min_idx 변수를 사용한다.
- 초기 값은 i로 설정되며, 대소 비교를 통해 지속적으로 업데이트된다.
2) 구현
arr = [3, 2, 4, 5, 1]
N = len(arr)
for i in range(N-1):
min_idx = i
for j in range(i+1, N):
if arr[min_idx] > arr[j]:
min_idx = j
arr[min_idx], arr[i] = arr[i], arr[min_idx]위 코드에서 min_idx를 max_idx로 변경하고 부등호 방향만 바꿔주면, 내림차순 정렬을 수행할 수 있다.
3. Insertion Sort
1) 개념
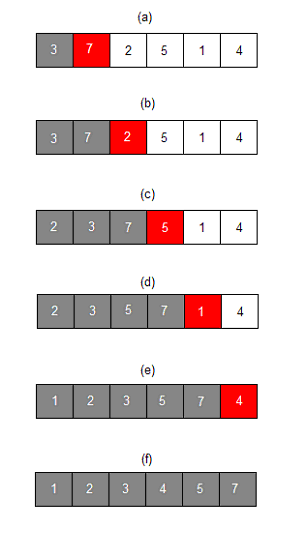
삽입 정렬은 먼저 배열을 정렬부와 비정렬부로 구분한다. 이 때, 0번 인덱스의 원소는 이미 정렬되어 있다고 가정한다. 비정렬부에 존재하는 원소를 순차적으로 정렬부로 삽입하며, 정렬이 유지될 수 있도록 적절한 위치에 배치하는 과정을 통해 정렬을 수행한다.
① i
- i는 비정렬부에서 정렬부로 넘어오는 원소의 인덱스를 의미한다. 즉, 1번 인덱스부터 끝까지 반복된다.
- i가 1부터 시작하는 이유는 0번 인덱스의 원소는 이미 정렬되어 있다고 가정하기 때문이다.
② j
- j는 i번부터 1번 인덱스까지 역순으로 정렬부를 순회한다.
- j를 역순으로 반복하는 이유는 비정렬부에서 정렬부로 넘어오는 원소의 인덱스인 i부터 왼쪽으로 이동하면서 대소 비교를 진행하기 위함이다.
- arr[j-1] < arr[j]를 만족한다면, 이는 정렬이 완료되었음을 의미하므로, 현재 루프를 탈출한다.
2) 구현
arr = [3, 2, 4, 5, 1]
N = len(arr)
for i in range(1, N):
for j in range(i, 0, -1):
if arr[j-1] > arr[j]:
arr[j-1], arr[j] = arr[j], arr[j-1]
else:
break마찬가지로 부등호 방향만 바꾸면, 내림차순으로 정렬할 수 있다.
4. 버블 정렬 VS 선택 정렬 VS 삽입 정렬
각 정렬이 어떤 방식으로 정렬을 수행하는지 헷갈릴 때가 많다. 그러므로, 3가지 정렬 방식에 대해서 확실히 구분하는 방법에 대해 알아보자.
① Bubble Sort
- 연쇄적인 Swap이 일어나는 모습이 마치 "거품"처럼 보인다는 뜻에서 붙여진 이름이다.
- 가장 큰 원소를 차례로 뒤로 보내므로, 뒤에서부터 정렬이 진행된다.
② Selection Sort
- 현재 인덱스에 배치해야 하는 원소를 "선택"하는 방식의 정렬 알고리즘이다.
- 작은 값을 차례로 앞으로 보내므로, 앞에서부터 정렬이 진행된다.
③ Insertion Sort
- 비정렬부에서 정렬부로 "삽입"하는 방식의 정렬 알고리즘이다.
- Selection Sort와 마찬가지로 배열의 앞에서 정렬이 수행되지만, 맨 앞의 원소와 배열 전체의 최소값이 다를 수 있다는 점에서 차이가 있다.