자료구조 기본 - Tree

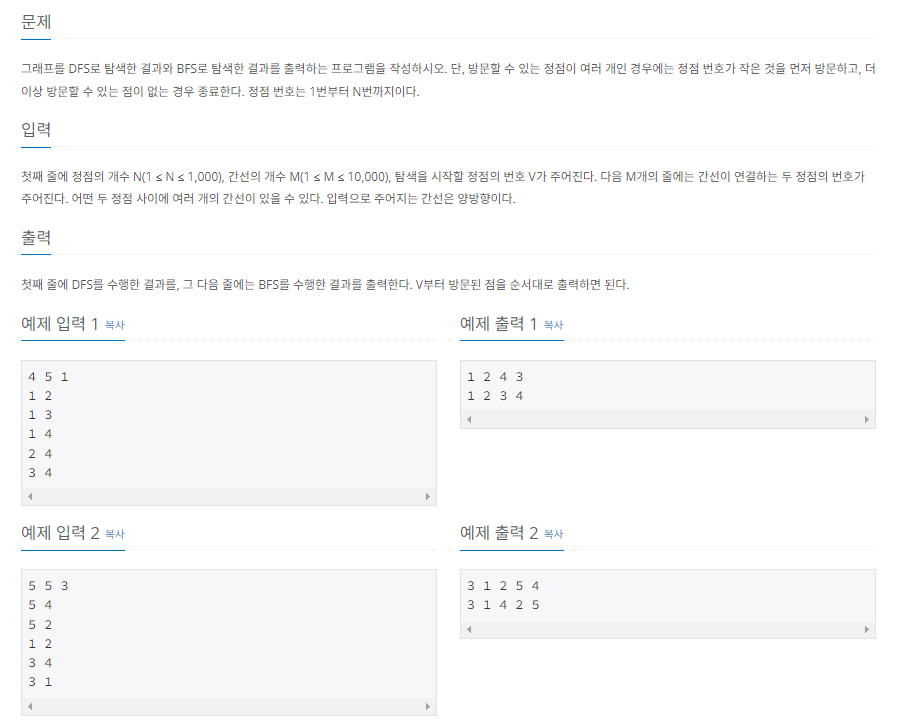
이번 포스팅에서는 BFS/DFS, 이진 탐색, 트리 순회에 대한 개념적인 문제만 풀어보기로 하고, 나중에 그래프 자료구조를 학습한 이후에 본격적인 실전 문제를 풀어보도록 하겠습니다.

1. Binary Search

1) 개념

이진 탐색의 특징은 아래와 같다.

• 리스트가 정렬되어 있다.
• 탐색 범위가 절반씩 줄어드는 O(logN) 알고리즘이다.

탐색 범위를 절반으로 좁히는 방법은 간단하다. 리스트의 시작점과 끝점을 start와 end로 두고, 중간지점을 mid로 둔다(여기서는 mid를 내림으로 계산함).

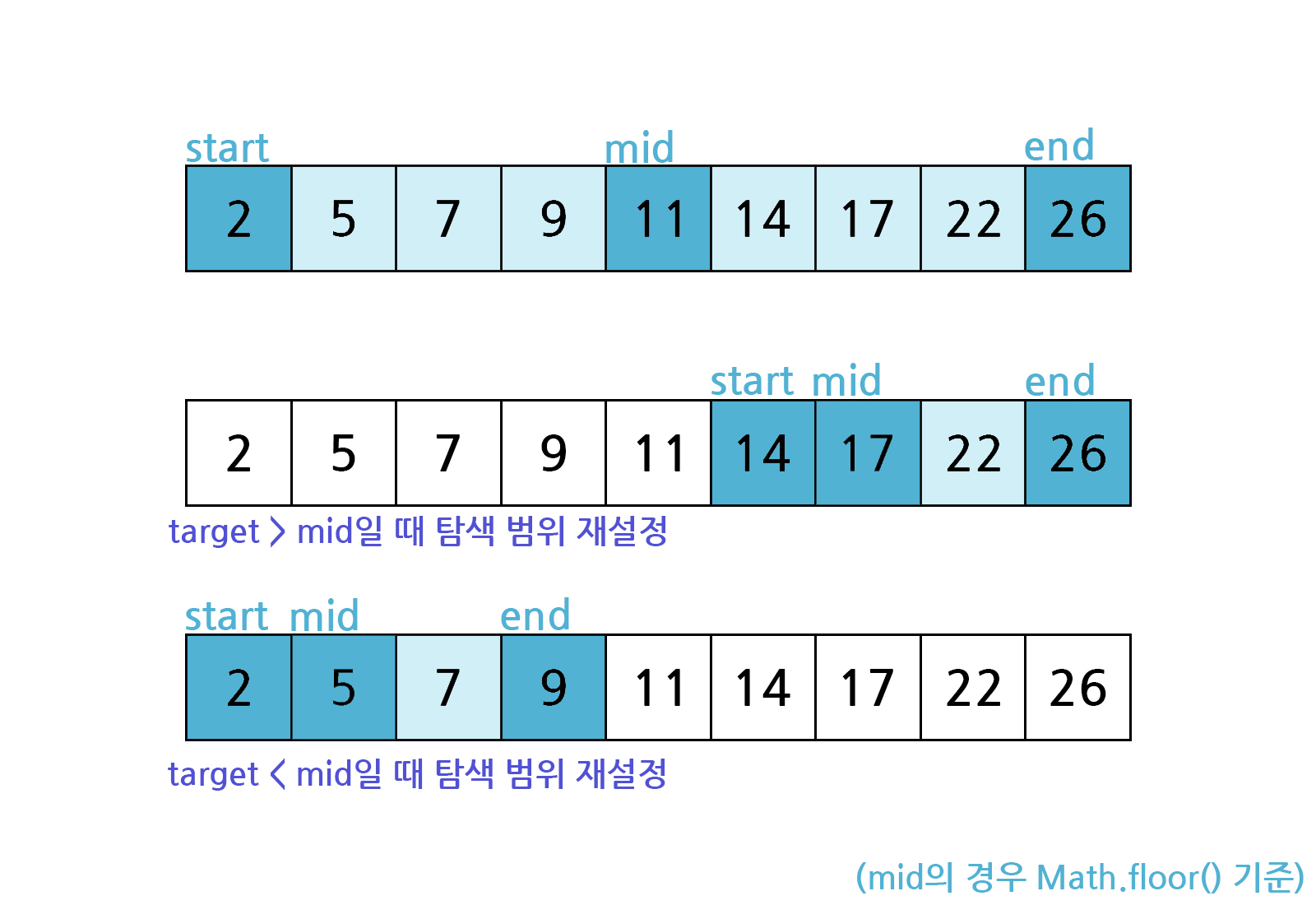
이진탐색에서 값을 찾는 경우는 아래의 두 가지뿐이다.

• 우연히 mid 값이 찾는 값과 동일한 경우
• start, end 값이 동일한 경우(mid 값도 동일)

즉, start <= end일 때까지 절반씩 나누어 탐색하는 과정을 반복하고, start > end 까지 원하는 값을 찾지 못했으면, -1을 반환하는 방식으로 이진 탐색을 구현할 수 있다.

2) 구현

매개변수로 전달된 리스트는 이미 정렬되어 있다고 가정한다. 아래의 틀을 암기해두고 있으면, 이진 탐색이 필요한 문제에 유용하게 활용할 수 있을 것이다.

def binary_search(lst, target):
	start = 0
    end = len(lst) - 1
    while start <= end:
    	mid = (start + end) // 2 # 소수점 이하 버림
        if lst[mid] == target:
        	return mid
        elif lst[mid] < target:
        	start = mid + 1
        else:
        	end = mid - 1
            
    return -1    	

3) 예제

>> 백준 1920번

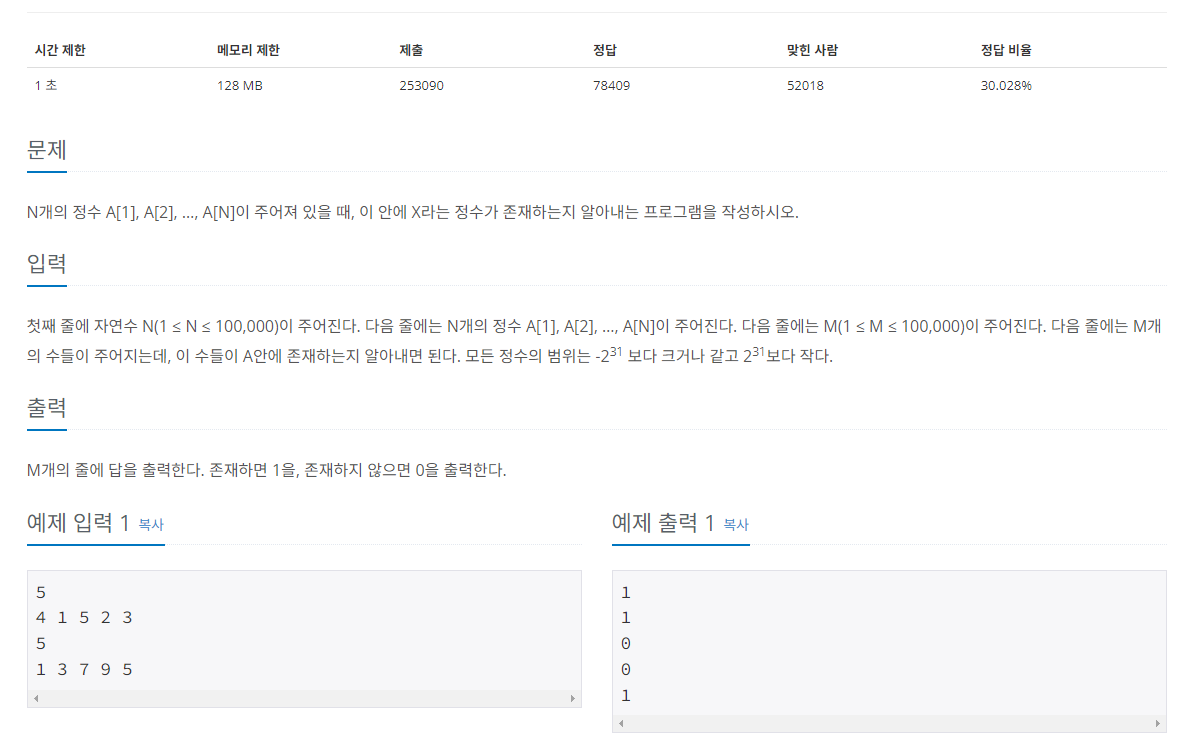
위 문제를 이중 for문으로 풀이하면 시간 초과가 발생할 것으로 예상되므로, 위에서 배운 이진 탐색을 그대로 활용하기로 한다.

import sys
input = sys.stdin.readline

def binary_search(lst, target):
    start = 0
    end = len(lst) - 1

    while start <= end:
        mid = (start + end) // 2
        if lst[mid] == target:
            return mid
        elif lst[mid] < target:
            start = mid + 1
        else:
            end = mid - 1

    return -1

N = int(input())
A = list(map(int, input().split()))
M = int(input()) 
X = list(map(int, input().split()))

A.sort()

for i in X:
    result = binary_search(A, i)
    if result != -1:
        print(1)
    else:
        print(0)

기본 파트에서 다루기는 조금 앞선 내용이기는 하지만, 집합 자료구조에 대해 이해하고 있는 사람이라면, 아래와 같은 풀이가 더 익숙할 것이다.

import sys
input = sys.stdin.readline

N = int(input())
S = set(map(int, input().split()))

M = int(input())
lst = list(map(int, input().split()))

for i in lst:
    if i in S:
        print(1)
    else:
        print(0)

2. BFS(Breadth-First Search) / DFS(Depth-First Search)

1) 개념

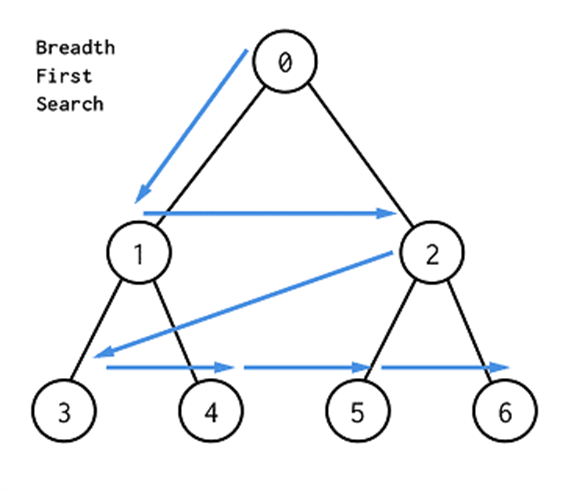
① BFS

• 시작 노드에 인접한 노드를 우선적으로 탐색
• 인접한 노드에 모두 방문한 이후에는 가장 가까운 레벨의 노드를 탐색
• Queue(Deque) 자료구조를 이용하여 구현

② DFS

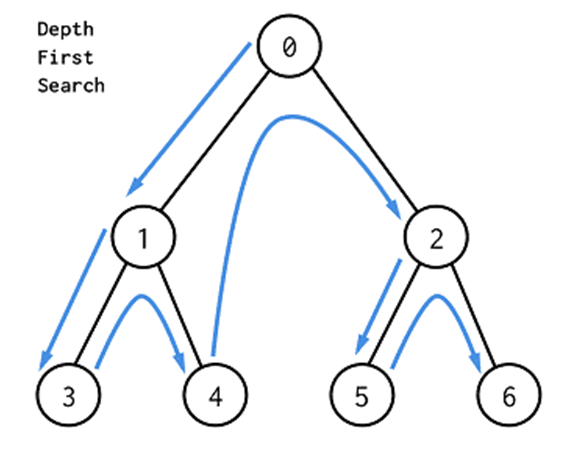
• 시작 노드부터 다음 레벨의 노드 방향으로 가능한 멀리까지 탐색
• 더 이상 진행할 수 없는 경우 이전에 방문한 노드로 되돌아간 후 다시 가능한 멀리까지 탐색
• Stack 자료구조를 이용하여 구현

2) 사전 지식

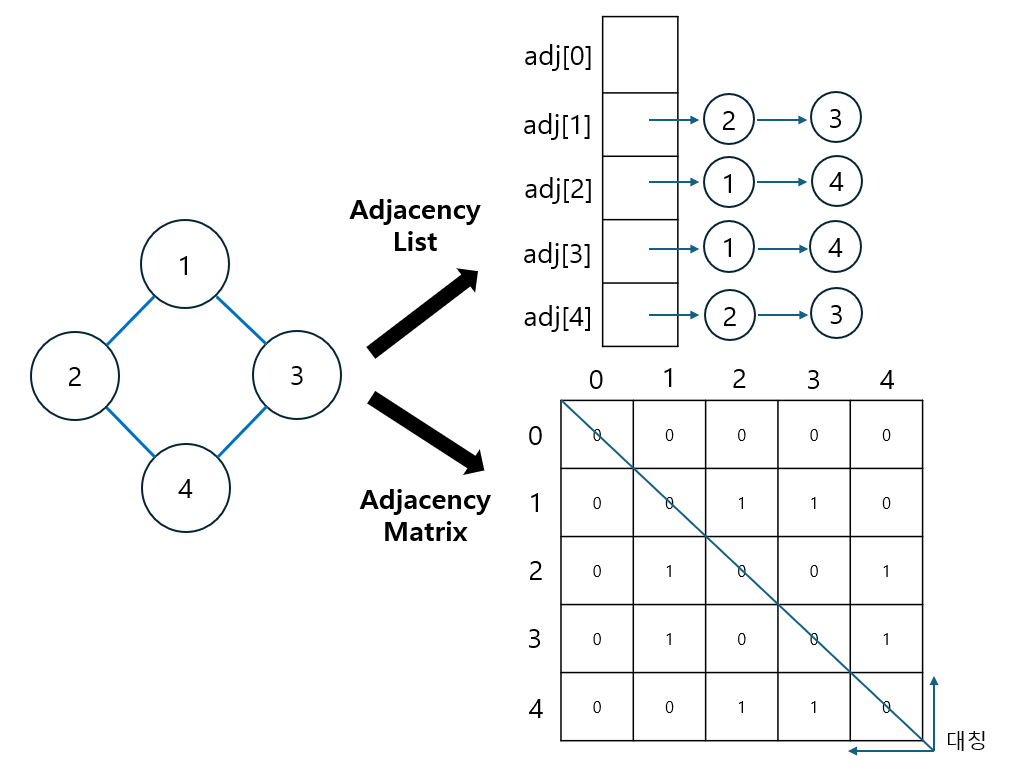
Adjacency List 또는 Adjacency Matrix를 사용하여, 그래프의 노드들이 어떻게 연결되어 있는지를 저장할 수 있다.

① Adjacency List

• 장점
  • 간선의 수에 비례하는 저장 공간만을 필요로 한다.
  • 특정 노드와 연결된 노드를 빠르게(실제 연결된만큼만 확인하면 됨) 확인할 수 있다.
• 단점
  • 노드 간의 연결 여부를 알아내기 위해 해당 노드의 인접 리스트 전체를 순회해야 한다.

② Adjacency Matrix

• 장점
  • 구현이 단순하다.
  • 노드 간의 연결 여부를 O(1) 시간만에 확인할 수 있다.
• 단점
  • 노드 수에 비례하여 메모리를 차지하므로, 노드에 비해 간선이 적을 경우 저장 공간을 비효율적으로 사용하게 된다.
  • 특정 노드와 연결된 노드를 확인하는 데에 노드 개수에 비례하는 시간이 소요된다.

3) 예제

>> 백준 1260번

BFS, DFS를 사용하기 위해 저장해야 하는 정보는 아래의 두 가지이다.

① 각 정점과 연결된 정점

• 위에서 설명한 Adjacency List 또는 Adjacency Matrix를 이용해 저장할 수 있다.
• 여기서는 구현이 단순한 Adjacency Matrix를 이용하기로 한다.

## List Comprehension 형태로 이차원 행렬 생성
N, E, V = map(int, input().split()) # N은 노드의 수, E는 간선의 수, V는 시작 노드의 번호
graph = [[0]*(N+1) for _ in range(N+1)] # 0번 행과 열을 비워두기 위해 N+1 크기로 생성, 기본 값 0은 연결되지 않음을 의미

## 노드 연결하기 ex) 1번 노드와 2번 노드 연결
graph[1][2] = graph[2][1] = 1 # 0과 1로 연결 여부 구분

② 어떤 정점을 방문했는지 리스트에 저장

• BFS는 Queue에, DFS는 Stack에서 노드를 관리한다.
• 스택이나 큐에 노드가 append 되면, 이는 해당 노드를 방문했음을 의미하는 것이므로, visited 배열에 방문한 적이 있음을 저장해야 한다.

visited = [0]*(N+1) # 1번 노드에 방문했다면, 1번 인덱스의 원소를 1로 업데이트함

위의 내용을 바탕으로, BFS와 DFS를 구현해보자. 참고로 DFS는 Stack을 명시적으로 사용하는 대신 재귀 호출을 이용하도록 하겠다.

※ Stack을 사용하지 않는 이유
Stack을 사용하는 알고리즘은 대부분 재귀 호출을 사용하는 방식으로 대체할 수 있다. 그 이유는 재귀 호출이 내부적으로 호출 스택을 사용하기 때문이다. Stack을 명시적으로 사용할 때보다 재귀 호출을 사용할 때, 코드의 간결성과 가독성이 더 높기 때문에 재귀 호출로 구현하는 방법이 권장된다.

import sys 
from collections import deque
input = sys.stdin.readline

def bfs(V):
    deq = deque()
    deq.append(V) # 시작 노드 방문
    visited1[V] = 1 # 방문 표시
    while deq:
        V = deq.popleft()
        print(V, end=' ')
        for i in range(1, N+1): 
            if graph[V][i] == 1 and visited1[i] == 0  : # 인접 노드 중 방문하지 않은 노드를 큐에 append()
                deq.append(i)
                visited1[i] = 1

def dfs(V):
    visited2[V] = 1
    print(V, end=' ')
    for i in range(1, N+1):
        if graph[V][i] == 1 and visited2[i] == 0  : # 인접 노드 중 방문하지 않은 노드를 stack에 append()하고 해당 노드 기점으로 끝까지 반복
            dfs(i)


N, M, V = map(int, input().split())
graph = [[0] * (N + 1) for _ in range(N + 1)]

## 각 정점과 연결된 정점을 이차원 행렬에 저장
for i in range(M):
    a, b = map(int, input().split())
    graph[a][b] = graph[b][a] = 1

## 어떤 정점을 방문했는지 리스트에 저장
visited1 = [0] * (N+1) # BFS 방문 배열
visited2 = [0] * (N+1) # DFS 방문 배열

dfs(V)
print()
bfs(V)

3. Tree Traversal

1) 개념

트리에서의 깊이 우선 탐색은 전위(Pre-Order), 중위(In-Order), 후위(Post-Order) 순회로 구분된다. 여기서 전위, 중위, 후위는 Root 노드의 위치를 의미하는 것이며, 항상 우측보다 좌측을 먼저 순회한다.

• 전위 순회: Root-Left-Right

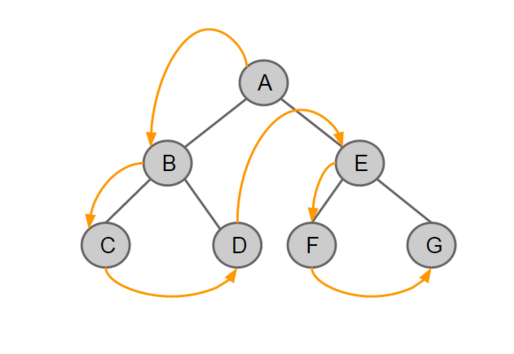
• 중위 순회: Left-Root-Right

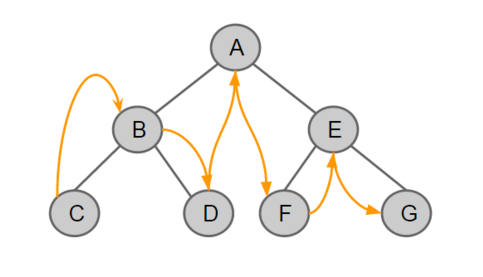
• 후위 순회: Left-Right-Root

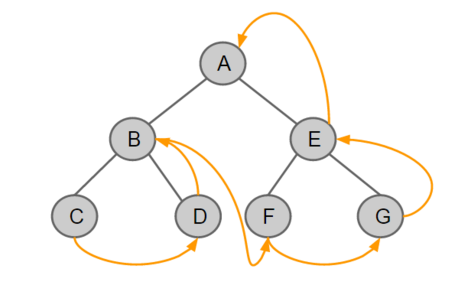
2) 예제

이번에는 문제를 바로 풀어보면서 Binary Tree를 전위, 중위, 후위 순회하는 방법에 대해 알아보기로 하겠다.
>> 백준 1991번

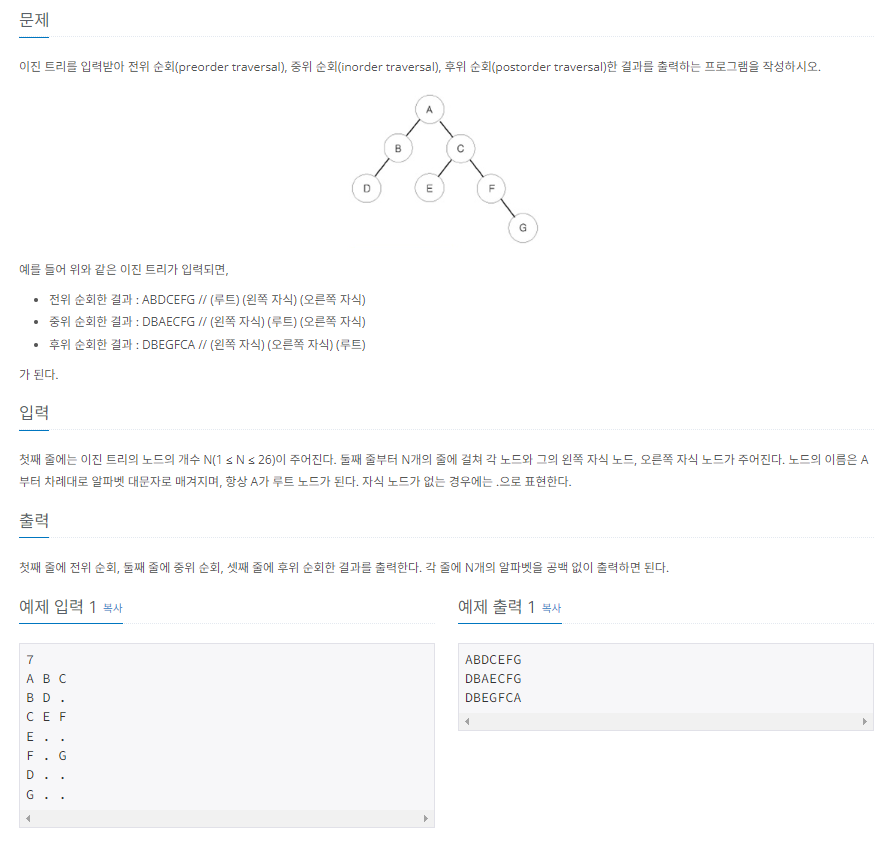
위 문제를 풀이하는 기본 전략은 Tree를 Dictionary로 구현하여 Key에는 Root(Parent) 노드를, Value에는 [L 노드, R 노드]를 할당하는 것이다. 그리고 Root 노드가 존재하지 않을 때까지 재귀 호출하는 방식으로 전위, 중위, 후위 순회를 구현한다. 재귀 호출을 사용하는 이유는 전위, 중위, 후위 순회가 모두 DFS의 일종이기 때문이다.

import sys
input = sys.stdin.readline
 
N = int(input())
tree = {} # 딕셔너리
 
for i in range(N):
    root, left, right = input().split()
    tree[root] = [left, right]
 
 
def preorder(root): # 전위 순회
    if root != '.':
        print(root, end='')  # root
        preorder(tree[root][0])  # left
        preorder(tree[root][1])  # right
 
 
def inorder(root): # 중위 순회
    if root != '.':
        inorder(tree[root][0])  # left
        print(root, end='')  # root
        inorder(tree[root][1])  # right
 
 
def postorder(root): # 후위 순회
    if root != '.':
        postorder(tree[root][0])  # left
        postorder(tree[root][1])  # right
        print(root, end='')  # root
 
 
preorder('A')
print() # 줄바꿈
inorder('A')
print()
postorder('A')