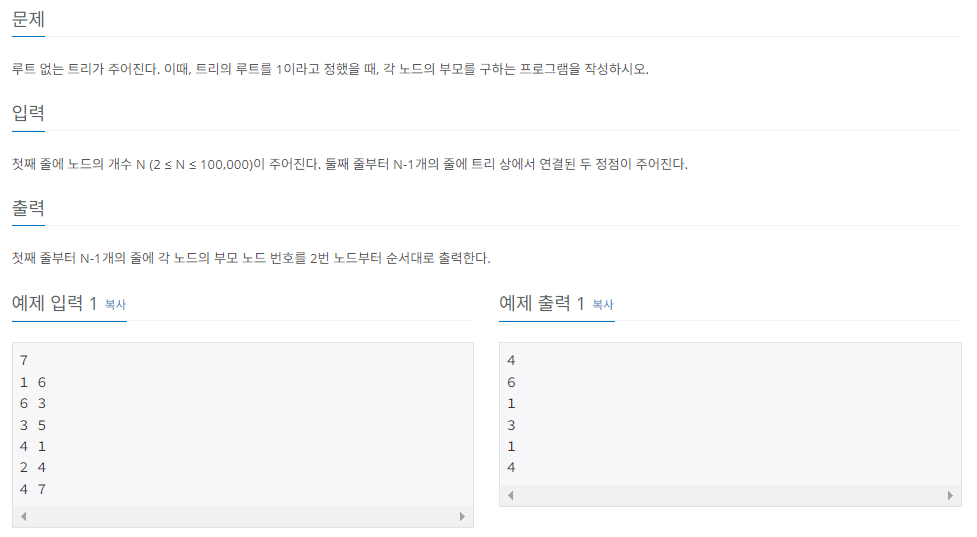
1. 트리의 부모 찾기
문제의 입력이 간선 형태인 것으로 보아, 인접 리스트를 이용해 트리를 표현해야 할 것이며, 노드 간의 상하 관계를 알 수 없으므로 양방향 간선으로 간주하여 풀이해야 할 것이다.
다음으로 각 노드의 부모 노드를 알아내기 위해, 트리 탐색 알고리즘을 선택해야 한다. 부모 노드의 인접 노드가 곧 자식 노드라는 점을 이용하여 BFS를 사용할 수도 있고, 노드 간 하향 연결을 확인하는 문제라는 점에서 DFS를 사용할 수도 있다. 여기서는 DFS를 이용해 풀이할 것이다. (BFS/DFS를 모두 사용해도 되는 문제인 경우, 재귀함수로 구현을 단순화할 수 있는 DFS를 사용하는 것이 일반적이다.)
import sys
sys.setrecursionlimit(10 ** 8)
input = sys.stdin.readline
N = int(input())
# 인접 리스트를 이용한 트리 표현
tree = [[] for i in range(N + 1)]
visited = [0] * (N + 1) # 방문 배열
parent = [0] * (N + 1) # 각 노드의 부모 노드
def dfs(V):
visited[V] = 1 # a방문 표시
for i in tree[V]: # 인접 노드 탐색
if visited[i] == 0:
parent[i] = V
dfs(i)
for i in range(N - 1):
u, v = map(int, input().split())
tree[u].append(v)
tree[v].append(u) # 양방향 간선
dfs(1)
for i in range(2, N + 1):
print(parent[i])2. 리프 노드의 개수 구하기
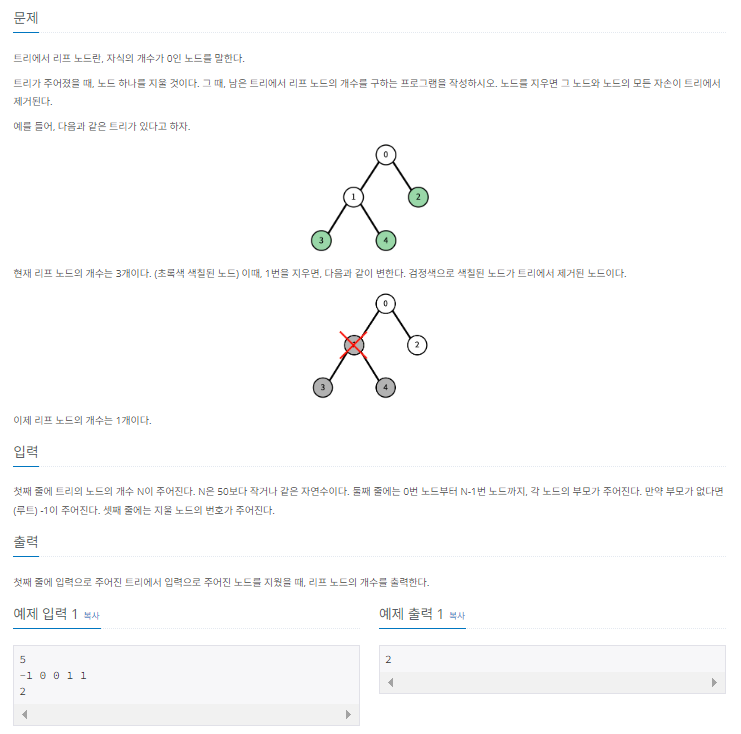
문제의 입력이 배열 형태이긴 하지만, 완전 이진 트리라는 조건이 없으므로 배열을 이용한 트리 표현은 사용할 수 없다. 대신 주어진 값이 각 노드의 부모 노드이므로, 사실상 간선이 주어진 것이나 마찬가지이다. 따라서, 이번에도 인접 리스트를 이용한 트리 표현을 사용하기로 한다.
위 문제에선 간선 사이의 상하 관계가 명확하므로, 단방향 간선으로 구현할 수 있다. 이 때, 반드시 단방향 간선의 방향은 부모 노드 → 자식 노드가 되어야 한다. 이 방향은 절대 바뀌어서는 안 되기 때문에, 만약 이 부분이 헷갈린다면 양방향 간선으로 구현해도 무방하다.
리프 노드의 개수를 구하려면, 트리를 탐색하면서 자식 노드가 없는 노드의 수를 세어야 한다. BFS를 사용해서 푸는 것도 가능은 하겠지만, 노드 탐색 방향이 명확히 하향이므로, DFS로 구현하기로 한다.
import sys
sys.setrecursionlimit(10 ** 8)
input = sys.stdin.readline
N = int(input())
parent = list(map(int, input().split()))
delNode = int(input())
# 인접 리스트를 이용한 트리 표현
tree = [[] for i in range(N)]
visited = [0] * (N) # 방문 배열
cnt = 0 # 리프 노드의 개수
for i in range(N):
if parent[i] != -1:
tree[parent[i]].append(i) # 상하 관계가 명확하므로, 단방향 간선으로 구현
else:
root = i # 루트 노드 저장
def dfs(V):
global cnt # 외부 변수 cnt를 조작하기 위해 전역변수화
visited[V] = 1 # 방문 표시
hasChild = False
for i in tree[V]:
if visited[i] == 0 and i != delNode: # delNode에 대해서는 dfs를 수행하지 않음
hasChild = True
dfs(i)
if not hasChild: # 자식 노드가 없으면 리프 노드로 간주
cnt += 1
if delNode == root: # root 노드가 삭제될 때, cnt가 1로 계산되는 예외를 방지
print(0)
else:
dfs(root)
print(cnt)위 문제에서 실수하기 쉬운 부분은 마지막 if delNode == root: 부분에 대한 예외 처리이다. 삭제된 노드에 대해서는 dfs를 수행하지 않기 때문에 root가 지워져도 제대로 동작할 것이라 생각하기 쉽지만, root 노드가 지워질 경우 hasChild가 False가 되면서 리프 노드의 개수가 1로 계산되는 예외가 발생한다. 따라서, root 노드가 삭제되는 경우에 대한 처리 로직이 반드시 필요하다.