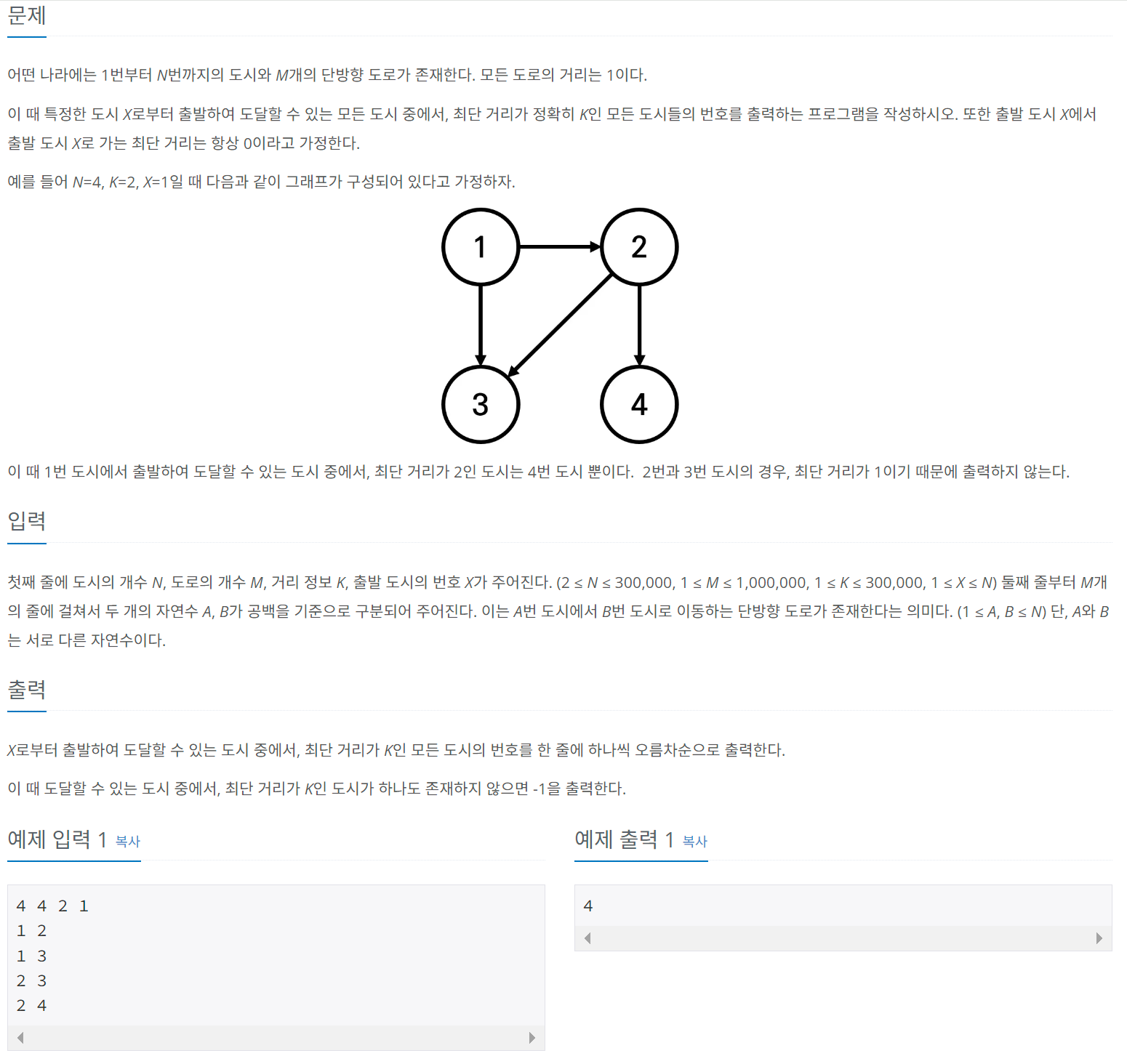
그래프 자료구조에 대해 학습하기 전, Tree 자료구조에 대한 포스팅을 먼저 참조해주시기 바랍니다.
>> 자료구조 기본 - Tree
1. 그래프의 표현
Tree 자료구조를 학습할 때 배웠던 인접행렬과 인접리스트에 대해 다시 한번 복습해보기로 하자.
1) 2차원 배열 생성하기
그래프를 구현하기 위해선 먼저 2차원 배열을 생성할 수 있어야 한다. 이 때, 2차원 배열은 List Comprehension을 이용하여 생성할 것을 권장한다.
# 3행 4열의 2차원 행렬 생성
matrix = [[0 for col in range(4)] for row in range(3)]주의해야 할 것은 아래와 같은 방식으로 2차원 배열을 생성해선 안 된다는 것이다.
matrix = [[0] * 4] * 3] # [0, 0, 0, 0] 배열 3개가 복사되는 형태 위 방식은 Shallow Copy를 이용해 배열을 생성하므로, matrix[0][0]이 1로 수정될 때, matrix[1][0]과 matrix[2][0]도 1로 수정되는 문제가 발생한다.
2) Edge List
Edge List는 간선을 중심으로 그래프를 표현하는 방법이다.
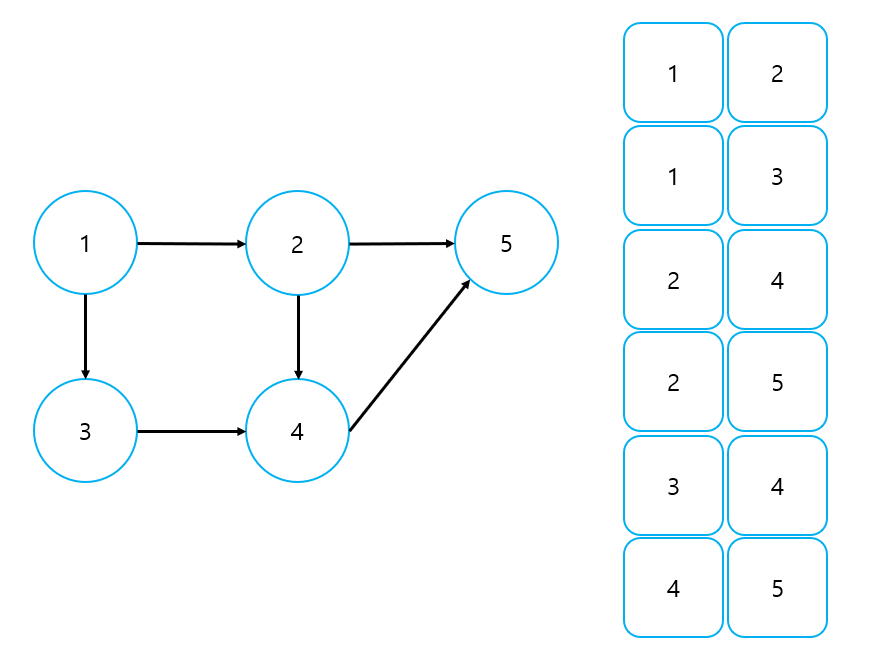
① 가중치가 없는 그래프
- 출발 노드, 도착 노드를 저장한다,
- 간선은 [출발, 도착]의 형태로 표현된다. ex) [1, 2]
- 행의 개수는 간선의 개수와 같고, 열의 개수는 2이다.
- 무향 그래프의 경우, 상황에 따라 [출발, 도착], [도착, 출발]을 모두 저장해야 할 수도 있고, [출발, 도착]만 저장해야 할 수도 있다.
② 가중치가 있는 그래프
- 출발 노드, 도착 노드, 가중치를 저장한다.
- 간선은 [출발, 도착, 가중치]의 형태로 표현된다. ex) [1, 2, 6]
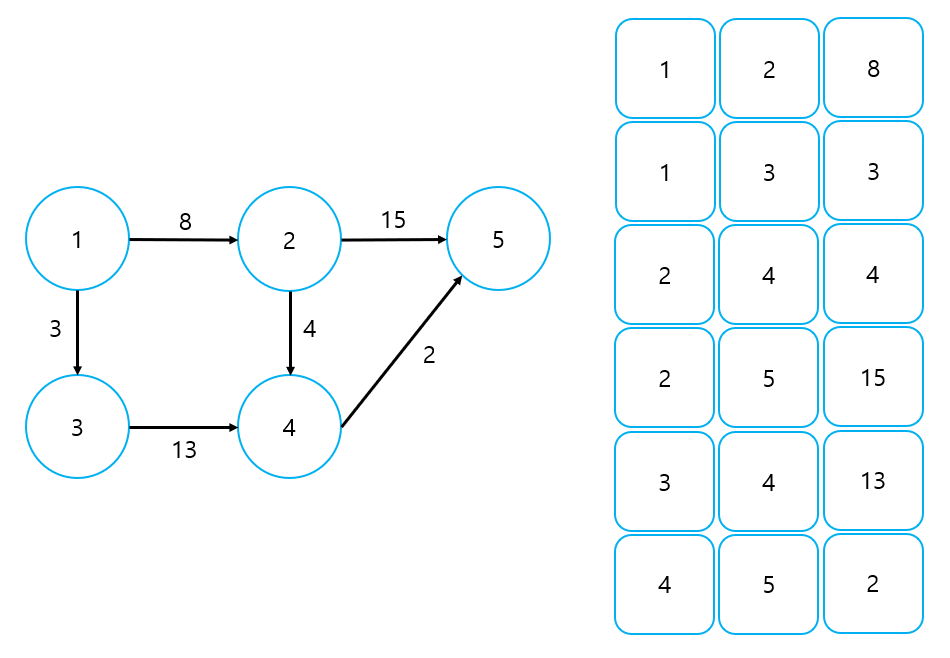
Edge List는 구현이 쉽다는 장점이 있지만, 특정 노드에서 뻗어 나가는 간선(인접 노드)을 파악하기에는 어려움이 있다. 그러다보니 Edge List는 노드를 중심으로 하는 알고리즘에는 거의 사용되지 않고, 주로 노드 사이의 최단 거리를 구하는 Bellman-Ford 알고리즘이나 Kruskal 알고리즘에 사용된다.
3) Adjacency Matrix
Edge List와 달리 Adjacency Matrix는 노드 중심의 그래프 표현이다. Adjacency Matrix에 대해서는 이미 설명한 적이 있기 때문에 자세한 설명은 생략하기로 한다.
① 가중치가 없는 그래프
- 0은 간선이 존재하지 않음을, 1은 간선이 존재함을 의미한다.
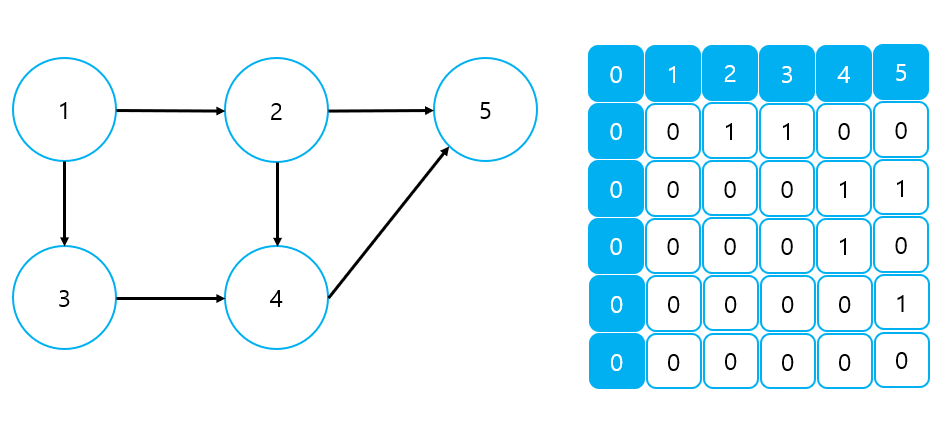
② 가중치가 있는 그래프
- 간선이 존재하는 경우, 해당 간선의 가중치를 저장한다.
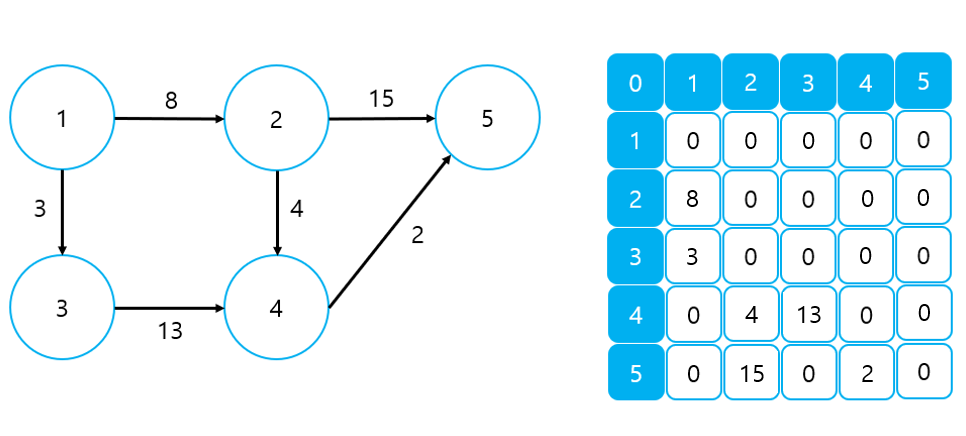
참고로, 무향 그래프의 경우 Adjacency Matrix는 항상 대칭 형태를 띄게 된다. Adjacency Matrix는 구현이 단순하고, 노드 간 연결 상태 및 가중치를 쉽게 확인할 수 있다는 장점이 있다. 하지만, 공간 활용이 비효율적이며 특정 노드의 인접 노드를 바로 파악하기 어렵다는 것은 단점이다.
4) Adjacency List
Adjacency List도 바로 그림으로 살펴보기로 하자.
① 가중치가 없는 그래프
- [[] for _ in range(N + 1)]의 2차원 배열을 생성한 후 연결된 노드를 append 하는 방식으로 표현
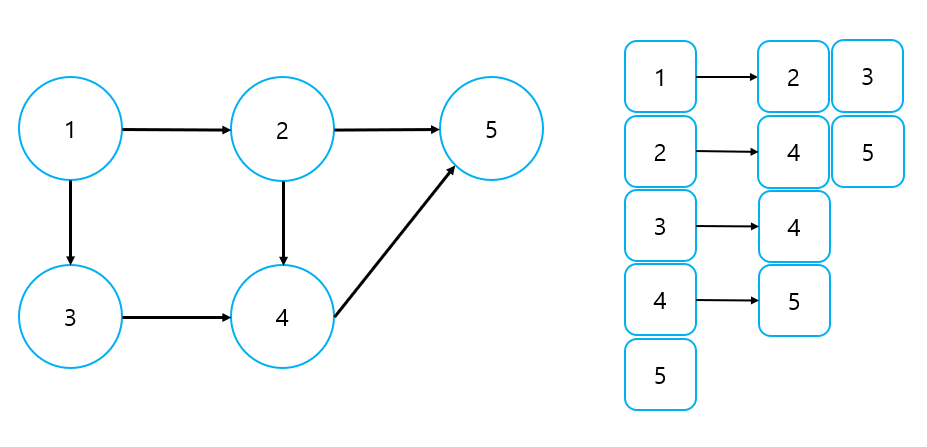
② 가중치가 있는 그래프
- 연결된 노드 번호와 더불어 가중치를 함께 append 하는 방식으로 표현
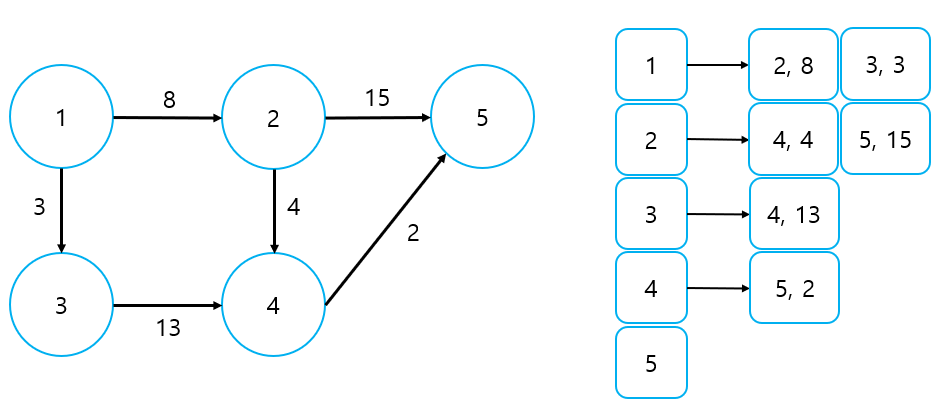
Adjacency List는 다른 방법에 비해 구현 난이도가 높다. 대신 특정 노드에서 뻗어나가는 간선을 파악하기에는 매우 용이하고, 공간 효율도 매우 높다. 구현이 어렵지만 성능이 높은만큼, 간혹 어떤 문제에서는 메모리 제약을 타이트하게 걸어 인접 리스트를 이용한 풀이를 유도하기도 한다.
2. 문제 풀이
1) 특정 거리의 도시 찾기
위 문제를 풀이하기 위해 적절한 그래프 표현 방식은 무엇일까? 먼저 Edge List의 경우, 특정 노드의 인접 노드를 알아내기 어려운 구조이기 때문에 위 문제 풀이에는 적합하지 않을 것 같다.
다음으로, 인접 행렬과 인접 리스트 중에 선택해야 하는데, 이러한 경우에는 시간 복잡도를 고려해야 한다. 그래프를 순회하기 위해서는 BFS 또는 DFS를 사용해야 하므로, 먼저 인접 행렬과 인접 리스트에서 BFS와 DFS를 사용할 때의 시간 복잡도를 알아보자. (Node의 개수를 V, 간선의 개수를 E라 하자.)
① 인접 행렬
- 특정 노드가 어떤 노드와 인접해있는지 검사하기 위해 모든 노드를 순회하는 작업을, 모든 노드에 대해 반복해야 한다.
- 따라서, 시간 복잡도는
O(V^2)이 된다.
② 인접 리스트
- 각 노드마다 연결된 정점을 방문하는 작업이 반복되는데, 이 때 연결된 정점을 방문하는 총 횟수는 간선의 개수와 같고, 이를 모든 노드에 대해 반복해야 한다.
- 따라서, 시간 복잡도는
O(V + E)가 된다.
위 문제에서 주어진 노드의 최대 개수는 300,000이고 간선의 최대 개수는 1,000,000이며, 시간 제한은 2초이다. 만약 인접 행렬을 사용하는 방식으로 위 문제를 풀이할 경우, 300,000 ^ 2 = 9 * 10 ^ 10이므로, 시간 초과가 발생할 것이다. 반면, 인접 리스트를 이용한 풀이의 경우 1,000,000 + 300,000 = 1,300,000이므로, 시간 제약을 여유롭게 만족할 수 있을 것이다.
그렇다면 마지막으로, BFS와 DFS 중 어떤 방법으로 그래프를 순회해야 할까? 결론부터 이야기하면, 가중치가 없는 그래프에서 노드 간 최단 거리를 찾는 문제는 항상 BFS를 사용하는 것이 유리하다. 그 이유는 BFS가 시작 노드로부터 가까운 노드를 우선적으로 탐색하기 때문이다. 따라서, 가중치가 없는 경우에 한해 BFS는 노드 간의 최단 경로를 보장할 수 있다. 반면, DFS는 출발 노드로부터 최대한 깊이 있게 탐색하는 것이 목적이므로, 최단 거리를 찾기 위한 알고리즘으로는 적절하지 않다. 따라서, 위 문제는 인접 리스트와 BFS를 이용하여 풀이할 수 있을 것이다.
import sys
from collections import deque
input = sys.stdin.readline
N, M, K, X = map(int, input().split())
arr = [[] for _ in range(N + 1)] # 노드(도시) 번호가 1부터 시작하므로 N + 1까지 생성
for i in range(M): # 인접 리스트 생성
A, B = map(int, input().split())
arr[A].append(B)
# visited 배열의 원소가 0 이상일 경우, 이는 방문한 노드임과 동시에 그 값이 출발 노드로부터의 거리임을 의미함.
visited = [-1] * (N + 1) # 모든 노드를 미방문 상태로 초기화
def bfs(V):
deq = deque()
deq.append(V)
visited[V] = 0 # 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0임.
while deq:
V = deq.popleft()
for i in arr[V]:
if visited[i] == -1: # 미방문 노드
deq.append(i) # 방문한 노드를 deq에 append
visited[i] = visited[V] + 1 # 출발 노드로부터 V까지의 거리 + 1
bfs(X)
answer = [] # 조건을 만족하는 노드 번호를 오름차순으로 출력하기 위한 배열
for i in range(N + 1):
if visited[i] == K:
answer.append(i)
if not answer:
print(-1)
else:
print('\n'.join(map(str, answer)))이처럼 가중치가 없는 그래프에서의 최단 거리는 BFS로 구할 수 있지만, 만약 가중치가 존재할 경우 나중에 배울 다익스트라 알고리즘으로 풀이해야 한다. (아직 배우지 않은 내용이므로, 참고만 하기 바란다.)
import sys
input = sys.stdin.readline
from queue import PriorityQueue
N, M, K, X = map(int, input().split())
graph = [[] for i in range(N + 1)]
visited = [0] * (N + 1)
dist = [sys.maxsize for i in range(N + 1)]
dist[X] = 0
for i in range(M):
u, v = map(int, input().split())
graph[u].append((1, v))
def dijkstra(start):
pq = PriorityQueue()
pq.put((0, start))
while not pq.empty():
node = pq.get()
num = node[1]
if visited[num] == 0:
visited[num] = 1
for i in graph[num]:
weight = i[0]
next = i[1]
dist[next] = min(dist[next], dist[num] + weight)
pq.put((dist[next], next))
dijkstra(X)
answer = []
for i in range(len(dist)):
if dist[i] == K:
answer.append(i)
if not answer:
print(-1)
else:
print('\n'.join(map(str, answer)))2) 이분 그래프 판별하기
이분 그래프란, 아래와 같이 두 가지의 색상만 이용하여 인접한 정점을 서로 다른 색으로 칠할 수 있는 그래프를 의미한다.
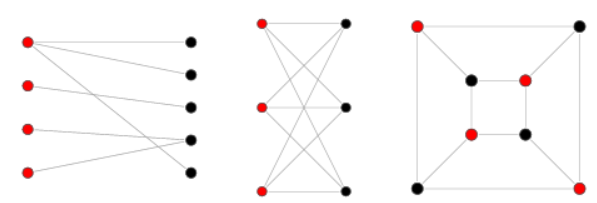
이분 그래프를 판별할 때에는 DFS를 사용할 수도 있고, BFS를 사용할 수도 있다. 즉, DFS 또는 BFS로 노드를 순회하면서, 인접한 정점이 같은 색으로 칠해지는 경우가 없는지 검사할 것이다.
여기서는 인접 행렬과 인접 리스트 중 어떤 것을 사용해도 시간이 초과되지는 않을 것으로 보인다. (제한 시간 2초) 하지만, 이미 저번 포스팅에서 인접 행렬을 이용한 DFS와 BFS를 다루었기 때문에, 이번에는 인접 리스트에 DFS를 적용하는 방식으로 풀어보기로 하자.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10 ** 6) # 깊은 재귀 호출
def dfs(V, color): # 이분 그래프가 맞는지 여부를 반환하는 메서드
visited[V] = color # 방문한 노드 색칠 (-1 = 빨간색, 1 = 파란색)
for i in graph[V]:
if visited[i] == 0: # 인접한 노드 중 방문하지 않은 노드
if not dfs(i, -color): # 다른 색으로 색칠 불가
return False
elif visited[i] == visited[V] : # 방문한 노드이지만, 색깔이 같은 경우도 이분 그래프가 아님
return False
return True
K = int(input())
for i in range(K):
V, E = map(int, input().split())
visited = [0] * (V + 1) # 노드의 번호를 인덱스에 일치시키기 위해 V + 1까지 생성
graph = [[] for _ in range(V + 1)] # 인접 리스트를 이용한 그래프 표현
for j in range(E):
A, B = map(int, input().split()) # 연결된 노드 쌍
graph[A].append(B) # 무향 그래프
graph[B].append(A)
result = True # 이분그래프인지 확인
for i in range(1, V + 1):
if visited[i] == 0: # 방문한 지점이 아니라면 dfs 실행
result = dfs(i, 1)
if not result:
break
if result:
print("YES")
else:
print("NO")재귀호출을 사용할 때, 한 가지 주의해야 할 것은 sys.setrecursionlimit(10 ** 6)을 반드시 붙여주어야 한다는 것이다. 파이썬의 기본 재귀 깊이 제한은 1000으로, 매우 쉬운 몇몇 문제를 제외하고는 거의 풀 수 없을 정도로 깊이가 얕다.
특히, 코딩 테스트 환경(백준)에서는 재귀 깊이 제한을 초과할 때, 그저 런타임 에러로만 출력되기 때문에, 깊이 제한 설정이 안 되어있음을 인지하지 못할 경우, 억울하게 문제를 틀리게 될 수 있다. 따라서, 재귀 호출을 사용해야 하는 문제에서는 가장 먼저 재귀 깊이 제한을 수동으로 설정할 것을 권장한다.
그럼 재귀 깊이를 어느 정도로 설정해야 할까? 위에서 10 ^ 6을 사용한 이유는 인접 리스트를 사용할 때의 BFS의 시간 복잡도가 2.2 * 10 ^ 5이기 때문이다. 그러나 코딩 테스트 환경에서는 굳이 위와 같이 최적화 할 필요는 없기 때문에, 개인적으로 추천하는 방법은 시간 제약만큼 재귀 깊이를 설정하는 것이다. 예를 들어 시간 제약이 2초라면, 어차피 2억번 이상의 연산이 불가하기 때문에 sys.setrecursionlimit(2 * 10 ** 8)과 같이 설정하면 된다.