1. Union Find
1) 개념
Union Find는 Union 연산과 Find 연산으로 구성된 알고리즘을 말한다. 여기서 각 연산은 아래와 같은 의미를 가진다.
- Union
- 각 노드가 속한 집합을 합집합한다.
- 즉,
union(A, B)는A U B와 같다.
- Find: 특정 노드에 대해 해당 노드가 속한 집합의 대표 노드를 반환한다.
2) 원리
유니온 파인드 알고리즘을 구현하기 위해 1차원 리스트를 사용할 수 있다.
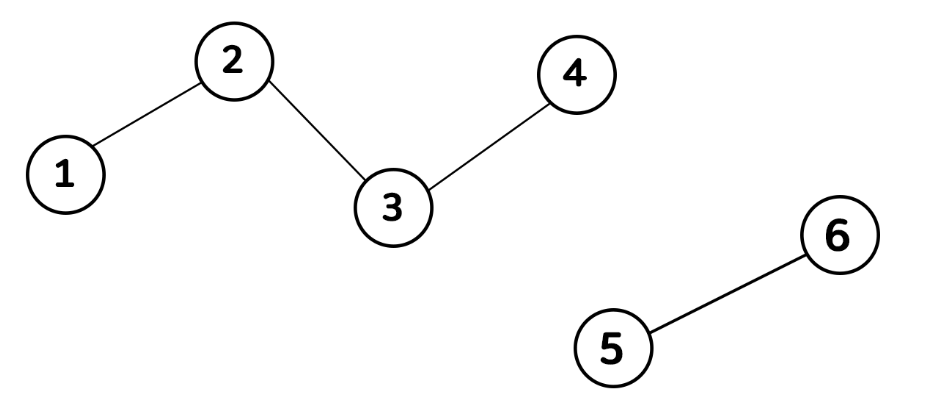
① 초기 상태
- 아래와 같이 1번부터 6번까지의 연결되지 않은 노드가 존재한다고 가정해보자.
- 처음에는 노드 간 연결이 존재하지 않으므로, 각 노드가 곧 집합의 대표 노드가 된다.
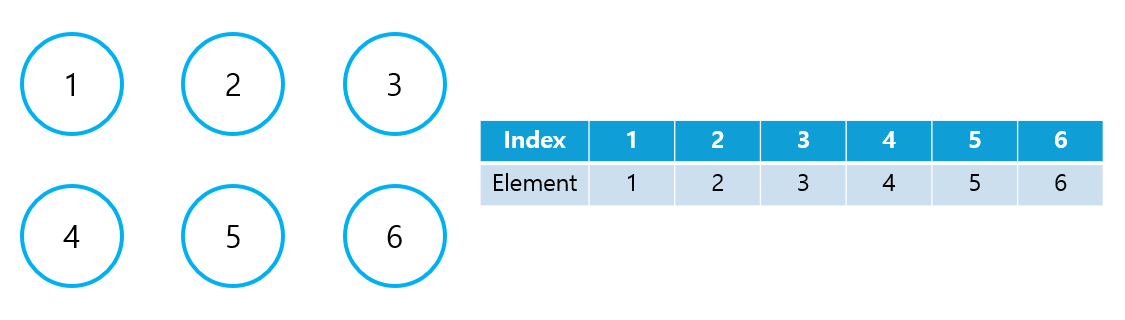
- 즉, 초기 상태의 1차원 리스트는 인덱스 자체를 값으로 갖는 형태를 취하게 될 것이다.
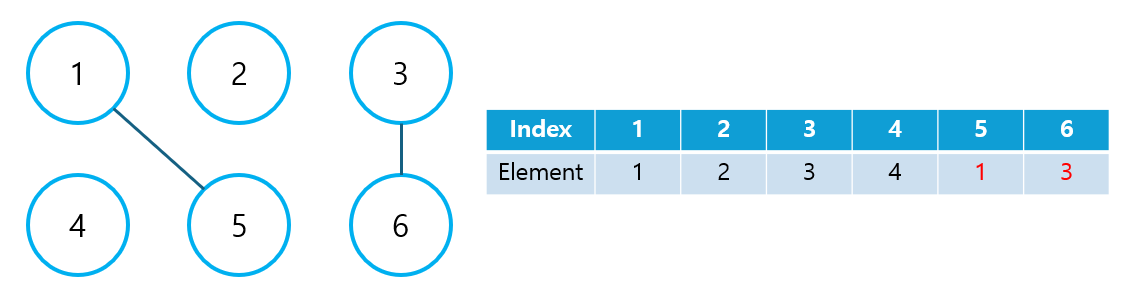
② 비연결 노드 간 Union 연산
- 2개의 노드를 선택해 연결한 후, 자식 노드의 값을 대표 노드의 값으로 업데이트한다.
- 여기서는 1번과 5번, 3번과 6번 노드에 대해 union 연산을 수행한다고 가정한다.
③ 연결 노드 간 Union 연산
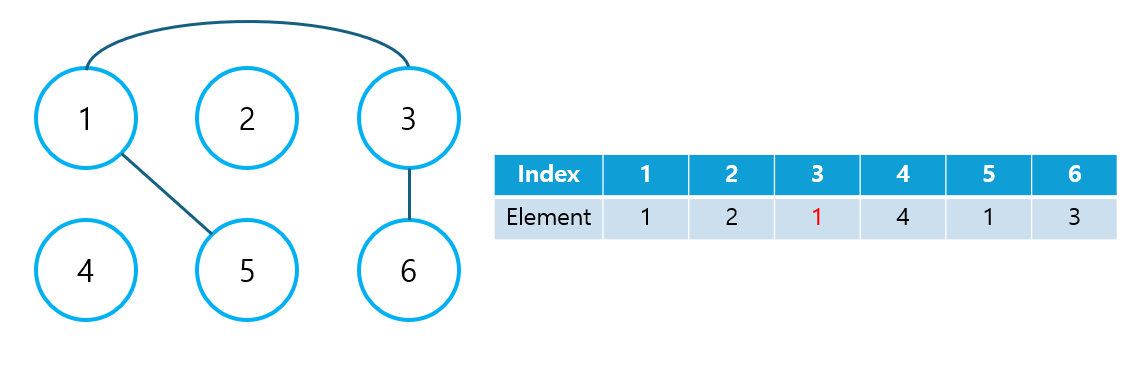
- 이제 5번과 6번 노드에 대해 Union 연산을 수행해보자.
- 이 때 5번과 6번 모두 대표 노드가 아니므로, Find 연산을 이용하여 대표 노드인 1번과 3번 노드를 찾아 연결한다.
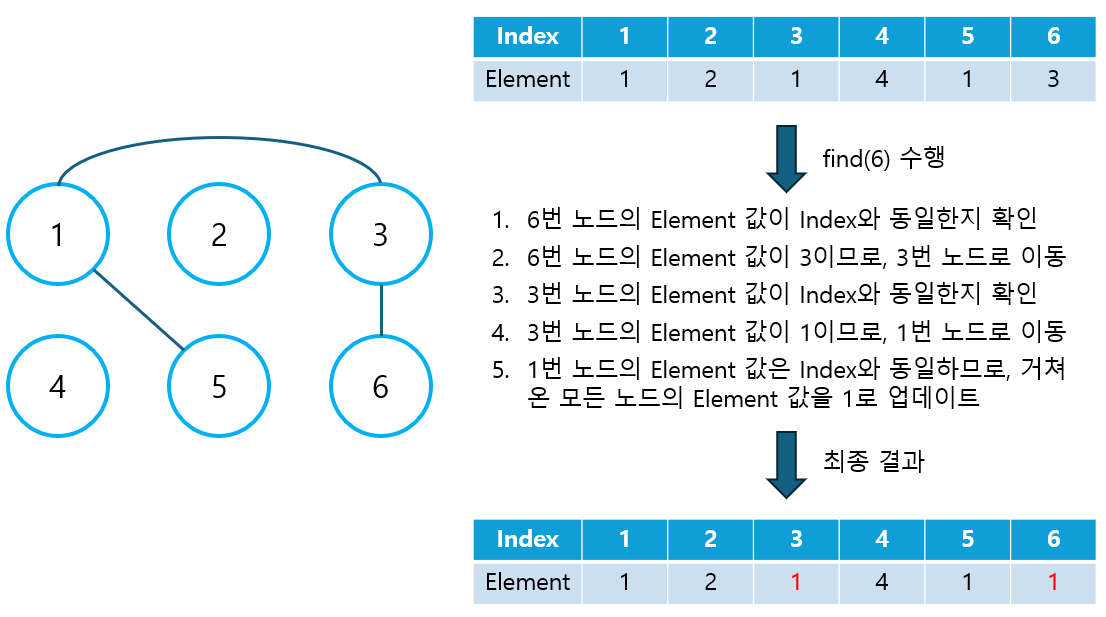
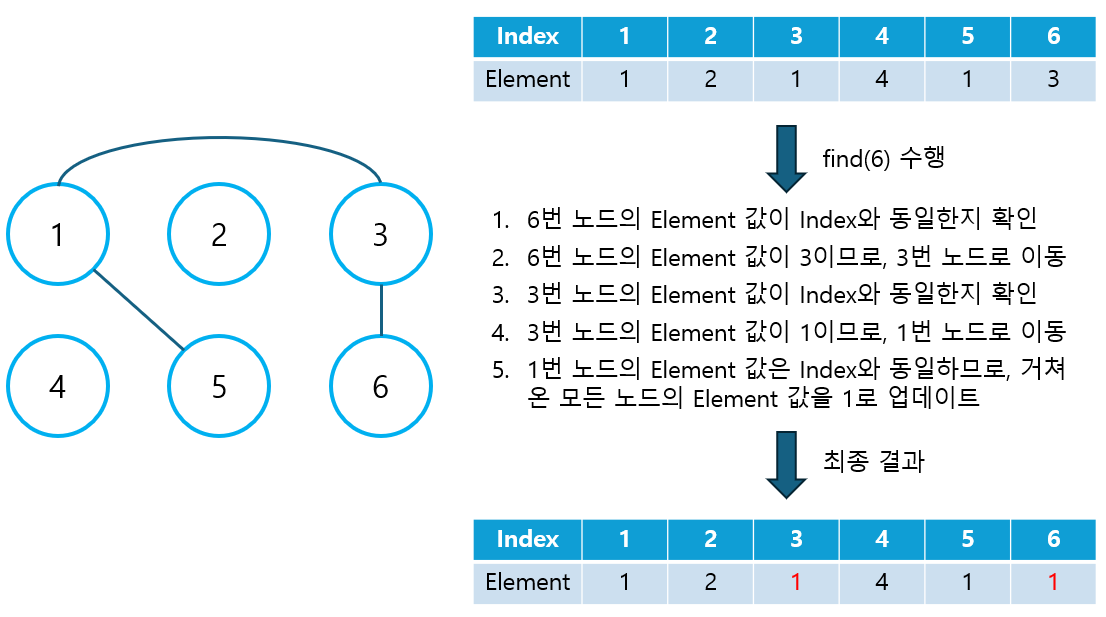
④ Find 연산 구현
- 주어진 노드 번호의 Element 값이 Index와 동일한지 확인한다.
- 동일하지 않은 경우, Element 값에 해당하는 노드로 이동한다.
- Element의 값이 Index 값과 동일해질 때까지 위 과정을 반복(재귀 호출)한다.
- Element의 값이 Index 값과 동일해지면, 이는 대표 노드에 도달했음을 의미하므로, 재귀 함수를 빠져나오면서 거쳐 온 모드 노드의 Element를 대표 노드의 번호로 업데이트한다.
3) Find 연산의 의의
Find 연산은 거쳐온 모든 노드를 대표 노드와 직결시키는 역할을 하는데, 이는 그래프의 연결 상태를 단순화하고, 시간 복잡도를 낮추는 효과가 있다. 1번 ~ 6번 노드가 일렬로 연결되어 있는 그래프를 생각해보자. 이 그래프에 find(6) 연산을 수행할 경우, 그래프가 아래와 같은 형태로 변경된다.
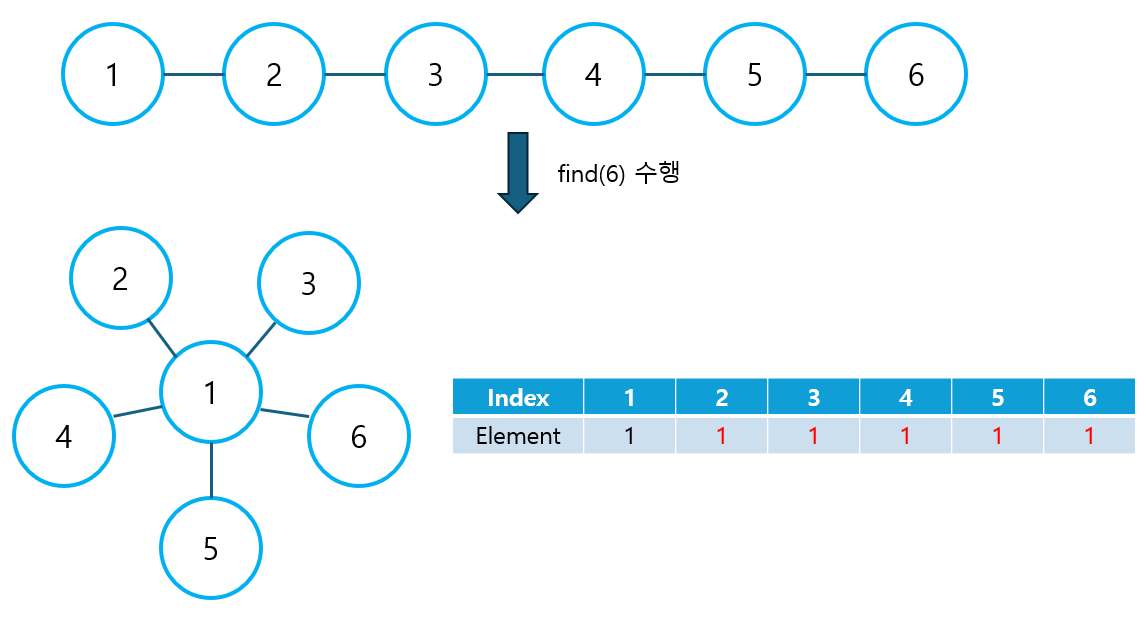
find(6) 연산이 수행된 이후부터는 모든 find(n) 연산의 시간복잡도가 O(1)로 줄어드는 것을 확인할 수 있다. 이처럼 Find 연산은 단순히 대표 노드를 반환하는 역할 뿐 아니라 경로 압축, 그래프 정돈으로써의 의미도 갖고 있다.
2. 문제 풀이
1) 집합 표현하기
두 노드의 대표 노드가 동일하면, 두 노드는 같은 집합에 속하게 된다. 즉, 위 문제는 Union과 Find 연산을 구현하여 풀이할 수 있다.
import sys
input = sys.stdin.readline
sys.setrecursionlimit(2 * 10 ** 8)
n, m = map(int, input().split())
lst = [x for x in range(n + 1)]
def find(a):
if a == lst[a]: # 주어진 노드 번호의 Element 값이 Index와 동일한지 확인
return a
else:
lst[a] = find(lst[a]) # 재귀 호출 동안 거쳐 온 모드 노드의 Element를 대표 노드의 번호로 업데이트
return lst[a]
def union(a, b):
a = find(a) # 대표 노드 탐색
b = find(b)
lst[b] = a # 대표 노드 간 연결
def isSameSet(a, b):
a = find(a)
b = find(b)
return a == b # 대표 노드가 동일한지 여부를 반환
for i in range(m):
x, a, b = map(int, input().split())
if x == 0:
union(a, b)
elif x == 1:
if isSameSet(a, b):
print("YES")
else:
print("NO")입력 값의 범위가 넓은 편이기 때문에, 자칫 잘못하면 시간 초과가 발생할 수도 있는 문제이다. 그럼에도 불구하고, Union Find 알고리즘의 경로 압축 효과 덕분에 주어진 시간 제약 내에 문제를 풀 수 있었다.
2) 여행 계획 짜기
위 문제에서 그래프 간 연결을 인접 행렬을 이용해 표현하고 있으므로, 인접 행렬을 이용한 그래프 표현을 사용해야 할 것으로 보인다. 하지만, 그 외의 직접적인 단서는 존재하지 않으므로, 일단은 위 문제를 풀이하는 방법에 대해 생각해보기로 하자.
첫번째로 떠올릴 수 있는 방법은 E-C-B-C-D의 여행 경로에 대해 DFS를 적용하여 아래의 모든 경로가 가능한지 확인하는 것이다.
- E-C 경로가 가능
- C-B 경로가 가능
- B-C 경로가 가능
- C-D 경로가 가능
당연히 위 4개의 경로가 모두 가능하다면, 해당 여행 경로를 가능하다고 평가할 수 있을 것이고, 그 외의 경우는 불가능하다고 평가할 수 있을 것이다.
물론, DFS를 이용한 풀이도 가능할 것으로 보이지만, 우리에게는 더 좋은 방법이 있다. E-C-B-C-D의 여행 경로가 가능하려면 E, C, B, D가 동일한 대표 노드를 가지면(동일한 집합에 속하면) 된다. 이 내용이 이해가 잘 안 될 수도 있으니, 자세히 설명하기로 하겠다.
E-C 경로가 가능한지에 대해서만 먼저 생각해보자. Union Find의 관점에서 E-C 경로가 가능하려면, E와 C가 동일한 대표 노드를 가져야 할 것이다. 이 내용은 Union Find의 원리 부분에서 배운 내용이다. 예를 들어 아래의 그림에서, 5번 노드와 6번 노드의 대표 노드가 동일하므로, 5번-6번은 가능한 경로이다.
이제 C-B 경로를 살펴보자. C-B 경로가 가능하려면, C와 B가 동일한 대표 노드를 가져야 한다. 이 때, C의 대표 노드는 (E-C 경로가 가능하려면) E와 같아야 하므로, 결과적으로 E, C, B의 대표 노드가 모두 동일하다. 이 내용을 전체 경로에 대해 확장해보면, E-C-B-C-D의 여행 경로가 가능하기 위해선 E, C, B, D가 모두 동일한 대표 노드를 가져야한다는 결론에 도달하게 된다.
import sys
input = sys.stdin.readline
N = int(input())
M = int(input())
graph = [[0 for i in range(N + 1)] for j in range(N + 1)]
lst = [x for x in range(N + 1)]
def find(a):
if a == lst[a]:
return a
else:
lst[a] = find(lst[a])
return lst[a]
def union(a, b):
a = find(a)
b = find(b)
lst[b] = a
for i in range(1, N + 1): # 인접 행렬을 이용한 그래프 표현
graph[i] = [0] + list(map(int, input().split()))
for i in range(1, N + 1):
for j in range(1, N + 1):
if graph[i][j] == 1: # 연결된 노드에 대해 union 연산 수행
union(i, j)
plan = list(map(int, input().split()))
index = find(plan[0]) # 첫번째 노드가 속학 집합의 대표 노드
result = True
for city in plan: # 여행 계획에 포함된 도시를 순회
if find(city) != index:
result = False
break
if result:
print('YES')
else:
print('NO')