1. 위상 정렬
1) 개념
위상 정렬은 유향 그래프에서 노드 간의 순서를 결정하기 위해 사용하는 알고리즘이다. 위상 정렬의 주요 특징은 아래와 같다.
- 그래프 내에 사이클이 존재하지 않아야 한다.
- 정렬 가능한 경우의 수가 유일하지 않을 수 있다.
- 인접 리스트를 이용하여 구현하는 것이 일반적이며, 이 때의 시간 복잡도는 O(V + E)가 된다.
2) 원리
위상 정렬의 원리를 이해하려면 먼저, 진입 차수의 개념을 알아야 하는데, 여기서 진입 차수는 자기 자신을 가리키는 간선의 개수를 의미한다. 자세한 내용은 아래의 예시를 통해 설명하기로 한다.
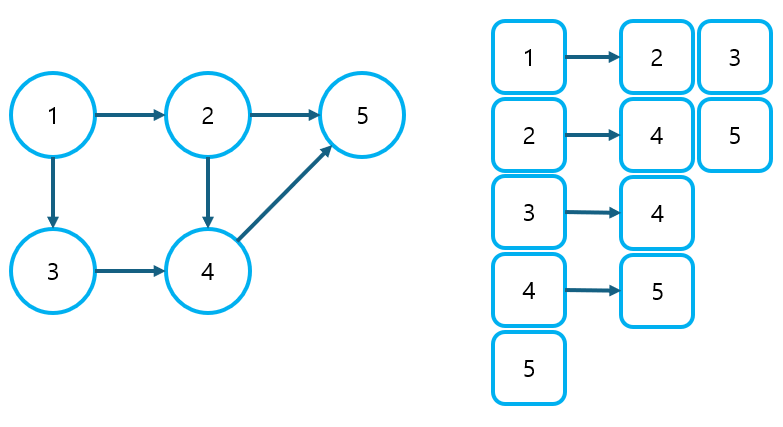
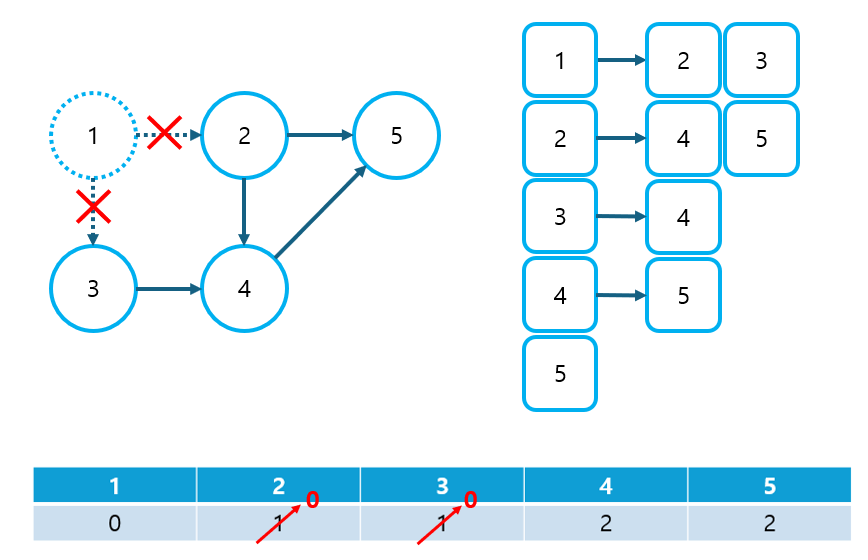
① 인접 리스트를 차례로 순회하며, 진입 차수 리스트 D[N]에 알맞은 값을 알아낸다.
- 1번 노드 순회: D[2]++, D[3]++
- 2번 노드 순회: D[4]++, D[5]++
- 3번 노드 순회: D[4]++
- 4번 노드 순회: D[5]++
② 이렇게 하여 완성된 진입 차수 리스트는 아래와 같을 것이다.

③ 진입 차수가 0인 노드는 시작점을 의미하므로, 가장 먼저 정렬 리스트에 삽입한다.
- 이 때, 진입 차수가 0인 노드가 여러 개인 경우, 순서에 상관 없이 전부 삽입한다. (정렬 가능한 경우의 수가 유일하지 않을 수 있다.)

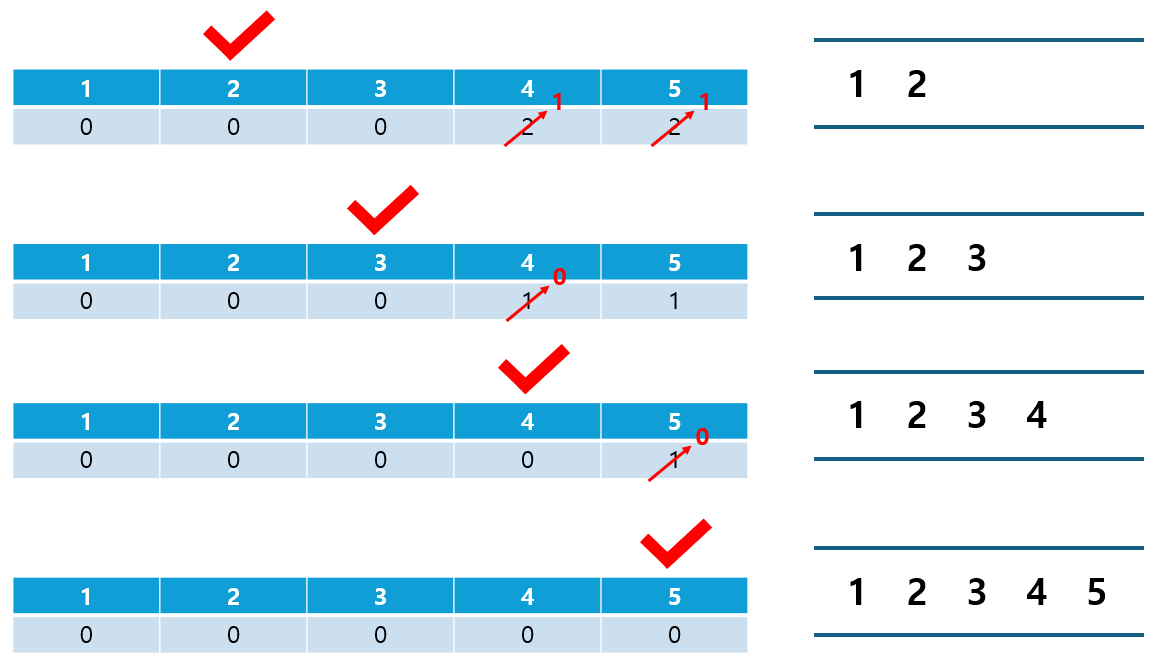
④ 삽입된 노드가 가리키고 있던 노드들의 진입 차수에서 1을 뺀다. 이는 이미 정렬된 노드를 그래프에서 제거한다는 의미이다.
⑤ 변경된 그래프에서 다시 진입 차수가 0인 노드를 찾아 위 과정을 반복한다. 이 과정은 모든 노드가 정렬 리스트에 삽입될 때까지 반복된다.
2. 문제 풀이
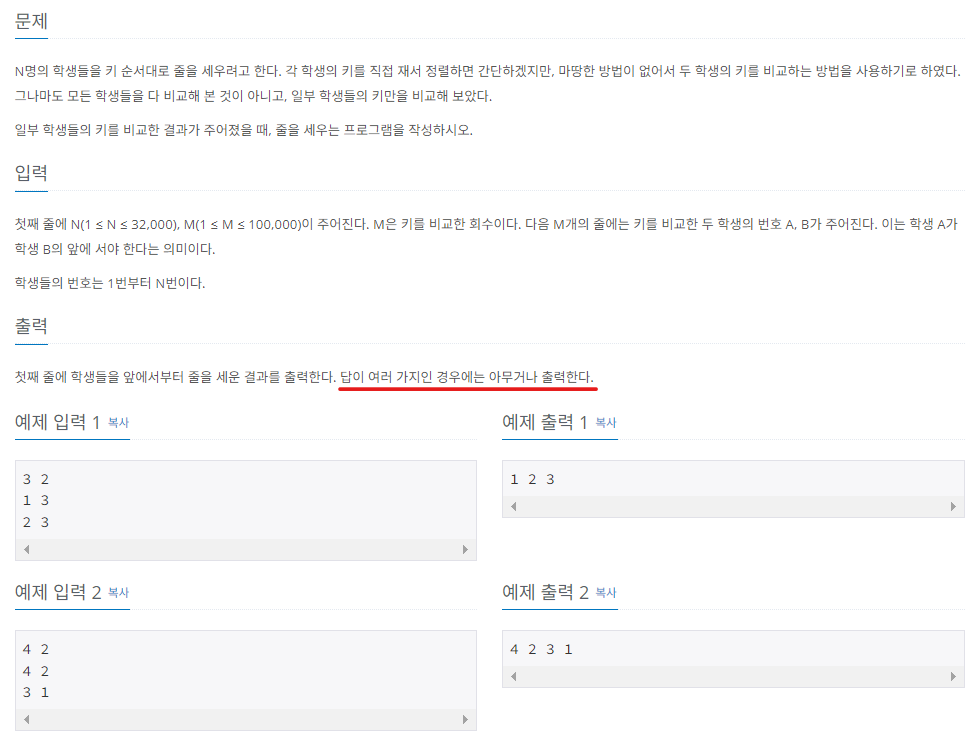
1) 줄 세우기
위상 정렬을 활용해야 하는 대부분의 문제에는 아래와 같은 명확한 단서가 있다.
- 유향 그래프
- 인접 리스트
- 정렬 결과의 다양성
학생을 노드로 간주할 때, 노드 간 연결에 방향성이 존재하므로(키가 작은 학생 → 키가 큰 학생), 이는 유향 그래프이다. 또한, 인접 리스트 형태로 그래프를 표현하고 있으며, 유일한 정렬 결과를 보장하지 않아도 된다. 따라서 위 문제는 위상 정렬을 활용하여 풀이할 수 있다.
import sys
input = sys.stdin.readline
from collections import deque
N, M = map(int, input().split())
# 노드 번호와 인접 리스트의 인덱스를 맞추기 위해 N + 1을 범위로 사용
graph = [[] for _ in range(N + 1)]
# 진입 차수 리스트
lst = [0] * (N + 1)
for i in range(M):
A, B = map(int, input().split())
graph[A].append(B)
lst[B] += 1
# 진입 차수가 0인 노드를 선택 후 잠시 저장할 데크
deq = deque()
# 진입 차수가 0인 노드 선택
for i in range(1, N + 1):
if lst[i] == 0:
deq.append(i)
# 정렬 리스트
result = []
while deq:
selectedNode = deq.popleft()
result.append(selectedNode)
for i in graph[selectedNode]:
lst[i] -= 1 # selectedNode가 가리키고 있던 노드들의 진입 차수에서 1을 뺌.
if lst[i] == 0:
deq.append(i)
print(' '.join(map(str, result)))한 가지 주의해야 할 것은 진입 차수가 0인 노드를 저장하기 위해, 반드시 FIFO 형식의 Queue를 사용해야 한다는 것이다. 이는 LIFO 형식의 자료구조를 사용할 경우, 더 나중에 진입 차수가 0이 된 노드가 먼저 정렬 리스트에 삽입되는 문제가 발생하기 때문이다.
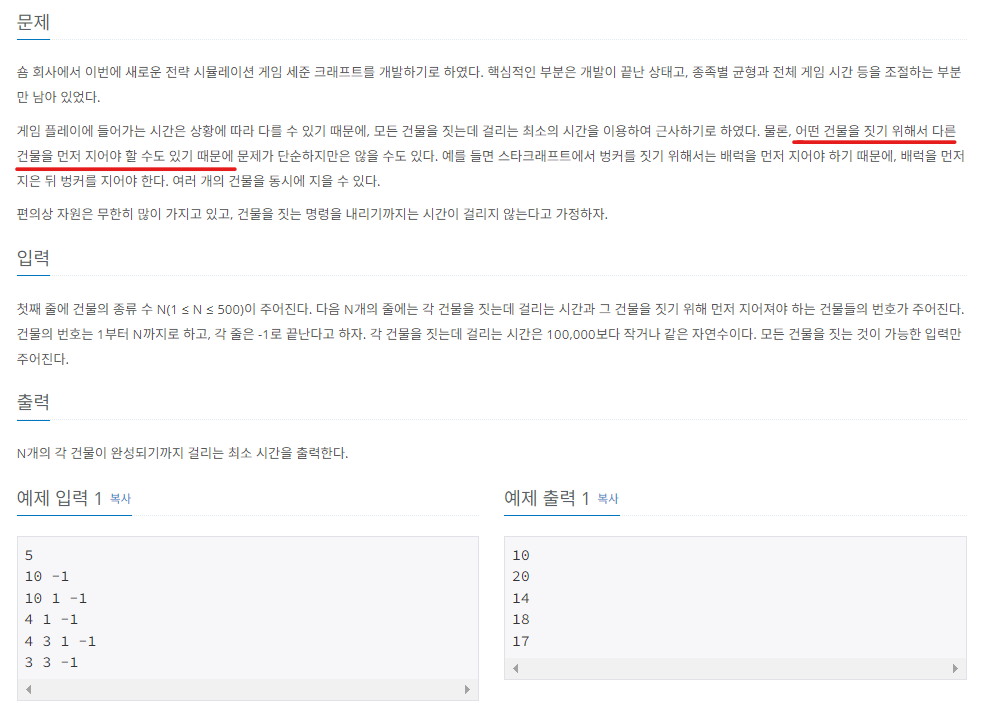
2) 게임 개발하기
위 문제도 위상 정렬을 활용하는 문제임을 쉽게 파악할 수 있을 것이다. (유향 그래프, 인접 리스트, 정렬 결과의 다양성)
import sys
input = sys.stdin.readline
from collections import deque
N = int(input())
# 해당 건물만 짓는 데에 걸리는 순수한 시간, 건물 번호와 인덱스를 맞추기 위해 N + 1 범위까지 생성
time = [0] * (N + 1)
# 인접 리스트
graph = [[] for _ in range(N + 1)]
# 진입 차수 리스트
lst = [0] * (N + 1)
for i in range(1, N + 1):
# 입력 값을 받기 위해 사용하는 임시 배열
temp = list(map(int, input().split()))
time[i] = temp[0]
for j in range(1, len(temp)):
X = temp[j]
if X == -1:
break
else:
graph[X].append(i)
lst[i] += 1
# 진입 차수가 0인 노드를 선택 후 잠시 저장할 데크
deq = deque()
# 진입 차수가 0인 노드 선택
for i in range(1, N + 1):
if lst[i] == 0:
deq.append(i)
# 해당 건물보다 앞서 지어야하는 건물이 지어지기를 기다려야 하는 시간
# 즉, wait와 time을 합쳐 건물이 완성되기 위해 필요한 총 시간을 계산함.
wait = [0] * (N + 1)
while deq:
selectedNode = deq.popleft()
for i in graph[selectedNode]:
wait[i] = max(wait[i], wait[selectedNode] + time[selectedNode]) # 아래 설명 참고
lst[i] -= 1 # selectedNode가 가리키고 있던 노드들의 진입 차수에서 1을 뺌
if lst[i] == 0:
deq.append(i)
for i in range(1, N + 1):
print(wait[i] + time[i])wait[i] = max(wait[i], wait[selectedNode] + time[selectedNode]) 부분이 이해가 잘 안되었을 것 같아 보충 설명을 하도록 하겠다. 이 식은 사실 동적 계획법에서 사용되는 점화식이다. 즉, 건물의 대기 시간을 구하는 복잡한 문제의 해답을, 이전 건물의 대기 시간만을 이용하여 구하고 있는 것이다.
wait 배열에 들어가야 하는 값은 (해당 건물보다 앞서 지어져야 하는 건물의) 대기 시간 + 짓는 시간이다. 이 내용이 wait[selectedNode] + time[selectedNode]에 해당하는 부분이다. 이제 max 함수를 이용하여 기존 wait[i] 값과 비교하는 이유만 이해하면 되는데, 이는 해당 건물보다 앞서 지어져야 하는 건물이 2개 이상인 경우를 고려하기 위함이다.
예를 들어 1번 건물을 짓기 위해 2, 3번 건물이 모두 필요하다고 가정해보자. 2번 건물은 6초가 걸리고, 3번 건물은 10초가 걸린다. (2, 3번 건물보다 앞서 지어져야 하는 건물은 없다고 가정한다.) 이 때, 1번 건물을 짓기 위해 대기해야 하는 시간은 (2번 건물과 3번 건물을 동시에 지을 수 있으므로) 3번 건물이 지어지는 데 필요한 10초이다. 바로 이 과정에서 비교가 발생하는 것이다. 이를 그래프 형태로 설명하면 아래와 같다.
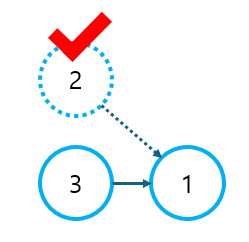
진입 차수가 0인 2, 3번 노드 중 먼저 2번 노드를 Deque에서 popleft() 한다. 초기 상태에서 wait[1] = 0이므로, wait[1] = max(wait[1], wait[2] + time[2]) = wait[2] + time[2] = 0 + 6 = 6이 된다. 다음으로 3번 노드가 Deque에서 popleft() 될 것이다.
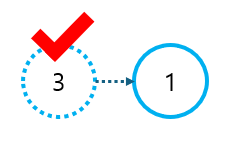
이 때, wait[1] = max(wait[1], wait[3] + time[3]) = max(6, 0 + 10) = 10으로 업데이트가 일어나게 된다. 이로써, 건물을 짓기 위해 대기해야 하는 시간을 계산할 수 있게 된다.
아직 이러한 로직은 좀 어렵게 느껴질 수 있다. 하지만, 나중에 동적 계획법을 학습한 이후부터는 이러한 로직도 자유자재로 이용할 수 있게 될 것이니 걱정하지 않아도 된다.