Graph - 다익스트라

1. 다익스트라

1) 개념

다익스트라는 특정 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 알고리즘이다. 다익스트라의 특징은 아래와 같다.

• 모든 간선의 가중치는 0보다 크거나 같아야 한다.
• 간선과 노드의 수를 각각 E와 V라 할 때, 시간 복잡도는 O(ElogV)가 된다.
• 사이클을 포함하는 그래프에서도 사용 가능하다.
• 유향 그래프와 무향 그래프, 모두에서 사용 가능하다.

사이클이 포함된 그래프에서도 다익스트라가 동작하는 이유는 가중치가 항상 0보다 크거나 같기 때문이다. 바로 이 조건 때문에 이미 방문한 노드로 다시 돌아가는 방법은 결코 최단 경로가 될 수 없다.

2) 원리

다익스트라 알고리즘은 아래의 5단계로 구성된다.

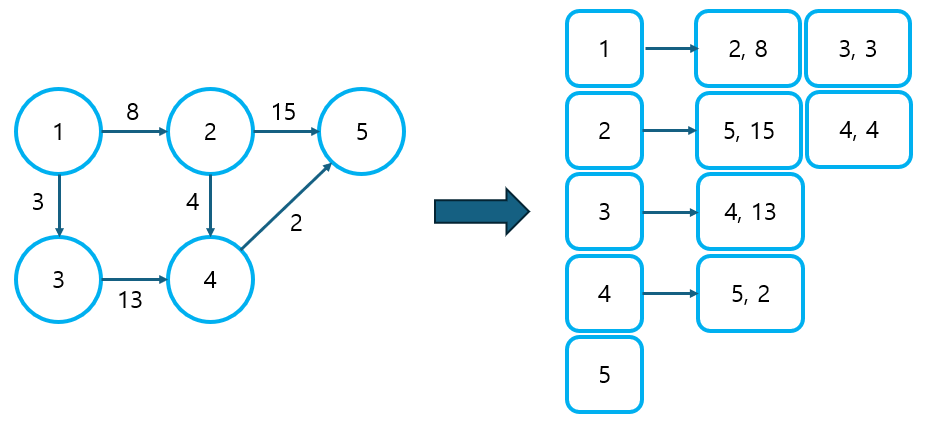
① 인접 리스트를 이용해 그래프를 표현한다.

• 인접 행렬을 이용한 그래프 표현도 가능은 하나, 노드 수가 많아지면 시간 초과가 발생할 수 있으므로, 인접 리스트를 이용해 풀이할 것을 권장한다.
• 인접 리스트에서 노드 번호와 가중치를 한번에 저장하기 위해 튜플이나 배열을 사용할 수 있다.
  

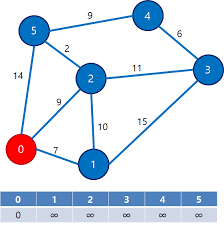
② 최단 거리 리스트를 초기화한다.

• 출발 노드로부터 다른 노드까지의 거리를 저장할 리스트를 생성한다.
• 이 때, 자기 자신까지의 거리는 0으로, 다른 모든 노드로의 거리는 ∞으로 초기화한다. (여기서 ∞은 적당히 큰 수를 의미한다.)
• 여기서는 1번 노드를 출발 노드로 가정한다.

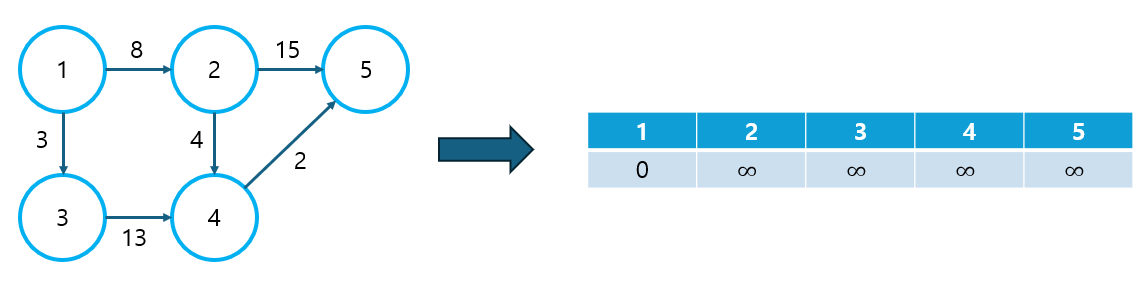
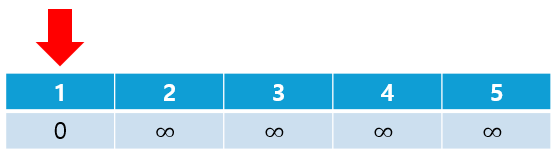
③ 최단 거리 리스트에서 가장 작은 값을 선택한다.

• 아직 방문하지 않은 노드만 선택해야 하기 때문에 방문 여부를 저장하는 visited 배열이 필요하다.
• 처음에는 출발 노드를 선택하게 된다.

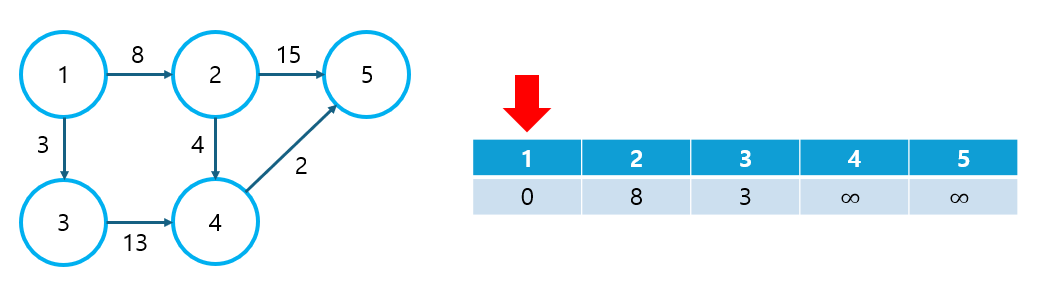
④ 최단 거리 리스트를 업데이트한다.

• 선택된 노드로부터 다른 모든 노드에 이르는 Direct 경로 값으로, 최단 거리 리스트를 업데이트한다.
• Direct 경로가 존재하지 않을 경우, 그대로 ∞으로 표기한다.

⑤ 모든 노드에 방문할 때까지 위 과정을 반복한다.

• 최단 거리 리스트에서 방문하지 않은 노드 중 값이 가장 작은 노드(S)를 선택한다.
• 출발 노드를 A, 도착 노드를 B, 최단 거리 리스트를 D라 하자. 현재 D[B]는 A → B의 Direct 경로 값이 들어가 있다. 이 때, A → B와 A → S → B 중 더 작은 값으로 D[B]를 업데이트 한다.
• 모든 노드를 방문할 때까지, 업데이트를 반복하여 최종적으로 모든 다른 노드로의 최단 경로를 알아낸다.
  

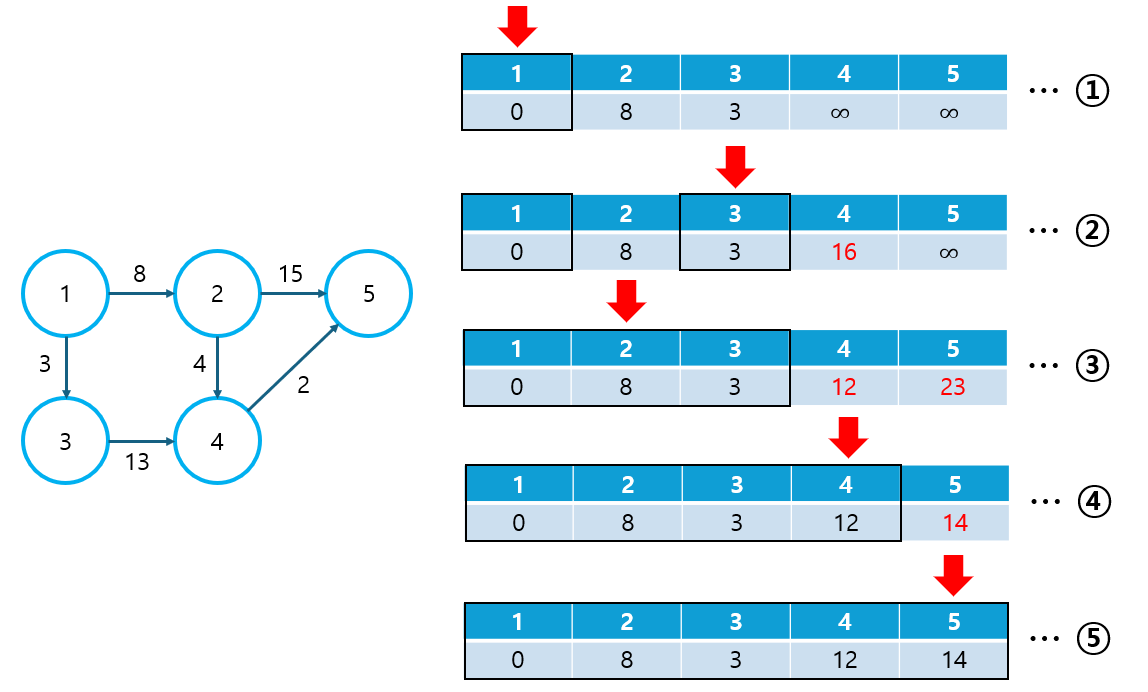
위 그림에서 검은 테두리 사각형은 방문한 노드를 의미한다. 신기한 것은 노드를 방문한 시점에 해당 노드로의 최단 경로가 바로 결정된다(더 이상 업데이트 되지 않는다)는 것이다. 어떻게 4번, 5번 노드를 방문하기도 전에 2번 노드로의 최단 경로가 결정되는 것일까? 단적으로 말하자면, 이는 최단 거리 리스트에서 가장 작은 값을 선택하기 때문이다. 이 내용에 대해서 제대로 이해하려면, 다익스트라 알고리즘을 Greedy 알고리즘의 관점에서 바라볼 수 있어야 한다.

2. Greedy 알고리즘 관점

1) 탐욕적 경로 탐색

다익스트라 알고리즘의 경로 탐색 방식은 Greedy 알고리즘에 기반을 두고 있다.

① 최단 경로가 확정된 집합을 Set이라 하자.

• 초기에는 출발 노드만 Set에 포함되어 있다.
• Set에 포함할 다음 노드를 결정하기 위해 Set과 연결된 노드 중 가중치가 가장 작은 노드(3번 노드)를 선택한다.
• 당연히 이 때 선택된 노드는 해당 노드를 방문하는 최단 경로가 될 것이다.

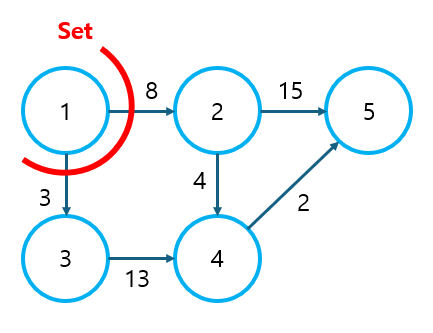
② Set에 포함할 다음 노드를 결정한다.

• Set과 연결된 노드 중 가중치가 가장 작은 노드는 2번 노드이다.
• 이 때, Set에 속하지 않은 노드를 통한 경로는 결코 2번 노드로의 최단 경로가 될 수 없음을 이해해야 한다. (Set은 이미 최단 경로가 확정된 집합이고, Set에서 뻗어 나갈 수 있는 가장 작은 경로를 선택했기 때문)
• 위에 굵게 표시된 내용을 이해했다면, 4번, 5번 노드를 방문하기도 전에 2번 노드로의 최단 경로가 결정될 수 있는 이유도 이해할 수 있을 것이다.
  

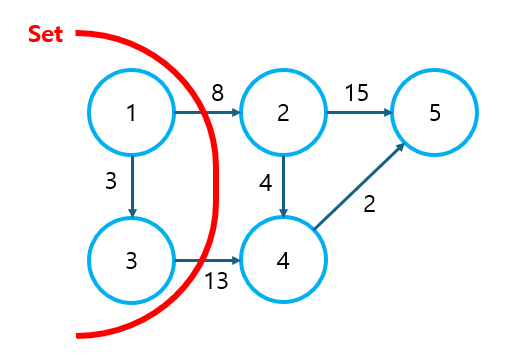
③ 모든 노드가 Set에 포함될 때까지 위 과정을 반복한다.

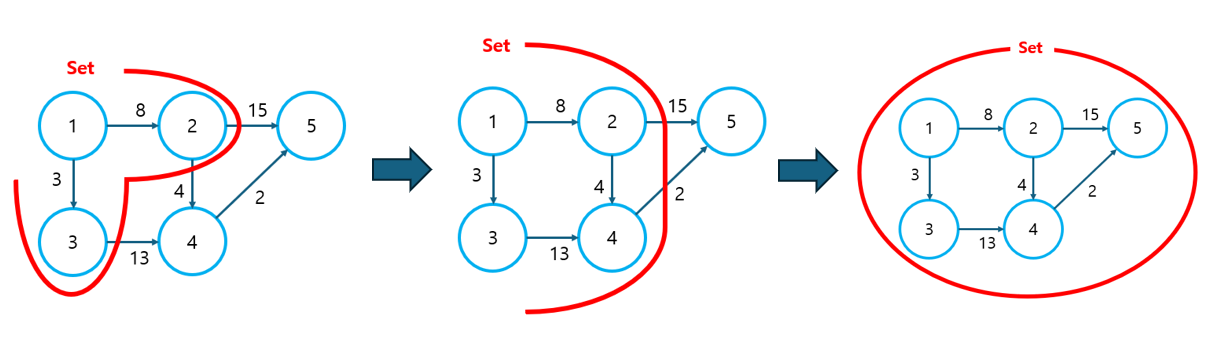
위와 같이 Set에 노드를 포함시키는 과정은 Greedy 알고리즘의 특징을 가지고 있다. 이러한 이유로 Set에 포함된 노드로의 최단 거리는 오직 Set에 포함된 노드만으로 결정될 수 있다. 그리고 이 말을 약간 다르게 표현한 것이 바로 "노드를 방문한 시점에 해당 노드로의 최단 경로가 결정된다"인 것이다.

2) Greedy 알고리즘과의 관계

다익스트라의 원리에 대해 설명할 때, 최단 거리 리스트에서 가장 작은 값을 선택하는 일이 매우 간단한 것처럼 이야기했지만, 사실은 생각보다 쉽지 않다. 그 이유는 최단 거리 리스트가 업데이트 될 때마다, 최소 값이 계속해서 변경되기 때문이다.

하지만, 우리는 이미 해결 방법을 알고 있다. 바로 Greedy 알고리즘과 종종 함께 사용되는 Priority Queue를 이용하는 것이다. 다익스트라 알고리즘에서는 가중치를 우선 순위로 하는 Priority Queue를 사용하여 가중치가 제일 작은(우선 순위가 가장 높은) 값을 찾아낸다. 이로써, 정렬 또는 최소 값 탐색을 위해 필요한 시간을 효율적으로 단축할 수 있게 된다.

참고로, 다익스트라 알고리즘은 Greedy 알고리즘으로 최적해를 보장받을 수 있는, 몇 안 되는 알고리즘이기 때문에, 시간 복잡도가 매우 낮다는 장점이 있다.

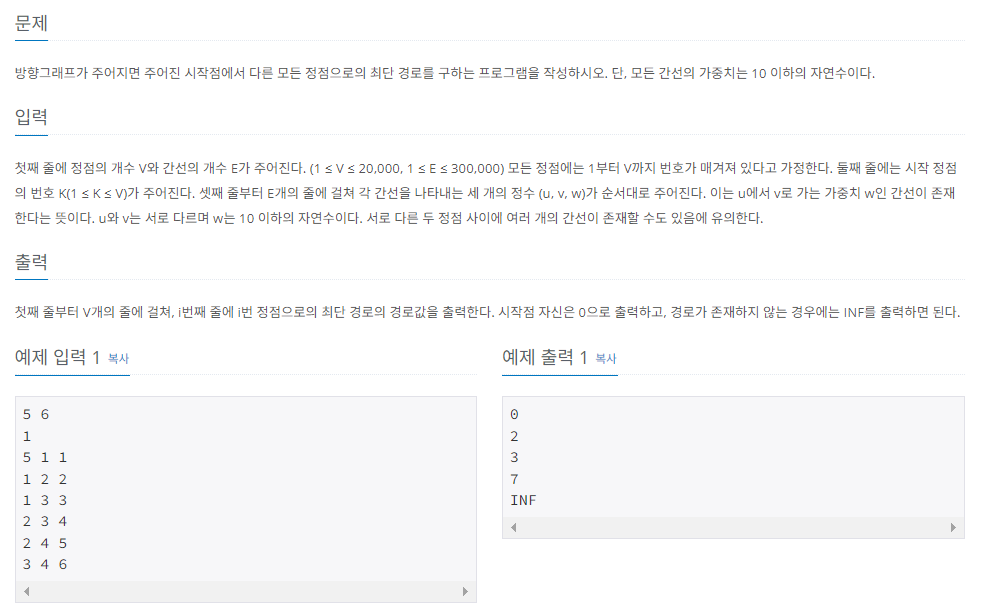
3. 문제 풀이

1) 최단 경로 구하기

>> 백준 1753번

문제 풀이에 앞서 몇가지만 짚고 넘어가기로 하자.

경로가 없다(Infinite)는 말은 어떤 노드가 끊어져 있다는 의미(비연결 그래프)이다. 그렇다면 경로가 없다는 사실은 어떻게 알 수 있을까? 노드를 방문할 때 항상 간선을 따라 이동하므로, visited 배열을 활용하면, 특정 노드의 단절 여부를 효과적으로 판별할 수 있다.

또한 최단 거리 리스트를 초기화할 때, 99999와 같이 적당히 큰 값을 사용하는 것도 방법이지만, sys.maxsize도 매우 큰 수를 빠르게 만들어낼 수 있는 좋은 방법이므로 알아두기로 하자.

import sys
input = sys.stdin.readline
from queue import PriorityQueue

V, E = map(int, input().split())

# 출발 노드
start = int(input())

# 인접 리스트를 이용한 그래프 표현
graph = [[] for _ in range(V + 1)]

for i in range(E):
    u, v, w = map(int, input().split())
    # 튜플 형태로 연결 노드와 가중치를 모두 저장
    graph[u].append((v, w))

# 최단 거리 리스트를 큰 값으로 초기화
dist = [sys.maxsize] * (V + 1) 

# 방문 배열
visited = [0] * (V + 1)

# 자기 자신까지의 거리는 0으로 초기화
dist[start] = 0

def dijkstra(start):
    pq = PriorityQueue() 
    pq.put((0, start)) # 출발 노드의 (가중치, 노드 번호)를 PQ에 삽입

    while pq.qsize() > 0:
        node = pq.get() # 가중치가 가장 작은 튜플(가중치, 노드 번호)을 가져옴. (최단 거리 리스트에서 가장 작은 값을 선택하는 과정에 해당)
        num = node[1] # 노드 번호
        if visited[num] == 0: 
            visited[num] = 1 # 방문 표시
            for temp in graph[num]:
                next = temp[0] # 연결된 노드의 번호
                weight = temp[1] # 가중치
                
                # Direct 경로와 다른 노드를 거쳐가는 경로 중 더 작은 값으로 업데이트
                dist[next] = min(dist[next], dist[num] + weight)
                pq.put((dist[next], next)) # 가중치가 우선 순위의 기준이 됨.
                
        # else 문에 대해서는 아래 설명 참조
        else: 
        	continue

dijkstra(start)

for i in range(1, V + 1):
    if visited[i] == 1:
        print(dist[i])
    else:
        print("INF")

if visited[num] == 0에 대한 else 문은 생략해도 무방하나 이해를 돕기 위해 명시하였다. PQ에 삽입되는 (가중치, 노드 번호) 튜플은 Set에 포함할 다음 노드를 결정하기 위한 것이므로, 아직 해당 튜플의 가중치는 최적 값이 아닐 수 도 있다. (Set에 포함된 이후에 해당 튜플의 가중치가 최적이 된다.) 따라서, PQ에는 최적 값이 아닌 튜플들도 삽입되어 자기 차례를 기다리게 되는데, 이 튜플이 추출될 걱정은 하지 않아도 된다.

그 이유는 PQ에서 get()이 발생하는 시점보다 가중치가 최적의 값을 찾아가는 시점이 더 빠르기 때문이다. 아래의 예시에서 2번 노드가 get() 된 시점에서 이미 4번 노드에 최적의 가중치가 할당된 것을 확인할 수 있다.

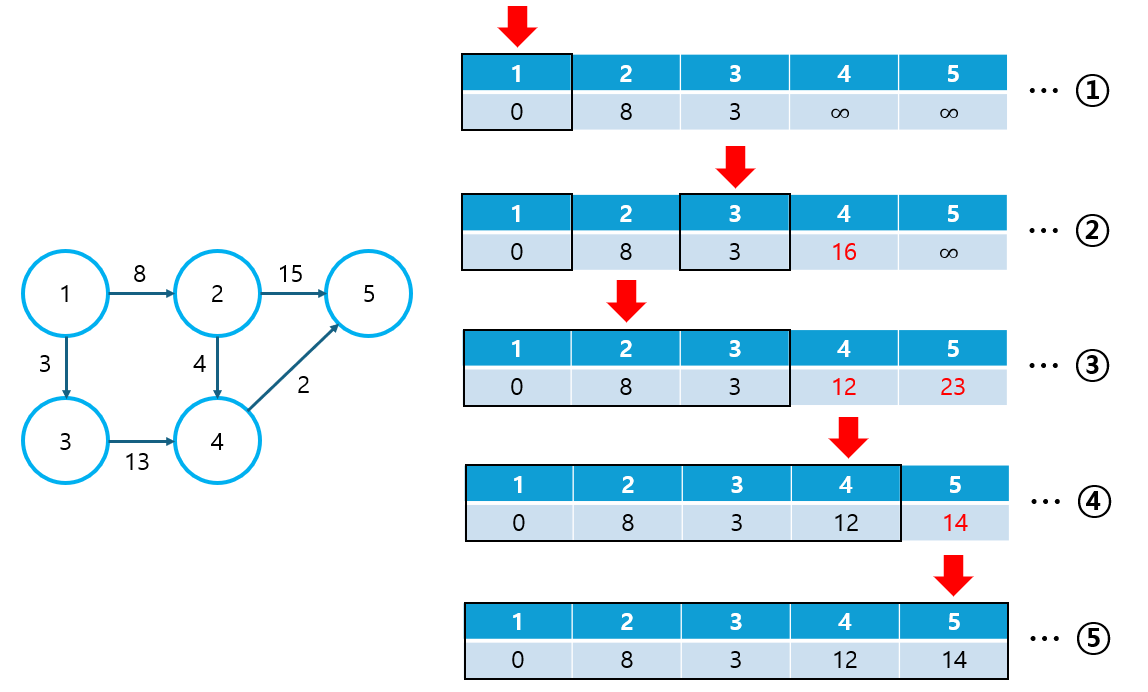
따라서, 최적 값을 가진 튜플이 먼저 get() 되어 visited를 True로 변경하고, 최적 값이 아닌 튜플들은 get() 되자마자 else 문으로 버려지게 되는 것이다.

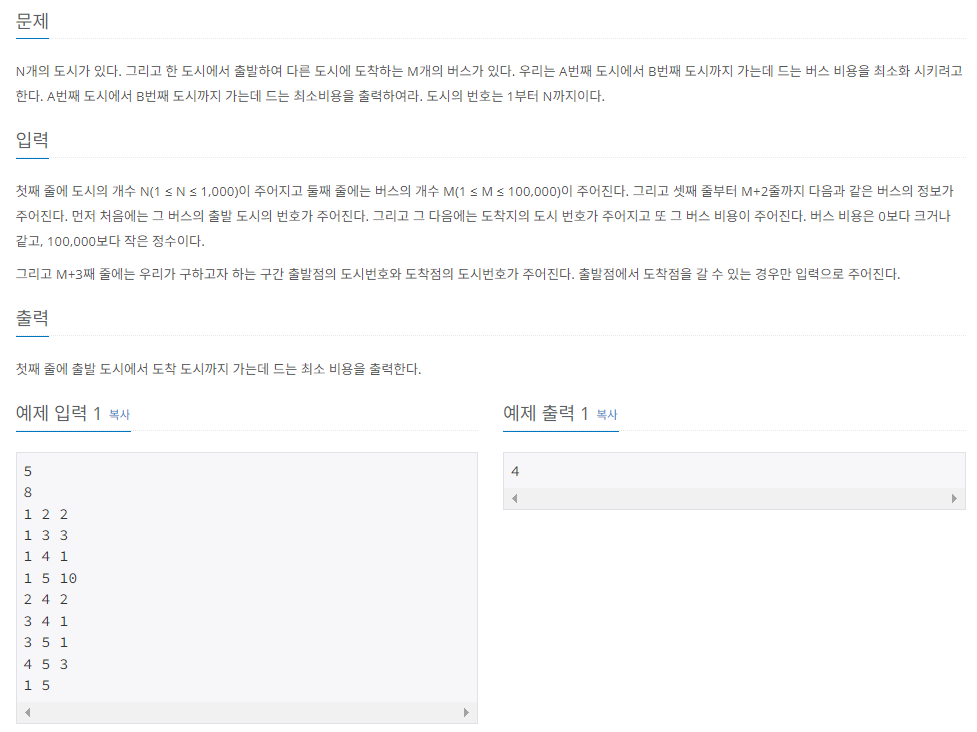
2) 최소 비용 구하기

>> 백준 1916번

위 문제도 다익스트라 알고리즘을 이용하여 동일하게 풀이할 수 있다.

import sys
input = sys.stdin.readline
from queue import PriorityQueue

N = int(input())
M = int(input())

# 인접 리스트를 이용한 그래프 표현
graph = [[] for _ in range(N + 1)]

for i in range(M):
    u, v, w = map(int, input().split())
    graph[u].append((v, w))

start, end = map(int, input().split())

visited = [0] * (N + 1) 

dist = [sys.maxsize]* (N + 1) # 최단 거리 리스트
dist[start] = 0 

def dijkstra(start):
    pq = PriorityQueue()
    pq.put((0, start))

    while pq.qsize() > 0:
        node = pq.get()
        num = node[1] # 노드 번호
        if visited[num] == 0:
            visited[num] = 1

            for temp in graph[num]:
                next = temp[0]
                weight = temp[1]
                dist[next] = min(dist[next], dist[num] + weight)
                pq.put((dist[next], next))

dijkstra(start)
print(dist[end])