Graph - 벨만-포드

1. 벨만-포드

1) 개념

벨만-포드 알고리즘도 다익스트라 알고리즘과 마찬가지로 특정 노드로부터 다른 모든 노드까지의 최단 거리를 구하는 알고리즘이지만, 아래와 같은 차이점이 존재한다.

• 가중치가 음수인 간선이 존재하는 그래프에서도 동작한다.
• 음수 사이클(사이클을 돌았을 때의 결과가 음수)의 존재 여부를 감지하여, 최단 경로가 무한히 작은 값을 갖게 되는 현상을 방지한다.
• 간선과 노드의 수를 각각 E와 V라 할 때, 시간 복잡도는 O(VE)로 다익스트라에 비해 느린 편이다.

참고로, 다익스트라 알고리즘으로 최적해를 구할 수 있는 모든 문제는, 벨만-포드 알고리즘으로도 풀 수 있다. (단, 역은 성립하지 않는다.) 하지만, 벨만-포드 알고리즘은 시간 복잡도가 높기 때문에, 가중치가 음수인 간선이 존재하거나 사이클을 감지해야 하는 상황에서만 사용해야 한다.

2) 원리

벨만-포드 알고리즘은 아래의 4단계로 구성된다.

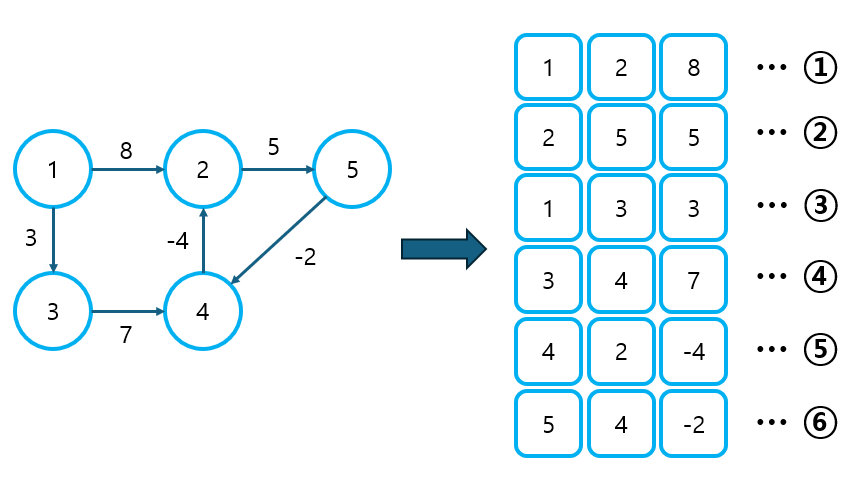
① Edge List를 이용해 그래프를 표현한다.

• 벨만-포드 알고리즘은 간선을 중심으로 동작하므로, Edge List를 이용해 그래프를 표현한다.
• 간선의 [출발, 도착, 가중치] 정보를 한번에 저장하기 위해 튜플 또는 배열을 사용할 수 있다.
  

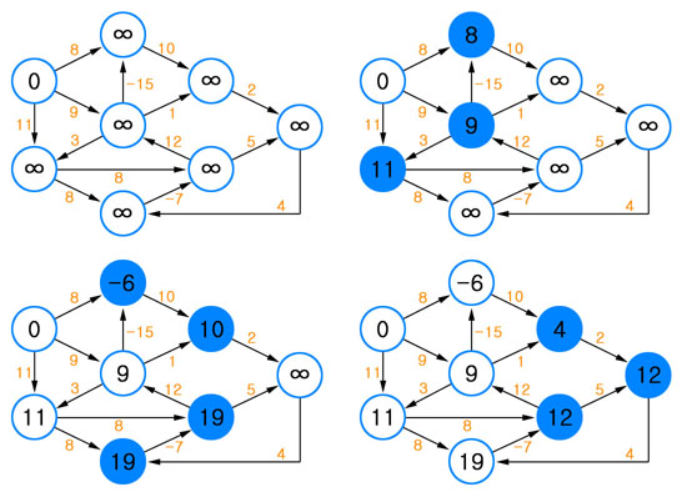
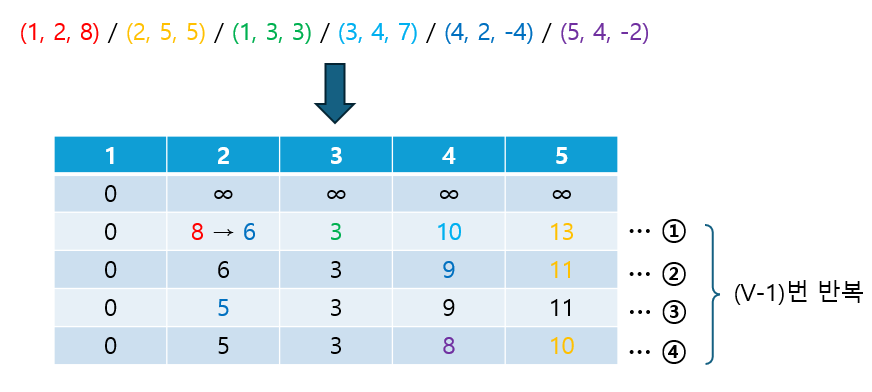
② 최단 거리 리스트를 초기화한다.

• 출발 노드의 값은 0으로, 나머지 노드의 값은 ∞으로 초기화한다.

③ Edge List 순회를 (V-1)번 반복하며, 최단 거리 리스트를 업데이트한다.

• 벨만-포드 알고리즘에서는 매 반복마다 모든 간선을 확인한다. (시간복잡도가 O(VE)인 이유)
• 음수 사이클이 없다고 가정할 때, 특정 두 노드의 최단 거리를 구성하기 위해 필요한 간선의 수는 V-1을 넘을 수 없다. (최악의 경우로 V개의 노드를 모두 거쳐가더라도 V-1개의 간선만 거쳐가기 때문.) 따라서, (V-1)번의 반복 연산으로 최단 거리를 결정할 수 있다.
• edge는 (u, v, w), 최단 거리 리스트는 D라고 할 때, 최단 거리 리스트를 업데이트하기 위한 조건은 아래와 같다.
  • u까지 갈 수 있는 경로가 존재하면서, D[v]의 기존 값보다 u를 거쳐 v로 가는 경로가 더 짧을 경우
  • 조건식: D[u] != ∞ and D[v] > D[u] + w

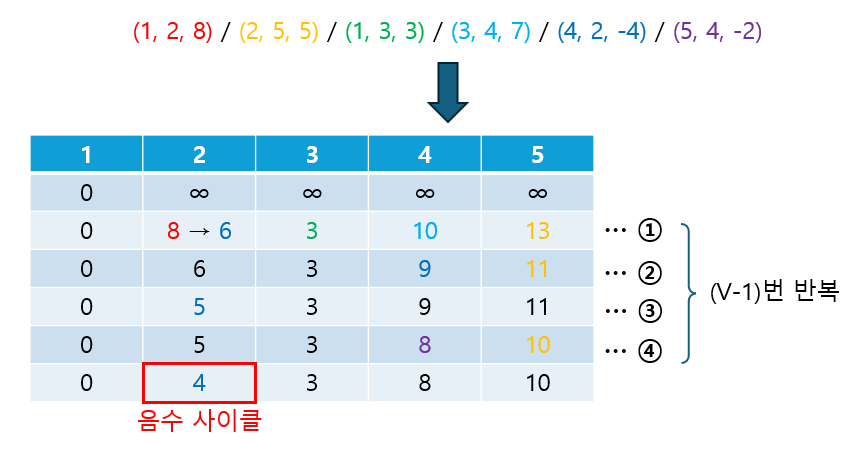
④ 음수 사이클의 존재 여부를 확인한다.

• ③번에서 음수 사이클이 없을 때에는, V-1번의 반복 연산으로 최단 거리를 결정할 수 있다고 배웠다.
• 따라서, V번의 반복 이후에도 최단 거리 리스트가 업데이트 될 경우, 이는 음수 사이클이 존재한다는 의미가 된다.

3) 한번의 추가 반복만으로 음수 사이클을 감지할 수 있는 이유

한번의 추가 반복만으로 음수 사이클을 확실히 감지할 수 있을까? 결론부터 말하면, 음수 사이클은 한번의 반복만으로 반드시 감지된다. 그 이유가 무엇일까?

아래의 그림처럼 V개의 노드에 V개의 간선을 연결한 경로는 반드시 사이클을 형성하게 된다.

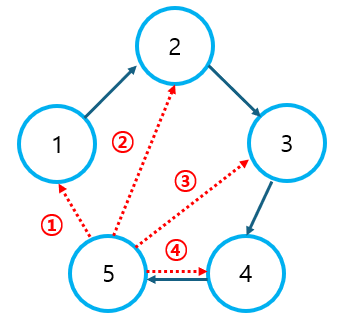
이 때, V개의 간선으로 음수 사이클을 만들 수 없다면, 어떠한 사이클도 최단 경로에 영향을 줄 수 없다. 하지만 반대로, V개의 간선으로 음수 사이클을 만들 수 있다면, 벨만-포드 알고리즘은 가장 낮은 결과를 만들어내는 음수 사이클을 이용하여 최단 거리를 업데이트 할 것이다. 이러한 이유로 벨만-포드 알고리즘은 한 번의 추가 실행만으로, 음수 사이클을 완벽히 감지할 수 있게 된다.

2. 문제 풀이

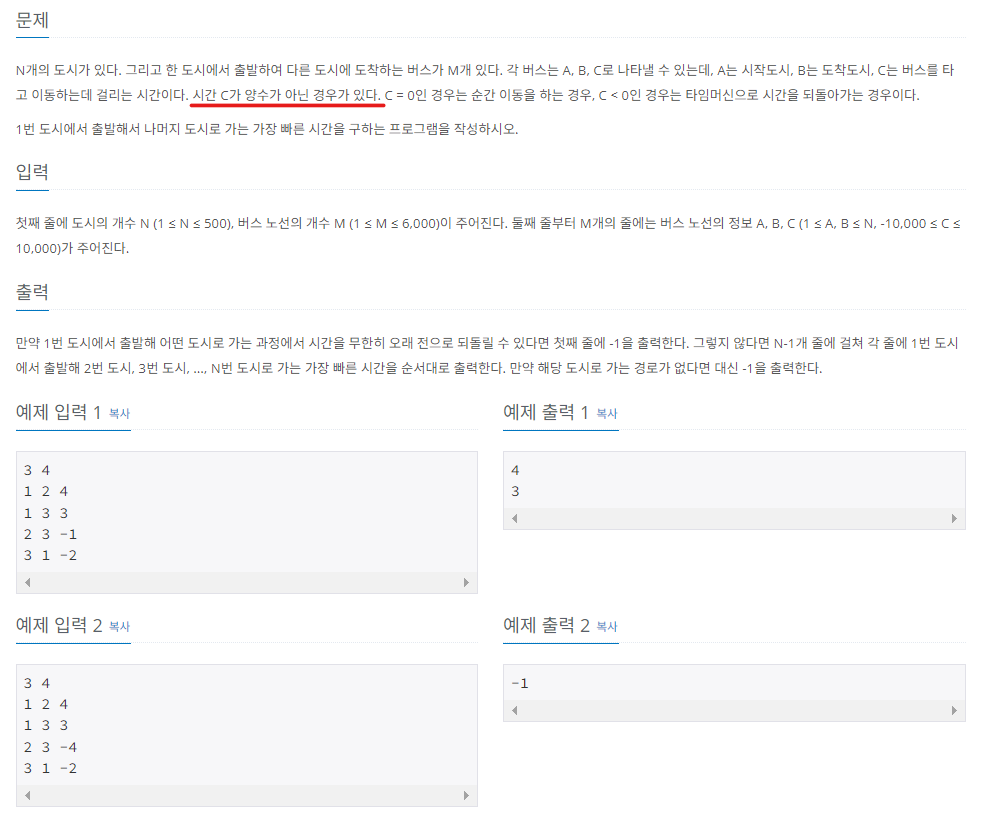
1) 타임머신으로 빨리 가기

>> 백준 11657번

음수 가중치가 포함된 그래프에서의 최단 경로를 구하는 문제이므로, 벨만-포드 알고리즘을 이용해 풀이할 수 있다.

import sys
input = sys.stdin.readline

V, E = map(int, input().split())

edges = [] # edge list

dist = [sys.maxsize] * (V + 1)

for i in range(E):
    u, v, w = map(int, input().split())
    edges.append((u, v, w)) # 튜플 형태로 삽입

dist[1]= 0

for i in range(V - 1):
    for u, v, w in edges:
        if dist[u] != sys.maxsize and dist[v] > dist[u] + w: # 업데이트 조건식
            dist[v] = dist[u] + w
    
isCycle = False # 음수 사이클 확인

for u, v, w in edges:
    if dist[u] != sys.maxsize and dist[v] > dist[u] + w:
        isCycle = True

if isCycle: # 음수 사이클 존재
    print(-1)

else:
    for i in range(2, V + 1):
        if dist[i] != sys.maxsize: 
            print(dist[i])
        else: # 특정 도시로 가는 경로가 없는 경우
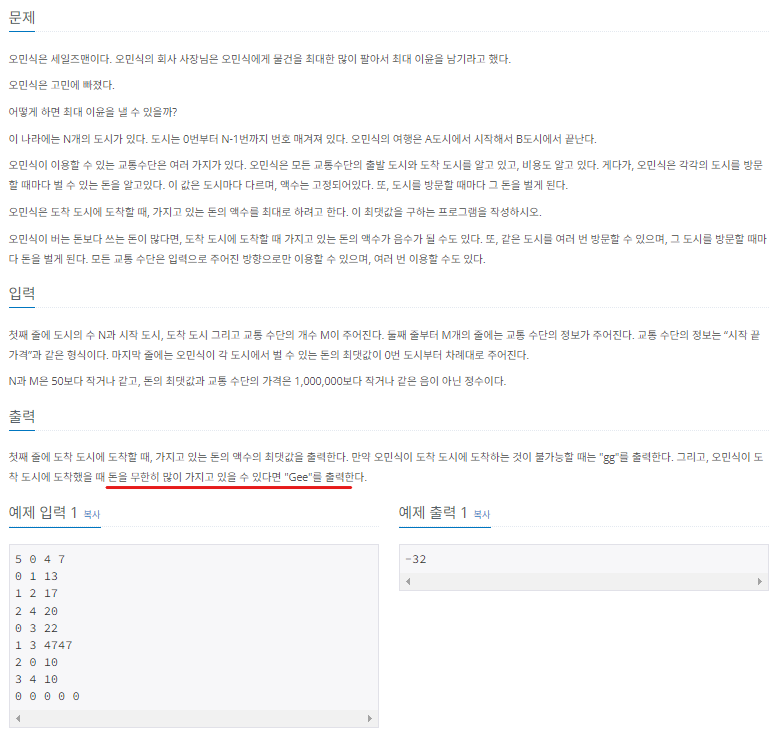
            print(-1)

2) 세일즈맨의 고민

>> 백준 1219번

아래와 같은 단서 중 하나 이상이 주어지면, 이 문제는 벨만-포드 알고리즘으로 풀이될 수 있다.

• 음수 가중치를 갖는 간선
• 사이클 존재 여부 감지

여기서 이야기하고 싶은 내용은, 벨만-포드 알고리즘이 꼭 음수 가중치 간선을 갖는 그래프에서의 최단 거리를 구하는 용도로만 사용되는 것은 아니라는 것이다. 오히려 벨만-포드 알고리즘은 그래프 내의 사이클을 감지하기 위한 용도로 더 자주 사용된다.

다익스트라 알고리즘은 사이클이 존재하는 그래프에서도 동작은 하지만, 사이클을 감지하는 것은 불가능하다. 즉, 간선의 가중치가 항상 양수일 때에도 사이클 존재 여부를 판단해야 한다면, 벨만-포드 알고리즘으로 접근해야 한다는 것이다.

위 문제는 일반적인 벨만-포드 알고리즘의 로직과 약간 상이하지만, 사이클을 감지해야 한다는 단서를 통해 벨만-포드 알고리즘을 사용하는 문제일 것이라 유추할 수 있다. 다만, 아래와 같은 방식으로 알고리즘의 내부 로직을 변경해야 할 것이다.

• 돈의 액수를 최대로 만들기 위해 더 낮은 값이 아닌, 더 높은 값으로 업데이트 해야 한다.
• 돈을 무한히 많이 벌 수 있는 경우를 판별하기 위해 음수 사이클이 아닌 양수 사이클을 찾을 수 있어야 한다.

단, 한가지 주의해야 할 상황이 있는데, 이 상황이 어떤 상황일지는 직접 고민해보기 바란다. 힌트를 주자면, 오민식이 도착 도시에 도착하는 것이 불가능할 때는 gg를, 도착 도시에 도착했을 때 돈을 무한히 가질 수 있다면 Gee를 출력한다 부분을 주의 깊게 살펴보기 바란다. (이 상황이 무엇인지는 코드 아래에 적어놓기로 하겠다.) 이제 문제를 풀어보자.

import sys
input = sys.stdin.readline

N, start, end, M = map(int, input().split())

income = [-sys.maxsize] * N # 더 큰 값으로 업데이트 하기 위해 음의 무한대로 초기화
edges = []

for i in range(M):
    u, v, w = map(int, input().split())
    edges.append((u, v, w))

gain = list(map(int, input().split()))

income[start] = gain[start] # 출발 도시에서 벌 수 있는 돈으로 초기화

for i in range(N + 50): # 아래 설명 참고
    for u, v, w in edges:
        if income[u] == sys.maxsize: # 출발 도시에서 무한히 많은 수익을 얻을 수 있으면
            income[v] = sys.maxsize # 도착 도시에서도 무한히 많은 수익을 얻을 수 있음.

        elif income[u] != -sys.maxsize and income[v] < income[u] + gain[v] - w: # 기존 v에서의 수입보다 u를 거쳐 v로 가는 수익이 더 클 때 
            income[v] = income[u] + gain[v] - w 
            if i > (N - 1): # (N - 1)번의 루프 후에도 업데이트가 발생한다면, 이는 사이클을 돌아 v에 도달했다는 의미가 됨.
                income[v] = sys.maxsize # 즉, v에서 무한히 많은 수익을 얻을 수 있음.
        

if income[end] == -sys.maxsize: # 도달 불가
    print("gg")

elif income[end] == sys.maxsize: # 무한히 많은 수익
    print("Gee")

else:
    print(income[end])

위에서 말한 주의해야 하는 상황은, 양수 사이클을 감지했다고 해서 무조건 Gee를 출력해선 안 된다는 것이다. 그 이유는 양수 사이클을 거쳐 돈을 무한히 많이 벌더라도 도착점에 도달할 수 없다면, gg를 출력해야 하기 때문이다. 아래의 그래프를 보자.

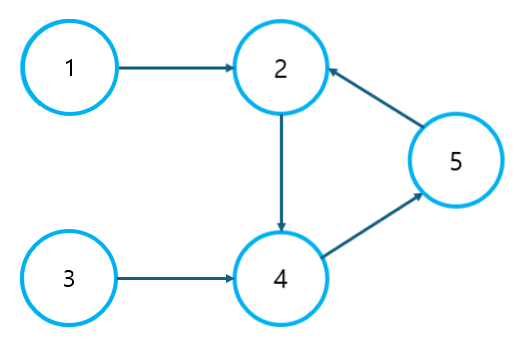
1에서 출발하여 3으로 도착해야 한다고 가정하자. 분명 2-4-5 사이클을 이용해 돈을 무한히 벌 수 있지만, 사이클을 거쳐 도착점에 도달하는 것은 불가능하다. 따라서, 사이클을 감지했다고 해서 무턱대고 Gee를 출력해선 안 되고, 위와 같은 상황을 선별하여 gg를 출력할 수 있어야 한다.

또한, Edge List 순회를 무려 (N + 50)번 수행하는데, 이는 무한히 많은 수익을 얻을 수 있는 노드가 전파되게 하기 위한 것이다. N번째 루프에서 무한히 많은 수익을 얻을 수 있는 노드가 처음으로 발견되는데, 이 노드를 통해서 도달할 수 있는 모든 노드는 무한히 많은 수익을 얻을 수 있는 노드가 된다. 바로 이러한 전파가 충분히 발생할 수 있도록, 노드의 수(또는 간선의 수)만큼의 추가 반복을 진행한 것이다.

개인적으로 깔끔한 문제는 아니라고 생각하지만, 사이클을 감지하기 위해 벨만-포드 알고리즘으로 접근하고, 약간의 내부 로직을 변경하여 풀이하는 방식에서는 배울 점이 많은 문제인 것 같다.