Review 2 - 그래프 표현/Union Find/위상 정렬

Ⅴ. Graph

1. 그래프의 표현

① 그래프 표현

• 문제의 입력이 행렬 형태이거나, 트리 순회를 구현하는 경우가 아니라면, 인접 리스트를 이용하여 그래프를 표현할 것을 권장한다.
• 간선의 방향성이 명확하지 않은 경우, 항상 양방향 간선으로 구현한다.

## N은 노드의 개수, E는 간선의 개수 ##
graph = [[] for i in range(N + 1)]
visited = [0] * (N + 1)

for i in range(E):
	u, v = map(int, input().split())
    arr[u].append(v)
    arr[v].append(u) # 양방향 간선 고려

② 그래프 순회

• 그래프 순회에는 BFS/DFS가 사용되며, 가중치가 없는 그래프에서 노드 간 최단 거리를 찾는 문제는 BFS로 풀이한다.
• DFS를 사용할 때에는, sys.setrecursionlimit을 반드시 붙여주어야 한다.
• 각 노드마다 저장해두어야 할 정보(출발 노드와의 거리, 노드의 색깔 등)가 있는 경우, visited 배열을 최대한 활용한다. 만약, 그 정보가 0도 유효한 값으로 포함하는 경우, visited 배열을 -1로 초기화해야 할 수도 있다.
• 이분 그래프와 같이 비연결 그래프를 허용하는 경우, for 문과 visited 배열을 활용하여 그래프를 순회한다.

for i in range(1, V + 1): # 1번 노드부터 V번 노드까지
	if visited[i] == 0: # 아직 방문하지 않은 노드에 대해
    	bfs(i) # BFS 수행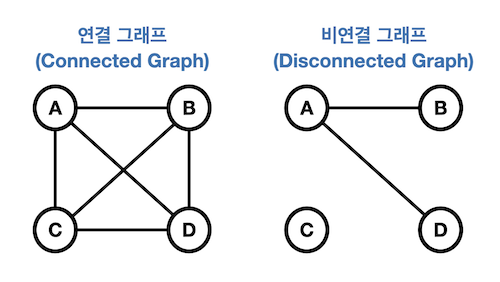

2. Union Find

① 아이디어

• 인덱스를 값으로 갖는 배열을 생성한다.
• 두 노드 간의 Union 연산이 수행되면, 각 노드의 대표 노드끼리 연결되며, 자식 노드의 값은 대표 노드의 값으로 업데이트된다.
• 대표 노드를 찾는 Find 연산의 원리는 아래와 같다.
  • 주어진 노드 번호의 Element 값이 Index와 동일한지 확인한다.
  • 동일하지 않은 경우, Element 값에 해당하는 노드로 이동한다.
  • Element의 값이 Index 값과 동일해질 때까지 위 과정을 반복(재귀 호출)한다.
  • Element의 값이 Index 값과 동일해지면, 이는 대표 노드에 도달했음을 의미하므로, 재귀 함수를 빠져나오면서 거쳐 온 모드 노드의 Element를 대표 노드의 번호로 업데이트한다.

② 코드

lst = [x for x in range(N + 1)] # N은 노드의 개수

def union(a, b):
    a = find(a) # 대표 노드 탐색
    b = find(b)
    lst[b] = a # 대표 노드 간 연결
    
def find(a):
    if a == lst[a]: # 주어진 노드 번호의 Element 값이 Index와 동일한지 확인
        return a
    else:
        lst[a] = find(lst[a]) # 재귀 호출 동안 거쳐 온 모드 노드의 Element를 대표 노드의 번호로 업데이트
        return lst[a] # Element 값에 해당하는 노드로 이동

③ 두 노드 A, B의 대표 노드가 동일하다는 말의 의미

• A, B는 같은 집합에 속해있다.
• A에서 B 또는 B에서 A로 갈 수 있는 경로가 존재한다.

④ 주의 사항

• 노드의 수 N이 1000보다 큰 경우, sys.setrecursionlimit을 반드시 붙여주어야 한다.

3. 위상 정렬

① 특징

• 유향 그래프에서 사용되며, 그래프 내에 사이클이 존재하지 않아야 한다.
• 정렬 가능한 경우의 수가 유일하지 않을 수 있다.
• 인접 리스트를 이용하여 구현된다.

② 구현에 사용되는 자료구조

• 각 노드의 진입 차수를 저장하는 진입 차수 리스트
• 그래프 표현을 위한 인접 리스트
• 진입 차수가 0이 된 노드를 임시로 저장할 Deque
• 정렬된 결과를 저장하기 위한 정답 리스트

③ 아이디어

• 진입 차수 리스트를 생성하고, 인접 리스트를 업데이트 할 때, 진입 차수 리스트의 값도 업데이트 한다.
• 진입 차수가 0인 노드를 Deque에 삽입한다. (진입 차수가 0인 노드가 여러 개인 경우, 순서에 상관 없이 전부 삽입한다.)
• Deque에서 노드를 popleft()하여 정답 리스트에 삽입한 후, 삽입된 노드가 가리키고 있던 노드들의 진입 차수에서 1을 뺀다.
• 이 때, 진입 차수 값이 0이 되면, 해당 노드를 Deque에 삽입한다.이 과정은 Deque가 빌 때까지 반복된다.

④ 위상 정렬의 단서

• 유향 그래프
• 인접 리스트
• 정렬 결과의 다양성