Review 6 - 조합/동적 계획법/기하

Ⅶ. 조합

① 조합 계산 방법

import math

math.comb(N, K)

② DP 테이블 초기화 및 업데이트

# N을 행으로, K를 열로 하는 테이블을 생성한다.
D = [[0 for col in range(N + 1)] for row in range(N + 1)]

# 테이블 초기화
for i in range(N + 1):
    D[i][0] = 1
    D[i][1] = i
    D[i][i] = 1

# 점화식을 이용하여 테이블 값 업데이트
for i in range(3, N + 1): # N >= 3인 경우에만 업데이트 발생
    for j in range(1, i): # K는 N보다 클 수 없다.
        D[i][j] = D[i-1][j] + D[i-1][j-1]

③ 완전 순열의 DP 테이블

• DP 테이블의 Size를 입력 값으로 설정할 경우, 입력 값이 1일 때 D[2] = 1에서 IndexError가 발생한다.
• 따라서, DP 테이블을 고정 크기로 생성할 것을 권장한다.

D = [0 for _ in range(1000001)] 

D[1] = 0
D[2] = 1

for n in range(3, N + 1):
    D[n] = (n - 1) * (D[n - 2] + D[n - 1])

Ⅷ. 동적 계획법

1) 접근법

① DP 적용 조건

• 최적 부분 구조
• 중복 부분 문제

② 주의 사항

• DP 테이블에 Tabulation을 적용할 때, 초기화 범위 이후부터 for 문을 수행해야 한다.

③ 최적 값의 위치를 알 수 없는 경우

• 반드시 현재 인덱스의 값을 포함하여 DP 테이블을 정의해야 한다.

2) 대표 알고리즘

① 카데인 알고리즘

• 주어진 배열에서 부분 합의 최대 값을 찾는 알고리즘이다.
• 최대 부분 합은 아래의 두 가지 경우 중 더 큰 값으로 결정된다.
  • 현재의 원소에서 새로운 부분 배열을 시작하는 경우
  • 이전 부분 배열에 현재 원소를 추가하는 경우
• 점화식: D1[N] = max(lst[N], D1[N-1] + lst[N])
• 원소 1개를 제거하여 얻을 수 있는 최대 부분 합은 아래의 두 가지 경우 중 더 큰 값으로 결정된다.
  • 이미 어떤 원소가 제거된 상태에서 현재 원소를 추가하는 경우
  • 현재 원소를 제거하는 경우
• 점화식: D2[N] = max(D2[N-1] + lst[N], D1[N-1])

② LCS 알고리즘

• 최장 공통 부분 수열을 찾는 알고리즘이다.
• LCS가 계산되는 방법은 아래의 두 가지 경우로 구분된다.
  • 행과 열의 문자가 같은 경우: D[i][j] = D[i-1][j-1] + 1
  • 행과 열의 문자가 다른 경우: D[i][j] = max(D[i-1][j], D[i][j-1])
• 점화식 적용을 위해 zero-padding을 수행해야 한다. zero-padding으로 인해 문자열과 DP 테이블의 인덱스가 1만큼 차이나는 것에 유의한다.
• LCS의 원소를 알아내는 방법은 아래와 같다.
  • 테이블의 마지막 인덱스에서 시작
  • 행과 열의 문자가 같은 경우, 그 값을 저장한 후 대각선 왼쪽으로 이동
  • 행과 열의 문자가 다른 경우, 왼쪽과 위쪽 중 더 큰 값쪽으로 이동
  • 저장된 값을 역순으로 출력

③ 연쇄 행렬 곱셈

# N은 행렬의 개수
# lst는 행렬의 행과 열을 저장하고 있는 배열

D = [[sys.maxsize for i in range(N)] for j in range(N)] # 최소 값을 구할 때는 maxsize로 초기화

for i in range(N): # D[i][j]에서 i == j이면, 행렬이 하나라는 의미이므로 필요한 연산의 수는 0이 됨.
    D[i][i] = 0

for cnt in range(2, N + 1): # i와 j 사이의 존재하는 행렬의 개수(i와 j 행렬도 포함)
    for i in range(N - cnt + 1): 
        j = i + cnt - 1

        for k in range(i, j):
            D[i][j] = min(D[i][k] + D[k + 1][j] + lst[i][0] * lst[k][1] * lst[j][1], D[i][j])

print(D[0][N - 1]) # 인덱스가 0부터 시작하므로, 0번 행렬부터 N-1번 행렬까지의 최소 연산 횟수로 구해야 함.

④ TSP 알고리즘

• 점화식
  
• 부분 집합을 비트 마스킹으로 표현
• 시작 정점은 임의로 정의 가능
• Top-Down Approach와 Memoization을 이용하여 풀이

Ⅸ. 기하

① CCW 계산 방법

② CCW의 의미

• CCW > 0: 점 A, B, C가 반시계 방향으로 놓여 있다.
• CCW = 0: 점 A, B, C가 일직선 상의 점이다.
• CCW < 0: 점 A, B, C가 시계 방향으로 놓여 있다.

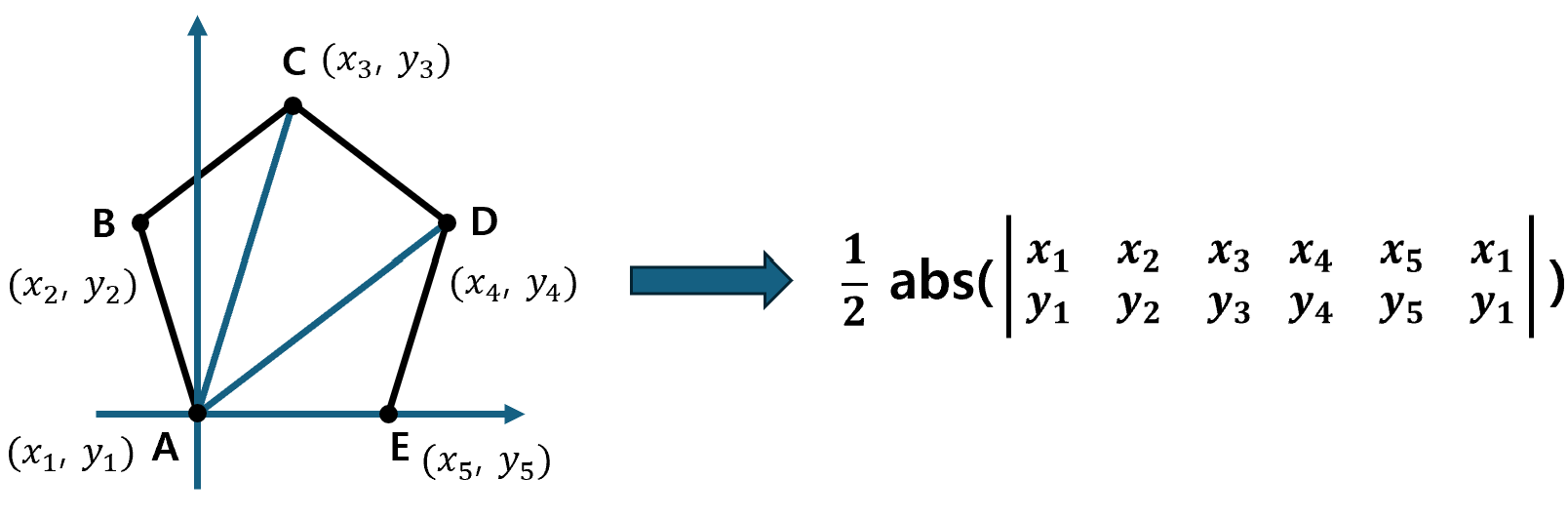
③ 다각형의 넓이

• 삼각형의 넓이를 구하는 공식을, 다각형으로 확장 가능
• 외적 결과에 절대 값을 취하고 1/2을 곱하는 일을, 잊어버리지 않도록 주의
  

④ 코드

def CCW(x1, y1, x2, y2, x3, y3):
    ccw = (x1 * y2 + x2 * y3 + x3 * y1) - (x2 * y1 + x3 * y2 + x1 * y3)

    if ccw > 0 :
        return 1
    elif ccw == 0:
        return 0
    else:
        return -1