1. 개념
그리디 알고리즘은 각 단계에서 최선의 선택을, 최적의 선택지로 가정하는 알고리즘이다. 물론, 각 단계에서 선택된 해가 최적해일 것이라는 보장은 없지만, 구현이 쉽고 시간 복잡도가 낮기 때문에 최적해를 구하는 일부 문제에 유용하게 사용될 수 있다. 그리디 알고리즘은 아래의 3단계를 반복하면서 주어진 문제에 대한 해답을 찾아나간다.
① 해 선택 단계
- 현재 상태에서 가장 최선이라고 생각되는 해를 선택
② 해결 단계
- 선택된 해가 문제의 제약조건에 위배되지 않는지 검사
③ 최적해 검사 단계
- 현재까지 선택된 해집합이 전체 문제에 대한 해결책이 될 수 있는지 검사
- 해결할 수 없다면, 다시 ①단계로 회귀
실생활에서도 그리디 알고리즘이 활용되는 경우가 있는데, 바로 거스름 돈을 줄 때이다. 거스름 돈이 17600원이라고 해보자. 일반적인 경우에 10000원 + 5000원 + 1000원 2장 + 500원 + 100원으로 거슬러줄텐데, 이 방법이 실제로 가장 적은 지폐(동전) 수로 거슬러주는 최적의 방법이다.
거스름 돈을 계산할 때, 그리디 알고리즘으로 최적의 해를 얻을 수 있는 이유는 화폐의 단위가 서로 배수 관계에 있기 때문이다. 이처럼 큰 단위가 작은 단위의 배수일 때에는, 사용 가능한 큰 단위 대신 작은 단위를 조합하는 방식으로는 결코 최적해를 얻을 수 없다. 즉, 모든 원소들이 서로 배수 관계에 놓여있을 때에는 그리디 알고리즘으로 최적해를 보장받을 수 있는 것이다.
만약 화폐 단위가 서로 배수 관계에 있지 않다면 어떨까? 예를 들어, 화폐의 단위가 5000원, 4000원, 1000원이라 할 때 8000원을 거슬러 주어야 하는 상황을 생각해보자. 그리디 알고리즘을 적용하면 5000원 + 1000원 3장 이라는 결과가 나오겠지만, 사실 4000원 2장이 최적의 해이다. 즉, 그리디 알고리즘이 최적해를 보장하지 못하고 있는 것이다.
2. 문제 풀이
그리디 알고리즘의 개념은 간단하므로, 실제 문제 풀이에 바로 적용해보기로 하자.
1) 동전 개수의 최솟값 구하기
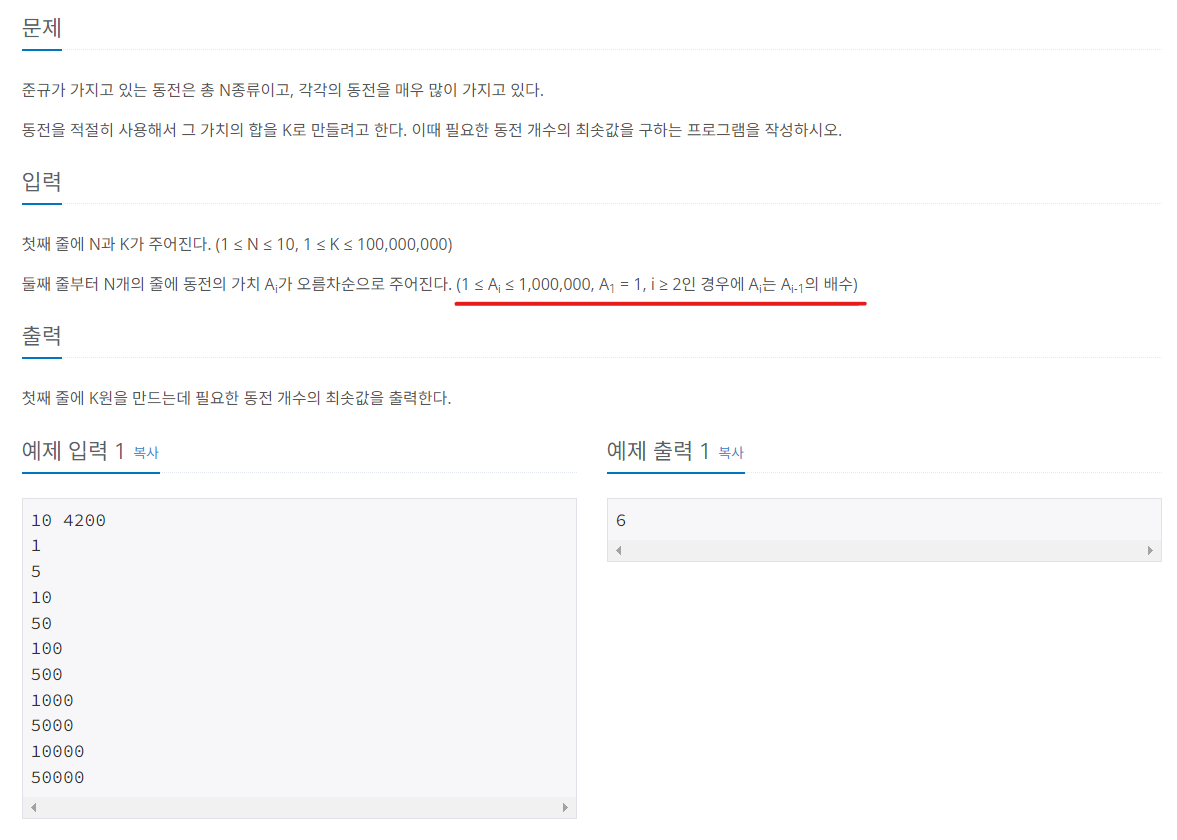
거스름 돈을 계산하는 방식과 동일한 문제이면서, 동전의 단위가 서로 배수 관계에 놓여있다. 우리는 이러한 내용을 통해, 위 문제에 그리디 알고리즘을 적용해야 함을 알아차릴 수 있다.
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
coins = []
for i in range(N):
coins.append(int(input()))
coins.sort(reverse=True) # 큰 값을 우선적으로 선택하기 위해 내림차순 정렬
result = 0
for coin in coins:
if coin <= K:
result += K // coin # 사용 가능한 가장 큰 단위의 동전을 최대한으로 사용
K %= coin # K를 계산 후 남은 돈으로 업데이트
if K == 0: # 남은 돈이 없을 때 반복문 탈출
break
print(result)2) 카드 정렬하기
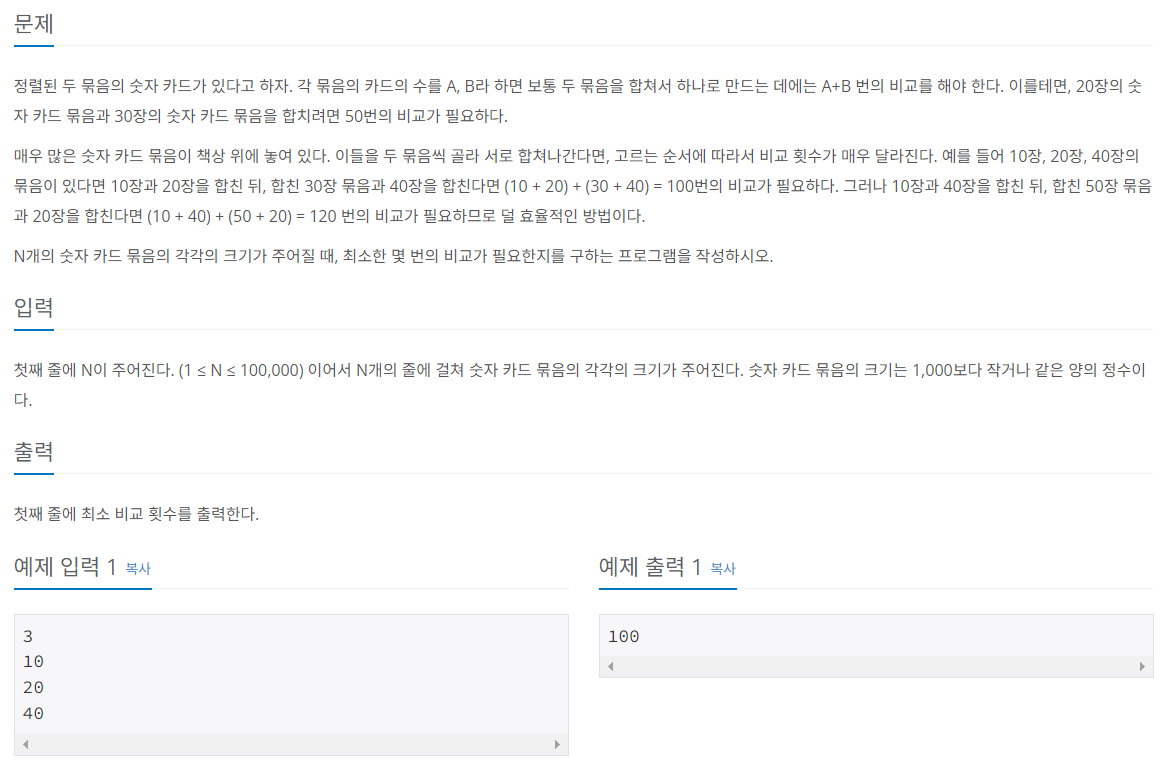
위 문제는 언뜻 보기엔 Deck의 size를 오름차순으로 정렬한 후 앞에서부터 더하는 방식으로 쉽게 풀이될 것 같지만, 그렇지 않다. 위에서 주어진 예시가 Deck이 3개일 때만 주어져서 혼동하기 쉽지만, Deck이 4개 이상일 때부터는 이와 같은 방법을 사용할 수 없다.
예를 들어, Deck의 size가 40, 60, 70, 80으로 주어졌다고 하자. 오름차순 정렬 후 앞에서부터 더하는 방식으로 계산하면, (40 + 60) + (100 + 70) + (170 + 80) = 520번의 비교가 필요할 것이다. 그러나, 40과 60의 Deck을 합치고 70과 80의 Deck을 합친 후에 두 Deck을 합치면, (40 + 60) + (70 + 80) + (100 + 150) = 500번의 비교만 필요하다. 즉, Deck이 합쳐질 때마다 다시 정렬을 수행한 후에 앞에서부터 더해야 한다는 것이다.
그러나, 만약 Deck이 합쳐질 때마다 정렬을 수행한다면, NlogN의 시간복잡도로 N-1번을 반복해야 하는데, 최악의 경우 N=10^5이므로, 정렬만 수행해도 주어진 시간(2초)을 초과해버릴 것이다.
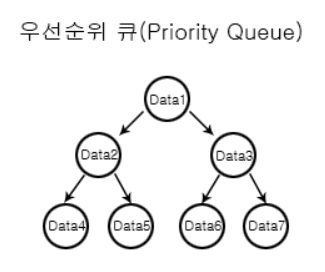
바로 이 과정에서 그리디 알고리즘을 떠올릴 수 있어야 한다. 그리디 알고리즘은 항상 각 상태에서의 최대값(또는 최소값)을 선택한다는 점에서 정렬과 관계가 깊다. 이러한 이유에서 그리디 알고리즘은 종종 Priority Queue와 함께 사용된다.
※ Priority Queue
먼저 들어온 데이터가 먼저 나가는 FIFO 형식의 Queue와는 달리, Priority Queue에선 우선순위가 높은 데이터가 먼저 나간다. 즉, 각 요소에는 우선 순위가 할당되어 있으며, 이 우선순위에 따라 요소들이 정렬되어 있다. 우선 순위 큐는 일반적으로 heap 자료 구조를 사용하여 구현되며, 파이썬에서는 모듈을 import하는 것만으로 간편하게 사용할 수 있다. Priority Queue 모듈을 사용하기 위한 import 구문과 제공되는 메서드의 사용법은 각각 아래와 같다.from queue import PriorityQueue
- put((우선순위, 아이템)), put(숫자): 우선순위는 숫자로 표현되어야 하며, 작은 숫자일수록 우선권을 갖는다. 숫자를 바로 put 할 경우, 해당 숫자는 아이템임과 동시에 우선순위가 되며, 우선 순위와 별도로 아이템을 지정하고 싶다면 튜플의 형태로 put 해야 한다.
- get(): 큐에서 우선순위가 가장 높은 아이템을 반환하고, 해당 아이템을 큐에서 제거한다.
- empty(): 큐가 비어 있는지 여부를 True/False로 반환한다. 일반적으로
while not pq.empty()형태로 큐를 순회하기 위한 목적으로 사용된다.- qsize(): 큐에 현재 저장된 아이템의 개수를 반환한다.
이제 Priority Queue를 이용하여 문제를 풀어보자.
import sys
input = sys.stdin.readline
from queue import PriorityQueue
N = int(input())
pq = PriorityQueue()
for i in range(N):
pq.put(int(input()))
sum = 0
while pq.qsize() > 1: # pq에는 항상 최소 한 개의 요소가 남게 되므로, empty()를 써선 안 된다.
data1 = pq.get()
data2 = pq.get()
sum += data1 + data2
pq.put(data1 + data2)
print(sum)