안되면 외우자

안되면 외우자 백준 티어는 전혀 의미없다고 생각하지만, 필자의 수준을 소개하자면...

제일 약한 파트 3가지 백트래킹,dp,그리디에 대해 알아보자!현재 상태에서 가능한 모든 후보군을 따라들어가며 탐색정의는 이렇다. 생각나는대로 일단 정의해보자.재귀를 이용한다. 특히 DFS를 이용한다. => 인접한 방향(노드)부터 탐색해 나간다.DFS를 이용한다

너무나 큰 정의긴한데, 어쨌든 수식을 세워서 풀 수 있는 종류이다.예를들면 최소공배수, 최대공약수, 에라토스테네스의 체(소수 판별 알고리즘), 모듈러 연산 등!따로 내릴 수 있는 정의는 없다.소수란 1과 자기자신으로만 나뉘어지는 수 이다.간단하게 구현하면 아래와 같다.

그래프는 알고리즘은 아니고 자료구조다. 어떤 자료구조일까?정점과 간선으로 이루어진 자료구조 => 정점과 간선이 존재하면 그래프다!차수(degree)는 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수다!방향이나 가중치가 존재할 수 있다!방향그래프에서 나가는 간선은

위상정렬은 들어보기만 했고 아예 모르는 알고리즘이다! 위상정렬은 대체 뭘까?방향 그래프에서 간선으로 주어진 정점 간 선후 관계를 위배하지 않도록 나열하는 정렬.출처아하 그러니까 방향 그래프에서 출발 정점이 도착 정점보다 앞에 오는 정렬이다.쉽게 설명하자면 선수 과목을

최단거리를 구하는 대표적인 알고리즘 두가지중 하나다. 모든 정점 쌍 사이의 최단거리를 구하는 알고리즘이다. 모든 정점 간의 최단거리를 구하기때문에 시간복잡도가 크다. O(V^3) => 보통 n이 1000까지는 가능하다.핵심은 start에서 to로 가는 거리 vs sta

lowerbound & upperbound combination & permutation

combination 전편에서사용한 템플릿이 원래 쓰던 템플릿과 달라서 혼란이 왔다. 그래서 사용하던 템플릿으로 다시 만들어보았다. 1) 조합 조합의 핵심은 현재 선택된 원소를 제외한 나머지 원소를 순차적으로 고르는 것이다. 즉 이번에i번째부터 원소를 골랐다면,

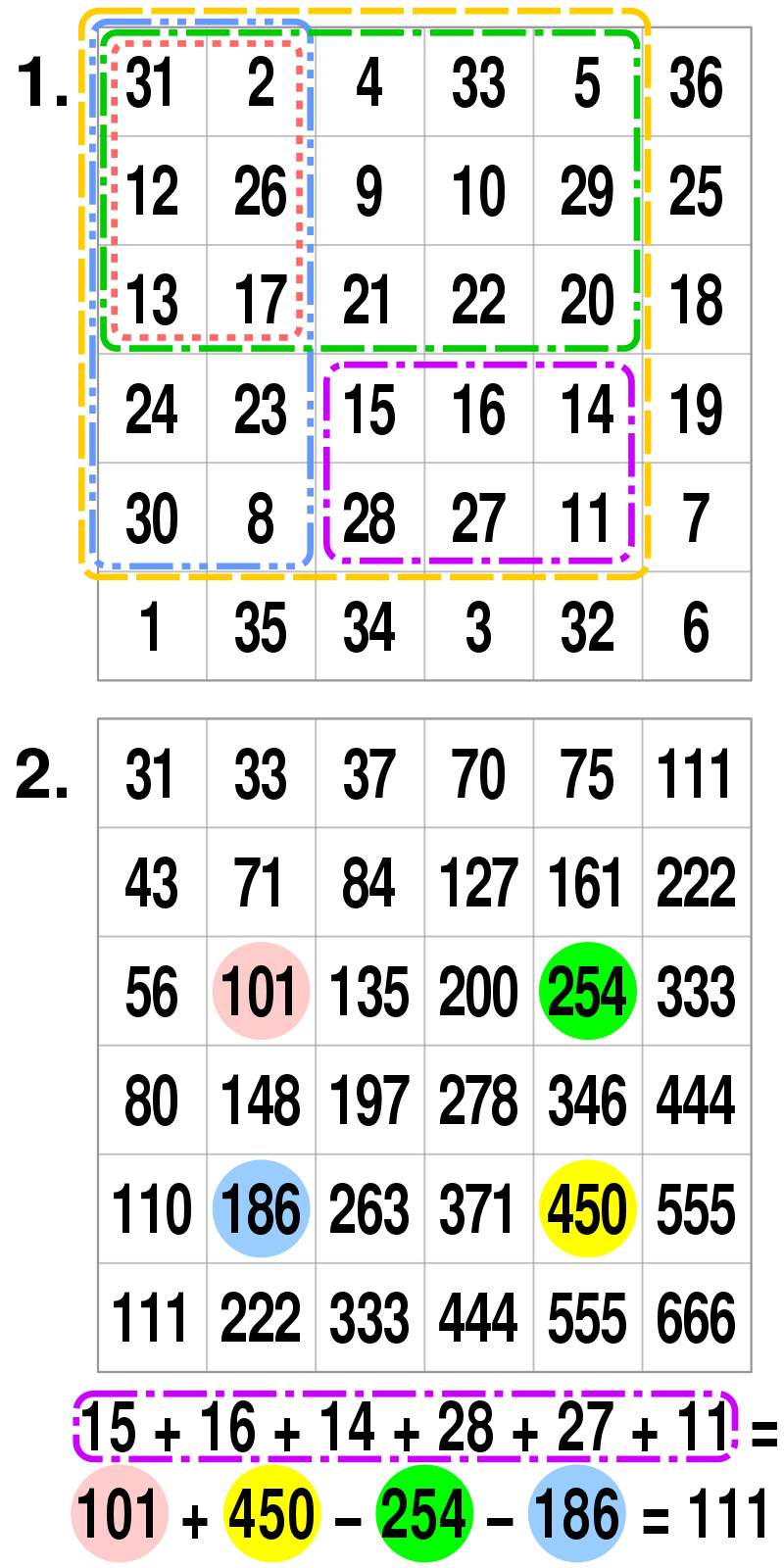
누적합 누적합은 DP라고 볼수있다. 특정 점화식을 구하여 상향식으로 접근한다. 아래와 같은 예시를 보자. 예를들어 길이가 n인배열에서 [a,b]의 구간합을 구해야한다. 나이브하게 작성한다면 다음과 같은 알고리즘이 될 것이다. 위 알고리즘은 간단명료하고 잘 작동한다.