combination

전편에서사용한 템플릿이 원래 쓰던 템플릿과 달라서 혼란이 왔다.
그래서 사용하던 템플릿으로 다시 만들어보았다.

1) 조합

조합의 핵심은 현재 선택된 원소를 제외한 나머지 원소를 순차적으로 고르는 것이다.
즉 이번에i번째부터 원소를 골랐다면, 다음은 i+1, i+2, i+3...번째부터 고르면 된다.

const combination = (k, index, arr, result, temp = []) => {
	if(temp.length === k){
    	result.push([...temp]);
    	return;
    }
    for(let i = index; i<arr.length; i++){
    	temp.push(arr[i]);
        //현재 원소 이후만 관심있기에 index에 i+1를 넣어준다.
    	combination(k, i+1, arr, result, temp); 
      	temp.pop();
    }
}
const result = [];
combination(3,0,[1,2,3,4,5],result);

2) 중복조합

중복 조합은 선택한 원소를 계속고를 수 있다. 즉, i번째 원소를 골랐지만, i번째부터 골라도 된다.

const dupCombination = (k, index, arr, result, temp = []) => {
	if(temp.length === k){
    	result.push([...temp]);
    	return;
    }
    for(let i = index; i<arr.length; i++){
    	temp.push(arr[i]);
        //현재 원소도 관심있기에 i를 넣어준다.
    	dupCombination(k, i, arr, result, temp); 
      	temp.pop();
    }
}
const result = [];
dupCombination(3,0,[1,2,3,4,5],result);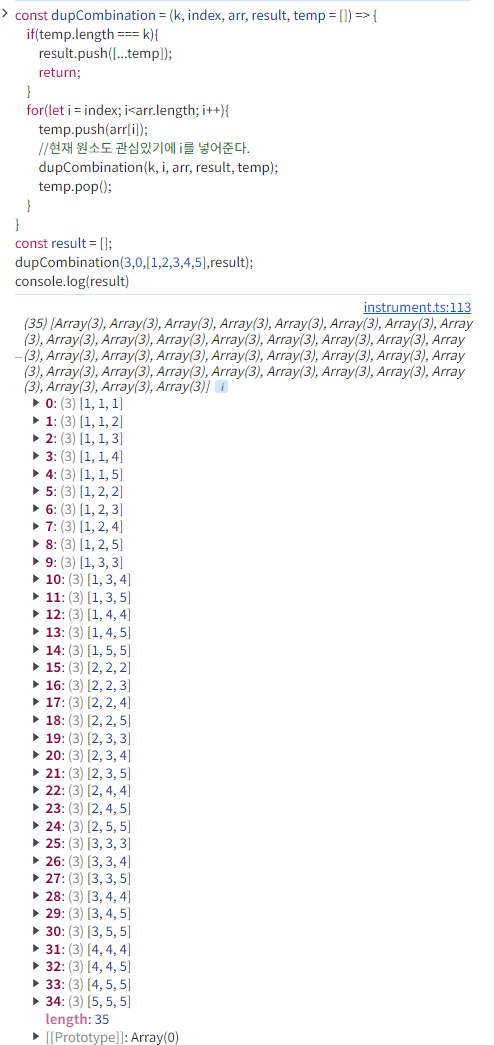

---

permutation

순열은 선택한 원소의 이전원소도 선택할수 있다는 점이 핵심이다.

1) 순열

즉, i번째 원소를 제외한 ...i-3, i-2, i-1, i+1, i+2, i+3...를 사용할 수 있다.
=> 순열은 현재 원소 방문체크가 필요하다.

const permutation = (k, arr, result, visited, temp = []) => {
	if(temp.length === k){
    	result.push([...temp]);
    	return;
    }
    for(let i = 0; i<arr.length; i++){
        if(visited[i]) continue;
    	temp.push(arr[i]);
        visited[i] = 1;
    	permutation(k, arr, result,  visited, temp); 
        visited[i] = 0;
      	temp.pop();
    }
}
const result = [];
const visited = Array(4).fill(0);
permutation(3,[1,2,3,4], result,visited); 

2) 중복순열

0~n번째 모두 방문 가능하다. 따라서 방문처리도 필요 없다.

const dupPermutation = (k, arr, result, temp = []) => {
	if(temp.length === k){
    	result.push([...temp]);
    	return;
    }
    for(let i = 0; i<arr.length; i++){
    	temp.push(arr[i]);
    	dupPermutation(k, arr, result, temp); 
      	temp.pop();
    }
}
const result = [];
dupPermutation(2,[1,2,3],result);
console.log(result);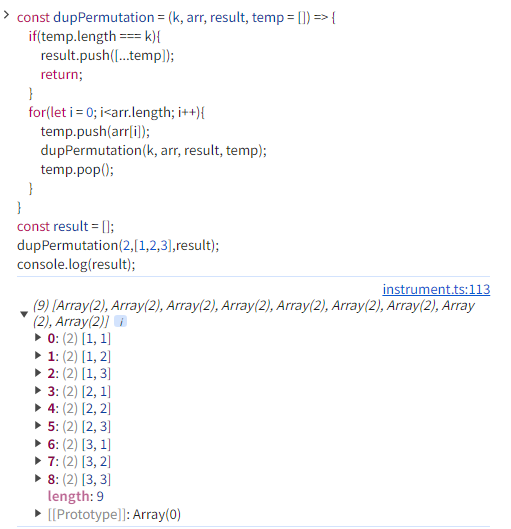

정리

• 조합은 현재 선택된 원소 이후의 인덱스(i+1)를 기반으로 재귀함수를 호출한다.
• 순열은 현재 선택된 원소를 제외한 모든 원소(인덱스 필요x 현재 원소 방문처리)를 상대로 재귀함수를 호출한다.
• 중복조합은 현재 선택된 원소의 인덱스(i) 기반으로 재귀함수를 호출한다.
• 중복순열은 모든 원소를 기반(방문처리 필요x)으로 재귀함수를 호출한다.