누적합
누적합은 DP라고 볼수있다. 특정 점화식을 구하여 상향식으로 접근한다. (메모이제이션 포함)
아래와 같은 예시를 보자.
예를들어 길이가 n인배열에서 [a,b]의 합을 구해야한다.
나이브하게 작성한다면 다음과 같은 알고리즘이 될 것이다.
const a = [1,2,3,4,5];
let sum = 0;
for(let i = a; i<=b; i++){
sum += a[i];
}위 알고리즘은 간단명료하고 잘 작동한다. 굳이 누적합이라는 알고리즘을 사용할 필요도 없다.
하지만 구간합을 10개, 100개, 1000개...를 구해야한다면?
구해야하는 구간합의 갯수가 m개일때 시간복잡도는 최대 n*m이 될 것이다.
이때 누적합은 진가를 발휘한다.
- 각 인덱스의 누적합을 구해준다.
- [a,b]구간이 주어진다면, 누적합[b]에서 누적합[a-1]를 빼주면 된다.
const a = [1,2,3,4,5];
const prefixes = [
[0,2],
[1,3],
....
]
const n = a.length
//누적합의 인덱스는 1-index를 사용한다
const prefixSum = Array(n + 1).fill(0);
prefixes[1] = a[0]
for(let i = 1; i<=n; i++){
prefixSum[i] += prefixSum[i-1] + a[i-1];
}
prefixes.forEach(([a,b]) => {
console.log(prefixSum[b] - prefixSum[a-1]);
})이전 값을 활용해서 시간복잡도를 O(n)으로 줄일 수 있게 되었다.
2차원 배열에서의 누적합
먼저 나이브하게 [r1,c1], [r2,c2]의 구간합을 계산해보자.
예시로 원하는 구간합이 [0,0],[1,1]이라고 가정해보자.
const a = [[31,2],[12,26]];
const [r1,c1,r2,c2] = [0,0,1,1]
const sum = 0;
for(let i = r1; i<=r2; i++){
for(let j = c1; j<=c2; j++){
sum += a[i][j];
}
}
console.log(sum) //71a가 N x N배열이라고 할때, M개의 구간합이 존재한다면, 최악의 경우 N x N x M의 시간이 걸린다.
이를 누적합을 통해 최적화해보자.
1차원 배열에서는 [a,b]의 합을 누적합[b] - 누적합[a-1]로 값을 구해냈다.
2차원 배열에서도 비슷하게 값을 구할 수 있지만, 중복해서 빠지는 값을 유의해야 한다.
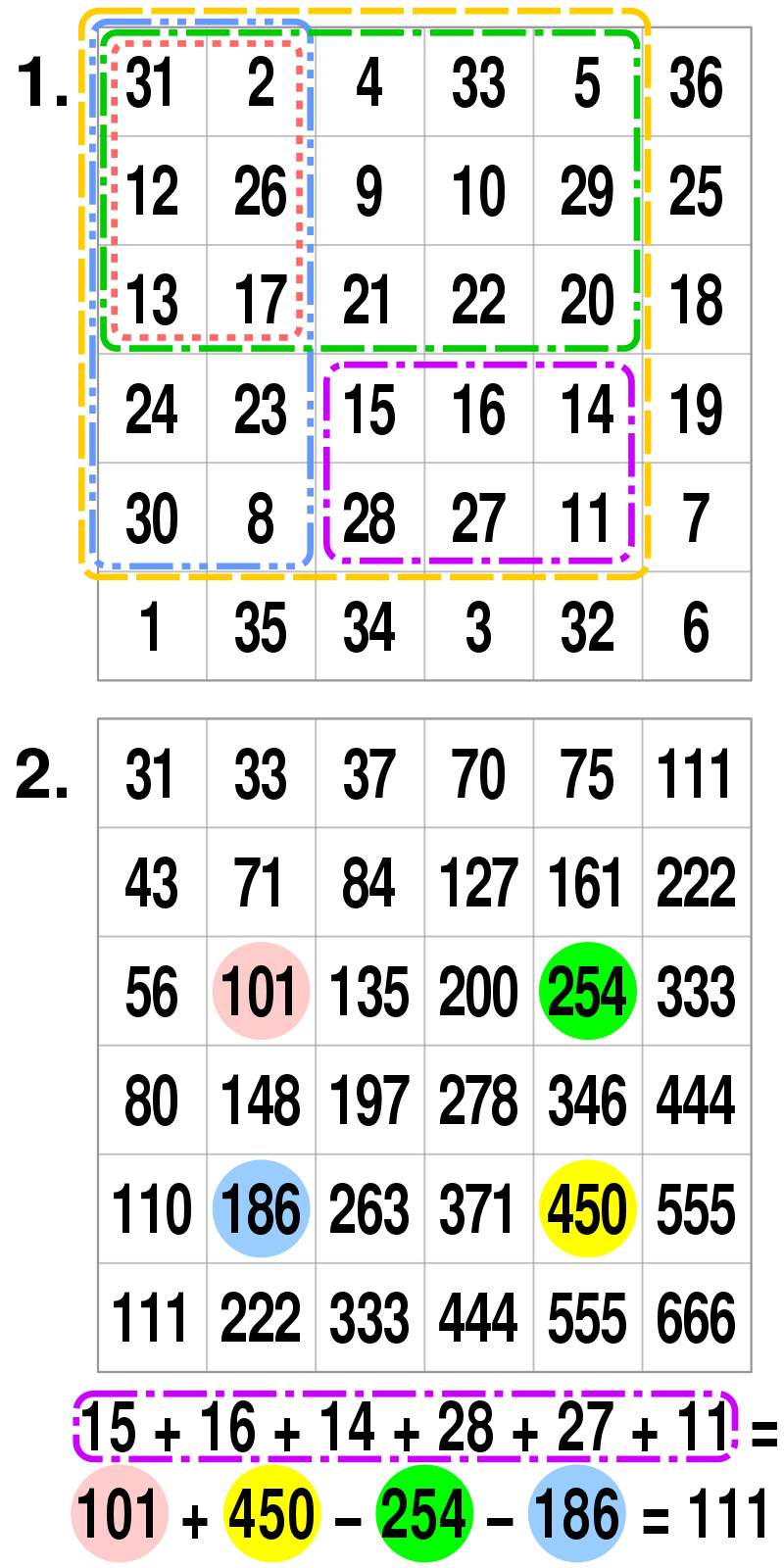
예시로 [2,1], [4,4]의 구간합을 구해보자.
- [4,4]까지 구간합을 구한다.
- 누적합[4,4]에서 누적합[2,4]와 누적합[4,1]를 빼준다.
- 중복해서 빠진 값인 누적합[2,1]을 한번 더해준다.
그림으로 보면 더 간단하다.
출처:https://en.wikipedia.org/wiki/Summed-area_table#/media/File:Integral_image_application_example.svg
위 누적합을 식으로 나타내면 아래와 같다.
//r1,c1,r2,c2 = 2,1,4,4
r1c2~r2c2누적합 = prefixSum[r2][c2] - prefixSum[r1][c2] - prefixSum[r2][c1] + prefixSum[r1][c1];코드로 변환해보자
const a = [
[31,2,4,33,5,36],
[12,26,9,10,29,25],
[13,17,21,22,20,18],
[24,23,15,16,14,19],
[30,8,28,27,11,7],
[1,35,34,3,32,6]
];
const prefixes = [
[1,1,2,3],
[2,1,4,4],
...
]
//누적합은 항상 1-index를 사용하면 편하다.
const prefixSum = Array.from({length:n+1}, () => Array(n+1).fill(0));
prefixSum[1][1] = a[0][0];
for(let i = 1; i<=n; i++){
for(let j = 1; j<=n; j++){
//테이블을 채우는 이 부분이 헷갈릴수도 있는데, 아까 누적합을 식으로 나타낸걸 생각해보자.
//0,0 ~ i,j까지 누적합을 구한다고 하면, 왼쪽 누적합 + 위 누적합 + 현재값 - 중복해서 더해진 값 으로 나타낼 수 있다.
prefixSum[i][j] = prefixSum[i][j-1] + prefixSum[i-1][j] + a[i-1][j-1] - prefixSum[i-1][j-1];
}
}
prefixes.forEach(([r1,c1,r2,c2]) => {
console.log(prefixSum[r2][c2] - prefixSum[r2][c1] - prefixSum[r1][c2] + prefix[r1][c1]);
})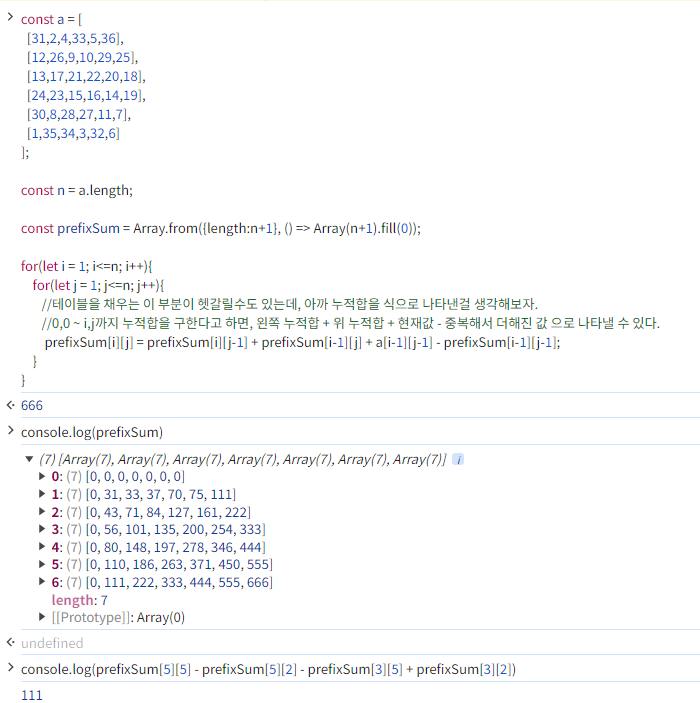
항상 헷갈렸는데 정리하니까 머릿속에 쏙속 들어오는구먼?
imos
구간 중첩관련 계산할때 유용한 알고리즘이다. 누적합과 거의 유사하다.
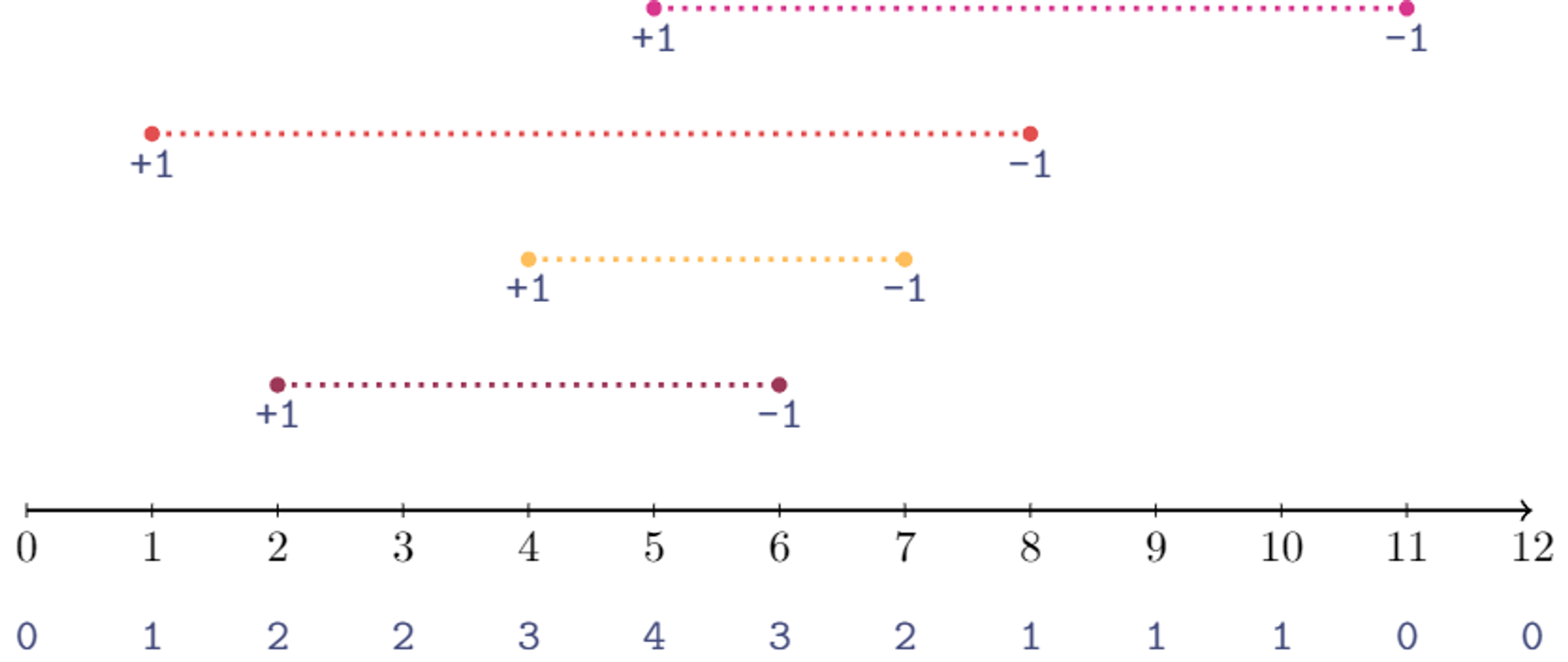
예를들어 아래와 같은 그림을 보자.
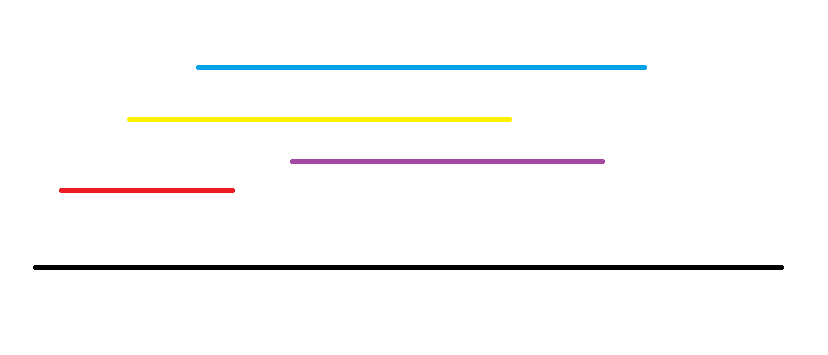
x축은 값, 형형색색 선들은 구간이다.
특정 구간[a,b]가 주어지고 구간 내 최대 중첩 된 선분을 구하고싶다.
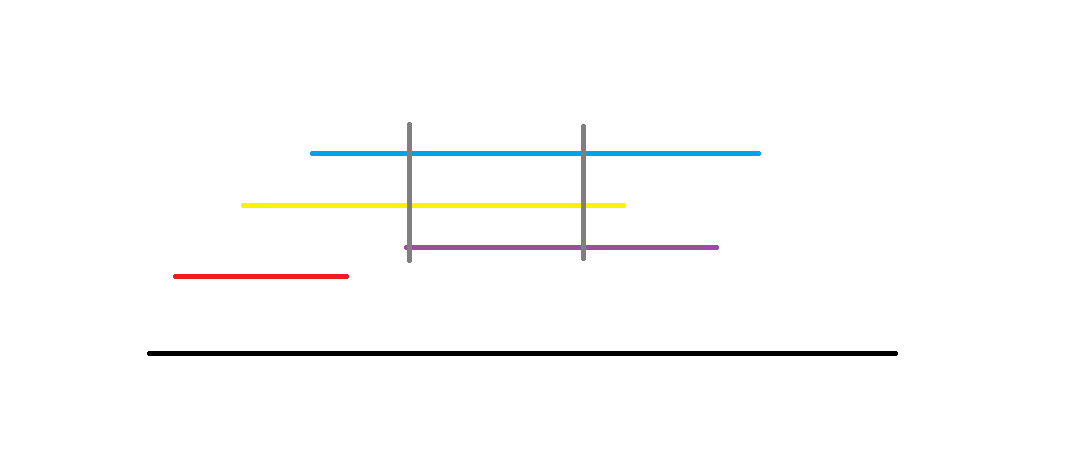
만약 주어진 구간이 회색 선분일때 최대 중첩 선분은 위 그림처럼 될 것이다.
이걸 어떻게 구해볼까?
1차원 배열 imos
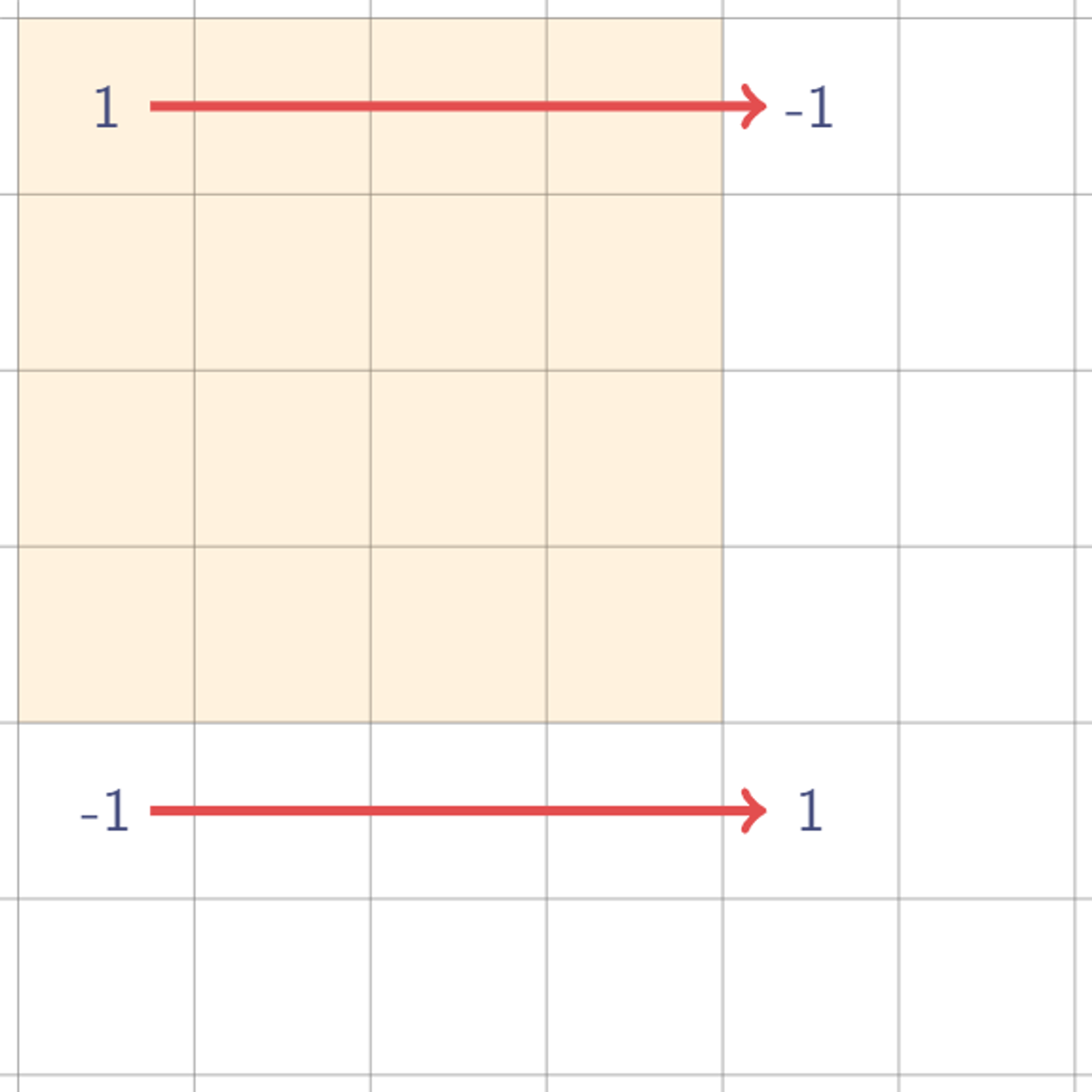
- 각 선분의 끝과 시작지점에 1, -1을 찍는다. (선분의 시작, 끝만 기록해둔다)
- 이후 값을 갱신한다. 이때 누적합과 비슷하게 이전 인덱스의 값을 더해준다. (누적합)
2차원 배열 imos
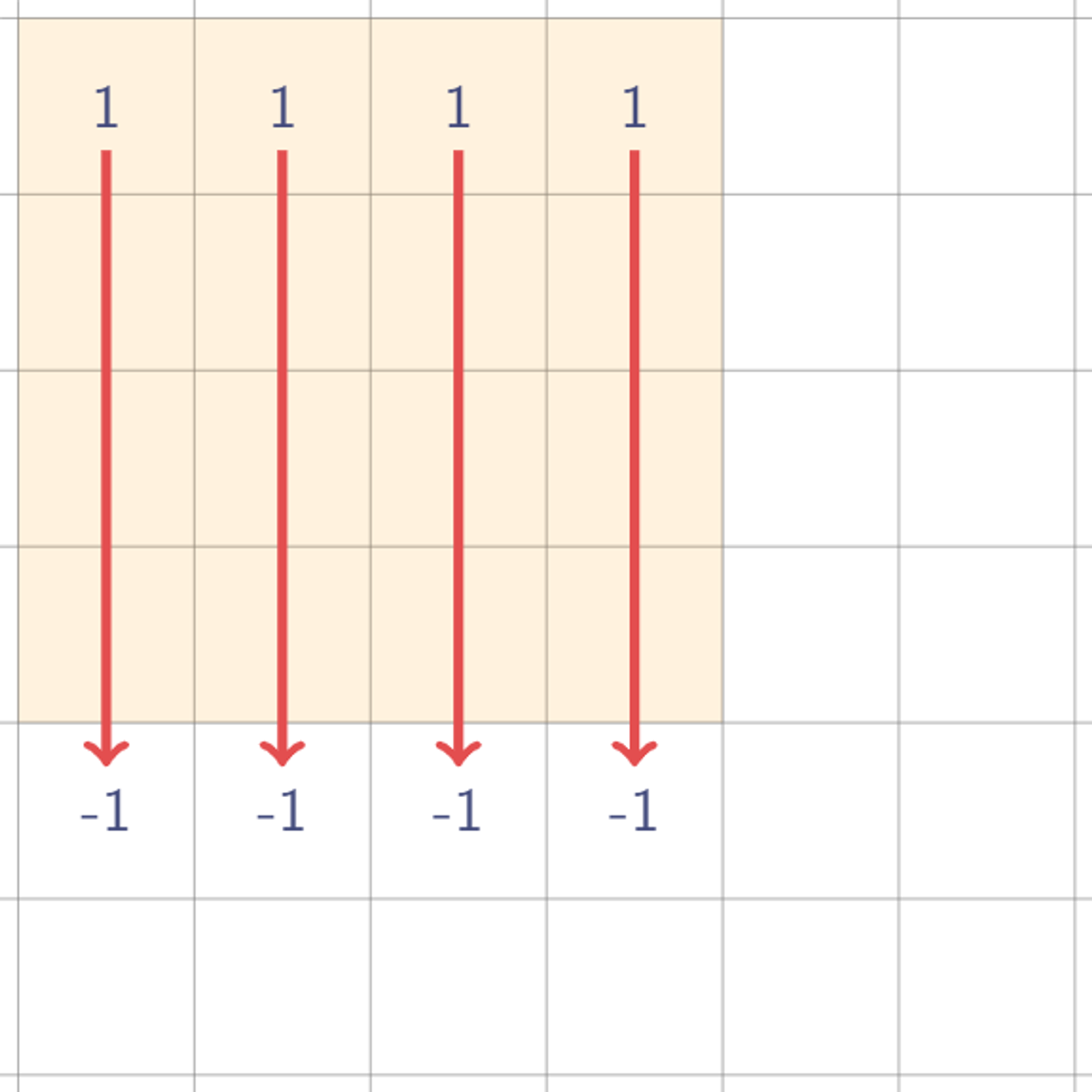
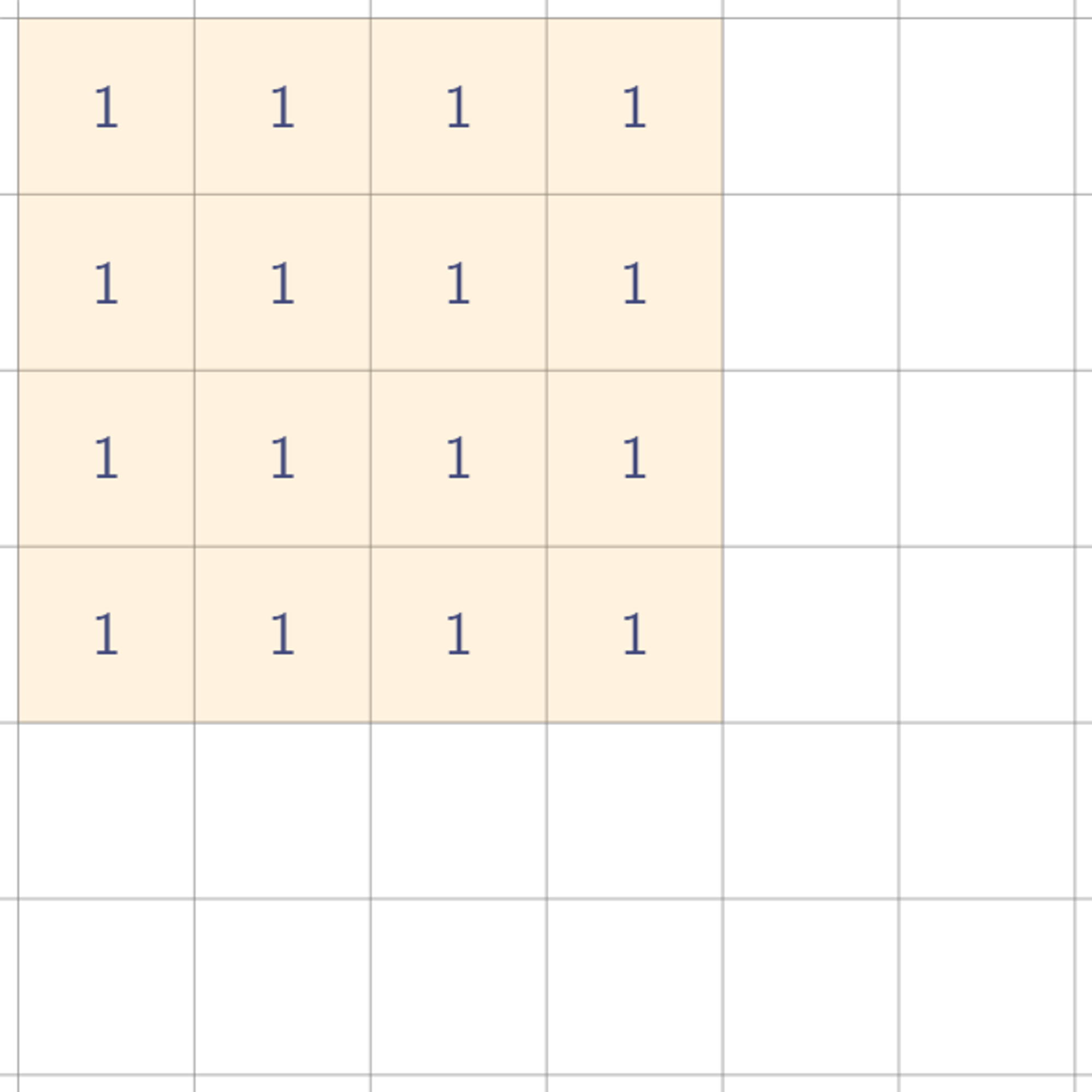
- [r1,c1]과 [r2+1,c2+1]에 1을 찍고 [r1,c1+1], [r2,c1+1]에 -1을 찍는다.
- 이후 열 누적합을 구한 뒤 행 누적합을 구한다.
이미지 세개 출처 : https://driip.me/65d9b58c-bf02-44bf-8fba-54d394ed21e0
imos 관련 문제
https://school.programmers.co.kr/learn/courses/30/lessons/92344
단순한 누적합으로 구할때는 힘들었으나, imos를 알고난뒤 정말 빨리 풀린 문제다.
function solution(board, skill) {
const [r,c] = [board.length+1, board[0].length+1];
const nBoard = Array.from({length:r}, () => Array(c).fill(0));
for(let i = 0; i < r-1; i++){
for(let j = 0; j< c-1; j++){
nBoard[i][j] = 0;
}
}
skill.forEach(([type,r1,c1,r2,c2,degree]) => {
if(type === 1){
degree = -degree;
}
nBoard[r1][c1] += degree;
nBoard[r2+1][c2+1] += degree;
nBoard[r1][c2+1] -= degree;
nBoard[r2+1][c1] -= degree;
})
//열 기준 누적합
for(let i = 0; i<r; i++){
for(let j = 1; j<c; j++){
nBoard[i][j] += nBoard[i][j-1];
}
}
//행 기준 누적합
for(let j = 0; j<c; j++){
for(let i = 1; i<r; i++){
nBoard[i][j] += nBoard[i-1][j];
}
}
let result = 0;
for(let i = 0; i<r-1; i++){
for(let j = 0; j<c-1; j++){
nBoard[i][j] += board[i][j];
if(nBoard[i][j]>0) result++
}
}
return result;
}뻐팅기지 말자
알고리즘을 모르고 푸는게 능사는 아니다. 알고리즘과 자료구조를 최대한 습득한 뒤 풀자. 모른 채 푸는 것도 재밌지만, 알아야 풀린다!