플로이드-워셜 알고리즘

최단거리를 구하는 대표적인 알고리즘 두가지중 하나다.

• 모든 정점 쌍 사이의 최단거리를 구하는 알고리즘이다.
• 모든 정점 간의 최단거리를 구하기때문에 시간복잡도가 크다. O(V^3) => 보통 n이 1000까지는 가능하다.
• 핵심은 start에서 to로 가는 거리 vs start, via + via, to로 가는거리를 비교하는 것이다.

예시문제) 플로이드

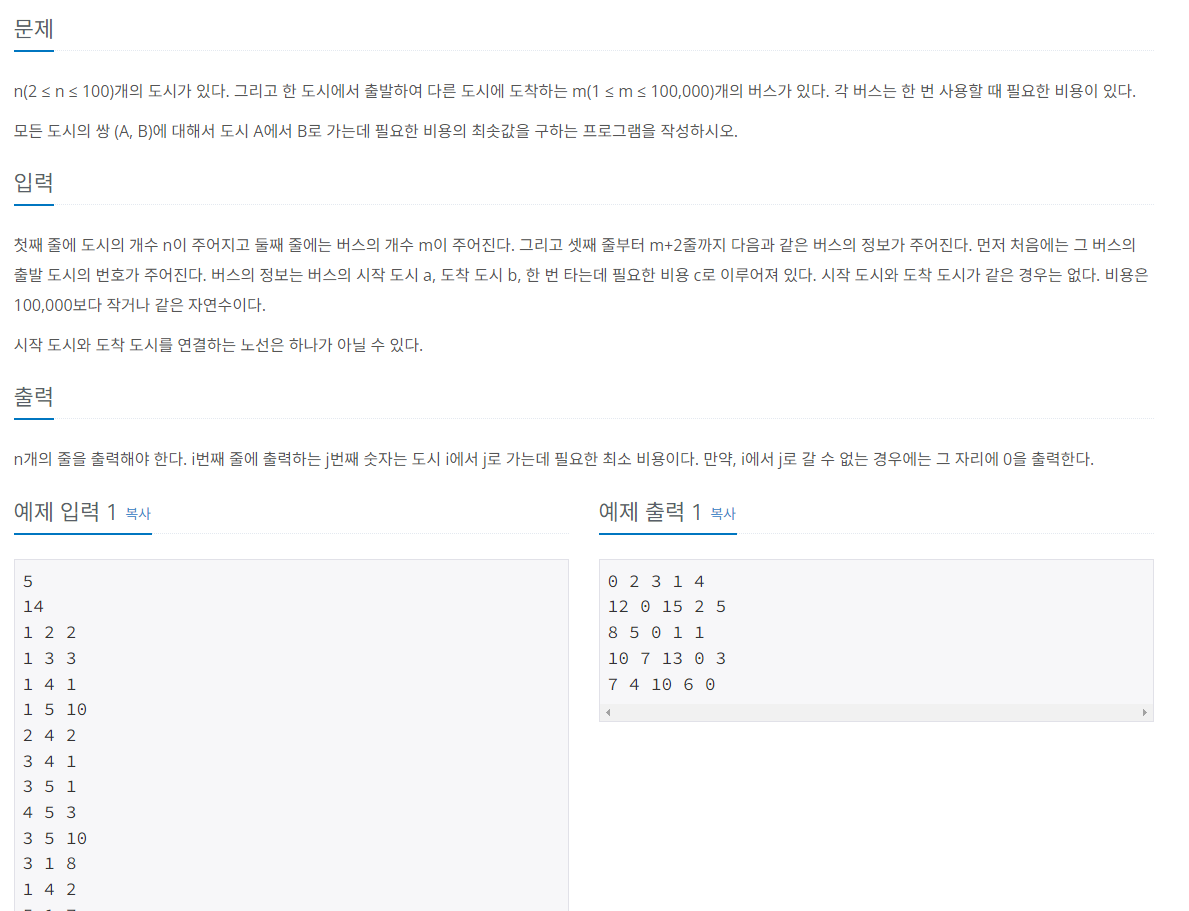
구현할때 주의해야할 점은 거쳐가는 지점을 맨 바깥 for문에 지정해주어야한다.

const input = require("fs")
  .readFileSync("example.txt")
  .toString()
  .trim()
  .split("\n")
  .map((el) => el.trim().split(" ").map(Number));

const [[n], [m]] = input.splice(0, 2);

const distance = Array.from({ length: n + 1 }, () =>
  Array(n + 1).fill(Number.MAX_SAFE_INTEGER)
);

input.forEach(([start, to, cost]) => {
  distance[start][to] = Math.min(distance[start][to], cost);
});

for (let i = 1; i <= n; i++) {
  distance[i][i] = 0;
}

for (let via = 1; via <= n; via++) {
  for (let start = 1; start <= n; start++) {
    for (let to = 1; to <= n; to++) {
      distance[start][to] = Math.min(
        distance[start][to],
        distance[start][via] + distance[via][to]
      );
    }
  }
}

let result = "";

for (let i = 1; i <= n; i++) {
  for (let j = 1; j <= n; j++) {
    if (distance[i][j] === Number.MAX_SAFE_INTEGER) {
      result += "0 ";
    } else {
      result += `${distance[i][j]} `;
    }
  }
  result.trim();
  result += "\n";
}

console.log(result.trim());

다익스트라 알고리즘

최단거리 알고리즘 중 하나!

• 하나의 시작점으로부터 다른 모든 정점까지의 최단거리를 구하는 알고리즘이다.
• 음수 간선이 있을땐 사용할 수 없다.
• 현재 갈수있는 정점중에서 최단거리인 정점을 갱신해주면 된다.

다익스트라 구현

const adj = [[],[{to:1, dist:5},{...}],...];
const dist = Array(n).fill(Number.SAFE_MAX_INTEGER);

const q = [];
q.push(adj[start]);

dist[start] = 0;

//이부분은 원래 우선순위큐로 구현해야함...
while(q.length){
  const to = q.shift();
  adj[to].forEach((next) => {
    //next는 {to:1, dist:5}
    const acc = dist[to] + next.dist;
    //짧은거리일때만 갱신해준다
    if(dist[next.to] > acc){ //방문 노드까지 이동한 거리 + 다음 방문까지 노드 거리를 기존 노드거리와 비교
      dist[next.to] = acc;
      q.push(next);
    }
  })
}