위상정렬

위상정렬은 들어보기만 했고 아예 모르는 알고리즘이다! 위상정렬은 대체 뭘까?

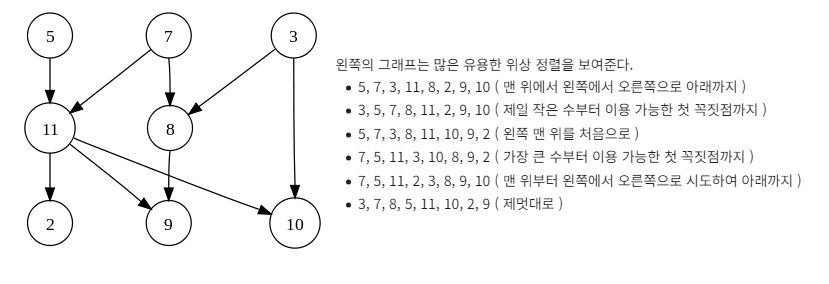
• 방향 그래프에서 간선으로 주어진 정점 간 선후 관계를 위배하지 않도록 나열하는 정렬.

출처

아하 그러니까 방향 그래프에서 출발 정점이 도착 정점보다 앞에 오는 정렬이다.

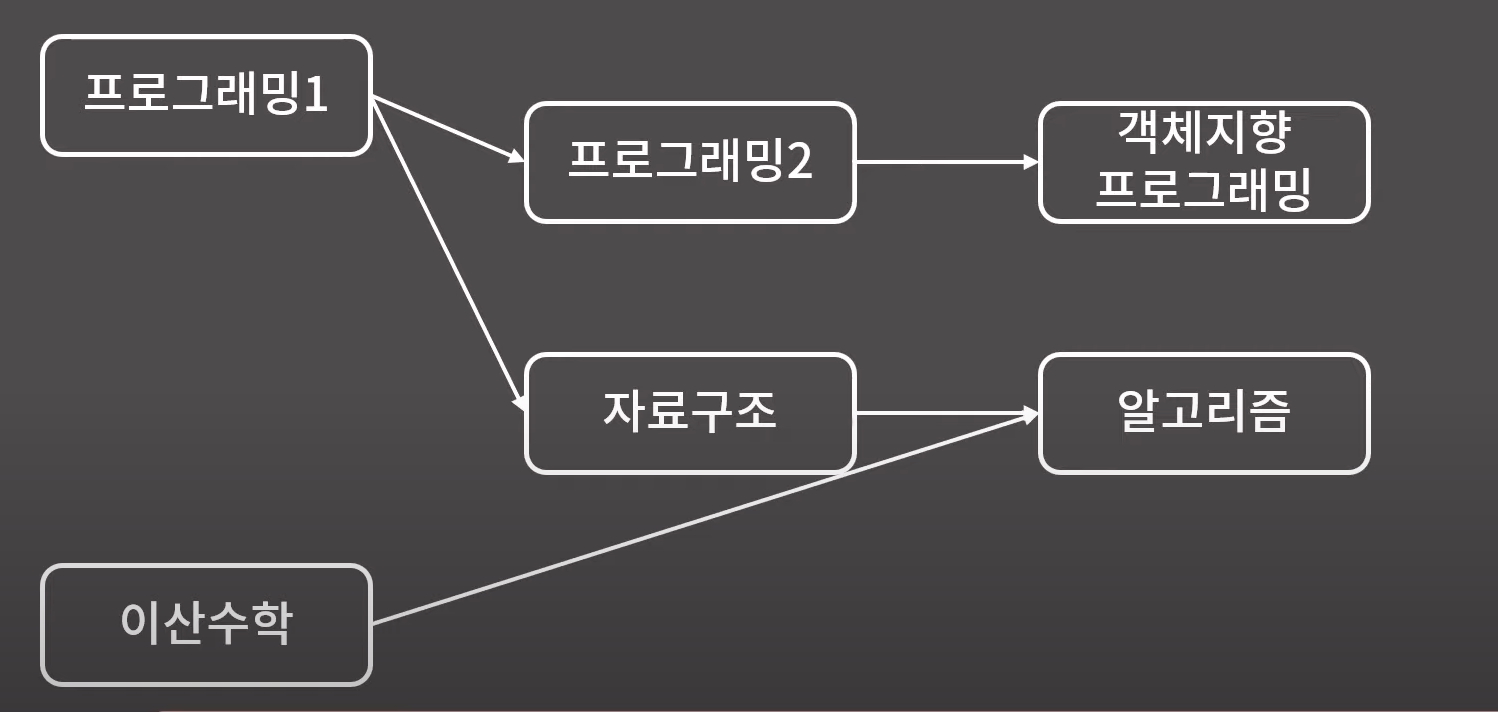
쉽게 설명하자면 선수 과목을 생각해보면 된다. 특정 과목을 이수해야만 수강 할 수 있는 과목이 있다.
이 과목들을 위상정렬 했을 시, 선수 과목을 지킨 정렬이 위상정렬이다.

출처

다만 위상정렬은 사이클이 존재하면 할 수 없다. 또한 위상정렬된 결과는 여러개일 수 있다.

위상정렬의 구현

1. indegree가 없는 정점을 고른다.
2. 그 정점과 정점에서 뻗어나가는 간선을 제거한다.
3. 1번을 반복.

이름만 들었을땐 어려워 보였지만, 생각한 것 보다 쉽다. 다만 효율적으로 구현해야한다.

• 정점과 간선을 실제로 지우지 않고 indegree의 값을 저장했다가 뻗어나가는 정점들의 indegree값만 1씩 감소시킨다.
• indegree가 0인 정점을 구할땐 매번 모든 정점을 확인하는 게 아닌, 목록을 따로 저장해두어 직전에 제거한 정점에서 연결된 정점만 추가한다.

위 사항을 지키면 다음과 갇타.

1. 맨 처음 모든 간선을 읽으며 indegree를 저장한다.
2. indegree가 0인 정점을 모두 큐에 넣는다.
3. 큐에서 정점을 꺼내 위상정렬 결과에 추가한다.
4. 해당 정점으로부터 연결된 모든 정점의 indegree값을 1 감소시킨다(1번에서 저장한 값) 이때 indegree가 0이되었다면 그 정점을 큐에 추가한다.
5. 큐가 빌때까지 3,4번과정을 반복한다.

이를 코드로 옮겨보자.

//1~n까지 정점
const adj = [...];
const indegrees = [...]; //각 정점 indegree

const q = [];
const result = [];

for(let i = 1; i<=n; i++){
  if(indegrees[i] === 0) q.push(i);
}

while(q.length){
  const cur = q.shift();
  result.push(cur);
  for(const next of adj[cur]){
    indegress[next]--;
    if(indegrees[next] === 0) q.push(next);
  }
}

if(result.length !== n) return console.log('사이클 존재');

return result;

그래프에서의 BFS,DFS처럼 시간복잡도는 O(V+E)다. 왜 그럴까?
=> 각 정점은 큐에 한 번 들어가고 indegree감소연산은 각 간선에대해 한번 발생한다.

위상정렬 문제) 줄세우기

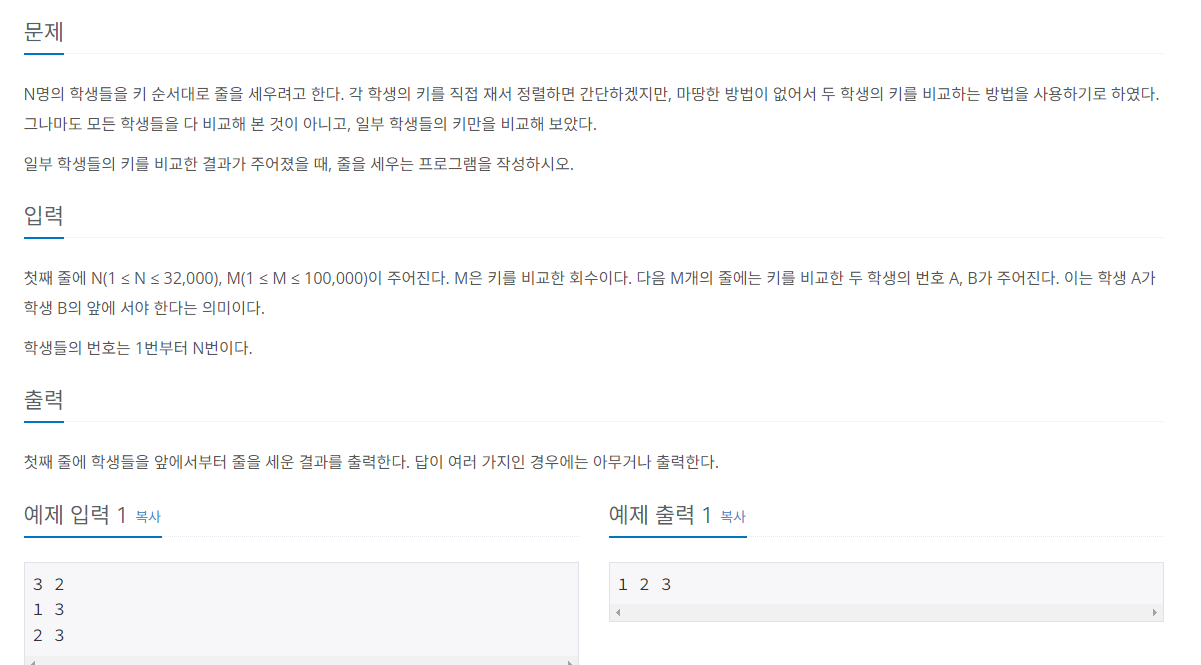
보자마자 위상정렬을 떠올릴 수 있어야 한다. 작은 학생이 큰 학생보다 앞에 있어야 한다는 건, 방향그래프를 뜻한다.

const input = require("fs")
  .readFileSync("example.txt")
  .toString()
  .trim()
  .split("\n")
  .map((el) => el.trim().split(" ").map(Number));

const [n, m] = input[0];

const adj = {};
const deg = Array(n + 1).fill(0);

const q = [];
const result = [];

for (let i = 1; i <= n; i++) {
  adj[i] = [];
}

for (let i = 1; i <= m; i++) {
  const [short, long] = input[i];
  adj[short].push(long);
  deg[long]++;
}

for (let i = 1; i <= n; i++) {
  if (deg[i] === 0) q.push(i);
}

while (q.length) {
  const cur = q.shift();
  result.push(cur);
  for (const next of adj[cur]) {
    deg[next]--;
    if (deg[next] === 0) q.push(next);
  }
}

console.log(result.join(" "));

해결!

---

최소 신장 트리(MST)

최소 신장트리를 알아보기전에 신장트리가 무엇인지 부터 알아야 한다.

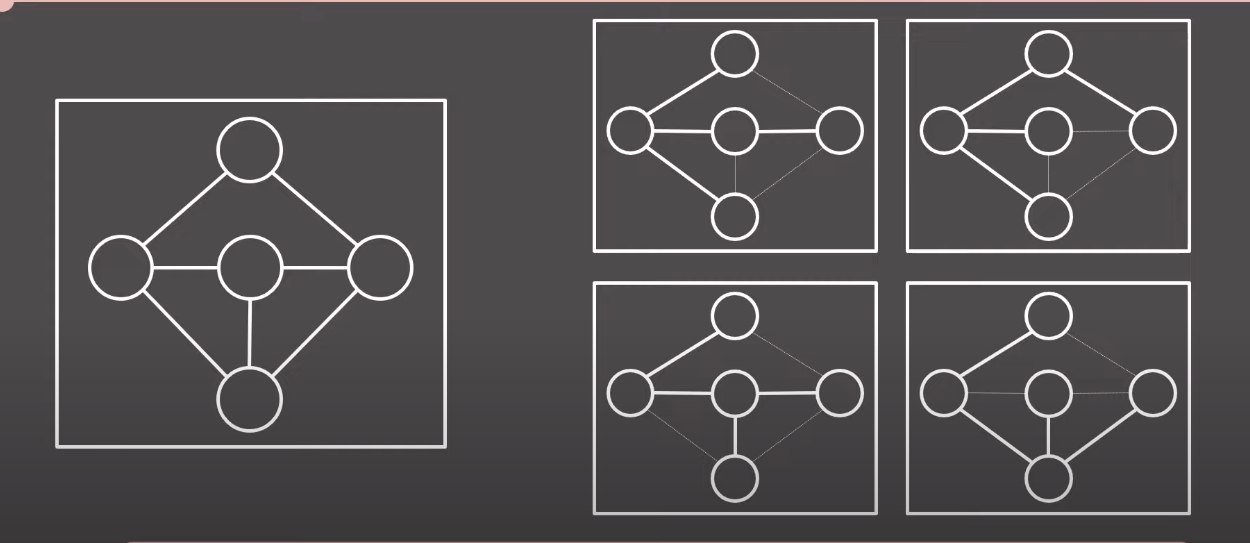
• 신장트리란 방향성이 없는 그래프의 부분 그래프중에서 모든 정점을 포함하는(연결된) 트리다.

출처

• 최소신장트리란 신장 트리중 간선의 합(가중치, 거리 등...)이 최소인 트리를 의미한다. 결과가 여러개일 수 있다.

크루스칼 알고리즘(union find)

MST를 구할때 사용하는 대표적인 알고리즘이다. 하지만 Union Find알고리즘을 알아야 이 알고리즘을 익힐 수 있다.
그래서 Union Find알고리즘 부터 알아보자!

유니온파인드 사진의 출처는 여기입니다!

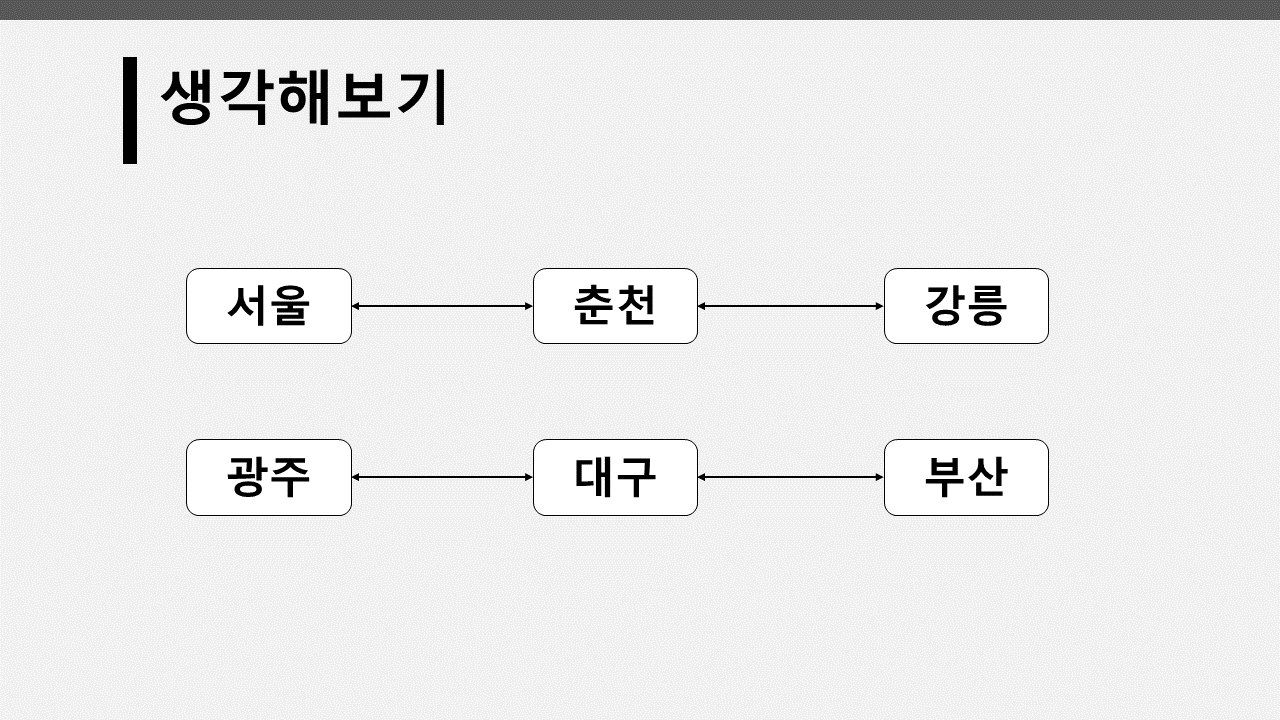
서울 => 강릉은 갈 수 있지만, 서울 => 부산 은 갈 수 없다. 왜?
=> 이어져 있지 않고든

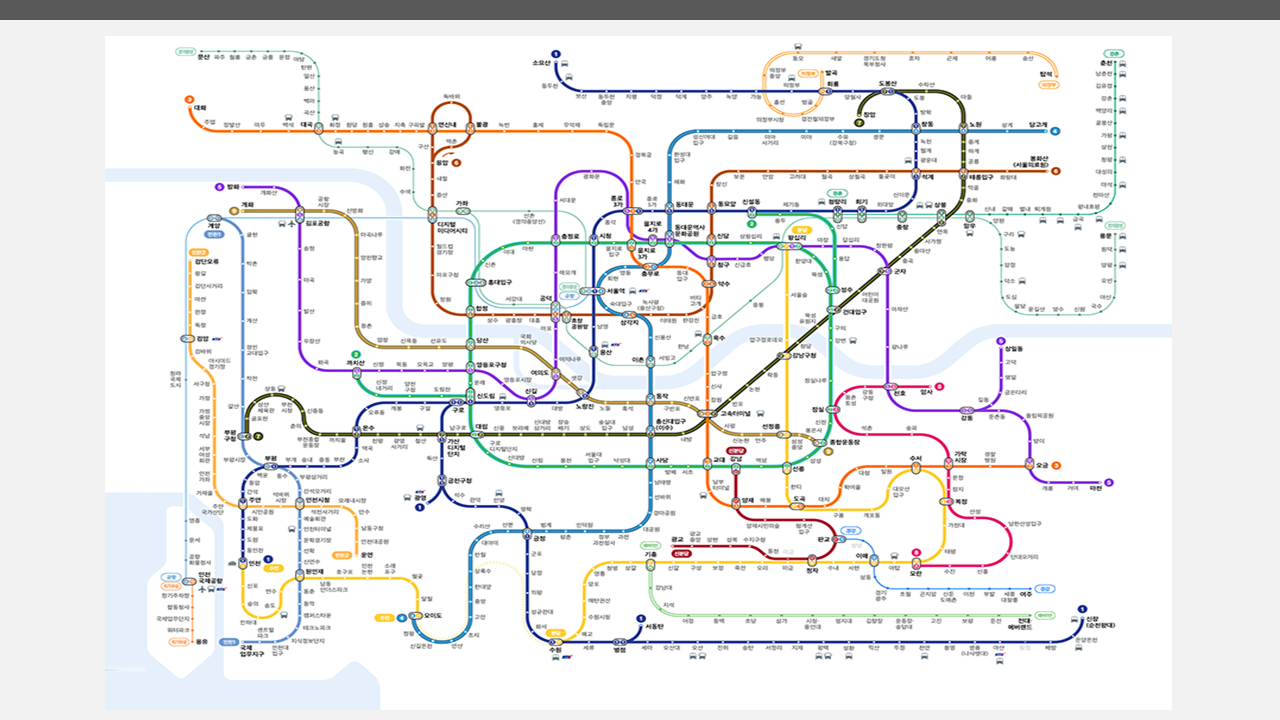
이렇게 복잡한 노선도라면 직관적으로 판별 불가능하다. 이때 사용하는게 Union find(상호 배타 집합 찾기)다.

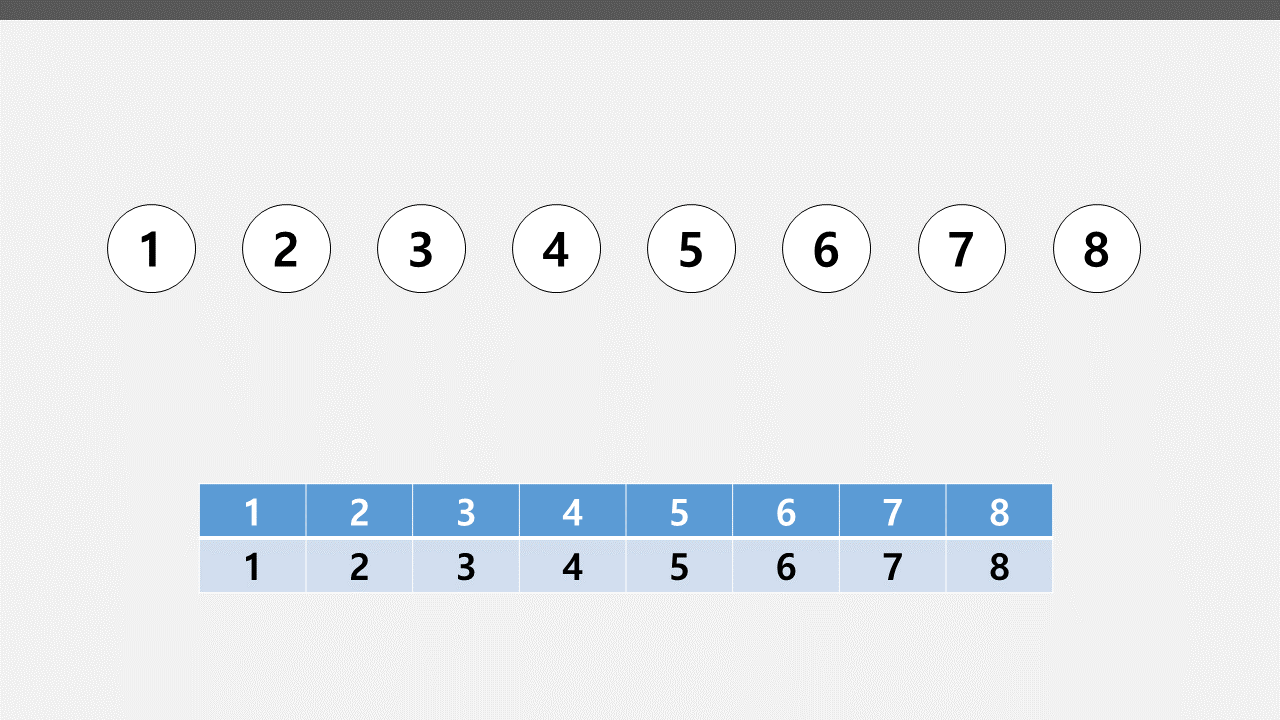
먼저 모든 노드를 초기화(홀로 떼어버림)한다. 이때, 부모는 자기 자신이다.

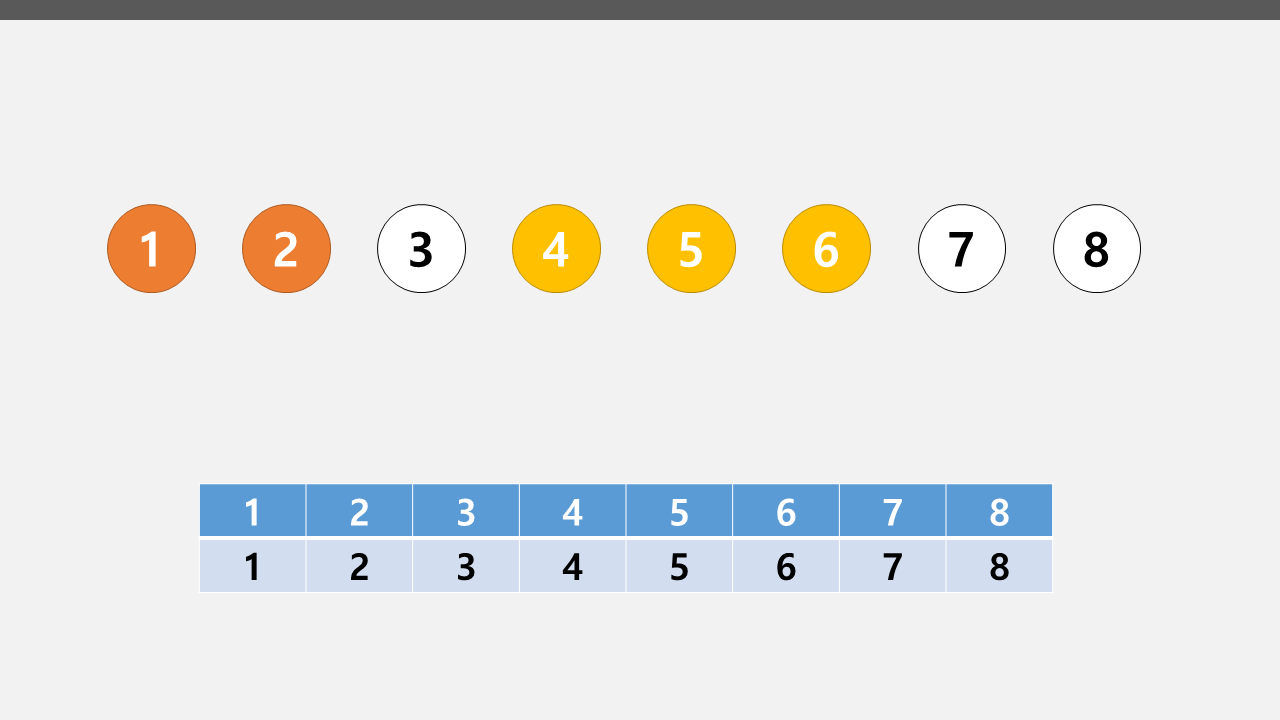
만약 1-2노드를 연결하고 4-5-6노드를 연결하고싶다면 아래처럼 하면 된다.

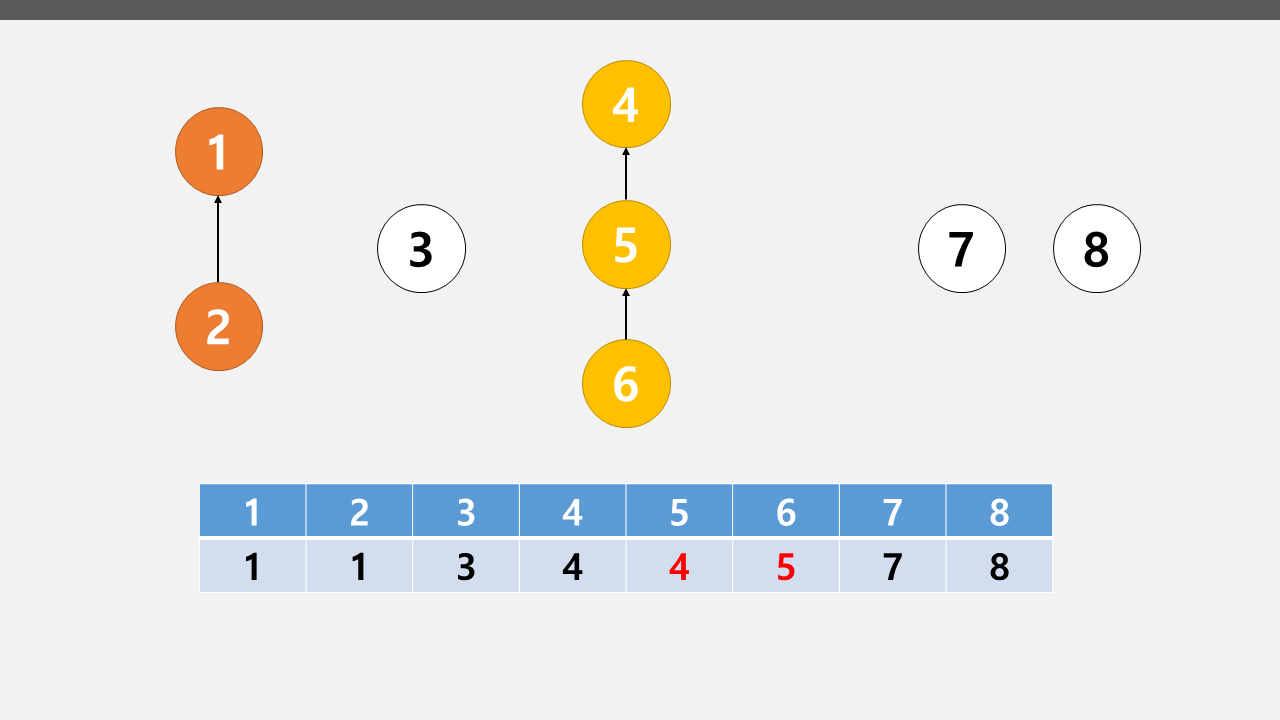
이런식으로 연결 한 뒤, 부모를 나타내는 값을 배열에 적어준다.
하지만 이렇게 바로 윗 부모를 배열에 적어주면 가끔 문제가 발생한다.

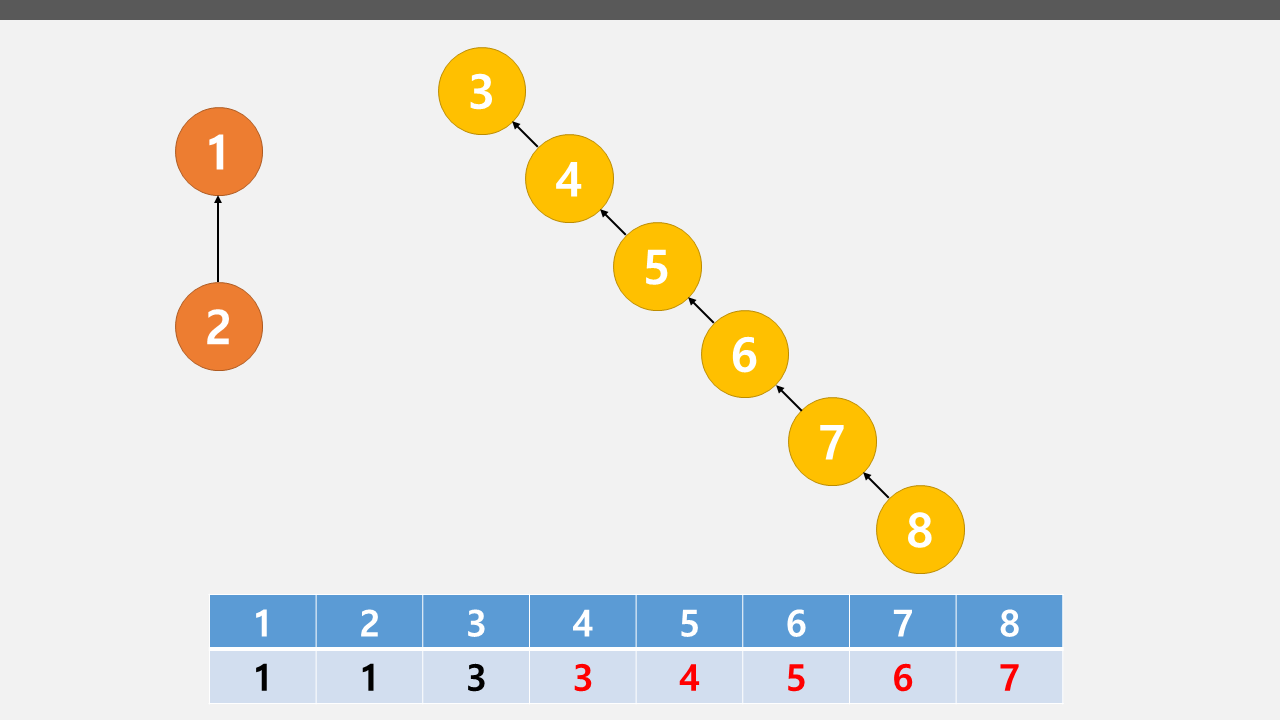
이렇게 극단적인 트리가 존재한다면...부모까지 O(n)만큼의 시간이 걸릴 것이다.
따라서 바로 윗 부모가 아닌, 루트를 기록해둔다면 판단하기 쉬울 것이다.

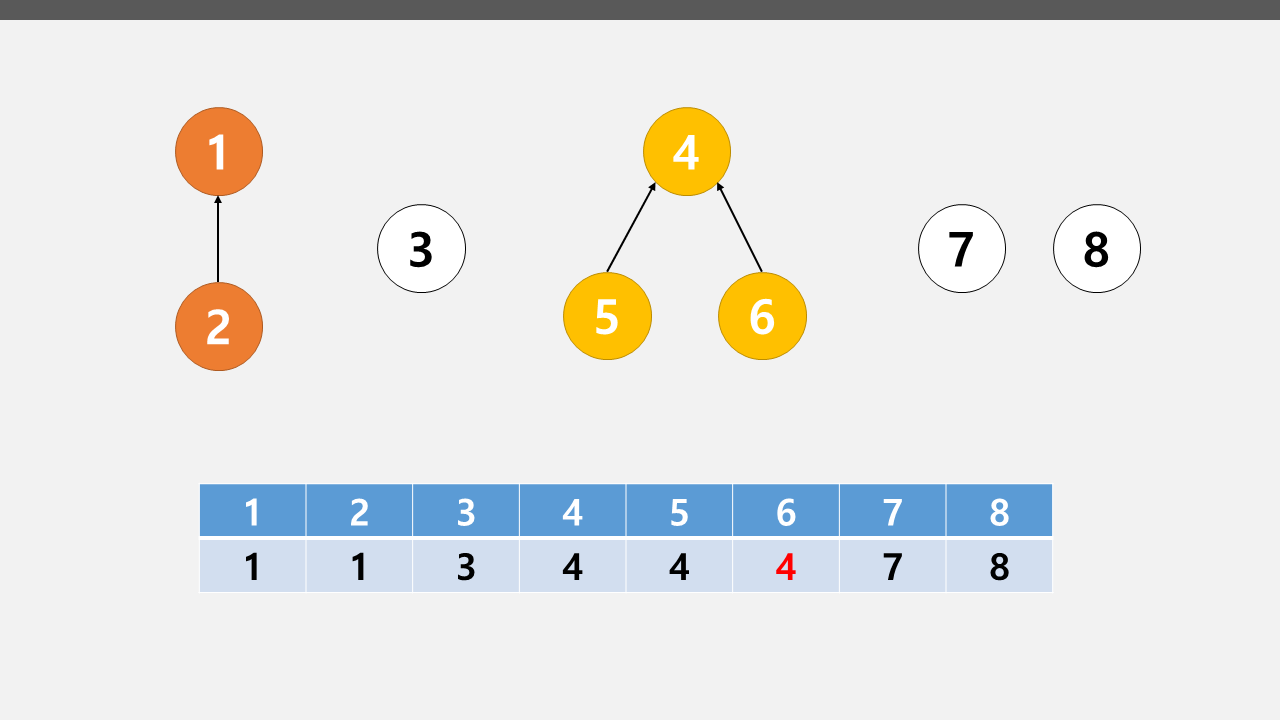
요래말이다.

위 그림을 이제 코드로 옮겨보자!

//초기화 과정. 자기 자신이 부모다.
const init = (N) => {
  return Array(N)
    .fill(0)
    .map((value, idx) => idx);
};

//부모를 탐색하는 과정. 
const findParent = (x, parent) => {
  if (parent[x] === x) { //배열 인덱스와 값이 같으면 루트다
    return x;
  };
  return parent[x] = findParent(parent[x], parent); //배열의 값을 인덱스로 갖는 값을 리턴
};

const union = (A, B, parent) => {
  const rootA = findParent(A, parent);
  const rootB = findParent(B, parent); //각자 루트노드를 가진다.

  rootA < rootB ? (parent[rootB] = rootA) : (parent[rootA] = rootB);
};

const isDiffParent = (parent, x, y) => {
  return findParent(parent,x) === findParent(parent,y)
}

이제 크루스칼 알고리즘을 배워보자

크루스칼 알고리즘

1. 간선을 크기의 오름차순으로 정렬 후 제일 낮은 비용 간선 선택
2. 현재 선택한 간선이 정점 u,v를 연결하는 간선이라고 할 때 u,v가 같은 그룹이면 패스, 다른 그룹이라면 같은 그룹으로 만들고 현재 선택한 간선을 최소 신장 트리에 추가
3. 최소신장 트리에 V-1개의 간선을 추가시켰다면, 과정을 종료. 그렇지 않다면 그 다음으로 비용이 작은 간선을 선택 후 2번과정을 반복.

const e,v //간선갯수, 정점갯수
const edge = Array({length:e}, () => [비용, 정점1, 정점2]);
const parent = []

edge.sort((a,b) => a[0] - b[0]) //제일 비용이 낮은 간선순으로 정렬;

let cnt = 0;

for(let i = 0; i< e; i++){
  const [cost, a, b] = edge[i];
  if(!isDiffParent(parent,a,b)) continue;
  console.log(a,b);
  cnt++;
  if(cnt === v-1) break;
}

---

프로그래머스 - 섬 연결하기(크루스칼)

MST를 찾는 문제다. 당연히 크루스칼을 사용하면 쉽게 풀린다.

function solution(n, costs) {
    const init = (n) => Array(n).fill(0).map((el,idx) => idx);
    const parent = init(n+1);
    const find = (x,parent) => {
        if(parent[x] === x) return x;
        return parent[x] = find(parent[x], parent);
    }
    
    const union = (a,b,parent) => {
        const rootA = find(a,parent);
        const rootB = find(b,parent);
        
        rootA < rootB ? (parent[rootB] = rootA) : (parent[rootA] = rootB);
    }
    
    const isSameParent = (parent,x,y) => find(x,parent) === find(y,parent);
    
    const e = costs.length;
    
    costs.sort((a,b) => a[2] - b[2]);
    
    let cnt = 0;
    
    let result = 0;
    
    for(let i = 0; i < e; i++){
        const [start,to,cost] = costs[i];
        if(isSameParent(parent,start,to)) continue;
        union(start,to,parent);
        cnt++;
        result += cost;
        if(cnt === n-1) break;
    }
    return result;
}

하지만 의문이 하나 남아있었다. 어차피 그리디하게 짧은 비용의 간선만 추가하면 되는데, 그러면 conneceted라는 배열을 하나 선언해서 union-find없이 사용할수 있지 않을까?

바로 실험해보았다.

function solution(n, costs) {
    const connected = Array(n+1).fill(0)

    costs.sort((a,b) => a[2] - b[2]);
    
    let cnt = 0;
    
    let result = 0;
    
    for(let i = 0; i < costs.length; i++){
        const [start,to,cost] = costs[i];
        if(connected[start] && connected[to]) continue;
        connected[start] = 1;
        connected[to] = 1;
        cnt++;
        result += cost;
        if(cnt === n-1) break;
    }
    return result;
}

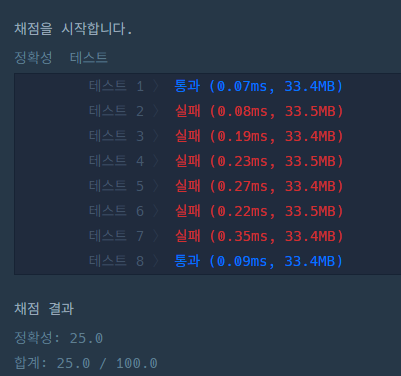
곰곰히 생각해보면, 두번째 코드는 cycle을 고려하지 않는다. 결국 cycle이 형성되면 최소 스패닝트리를 만족하지 않는다.

궁금증 해결!