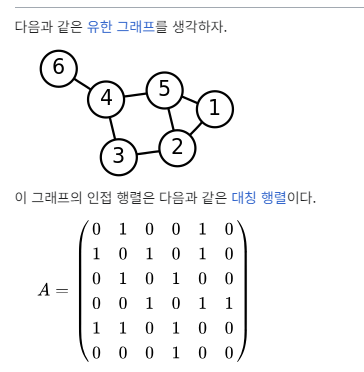
그래프
그래프는 알고리즘은 아니고 자료구조다. 어떤 자료구조일까?
- 정점과 간선으로 이루어진 자료구조 => 정점과 간선이 존재하면 그래프다!
- 차수(degree)는 각 정점에 대해서 간선으로 연결된 이웃한 정점의 개수다!
- 방향이나 가중치가 존재할 수 있다!
- 방향그래프에서 나가는 간선은 out-degree, 들어오는 간선은 in-degree다!
- 임의의 한 점에서 출발해 자기자신으로 돌아올 수 있는 경로를 cycle이라고 한다.
- 하나라도 있으면 순환그래프 없으면 비순환그래프다
- 서로 다른 모든 두 정점이 간선으로 연결된 그래프는 완전 그래프.
- 임의의 두 정점 사이에 경로가 항상 존재하면 연결 그래프
정의가 많다...!! 하나씩 잘 알고있어야 어떤 문제가 나오던 대응이 가능하다. 꼭꼭 씹어먹자.
그래프의 표현법1) 인접 행렬
행렬로 그래프를 어떻게 표현할까? 바로 각 정점을 행과 열로 나타낸다.
이를 코드로 나타내면 다음과 같다
//보통 아래와 같이 그래프의 연결 점이 주어진다.
const connections = [
[1, 5],
[1, 2],
[2, 5],
[2, 3],
[3, 4],
[4, 6]
];
const adjacencyMatrix = Array.from({ length: numNodes }, () => Array(numNodes).fill(0));
//무방향 그래프는 양쪽 다. 방향 그래프라면, node2 => node1로 가는길은 표시하지 않아도 된다.
connections.forEach(([node1, node2]) => {
adjacencyMatrix[node1 - 1][node2 - 1] = 1;
adjacencyMatrix[node2 - 1][node1 - 1] = 1;
});
/*
adjacencyMatrix = [
[0, 1, 1, 0, 1, 0],
[1, 0, 0, 0, 1, 0],
[1, 0, 0, 1, 0, 0],
[0, 0, 1, 0, 0, 1],
[1, 1, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0]
]
*/
이렇게 표현했을때의 장점은 뭐가있을까?
- 두 정점이 연결되었는지 확인하는데 O(1)만큼 소요된다! 획기적이구만
- 어떤 한 점에 연결되어있는 모든 정점을 확인할때도 정점의 갯수O(V)만큼만 소요된다.
단점은?
- 정점의 갯수^2 O(V^2) 만큼 공간이 필요하게 된다.
즉, 두 점의 연결여부를 자주확인하거나 간선의 개수가 정점^2에 가까울때 유리하다.
그래프의 표현법2) 인접 리스트
인접한 노드를 리스트로 나타낸다. 행렬도 사실 배열(리스트)긴 한데....😅
정점이 많은데 간선이 적은경우 유리하다.
- V개의 리스트를 만들어 인접한 정점의 번호를 넣는다.
- 인접한 정점의 번호만 넣으면 되니, O(V+E)의 공간이 필요하게 된다.
const connections = [
[1, 5],
[1, 2],
[2, 5],
[2, 3],
[3, 4],
[4, 6]
];
const adjacencyList = {};
//여기서도 무방향, 방향인가에 따라 달라진다.
connections.forEach(([node1, node2]) => {
if (!adjacencyList[node1]) {
adjacencyList[node1] = [];
}
if (!adjacencyList[node2]) {
adjacencyList[node2] = [];
}
adjacencyList[node1].push(node2);
adjacencyList[node2].push(node1);
});
/*
adjacencyList = {
'1': [ 5, 2 ],
'5': [ 1, 2 ],
'2': [ 1, 5, 3 ],
'3': [ 2, 4 ],
'4': [ 3, 6 ],
'6': [ 4 ]
}
*/인접행렬은 특정 정점에 연결된 모든 정점을 자주 확인할때 유리하고 간선이 정점^2보다 훨씬 작을때 유리하다.
DFS를 재귀로
DFS는 BFS에서 큐 => 스택 으로 바꾸기만 하면 됐다.
저번 시간에 재귀도 배웠으니, 재귀로 한번 짜보자.
const graph = {
1: [2, 5],
2: [1, 5, 3],
3: [2, 4],
4: [3, 6],
5: [1, 2],
6: [4]
};
const visited = Array(n);
const dfs = (node, visited) => {
visited[node] = 1;
console.log("방문한 노드:", node);
// 현재 노드의 모든 이웃 노드에 대해 방문하지 않았다면 재귀 호출
for (let neighbor of graph[node]) {
if (!visited[neighbor]) {
dfs(neighbor, visited);
}
}
}
//dfs탐색 시작!
for(let node in gprah){
if(!visited[node]){
dfs(node, visited)
}
}
/*
결과:
1
2
3
4
6
5
*/참고로 비재귀DFS의 방문순서는 재귀DFS와 다르다..! 이점에 유의하여 DFS문제가 나오면 앞으론 재귀DFS만 사용하자.
트리
트리는 뭘까? 계층 구조를 가진 그래프의 일종이다. 즉, 무방향이면서 사이클이 없는 연결그래프다.
- 제일 꼭대기 정점을 root라고한다.
- 간선으로 직접 연결된 상-하 정점을 부모-자식 이라고함
- 자식이 없는 정점은 leaf다.
그래프의 일종이다!
트리의 BFS
루트에서 시작한다면 높이 순으로 방문하게 된다. => 큐를 이용하기 때문이다.
같은 높이에서 방문하는 순서는 정렬하는 기준에 따라 달라진다.
또한 visited배열이 필요하지 않다. => 부모를 제외한 인접 정점을 모두 큐에 넣으면 된다!
const adj = [...]; //길이는 10
const parentNum = Array(10);
const bfs = (root) => {
const queue = [];
queue.push(root);
while(q.length){
const cur = q.shift();
for(const next of adj[cur]){
if(parentNum[cur] === next) continue; //next가 cur의 부모인지 확인
q.push(next);
parentNum[next] = cur;
}
}
}트리의 DFS
const adj = [...];
const parentNum = Array(10);
const dfs = (cur) => {
for(const next of adj[cur]) {
if(parentNum[cur] === next) continue;
parentNum[next] = cur;
dfs(next);
}
}이진트리 순회
이진트리란? 각 정점의 자식이 최대 2개인 트리이다. 순회하는 방법은 총4개니 알아보자.
이진트리 저장
이진트리는 쉽게 저장할 수 있다. 각 정점의 자식이 최대 2개기때문에, 배열 하나로 처리할 수 있다.
/*
1
/ \
2 3
/ \ / \
4 5 6 7
\
8
*/
//없는 자리는 0으로 표현
const binaryTree = [1,2,3,4,5,6,7,0,0,0,8];
const leftChild = index * 2 + 1;
const rightChild = index * 2 + 2;배열 여러개로 처리하는 방법도 있다. 왼쪽-오른쪽 자식과 부모를 나눠서 저장한다.
/*
1
/ \
2 3
/ \ / \
4 5 6 7
\
8
*/
//같은 레벨의 자식을 때려넣는다!
const leftChildren = [2, 4, 6, 0, 0, 0, 0, 0];
const rightChildren = [3, 5, 7, 0, 8, 0, 0, 0];
const parents = [0, 1, 1, 2, 2, 3, 3, 5];이진트리 순회1) 레벨 순회
레벨(높이)순으로 방문한다. 뭔가 떠오르지 않는가?
const bfs = (root) => {
const q = [];
q.push(root);
while(q.length){
const cur = q.shift();
//현재 정점에 왼쪽, 오른쪽 자식이 존재하는지 체크하여 넣는다.
if(leftChildren[cur]) q.push(leftChildren[cur]);
if(rightChildren[cur]) q.push(rightChildren[cur]);
}
}이진트리 순회2) 전위 순회(preorder)
부모 => 왼쪽자식 => 오른쪽 자식순으로 방문한다.
즉 1,2,4,5,8,3,6,7순으로 방문한다. => DFS와 방문 순서가 동일하다.
const result = [];
const preorder = (cur) => {
result.push(cur);
if(leftChildren[cur]) preorder(leftChild[cur]);
if(leftChildren[cur]) preorder(rightChild[cur]);
}이진트리 순회2) 중위 순회(inorder)
왼쪽자식(존재하지 않을 때 까지) => 부모 => 오른쪽 자식 순으로 방문한다.
즉 4,2,5,8,1,6,3,7순으로 방문한다.
const result = [];
const preorder = (cur) => {
if(leftChildren[cur]) preorder(leftChild[cur]);
result.push(cur);
if(leftChildren[cur]) preorder(rightChild[cur]);
}이진트리 순회3) 후위 순회(postorder)
왼쪽자식(존재하지 않을 때 까지) => 오른쪽 자식 => 부모 순으로 방문한다.
즉 4,8,5,2,6,7,3,1순으로 방문한다.
const result = [];
const preorder = (cur) => {
if(leftChildren[cur]) preorder(leftChild[cur]);
if(leftChildren[cur]) preorder(rightChild[cur]);
result.push(cur);
}