안되면 외우자 3편 - 수학, 이분탐색, 투포인터

김영현·2024년 3월 20일

수학 순열 이분탐색 조합 코딩테스트 투포인터

안되면 외우자

목록 보기

3/9

수학

너무나 큰 정의긴한데, 어쨌든 수식을 세워서 풀 수 있는 종류이다.
예를들면 최소공배수, 최대공약수, 에라토스테네스의 체(소수 판별 알고리즘), 모듈러 연산 등!
따로 내릴 수 있는 정의는 없다.

예시 문제1) 소수 판별

소수란 1과 자기자신으로만 나뉘어지는 수 이다.
간단하게 구현하면 아래와 같다.

const isPrime = (n) => {
	if(n === 1) return false;
    for(let i = 2; i < n; i++){
      if(n % i === 0) return false;
    }
    return true;
}

O(n)짜리 코드인데, 유심히 관찰하면** O(√n)**에도 해결이 가능하다.

합성수N에서 1을 제외한 가장 작은약수를 x라고 하면...(n/x)또한 n의 약수다. 따라서 x <= (n/x)이다.
=> x <= √n

const isPrime = (n) => {
	if(n === 1) return false;
    for(let i = 2; i*i <= n; i++){
      if(n % i === 0) return false;
    }
    return true;
}

하나의 수 판별은 이렇게 됐다.

하지만 범위 내 소수의 판별은 어떻게 할까?
단순하게 for문을 돌려 위 수식을 적용하면 O(n√n)이 된다.(실제론 조금 더 빠르다).
여기서 더 최적화를 해보자.

소수의 배수는 무조건 소수가 아니다. 따라서 범위에서 탈락시킨다.
범위에서 탈락한 소수는 배수를 탈락시킬 일이 없다.

//1~n까지 소수
const eratos = (n) => {
    const primeArr = Array(n+1).fill(1);
    const result = [];
    primeArr[1] = 0;
	for(let i = 2; i * i <= n; i++){
    	if(!primeArr[i]) continue;
    	for(let j = i*i; j<=n; j+=i){
        	primeArr[j] = 0;
    	}
    }
    primeArr.forEach((prime,i) => prime && result.push(i));
    return result;
}

시간복잡는다 O(n log(logn))이다 O(n)하고 비슷함!

예시 문제2) 최대 공약수, 최소 공배수

이는 재귀를 활용해서 구할 수 있다.
최대 공약수의 정의는 다음과 같다.

두 수를 나누어 떨어지게 하는 수중 가장 큰 공통 수.
두 수 A,B에 대해서 A%B = r이라고 하면, GCD(A,B) === GCD(B,r)이다.

const gcd = (a,b) => {
  if(a === 0) return b;
  return gcd(b%a, a);
}

최소 공배수는 A*B / gcd(a,b)다.

const lcm = (a,b) => a*b / gcd(a,b);

예시 문제3) 조합, 순열

이분 탐색

이분탐색은 정렬이 선행되어야한다. 즉, 자연수거나, 시간이거나, 낮음~높음 등이 전제되어있다면 이분탐색이 가능하다.

예시문제1) 세 수의 합

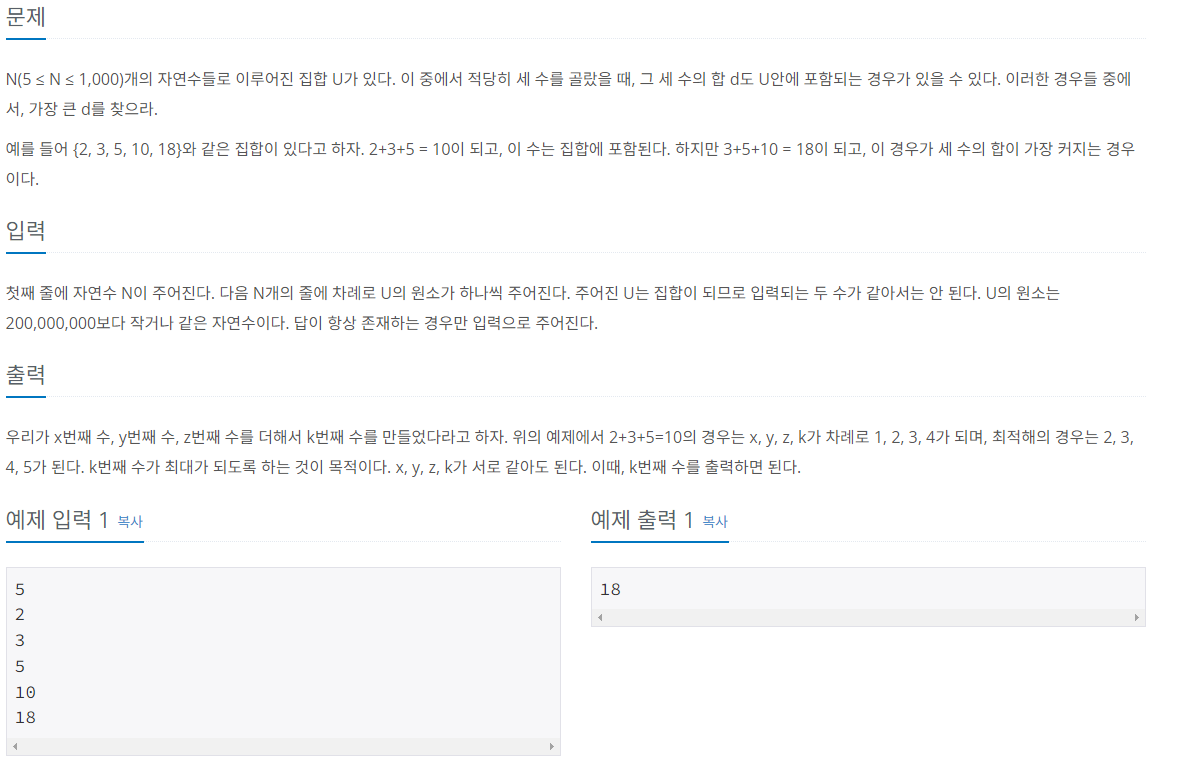
핵심은 이분 탐색을 어떻게 활용하느냐다.

두 수의 합경우의 수를 모조리 더한다.
두 수의 합 + 남은 한 수 값을 U 내부에서 이분탐색 한다.

// const n = 5;
// const input = [3,2,3,5,10,18];

const twoSum = [];

for(let i = 0; i < n; i++){
	for(let j = i; j < n; j++){
    	twoSum.push(input[i] + input[j]);
    }
}

twoSum.sort((a,b) => a-b);

//이분탐색

예시문제2) paramertric serach(랜선 자르기)

파라메트릭서치는 문제가아니라, 문제의 종류다.
최적화 문제(최솟값, 최댓값 등을 구해야함)를 결정 문제로 바꾸어 푸는 방법이다. (사실 이렇게 이분탐색 나오는 경우가 많을듯?)

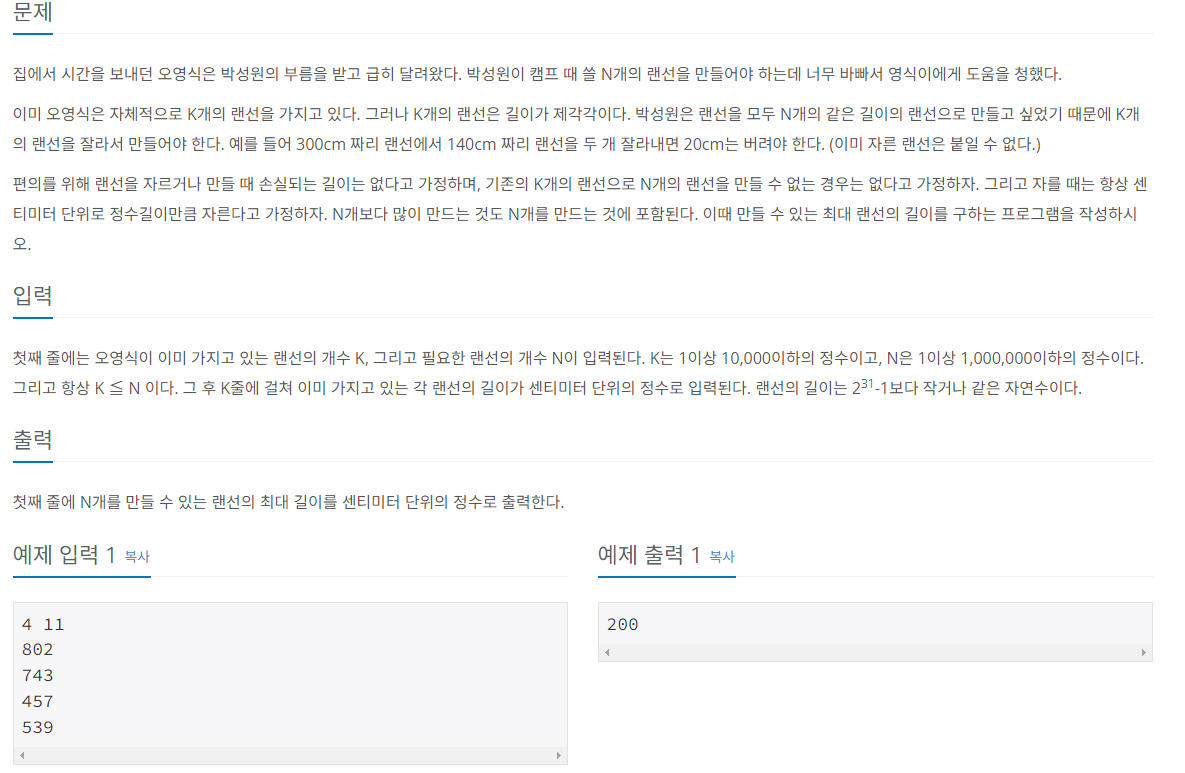
이 문제는 N개를 만들 수 있는 최대길이를 구해야한다. (최적화 문제)
이를 랜선의 길이가 X일때 랜선이 N개 이상인가? (결정문제)로 바꾸어 풀면, 놀랍게도 이분탐색이 가능하다.

//const [k, n] = [4,11];
//const arr = [802, 743, 457, 539];

const caculate = (x) => {
	let cur = 0;
    //가지고있는 랜선 길이를 순회하며 x(파라미터로 받은 랜선의 길이)로 나눔. 그 값음 cur에 누적함.
    for(let i = 0; i< k; i++) {
    	cur += arr[i]; / x
    }
    //랜선의 길이를 x로 나누어 더한 값이 n보다 큰지 확인
    return cur >= n;
}

let start = 1;
let end = 2**31 - 1; //최대길이

while(start < end){
	let mid = (start+end+1)/2;
  
    //cur이 n보다 같거나 크면, 길이에 여유가 있으므로 나누는 길이를 키워본다.
  	if(calculate(mid)) {
    	start = mid;
    } else {
    //cur이 n보다 작으면, 길이에 여유가 없으므로 나누는 길이를 줄여본다.
      end = mid - 1;
    }
}

return start

투 포인터

2중for문으로 O(n^2)이 걸리던 걸 O(n)으로 풀 수 있게하는 기법.
C언어의 포인터는 아니고 커서라고 생각하면 편하다.

투 포인터는 결국 이분탐색으로도 풀 수 있다. 시간복잡도는O(n)에서 O(n log n)으로 증가함.
while문 예외사항이 굉장히 중요하다.

예시문제) 부분합

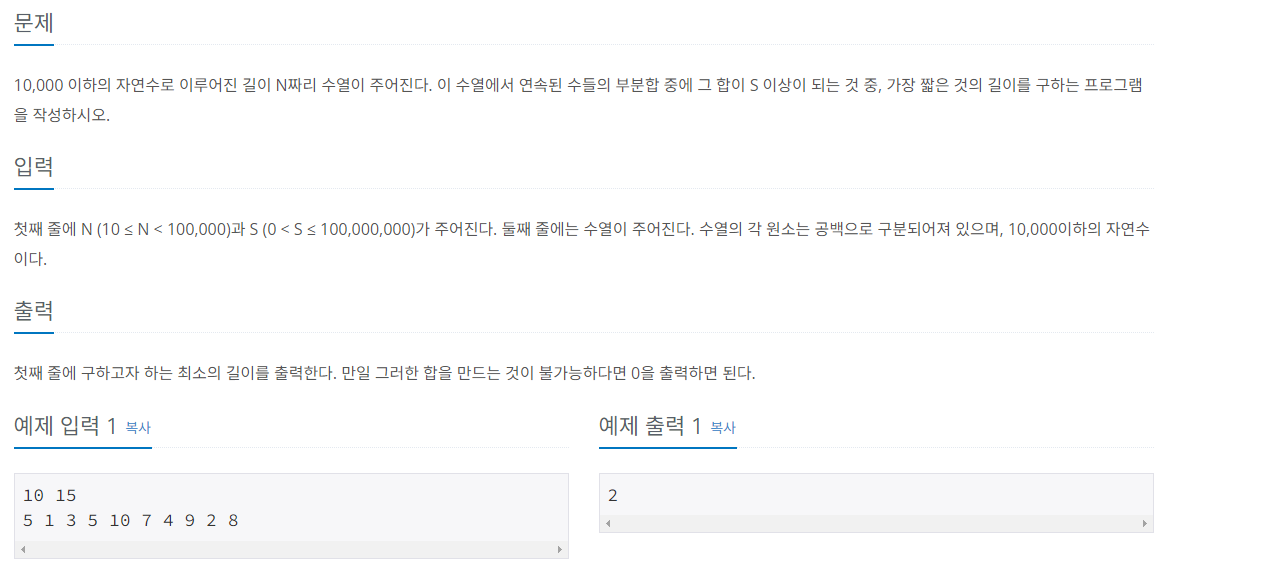
생각해본 풀이는 다음과 같다.

최초 지점부터 end커서를 움직이며 합을 구한다.
만약 합이 S이상이라면, 거리를 기록하고 이전값을 뺀다.
반복한다...!

//const [N,S] = [10,15];
//const arr = [5,1,3,5,10,7,4,9,2,8];

let total = arr[0];

let end = 0;
let min = n+1;

for(let st = 0; st < n; st++){
	while(end < n && total < s){
    	end++;
        if(end !== n){
        	total += arr[end];
        }
    }
    if(end === n) break;
    min = Math.min(min, end - start + 1);
    total -= arr[start];
}

//예외사항!
if(min === n) min = 0;
return min;