안되면 외우자 2편 - 백트래킹, dp, 그리디

김영현·2024년 3월 19일

DFS DP 그리디 백트래킹 안되면 외우자 재귀

안되면 외우자

목록 보기

2/9

안되면 외우자

제일 약한 파트 3가지 백트래킹,dp,그리디에 대해 알아보자!

백트래킹

현재 상태에서 가능한 모든 후보군을 따라들어가며 탐색

정의는 이렇다. 생각나는대로 일단 정의해보자.

재귀를 이용한다. 특히 DFS를 이용한다. => 인접한 방향(노드)부터 탐색해 나간다.
- DFS를 이용한다면, 스택을 이용할 수도 있지 않을까? => 재귀로 구현할때 보다 코드가 훨씬 길어진다.
각 예외사항이 정말로 중요하다. 이를 가지치기(아닌 경우는 재귀를 빠르게 종료)하는게 백트래킹이다.

예시문제) N-Queen

n x n 체스판 위에 n개의 퀸을 서로 공격할 수 없게 놓을 수 있는 경우의 수

어떻게 구할지 천천히 생각해보자. (4x4라고 일단 생각)

퀸을 특정 좌표에 놓으면 같은 행,열,대각선에는 퀸을 놓지 못한다. 이때 (0,1)에 두었다고 가정해보자.
같은 열(0 + 1~3,0), 같은 행(0,0 + 1~3), 대각(0 + 1~3,y + 1~3)에는 퀸을 놓지 못한다. 따라서 제일 가까운 좌표중 하나인 (1,3)에 둘 수 있음.
(1,3)에 퀸을 둔다면, 그다음 좌표인 (2,y)에는 둘 공간이 없다. 따라서 다시 (0,1)에 두었던 상태로 돌아감.
(1,4)에 퀸을 둔다면, 그 다음 좌표중 (2,2)에 둘 수 있다.
(2,2)에 퀸을 둔다면, 그 다음 좌표중 (3,y)에는 둘 수 있는 공간이 없다. 다시 되돌아간다. 위에서 이미 모든(1~3행)좌표를 탐색했으므로, (0,2)에 퀸을 놓아본다.

...모든 체스판 좌표에 퀸을 한번씩 놓아본다.

let cnt = 0;

const column = Array(n);
const leftBotToRightTop = Array(n*2 -1);
const leftTopToRightBot = Array(n*2 -1);

const queen = (j) => {
	if(n === j){
      cnt++;
      return;
    }
    for(let i = 0; i<n; i++){
        //같은 열, 좌하단에서 우상단으로 가는 대각선, 좌상단에서 우하단으로 가는 대각선에 퀸이 존재하는지 체크!
      	if(column[i] || leftBotToRightTop[i + j] || leftTopTopRightBot[i - j + n -1]) continue;
        column[i] = 1;
        leftBotToRightTop[i + j] = 0;
        leftTopTopRightBot[i - j + n -1] = 1;
      
        queen(j+1);
      
        column[i] = 0;
        leftBotToRightTop[i + j] = 0;
        leftTopTopRightBot[i - j + n -1] = 0;
    }
}

백트래킹의 핵심은 가지치기다. 어떤 조건을 탐색하지 않을 지가 핵심이다.
따라서 위의 경우 열, 대각선2개를 어떻게 방문처리 할 건지가 핵심이었다.
상태 공간 트리를 만드는 건 부차적일 뿐이다.

DP

DynamicProgramming. 실제 뜻과는 많이 다르다. Dynamic이라는 이름이 멋있어보여서 그렇게 제출했다나 뭐라나...?
아무튼 정의로 들어가보자.

*하위 문제를 먼저 푼 후 결과를 쌓아올려 주어진 문제를 해결함.

혼자 생각해본 정의는 이렇다.

이전 값을 이용해서 푸는 기법이다. 핵심은 이전 값을 현재 값과 비교하는 방식이다.(점화식)
두가지 방식으로 풀 수 있다. top-down, bottom-up. 보통 풀던 방식인 dp[1], dp[2]등 초기값을 넣고 계산하는 방식이 bottom-up이다. top-down은 재귀적으로 푼다는데, 해본적이 없다.

결국 점화식을 찾아낸 후, 첫 항 부터 천천히 찾아내면 된다. <<< 이게 제일 어려움...😫

예시문제) 1로 만들기 2

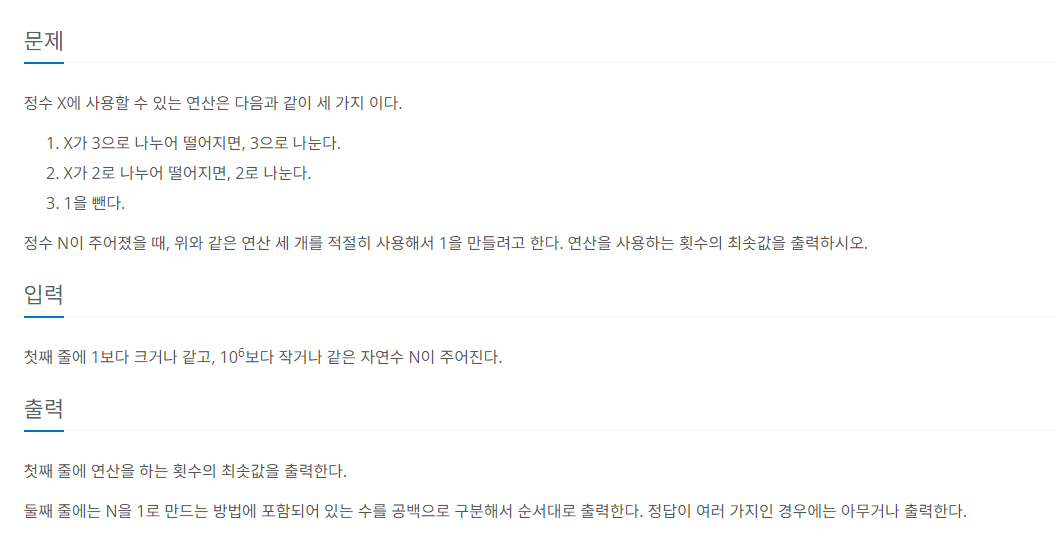
dp로 푸는 문제면서, 과정을 기록해야한다.
다시말해 새로운 배열이 필요함.

//dp[i]는 i를 만드는 최소한의 연산 횟수
const dp  = Array(10**6 + 1);
const pre = Array(10**6 + 1);

dp[1] = 0;

for(let i = 2; i <= n; i++){
	dp[i] = dp[i-1] + 1;
    pre[i] = i - 1; //정수 i가 i-1번째 정수에서 연산(+1)을 했다.
    
    //i가 2로 나누어 떨어지며, dp[i]의 연산횟수가 dp[i/2] + 1보다 클때
    if(i%2 === 0 && dp[i] > dp[i/2] + 1){
      dp[i] = dp[i/2] + 1;
      pre[i] = i/2; //정수 i가 i/2 번째 정수에서 연산(*2)을 했다.
    }
    
    //2나 3으로 나눠지는경우 3으로 나눠질때가 더 최솟값이므로 아래에서 if문을 걸어준다.
    if(i%3 === 0 && dp[i] > dp[i/3] + 1){
      dp[i] = dp[i/3] + 1;
      pre[i] = i/3 //정수i가 i/3번째 정수에서 연산(*3)을 했다.
    }
}

let cur = n;
const result = [];

//경로배열은 값이 곧 인덱스라서 이렇게 넣어줍니다.
while(cur !== 1){
  result.push(cur);
  cur = pre[cur];
}