개념과 구현을 함께 배우는 선형대수학 🙌

스칼라의 집합이다.행렬을 구성하는 기본단위 이다. 크기만 나타내는 스칼라와 달리 벡커는 크기와 방향을 모두 나타태는 개념이다. 데이터가 가로 방향인 행을 행 벡터라고 볼수 있고,세로 방향인 열을 열 벡터라고 한다. 특정하지 않는 경우에는 기본적으로 열벡터를 의미한다.

행렬의 모양이나 구조에 따라 여러가지 종류가 존재한다 (다음 포스팅에 더 자세히 올릴께요!) 벡터의 집합이다. \- 열 벡터의 집합이라고 생각할 수 있고, 행 벡터의 집합이라고도 생각할 수 있다. 스칼라는 스칼라 끼리, 벡터는 다른 벡터와 연산이 가능하듯이 행렬간의

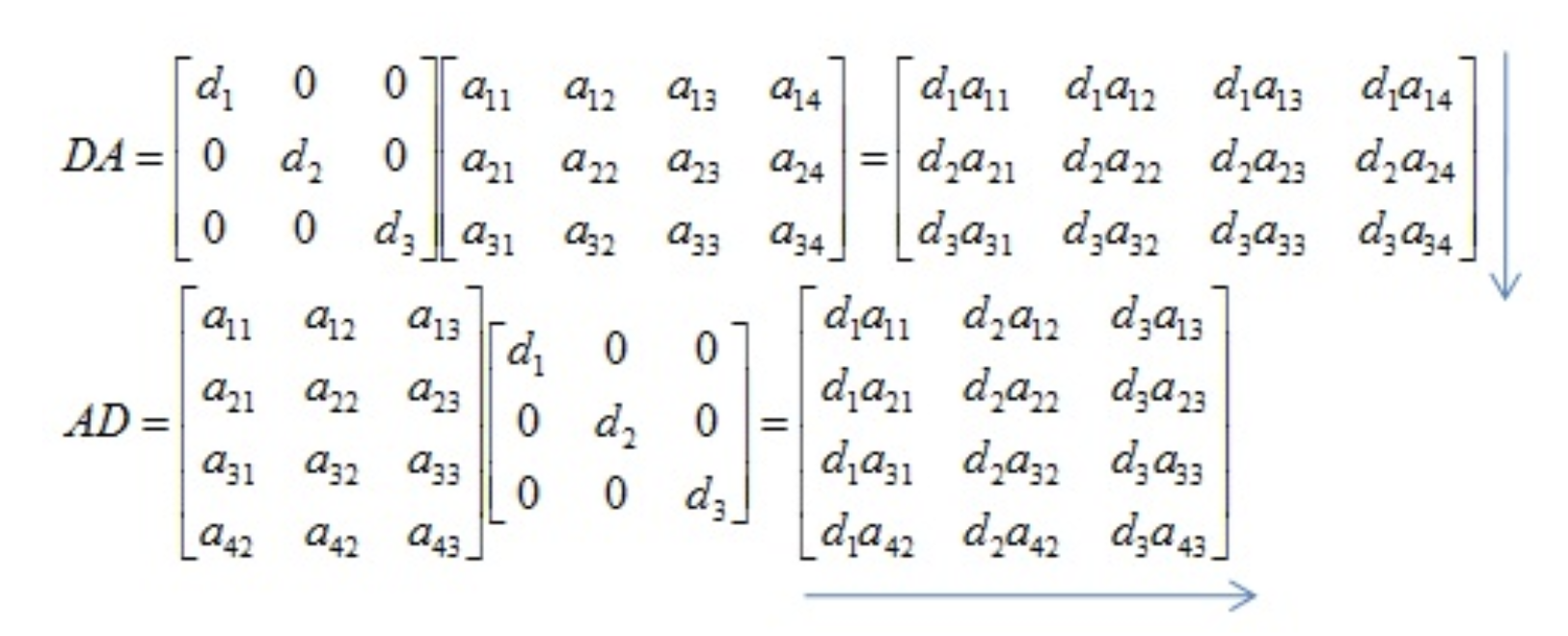
전치 행렬은 원래 행렬의 행과 열을 뒤바꾼 행렬을 말합니다. 즉, 주어진 행렬 A의 (i, j)번째 원소는 전치 행렬인 $A^T$의 (j, i)번째 원소가 됩니다. 주어진 행렬 A의 전치 행렬은 $A^T$ 로 표기합니다.원래 행렬 A:$$A = \\begin{pmatr

선형 방정식은 한 개 이상의 변수와 이 변수들의 계수로 이루어진 일차식으로, 다음과 같은 일반적인 형태를 가지는 방정식을 말합니다: $a_1x_1 + a_2x_2 + \\ldots + a_nx_n = b$여기서 $a_1$, $a_2$, $a_n$은 계수이며, $x_1$

역행렬은 선형 대수학에서 중요한 개념으로, 주어진 정사각 행렬 A에 대해 A의 역행렬을 A⁻¹로 표기하며, 다음 조건을 만족하는 행렬입니다:A와 A⁻¹의 곱은 단위행렬(I)이 된다: $A^{-1} A = A A^{-1} = I$역행렬은 유일하게 존재한다: A의 역행

집합에 있는 두 원소를 더했을때 해당 집합에 속한다.한 원소를 상수배 했을때 해당 집합에 속한다. 위의 두가지 조건을 만족한다면 해당 집합을 "공간(Space)"이라고 부를 수 있습니다. 위 조건을 만족하는 공간이 아래의 조건(공리)를 만족한다면 "벡터공간 (Vecto

반면에 선형 종속한 벡터들은, 적어도 하나의 벡터가 나머지 벡터들의 선형 조합으로 나타내지는 것을 의미합니다. 즉, 어떤 벡터가 다른 벡터들의 선형 조합으로 만들어질 수 있다면, 이 벡터들은 선형 종속입니다. 수식적으로는 다음과 같이 표현됩니다.벡터들 v₁, v₂, .

기저(Basis)는 벡터 공간(Vector Space) 내의 벡터들로 이루어진 집합으로, 이 벡터들이 선형 독립이면서 그 벡터 공간 내의 모든 벡터를 생성할 수 있는 최소한의 벡터들을 말합니다. 다시 말해, 기저는 벡터 공간 내의 모든 벡터를 어떤 조합으로도 나타낼 수