[선형대수학] 파이썬으로 배우는 행렬 종류

📌 전치 행렬

전치 행렬은 원래 행렬의 행과 열을 뒤바꾼 행렬을 말합니다. 즉, 주어진 행렬 A의 (i, j)번째 원소는 전치 행렬인 $A^T$의 (j, i)번째 원소가 됩니다. 주어진 행렬 A의 전치 행렬은 $A^T$ 로 표기합니다.

원래 행렬 A:

전치 행렬 $A^T$:

Numpy로 해보는 전치행렬

import numpy as np 
A = np.array([[1,2],[3,4],[5,6]])
At = np.transpose(A)

print(At)
#[[1,3,5]
 [2,4,6]]

Numpy로 해보는 전치행렬(간단한 방법)

import numpy as np 
A = np.array([[1,2],[3,4],[5,6]])
At = A.T

print(At)
#[[1,3,5]
 [2,4,6]]

📌 대칭 행렬

대칭 행렬은 주 대각선을 기준으로 대칭되는 원소들이 같은 값을 가지는 행렬입니다. 즉, A의 (i, j)번째 원소와 (j, i)번째 원소가 같습니다.
주어진 대칭 행렬 A는 A = $A^T$로 표현합니다.

대칭 행렬은 몇가지 특징을 가집니다:

• 대칭 행렬 두개가 존재 할때 행렬간의 덧셈과 뺄셈의 결과 또한 대칭 행렬이 됩니다.

  $A = \begin{pmatrix} 8 & 2 \\ 2 & 4 \\ \end{pmatrix}$
  $B = \begin{pmatrix} 3 & 1 \\ 1 & 2 \\ \end{pmatrix}$

• 행렬 A가 대칭 행렬일때 제곱을 취했을때도 대칭 행렬입니다.
  $A = \begin{pmatrix} 8 & 2 \\ 2 & 4 \\ \end{pmatrix}$
  $A^2 = \begin{pmatrix} 64 & 4 \\ 4 & 16 \\ \end{pmatrix}$
• 기존 행렬 A와 자신의 전치 행렬 $A^T$를 곱합 형태인 $AA^T$ 또는 $A^TA$는 대칭 행렬 형태입니다.

Numpy로 해보는 대칭행렬

import numpy as np 
A = np.array([[1,0,2],[0,2,1],[2,1,1]])
At = A.T

A == At
#array([[True, True, True],
		[True, True, True],
        [True, True, True]])

Numpy로 해보는 대칭행렬

import numpy as np 
A = np.array([[1,0,2],[0,2,1],[2,1,1]])
At = A.T

print(np.matmul(A, At))
#[[5 2 4]
 [2 5 3]
 [4 3 6]]

📌 대각 행렬

대각 행렬은 주 대각선을 제외한 모든 원소가 0인 행렬입니다. 대각 행렬은 주로 스케일 변환을 나타내는 데 사용됩니다.
대각 행렬 D는 대각성분들을 D = diag(d1, d2, ..., dn)로 표기합니다.

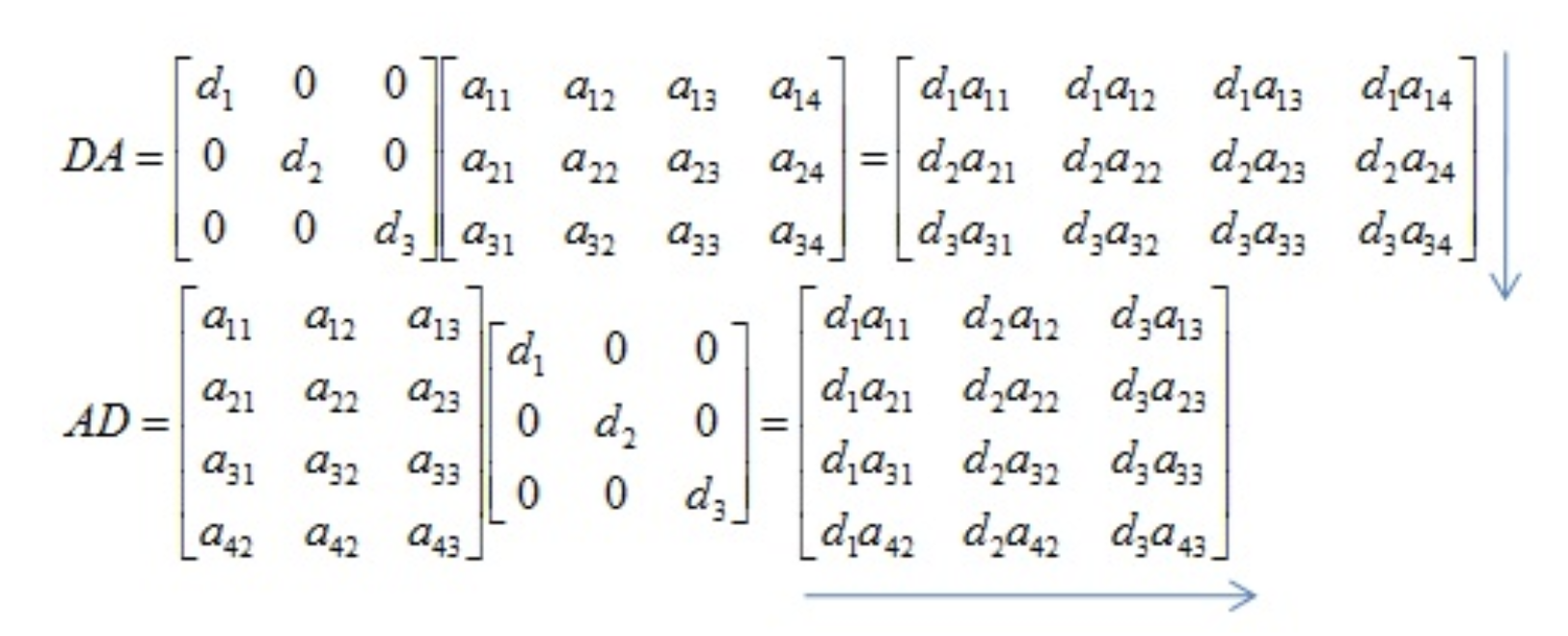
• 대각 행렬을 오른쪽에 곱하는 경우 기존 행렬의 열값이 대각 원소의 배수가 됨
• 대각 행렬을 왼쪽에 곱하는 경우 기존 행렬의 행 값이 대각 원소의 배수가 됨

Numpy로 해보는 대각행렬

import numpy as np 
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
D = np.diag([1,5,9])   #대각행렬 생성 함수

print(D)
# [[1 0 0]
  [0 5 0]
  [0 0 9]]

AD = np.matmul(A,D)
print(AD)
#[[1,10,27]
  [4,25,54]
  [7,40,81]]

📌 단위 행렬

단위 행렬은 주 대각선의 모든 원소가 1이고, 나머지 원소가 0인 정사각 행렬입니다. 단위 행렬은 행렬 곱셈에서의 항등원 역할을 합니다.
n x n 크기의 단위 행렬은 I 또는 I_n으로 표기합니다.

Numpy로 해보는 단위행렬

import numpy as np 
A = np.array([[1,2,3],[4,5,6],[7,8,9]])
I = np.identity(3)

print(I)
# [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

AI = np.matmul(A,I)
print(AI)
#[[1. 2. 3.]
 [4. 5. 6.]
 [7. 8. 9.]]