행렬이란?
- 행렬의 모양이나 구조에 따라 여러가지 종류가 존재한다 (다음 포스팅에 더 자세히 올릴께요!)
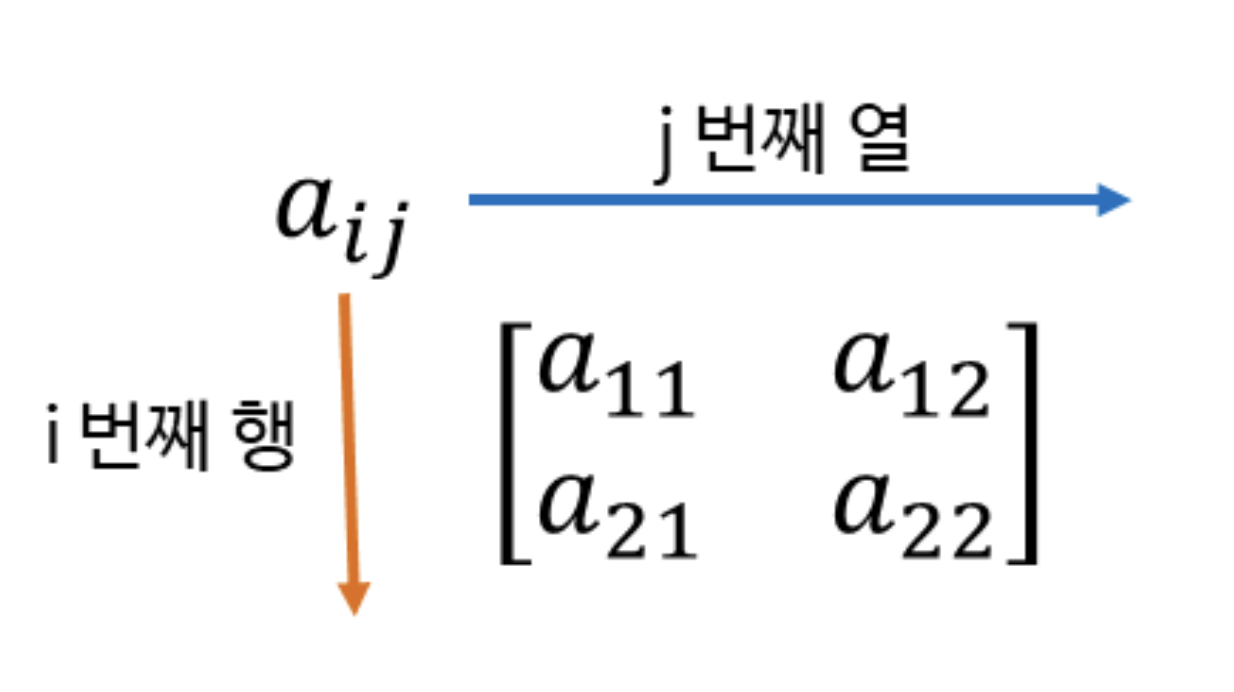
- 벡터의 집합이다.
- 열 벡터의 집합이라고 생각할 수 있고, 행 벡터의 집합이라고도 생각할 수 있다.
행렬의 덧셈과 뺄셈
스칼라는 스칼라 끼리, 벡터는 다른 벡터와 연산이 가능하듯이 행렬간의 덧셈, 뺄셈도 가능합니다. 각 행렬의 같은 위치에 대응하는 원소끼리 덧셈, 뺄셈을 함으로써 연산을 수행할 수 있습니다.
(Tip) 같은 위치란 연산하고자 하는 두 원소의 행과 열번호가 동일하다는 것을 의미합니다.
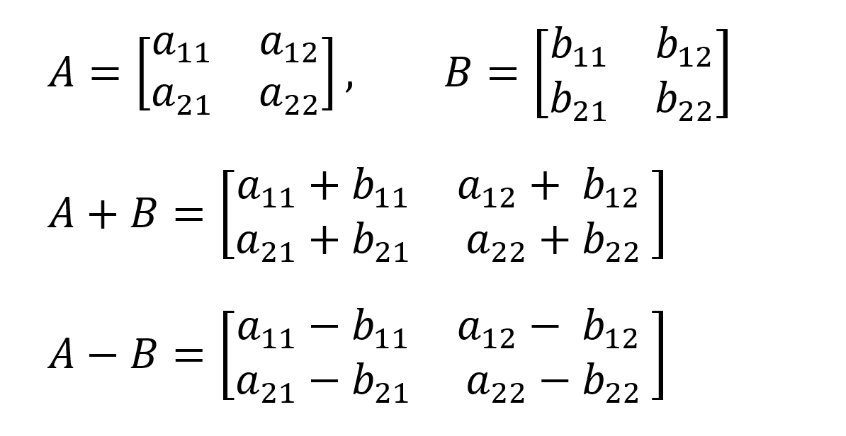
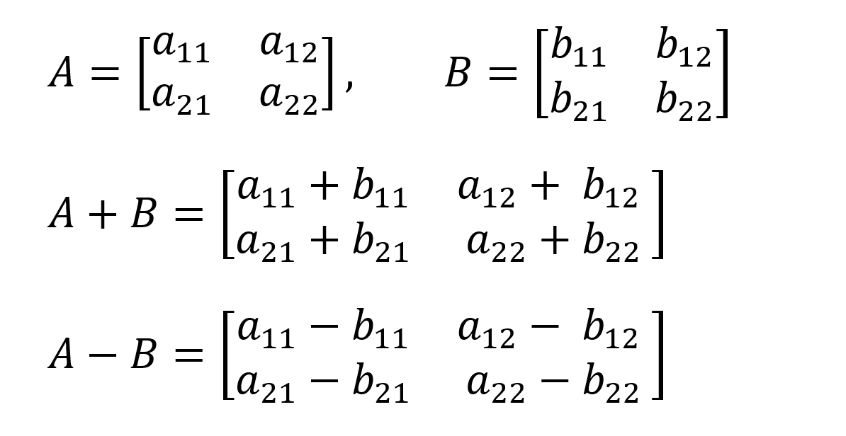
Numpy로 해보는 행렬 덧셈
import numpy as np
A = np.array([[1,2],[3,4],[5,6]])
B = np.array([[7,8],[9,10],[11,12]])
C = A+B
print(C)
# [[8,10],
[12,14],
[16,18]]Numpy로 해보는 행렬 뺄셈
import numpy as np
A = np.array([[7,8],[9,10],[11,12]])
B = np.array([[1,2],[3,4],[5,6]])
C = A+B
print(C)
# [[6,6],
[6,6],
[6,6]]행렬의 스칼라 곱
행렬에 실수 A를 곱하는 연산으로, 행렬의 각 원소마다 실수 A값을 곱하게 됩니다. 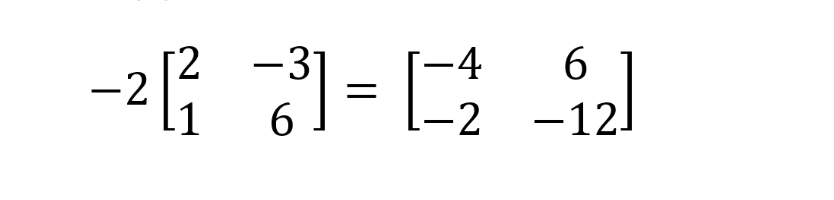
스칼라의 곱의 기하학적 의미는 이전 포스팅에서도 말씀드렸듯이, 실수 A값에 따라 행렬내 벡터의 길이가 달라지게 됩니다.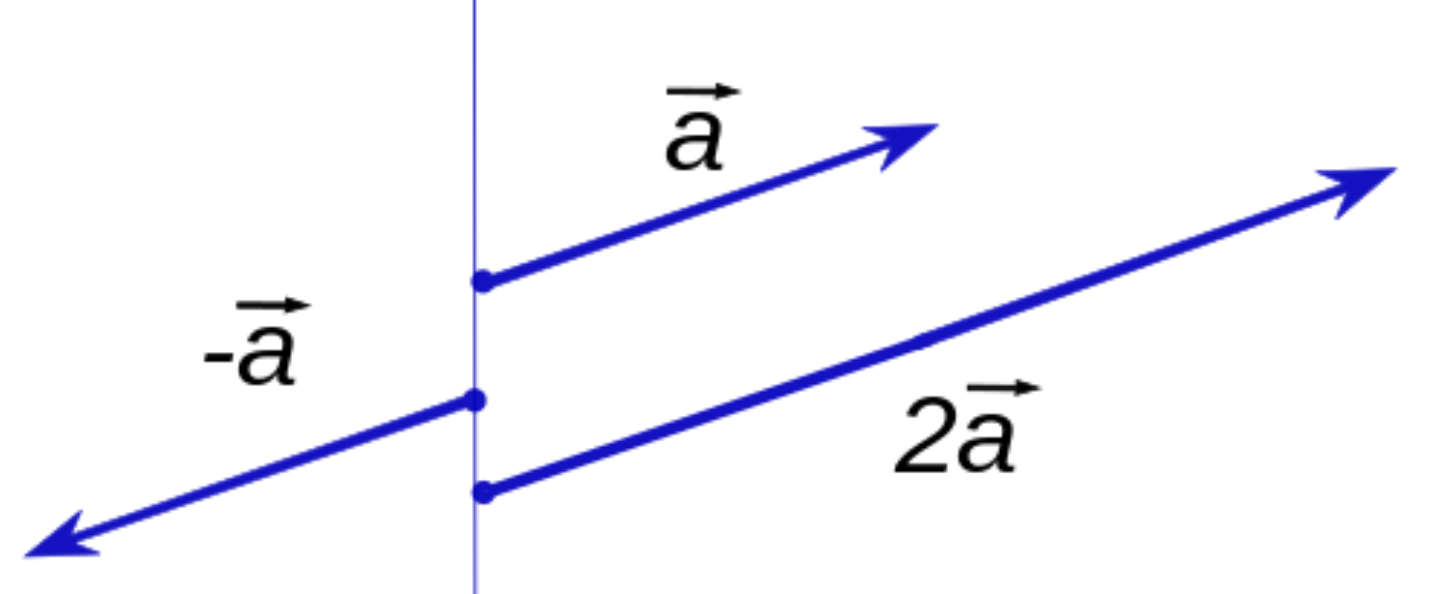
Numpy로 해보는 행렬 스칼라곱
import numpy as np
A = np.array([[1,2],[3,4],[5,6]])
b = 2
C= b*A
print(C)
# [[2,4],
[6,8],
[10,12]]행렬 원소의 곱
행렬 원소의 곱은 행렬의 곱과는 다르니 유의해야합니다. 행렬의 원소의 곱은 덧셈과 뺄셈의 연산자 처럼 동일한 위치에 있는 원소끼리를 곱한 값으로 인해 나오게 됩니다.
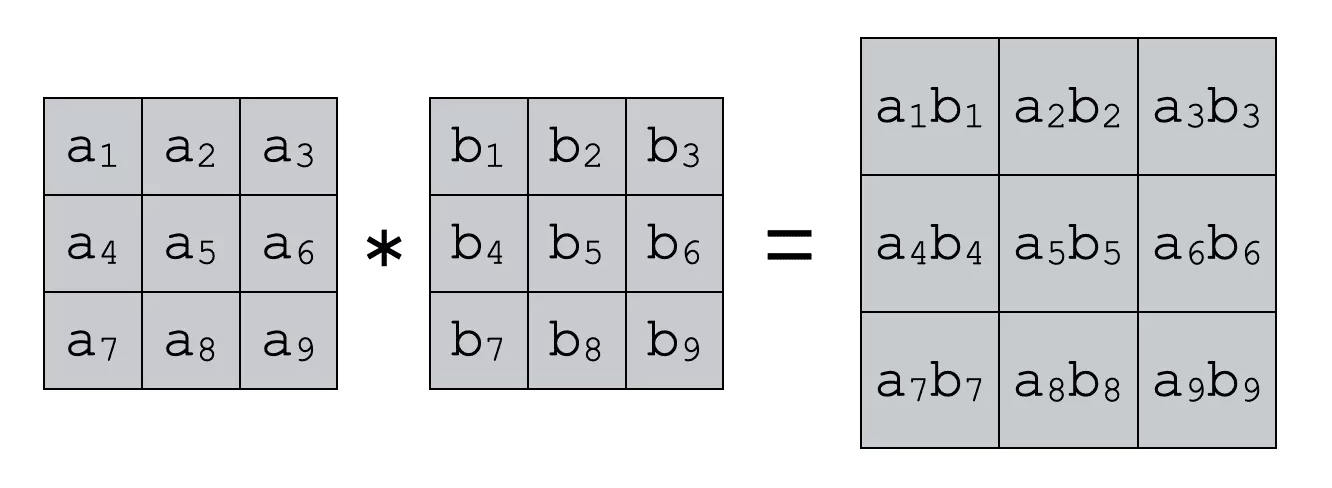
Numpy로 해보는 행렬 원소의 곱
import numpy as np
A = np.array([[1,2],[3,4],[5,6]])
B = np.array([[7,8],[9,10],[11,12]])
C = np.multiply(A,B)
print(C)
# [[7,16],
[27,40],
[55,72]]행렬의 곱
행렬곱은 행렬끼리 서로 곱하는 것을 의미하지만 일반적인 곱셈처럼 아무 때나 계산할 수 있는 것이 아니라 정해진 조건에 부합해야 합니다. 그 조건은 바로 앞에 있는 행렬의 열크기와 뒤의 행렬의 행 크기가 일치해야 하는 것입니다.
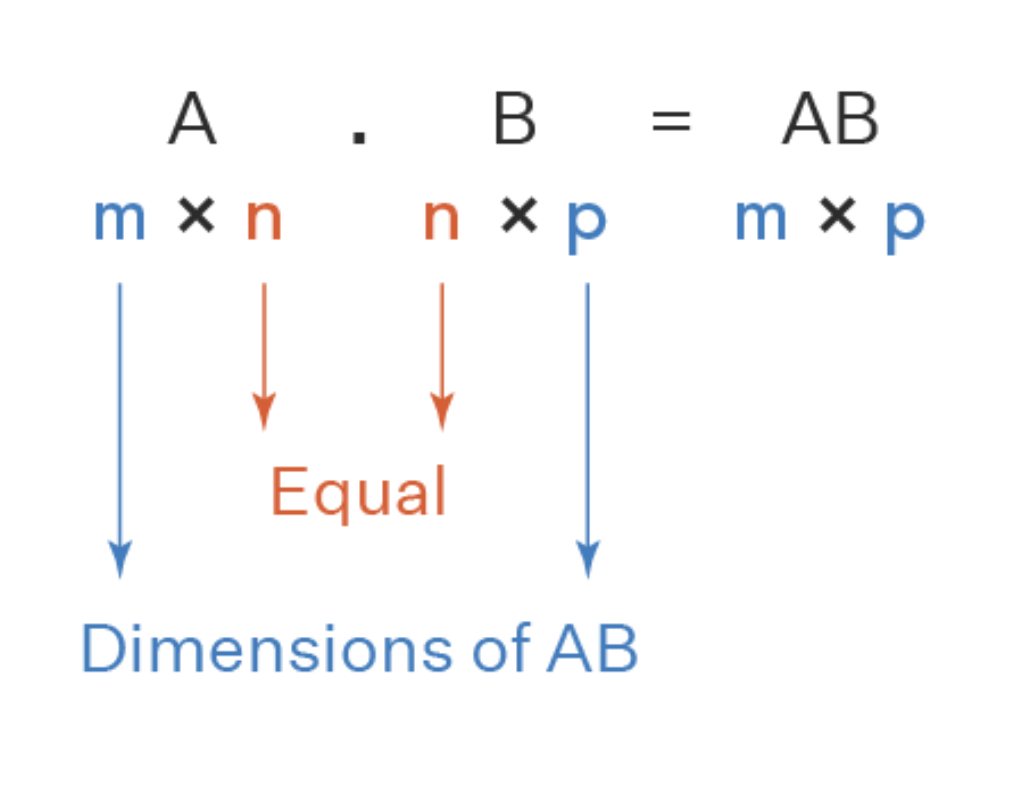
또다른 특이한 점이 있다면 교환법칙이 적용되지 않는다는 점입니다. 곱셈,덧셈에서는 53, 35는 교환법칙에 의해 동일한 결과값을 가져옵니다. 하지만 행렬의 곱셈에서는 가능하지 않습니다. 쉽게말해 일반적으로 AB 와 BA 는 같지 않습니다. 다음으로 설명할 행렬 곱의 작동 방식을 이해하시면 왜 교환법칙이 적용이 되지 않는지를 이해할 수 있습니다.
쉬운 이해를 위해 예시를 가지고 설명하도록 하겠습니다.
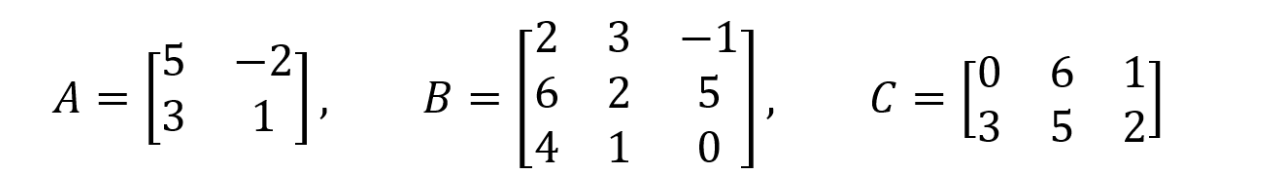
위에서도 말씀드렸듯이 행렬의 곱을 가능케하는 조건은 두 행렬의 행,열의 크기 같은것 끼리 가능한 것입니다! 그렇다면 A의 행은 2 B의 열은 3이니 곱이 불가능한 조합입니다.
그러면 A와 C는 어떠한가요? 가능한 조합입니다!! A와 C 행렬 곱의 작동 방식은 아래와 같습니다.
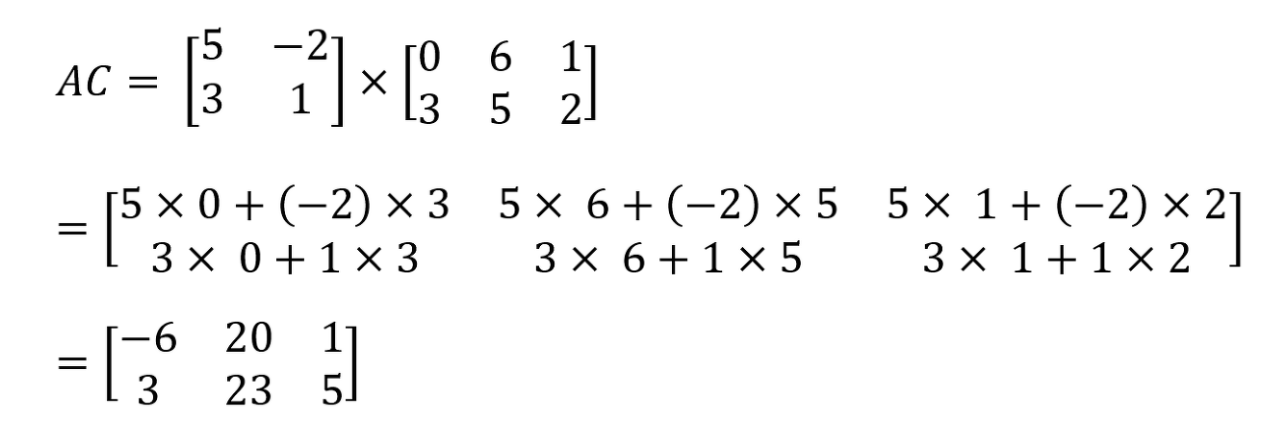
곱의 과정을 보면 쉽게 행렬의 곱셈에서 교환법칙이 이루어질 수 없음을 알 수 있습니다. 두 행렬의 순서가 바뀌게 된다면 행과 열의 크기가 맞지않아 행렬 곱을 수행할 수 없거나, 또는 전혀 다른 결과값을 도출하게 됩니다.
Numpy로 해보는 행렬 곱
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[7, 8], [9, 10], [11, 12]])
C = np.matmul(A, B)
print(C)
# [[ 58 64]
[139 154]]
#@ 기호를 사용할 수 있음
import numpy as np
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[7, 8], [9, 10], [11, 12]])
C = A @ B
print(C)
# [[ 58 64]
[139 154]]