Node 03. 시계열 데이터 EDA

3-1. 들어가며

---

학습 목표

• 시계열 데이터 표현: 그래프 그리기
• 시계열 특화 EDA: ACF Plot, PACF Plot

3-2. 시각화를 통한 시계열 데이터 탐색

---

용어 정리

• EuStockMarkets 데이터셋
  • 독일 주가 지수(DAX), 스위스 주가 지수(SMI), 프랑스 주가 지수(CAC), 영국 주가 지수(FTSE) 포함

시계열 데이터 그래프

• Line plot

  • 데이터 시간 및 순서에 따라 표현
  • 시계열 형태 및 변화를 쉽게 포착할 수 있음
    

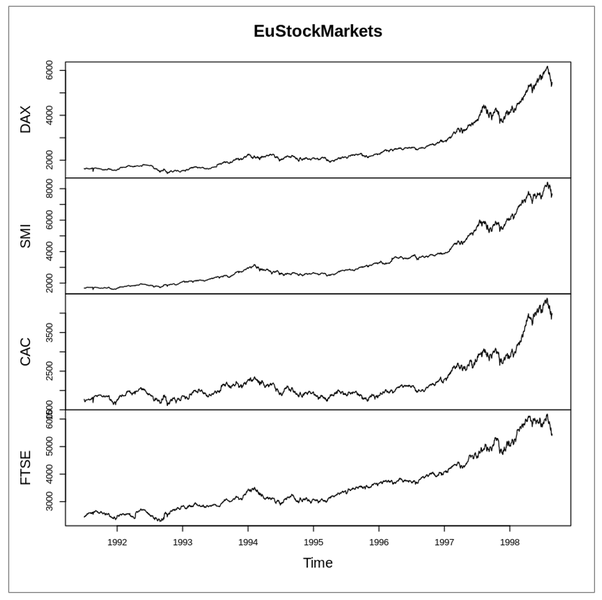
• Histogram

  • 변수에 대한 구간별 빈도수
  • 가로축 : 변수 구간
  • 세로축 : 도수
  • 막대는 서로 안겹치는 특징
  • 시계열 데이터에서는 1차 차분에 대해 히스토그램을 그리면 특정 분포 관찰 가능!
    

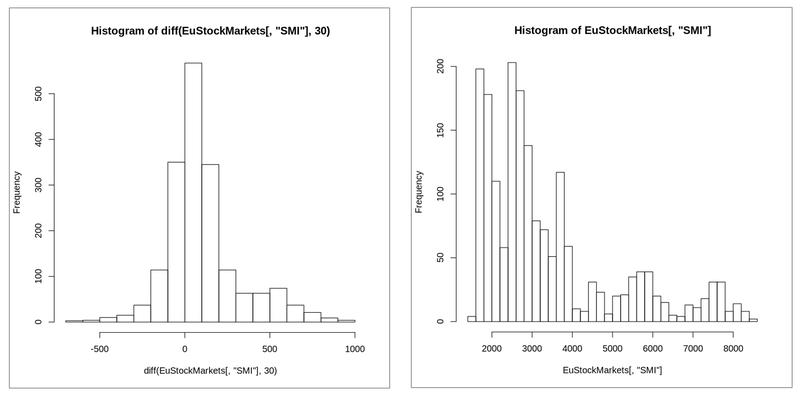
• Scatter plot(산점도)

  • 좌표 x, y를 활용
  • x와 y가 만나는 지점을 시각화
  • 두 시계열 관계에 대한 유의미한 정보 확인
  • 데이터 차분으로 새로운 의미를 찾을 수도 있음!
    

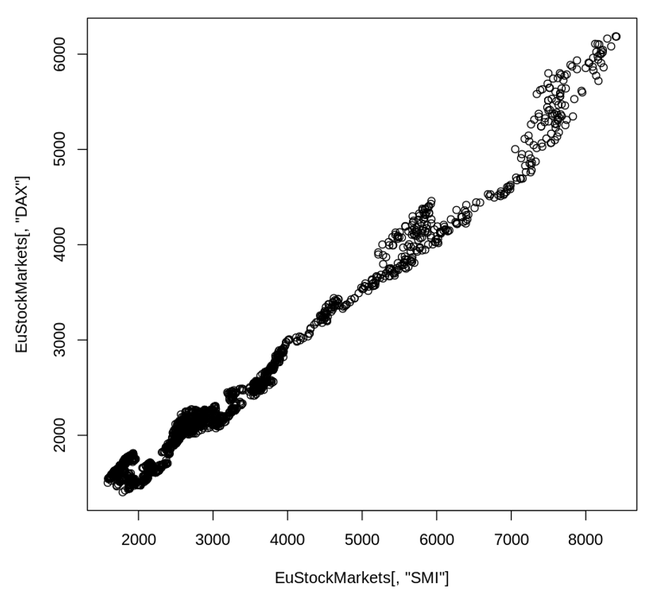
• Circular Chart

  • scatter plot 응용
  • 계절성 시각화 시 유용(그러나 보통, 시계열 데이터의 유의미한 인사이트를 얻기는 어려운 형태)
    

eustockmarkets 데이터셋으로 실습

• DAX 컬럼의 plot 그리기

plt.figure(figsize = (5,10))
plt.subplot(4,1,1)

plt.plot(eustockmarkets['DAX'])
plt.subplot(4,1,2)

plt.plot(eustockmarkets['SMI'])
plt.subplot(4,1,3)

plt.plot(eustockmarkets['CAC'])
plt.subplot(4,1,4)

plt.plot(eustockmarkets['FTSE'])

plt.show()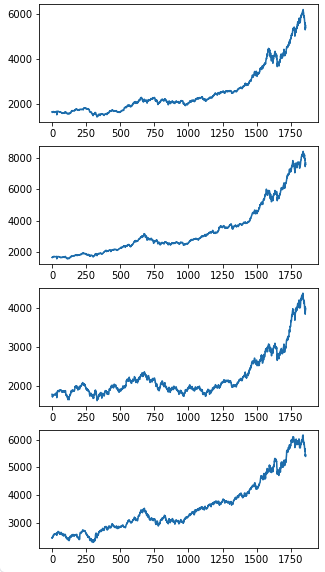

• DAX 컬럼 히스토그램 생성

plt.hist(eustockmarkets['SMI'])
plt.show()

• 각 인덱스 요소 간 차이 계산

print(eustockmarkets['SMI'])
print('--' * 20)

diff = eustockmarkets['SMI'].diff()
print(diff)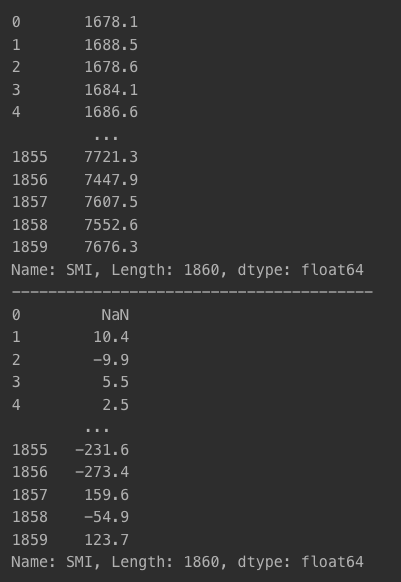

• 차분 적용한 DAX 히스토그램

plt.hist(diff)
plt.show()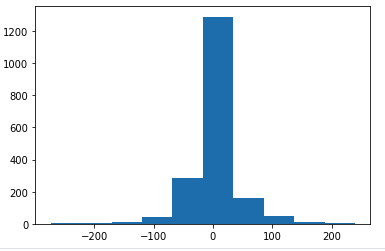

• SMI, DAX 비교

plt.scatter(eustockmarkets['SMI'], eustockmarkets['DAX'])
plt.show()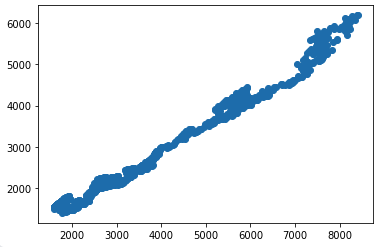

• 차분 적용된 SMI, DAX 비교

plt.scatter(eustockmarkets['SMI'].diff(), eustockmarkets['DAX'].diff())
plt.show()

3-3. 시계열에 특화된 EDA 방법

---

용어 정리

• 사인함수(Sine function)
  • 직각삼각형 두 변의 길이 중 빗변, 높이 길이 비
• 변수(Variable)
  • 데이터를 저장할 수 있는 메모리 공간
  • 변경 가능
• 허위 상관(Spurious correlation)
  • 통계적 상관은 있으나 인과관계가 없는 관계
• 자기 상관 함수(AutoCorrelation Function)
  • x축 : 시차(lag)
  • y축 : 자기상관(autocorrelation)
  • 시차가 0이라면 -> 자기 상관은 항상 1
  • 파란색 점선 : 임계값(95% 신뢰구간으로 추정되는 표준 편차)
  • 임계값 안에 들어가는 선은 통계적으로 중요하지 않음
• 부분(편)자기 상관 함수(Partial AutoCorrelation Function)
  • x축 : 시차(lag)
  • y축 : 부분 자기상관(Partial autocorrelation)

ACF(AutoCorrelation Function) Plot

• 자기 상관
  • 시계열 데이터에서 일정 간격 있는 값 사이의 상관관계
  • 시간에 따른 상관 정도 나타내기 위해 사용하는 통계량
  • 사인 함수, 사인함수의 ACF Plot
  • 임계값 파란색
    

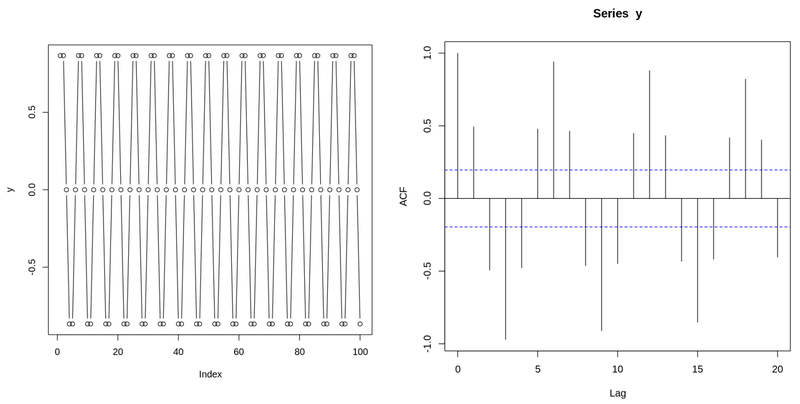
PACF(Partial AutoCorrelation Function) Plot

• 편자기 상관 함수
  • 자신에 대한 시차 편상관 의미
  • 두 시점 사이 전체 상관관계(시점 영향 요소들을 제외하고)에서 사이 다른 시점의 조건부 상관관계를 뺀 것
  • 사인 함수, 사인 함수의 PACF Plot
    

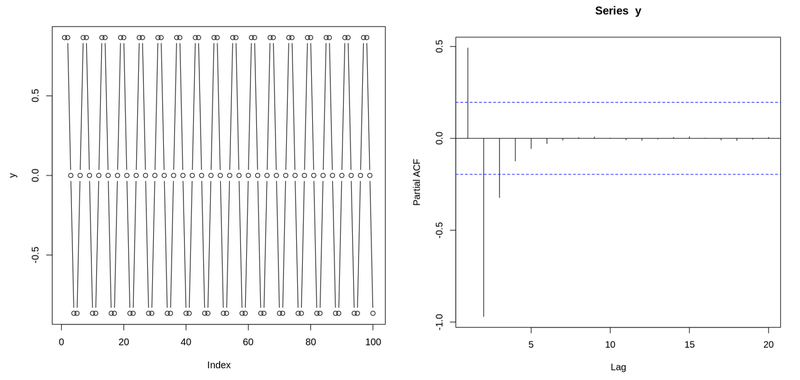
ACF와 PACF의 의미적 차이

• ACF : 두 시점 간 상관관계 계산 시 두 시점 사이 모든 lag 정보가 들어감
• PACF : 두 시점만의 상관관계만 계산(다른 lag -> 조건부 상관관계를 통해 제거하고 진행)

시계열 데이터 EDA

• 사용 라이브러리

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

• 사인 함수 생성
  • 0 ~ 99

x = np.array(range(100))
y = np.sin(x + np.pi/3)

plt.plot(y)
plt.show()

• acf

plot_acf(y)
plt.show()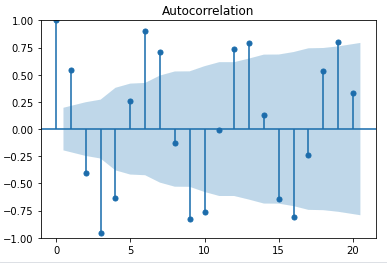

• pacf

plot_pacf(y)
plt.show()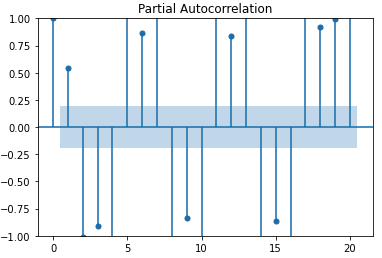

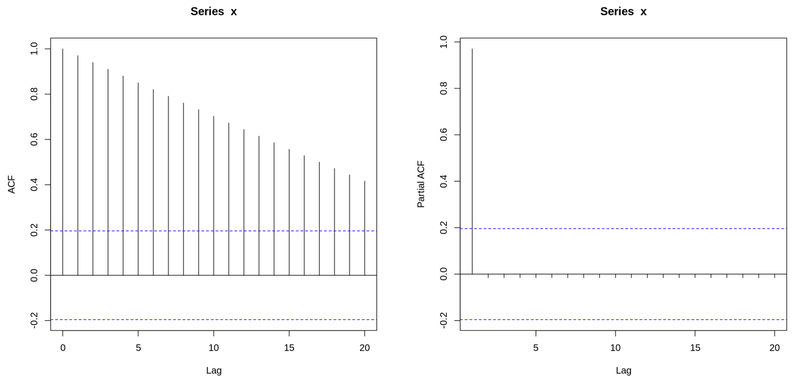
Non-stationary 데이터의 ACF 및 PACF

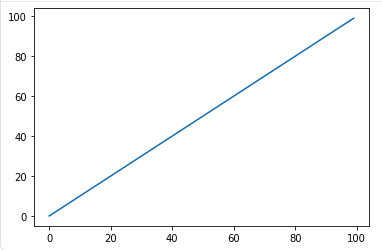
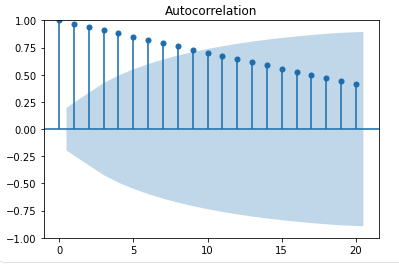
• 1 ~ 100까지 선형적 증가 데이터의 ACF 및 PACF plot

  • 크게 유의미하지 않음
  • 단순 균등 증가 -> PACF, ACF도 그닥 유용하지 않음
    

• 그래프
  

• acf
  

• pacf
  

시계열 EDA에서의 가장 중요한 위험

• 허위 상관(spurious correlation)
  • 두 개 이상 변수가 통계적 상관은 있으나, 인과관계가 없는 관계