Node 02. 시계열 데이터의 성질

2-1. 들어가며

---

학습 목표

• 시계열 기본 성질에서 시계열 요소 알아보기
• 정상성, 정상과정 알아보기

AirPassengers 데이터셋

• 1949년 ~ 1960년까지 월간 항공기 이용 승객수 기록 데이터셋
• 시계열 데이터
• 주요 특성 및 분석 시 특징이 뚜렷하여 교육용으로 많이 사용

시계열 요소

• 추세(Trend), 계절성(Seasonality), 주기성(Cycle)

핵심 키워드

• 정상성(Stationarity)
• 비정상성(Non-Stationarity)
• 정상과정(Stationary Process)
• KPSS(Kwiatkowski-Phillips-Schmidt-Shin) 검정
• ADF(Augmented Dickey-Fuller test) 검정

2-2. 시계열의 기본 성질

---

용어 정리

• 원시 데이터(Raw Data)

  • 가공되지 않은 측정 자료
  • 데이터 가공 과정을 거쳐 활용

• 잔차(residual)

  • $e = y - \hat{y}$
  • e : 에러, y : 실제 값, y hat : 예측 값
  • 잔차를 이용해 검증 가능한 지표 생성 가능

• 확률과정(stochastic process)

  • 시간의 흐름에 따라 관찰되는 확률 변수
  • 확률적 변화가 생기는 구조

• 표본(sample)

  • 많은 통계 자료 포함 집단에서 일부 추출

• 강한 가정(strong assumption)

  • 추정을 더 강하게 하는 것
  • 가정이 무너지면 -> 추정 의미 없어짐
  • 핵심적인 가정으로 추정을 하는 것

• 탐색적 데이터 분석(Exploratory Data Analysis)

  • 데이터 분석 시작 단계
  • 데이터 해체, 각 feature들이 어떤 것을 의미하는지 탐색 및 분석하는 것

• 평균(mean)

  • 주로 산술평균 사용
  • 데이터 모든 값에 대한 총합 -> 개수로 나눈 것
  • $\bar{x}$ = $x_1 + x_2 + x_n \over n$

• 편차(deviation)

  • 관측값 - 평균(or 중앙값)
  • $x - \bar{x}$

• 분산(variance)

  • 편차제곱의 평균
  • 데이터의 퍼짐 정도를 보는 것
  • $\frac{\sum (x_i - \bar{x})^2}{n}$

• 표준편차(Standard deviation)

  • 분산의 루트 값
  • 표준편차는 평균으로부터 원래 데이터에 대한 오차범위 근사값
  • $\sqrt{\frac{\sum (x_i - \bar{x})^2}{n}}$

시계열 요소

AirPassengers 데이터

• 1949년 1월 ~ 1960년 12월 승객 수 데이터

• 추세(trend)

  • 장기적 증가 or 감소 경향성이 존재하는 것을 의미
  • 시계열에서는 기울기 증가 or 감소 시 관찰됨
  • 일정 기간 동안 지속되는 변화(반복적 패턴은 아니어도 장기적 방향성 볼 수 있음)

• 계절성(seasonal)

  • 계절적 요인 영향으로 1년(일정 기간) 안에 반복적으로 나타나는 패턴
  • 빈도
  • 일정한 경우가 많음

• 주기성(Cycle)

  • 정해지지 않은 빈도, 기간에서의 상승 or 하락

요소별로 시계열 분해하기

• 시계열 기본 성질
  
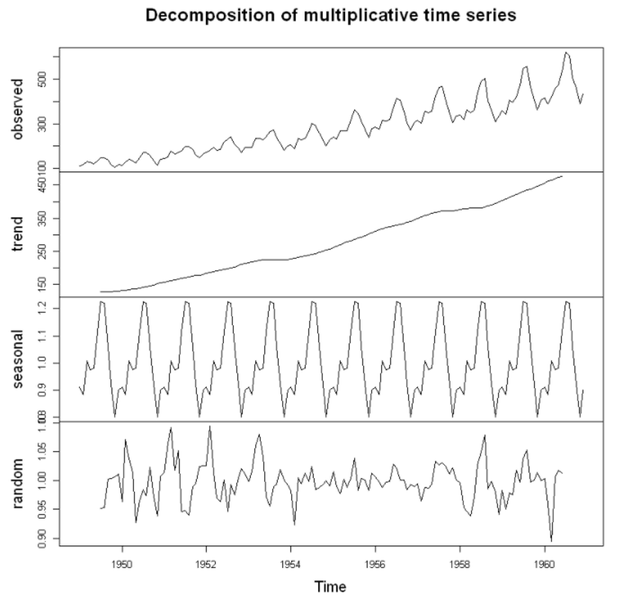
  • 이미지 출처 : 아이펠
  • observed : raw data(원본 값)
  • trend : 확정적 추세만 뽑아 시각화
  • seasonal : 비슷한 모양이 -> 구간별 12번 반복(1년마다 반복)
  • random : == 잔차, trend와 seasonal을 뺀 나머지, 더이상 뽑을 수 있는 시계열 기본 성질이 없어야 함!

시계열 정상성

• 정상성의 필요 이유 : 과거 시점 통계적 특징으로 미래에 적용
  • 정상성? : 안정된 수준

예측할 수 있는 것과 예측할 수 없는 것

• 현재 시간이 t일 경우
  • t-10 ~ t-1까지의 관측 시계열 특징 ≠ t ~ t+10
  • 이 경우, 앞의 시점으로 관측한 모델을 -> 후 시점에 적용할 수 있을까?
  • 이렇기 때문에 정상성이 필요한 것!

정상성

• 통계적 시계열 분석
  • 어떤 확률 과정을 따라는 시계열이 있다고 가정
  • 통계적 과정을 정확히 알아내는 것은 어려움
  • 그래서 강한 가정을 사용!
• 정상성이 강한 가정 중 하나임

정상 과정 (Stationary Process)

• 통계적 특성(평균, 분산 등)이 시간에 종속되지 않는 특징을 가짐
• 정상성을 띄는 확률 과정

2-3. 정상성이란?

---

정상성 (Stationarity)

• 시간 관계없이 시계열이 일정한 성질을 띠는 시계열
• 강정상성
  • 모든 적률(moments)이 시간과 무관하게 일정한 시계열
• 약정상성
  • 시간에 따른 일정한 평균, 분산, 공분산을 갖는 확률 과정
  • 어느 시점(t)에 관측하더라도 -> 확률 과정 성질이 변하지 않는 것!
  • 약정상시계열(weak stationary time series)
    • 임의의 t에 대해 $E(X_t) = \mu$
    • 임의의 t에 대해 $Var(X_t) < \infty$
    • 임의의 t, h에 대하여 $\text{Cov}(X_{t+h}, X_t) = \gamma(h)$(즉, 공분산이 h에만 의존)

정상성을 확인하는 방법

• KPSS(Kwiatkowski-Phillips-Schmidt-Shin Test) 검정
• ADF (Augmented Dickey-Fuller) 검정

KPSS 검정

• 귀무가설 : 시계열 과정이 정상적이다
• 대립가설 : 시계열 과정이 비정상적이다
• statsmodels 라이브러리 kpss 사용
  • 반환값 종류 : kpss_stat, p_value, lags, crit
  • p_value가 가장 직관적

from statsmodels.tsa.stattools import kpss

time_series_data_test = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

# KPSS 검정
kpss_outputs = kpss(time_series_data_test)

print('KPSS test 결과 : ')
print('--'*15)
print('KPSS Statistic:', kpss_outputs[0])
print('p-value:', kpss_outputs[1])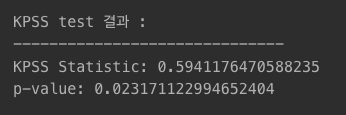

ADF 검정

• 귀무가설 : 시계열에 단위근이 존재한다
• 대립가설 : 시계열이 정상성을 만족한다
• statsmodels 라이브러리 adfuller 사용
  • 반환값 종류 : adf, pvalue, usedlag, nobs , critical values
  • 이 역시, p_value가 가장 직관적

from statsmodels.tsa.stattools import adfuller

time_series_data_test = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

# ADF 검정
adf_outputs = adfuller(time_series_data_test)

print('ADF Test 결과 : ')
print('--'*15)
print('ADF Statistic:', adf_outputs[0])
print('p-value:', adf_outputs[1])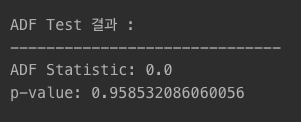

KPSS 검정 vs ADF 검정

• Deterministic Trend(확정적 추세)가 존재하면 -> 검정 결과에 차이 존재!
• KPSS 검정 -> 디폴트 옵션이 'around the mean' 검정이기 때문에 확정적 추세가 존재한다면 ADF와 달라질 수 있음

  시각적으로도 stationary한지 파악해야함

정상성 부여 방법

• 분산을 일정하게
• 평균을 일정하게

1️⃣ 분산을 일정하게 하는 방법

• 로그 변환(log transformation)

1. 단순 선형 -> 로그 변환 -> 비선형 특징을 가짐

time_series_data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

# 시계열 데이터 로그변환
time_series_data_log = np.log(time_series_data)

• time_series_data
  

• time_series_data_log
  

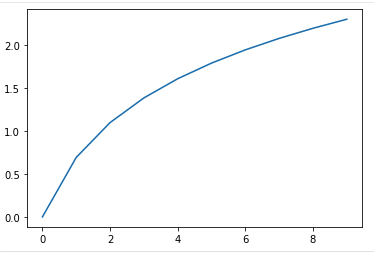
2. 로그 변환 시 일부 구간 선 끝의 완만, y축 값이 큰 값으로 줄어듦

time_series_data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

time_series_data = [random.randint(1, 100) for _ in range(50)]

time_series_data_log = np.log(time_series_data)

• time_series_data
  

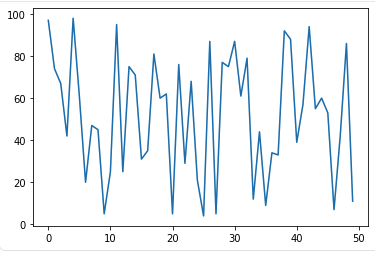
• time_series_data_log
  

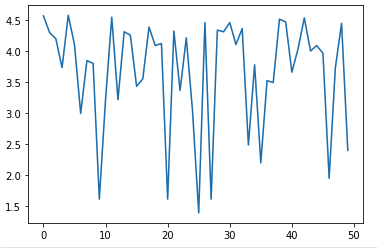
2️⃣ 평균을 일정하게 하는 방법

• 회귀, 평활, 차분

회귀(regression approach)

• 시계열 데이터를 선형 회귀 모델을 이용해 예측값과 실제값 차이를 내어 평균을 일정하게 조정
  • predictions : 예측값 $\hat{y}$

평활(smoothing)

• 시계열 데이터 잡음 제거를 위해 사용
• smoothed_value로 평활 확인

df0 = pd.DataFrame({'orig_value': [random.uniform(0, 100) for _ in range(100)]})
df1 = pd.DataFrame({'orig_value': [random.uniform(0, 100) for _ in range(100)]})

df0['smoothed_value'] = df0['orig_value'].rolling(5).mean()

# 잡음 포함 시계열 데이터
df0.plot(legend=True, title='original')

# 잡음 제거 시계열 데이터
df0.plot(legend=True, subplots=True, title='smoothed')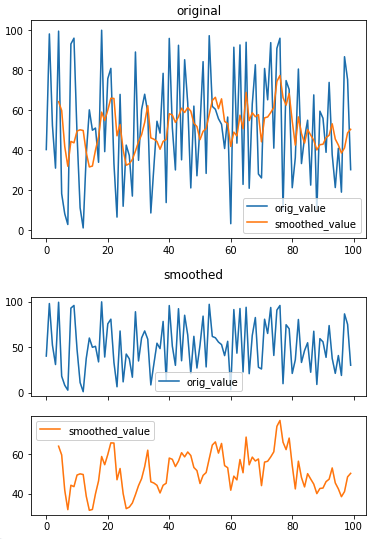

차분(differencing)

• 시계열 데이터간 시간 차이
• $y^*_t = y_t - y_{t-k}$
  • 1차 차분 : 1번의 차이를 구하는 것
  • 2차 차분 : 1차 차분값을 다시 차분하는 것
• 데이터 길이에 따라 더 수행될 수 있음

df1.plot(title='original')

# 차분 적용
df1['diff_value'] = df1['orig_value'].diff()
df1.plot(legend=True, subplots=True, title='diff')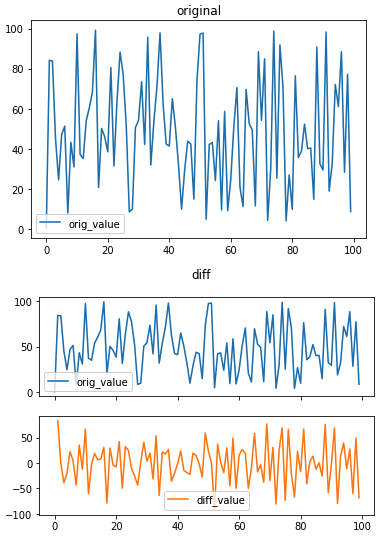

정리

• 비정상적 시계열 -> 누적 과정(Integrated Process)
• 정상적 시계열의 누적으로 비정상적 시계열이 이루어짐
• 즉, 그 누적을 차분해주면 -> 정상적 과정을 볼 수 있는 원리!