문제 정의

동일 등급의 와인 맛에 대한 변화로 인해 고객 클레임이 발생하여 해결하려 한다.
와인은 1-9등급까지의 등급이 있고 7등급부터 프리미엄 와인으로 고가에 판매가 되는데, 공정에서 최대한 많은 프리미엄 와인의 생산을 증대시키려고 한다.
품질 등급에 영향을 끼치는 공졍을 확인하여 일정한 맛의 와인을 프리미엄 등급으로 생산을 증대하고자 한다.

데이터 확인

소스코드 : GitHub

데이터 컬럼 상세

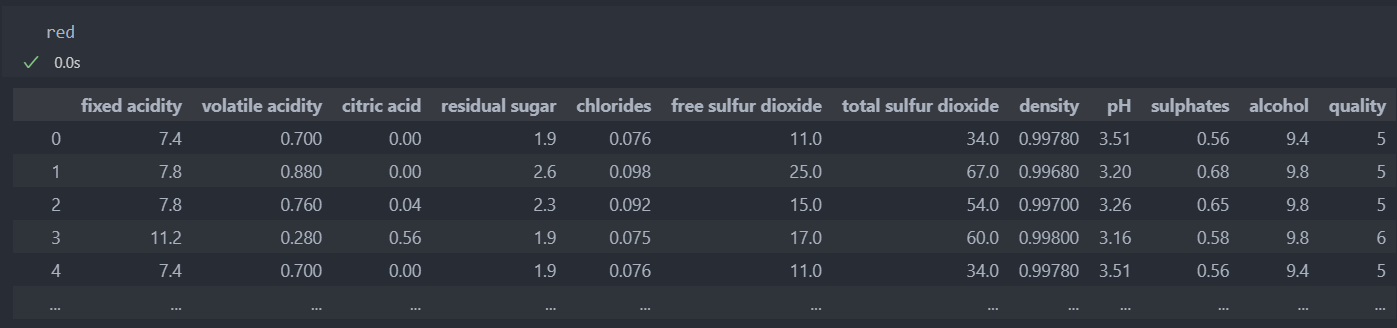
레드와인

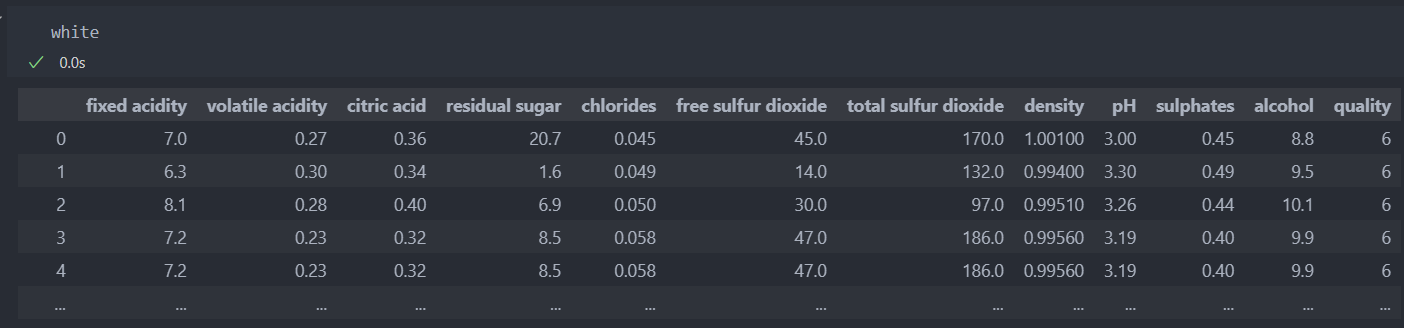
화이트 와인

EDA & 전처리

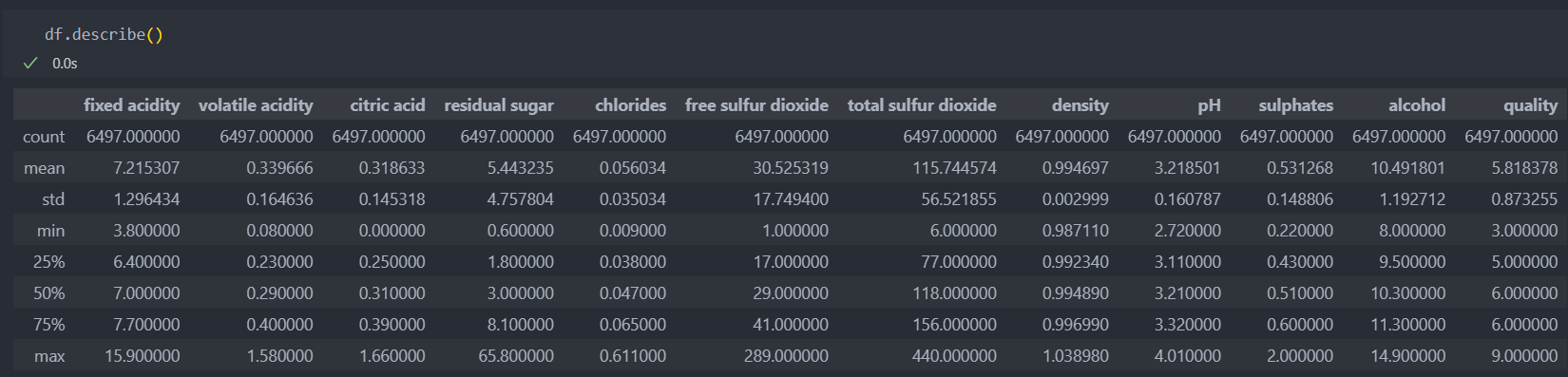
기본 정보

데이터의 가장 낮은 등급은 3이고 높은 등급은 9인데, 최소값과 최대값을 살펴보면 낮은 등급은 수치들이 대부분 낮은 분포를 가지고 있고 높은 등급은 높은 수치들의 분포를 가지고 있다.
평균값과 최대값의 차이는 눈에 띄게 차이가 나는 것은 아니지만,
좋은 등급은 첨가물 수치의 차이가 나는 것으로 예상된다.

모두 수치형 데이터들이다.

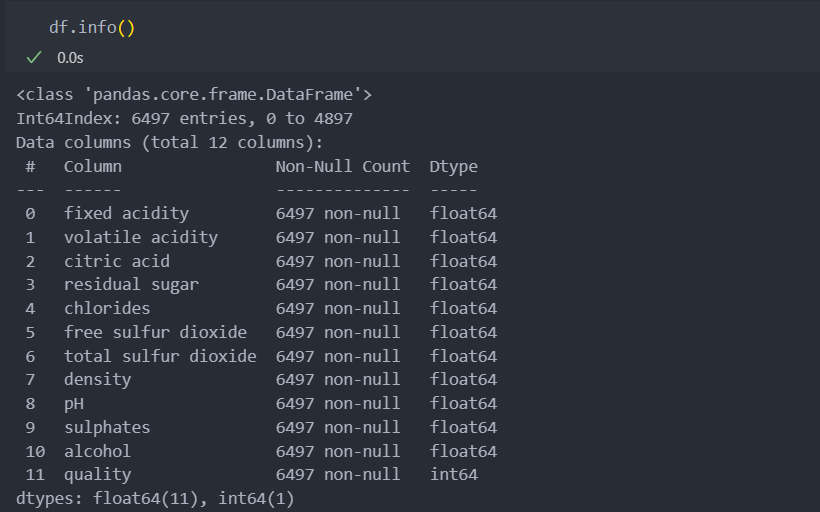
결측치는 없다.

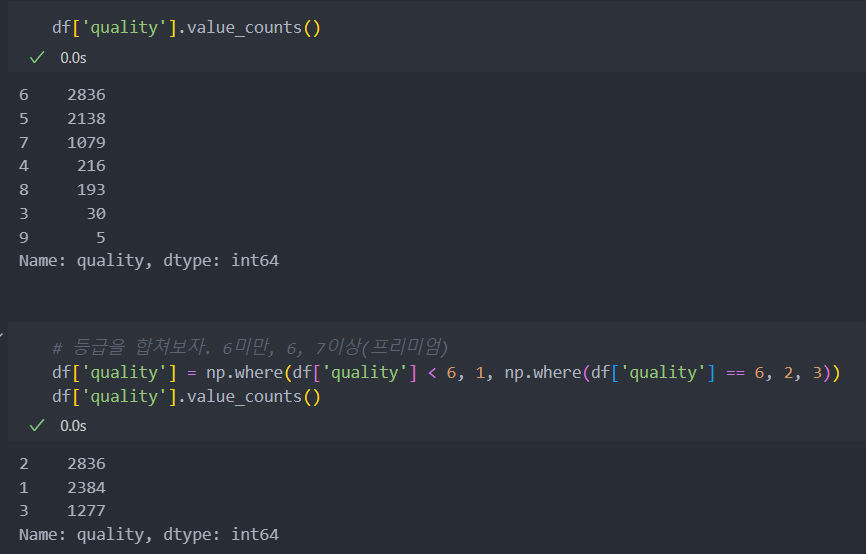
품질 정보 확인

품질의 정보가 세분화되어 있으나, 데이터가 세분화되어 있는 것에 비해서 데이터의 샘플이 적다.
그래서 가장 많은 품질 등급인 6을 중심으로 6보다 낮으면 1, 6이면 2, 6보다 높으면 3으로 등급을 분류한다.

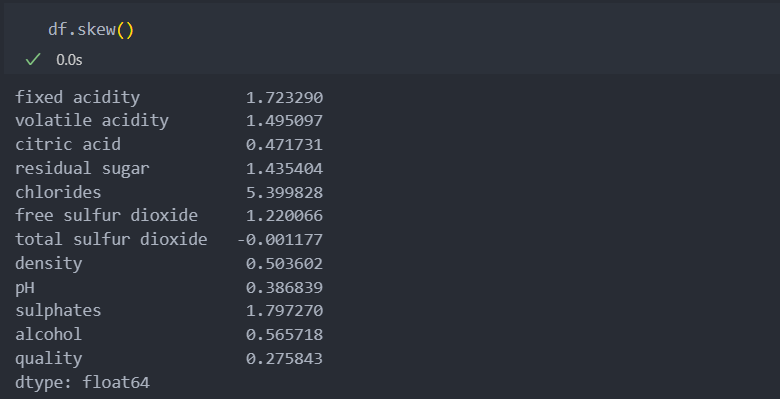
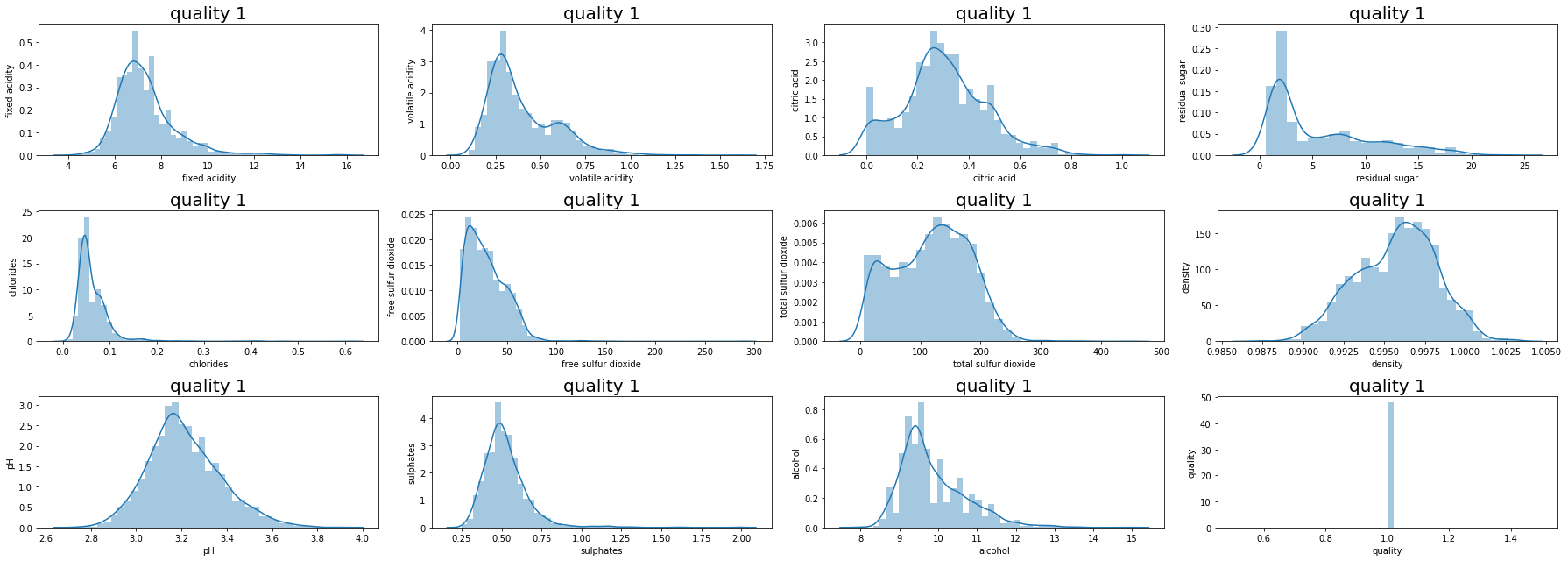
데이터들의 컬럼들의 데이터 분포도를 살펴보자.
3개의 컬럼이 1.5 수치를 넘는 것으로 비대칭성을 지니고 있다고 보인다.

대부분의 수치들이 왼쪽으로 치우쳐있는 것을 볼 수 있다.
여기에서 치우침을 완화할 것인지 고민을 해봐야 한다.
하지만 높은 등급을 가려내기 위해서 치우침 자체가 그 등급을 정한다면 치우침은 일단 그냥 두기로 한다.

for i in range(12):
    plt.subplot(3, 4, 1+i)
    plt.grid(False)
    sns.distplot(df.iloc[:, i])
    plt.ylabel(df.columns[i])

plt.gcf().set_size_inches(25, 9)
plt.tight_layout()
plt.show()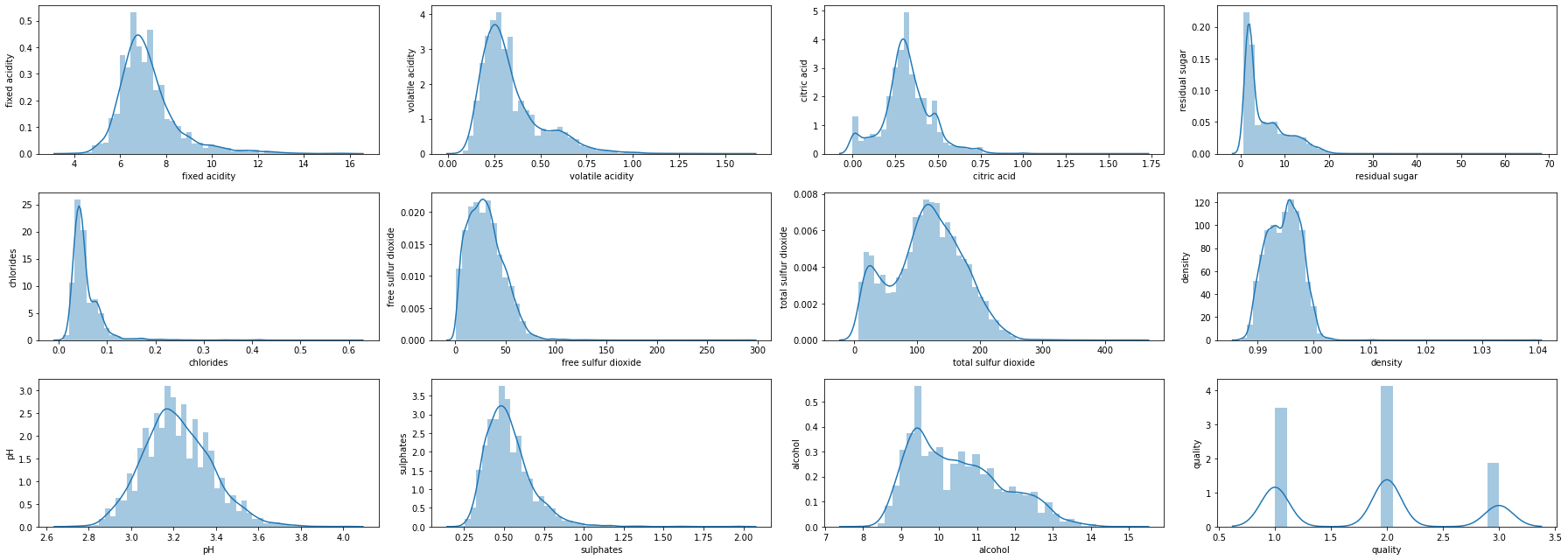

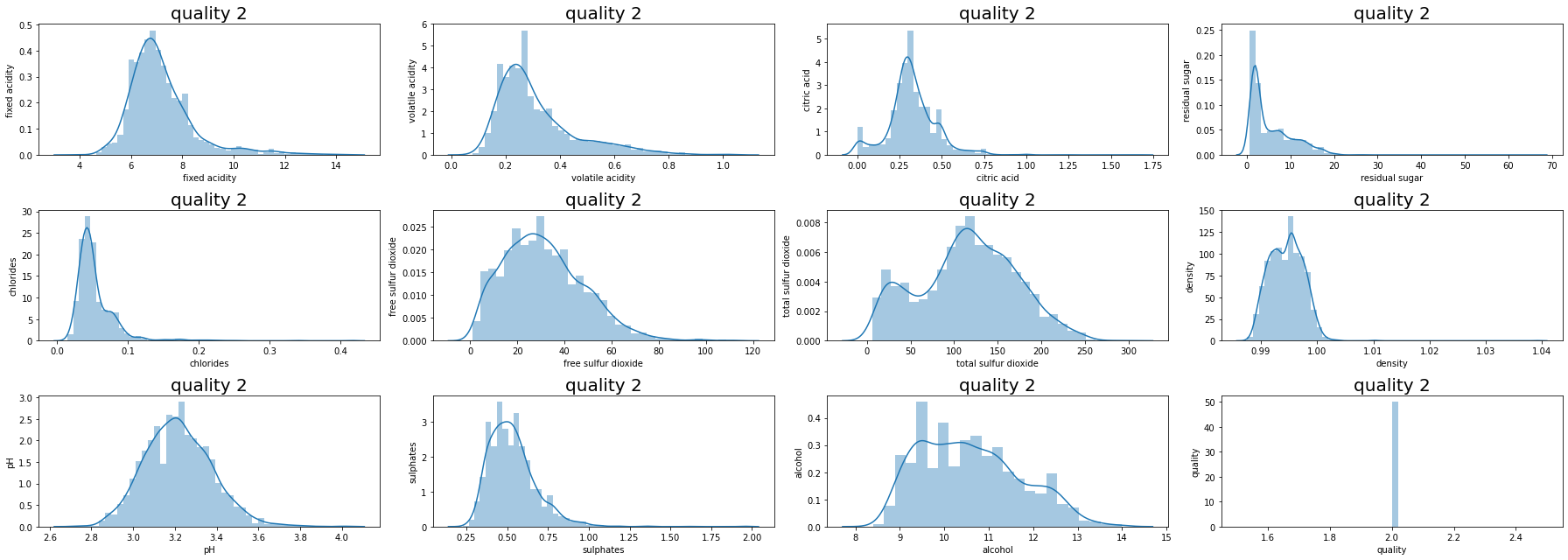
그럼 quality별로 그래프를 그려보자.
등급이 높아지면, 왼쪽으로 치우쳐있는 수치들이 오른쪽으로 수치들이 움직이는 것을 볼 수 있다.
수치 자체가 등급에 영향을 끼치는 것이 아닌지 다시 한 번 예측이 된다.
추가적으로 데이터의 샘플이 적어 레드 와인과 화이트 와인의 데이터를 섞었기 때문에 나타나는 데이터 수치일 수도 있다.

PCA & scaling

scaling

• 보통은 연속형 데이터들은 표준화나 정규화를 하게 되면 모델의 성능을 향상시킬 가능성이 있다.
• PCA를 진행하기 전에 scaling처리를 해야 성능이 보통 잘 나온다.

PCA

• 차원이 증가함에 따라 모델 학습 시간이 정비례하게 증가함(현재 데이터는 샘플이 적어서 학습 시간에 영향이 없어 보인다)
• 차원이 증가함에 따라서 각 결정 공간에 포함되는 샘플 수가 적어져, 과적합으로 인해 성능 저하 발생.

PCA를 2개를 적용시켜 그 값의 평균을 기준으로 다시 등급을 분리하여 진행하도록 한다.

이제 StandardScaler(표준화) scaling과 PCA(데이터 컬럼들의 차원 축소)를 적용해보자.
참조 : 변수 분포 문제

PCA를 적용하였을 때, 축소한 각 차원의 설명력(ratio)과 설정한 설명력 이상을 적용할 때 선택할 차원 수 반환 함수를 작성해보자.

# PCA 적용
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline

def pca_feature_var(data, ratio): # ratio : 축소한 각 차원의 설명력(모든 차원의 설명력 합 = 1), 보통 0.9 이상의 높은 설명력을 가지는 차원들 선택
    roop_idx = data['quality'].unique() # 품질 등급

    fig, ax = plt.subplots(len(roop_idx), 1, figsize=(20, 12))

    for i, x in enumerate(roop_idx): # 품질 등급별 PCA 적용
        df1 = data[data['quality']==x]
        X = df1.drop('quality', axis=1)

        # scaling
        scaler = StandardScaler()

        # PCA 적용
        pca = PCA()

        # pipeline : scaler와 pca 적용을 묶어서 사용 가능하도록
        pipeline = make_pipeline(scaler, pca)

        # 학습
        pipeline.fit(X)
        features = range(pca.n_components_)

        feature_df = pd.DataFrame(data=features, columns=['pc_feature'])
        variance_df = pd.DataFrame(data=pca.explained_variance_ratio_, columns=['variance'])
        pc_feature_df = pd.concat([feature_df, variance_df], axis=1)

        cumsum = np.cumsum(pca.explained_variance_ratio_)
        d = np.argmax(cumsum >= ratio) + 1 # argmax 가장 높은 값을 가지는 값의 인덱스 반환, ratio(설명력)보다 큰 값을 가지는 차원 수 선택, +1(인덱스는 0부터 시작)
        singular_vector = pd.DataFrame(pca.components_.T, index=X.columns)

        print('quality :', x, '/ 선택할 차원 수 :', d, '변수 설명력 :', cumsum[d-1])
        print(singular_vector)
        print('-'*40)

        sns.barplot(ax=ax[i], x='pc_feature', y='variance', data=pc_feature_df)
        plt.xlabel('PCA feature')
        plt.ylabel('variance')
    plt.show()

x축은 차원을 축소시켰을 때의 차원, y축은 차원별 설명력.

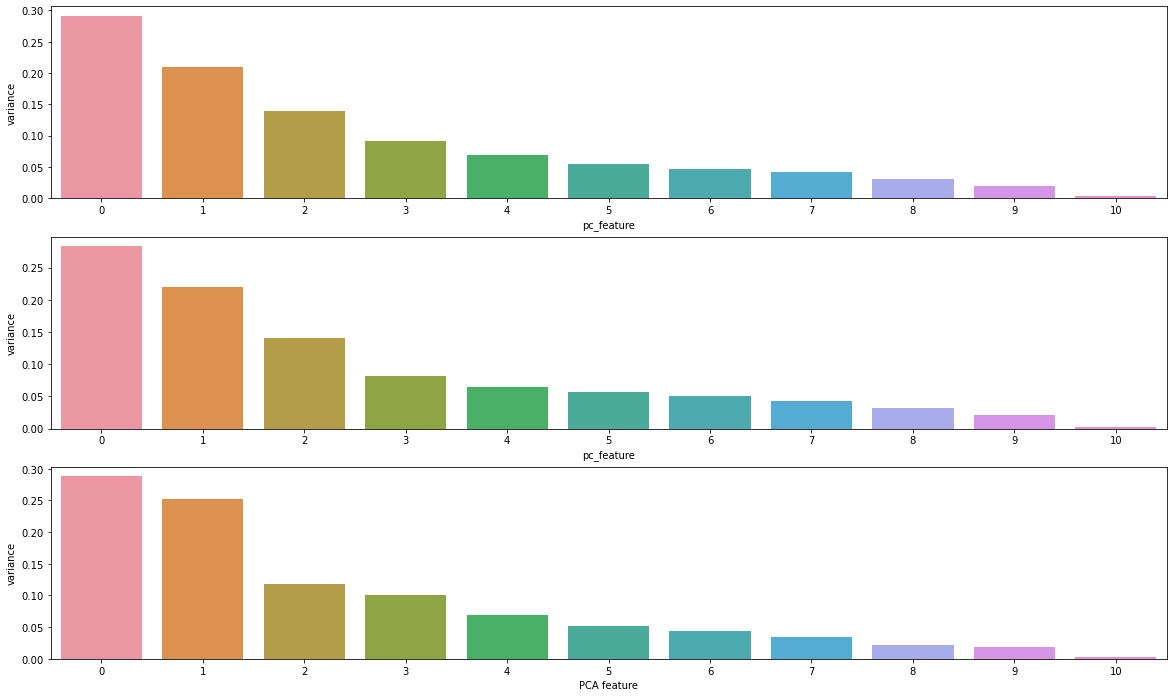
보통 특징(컬럼)들의 상관성이 높을 때, 그 상관성을 없애기 위해서 사용할 때 PCA의 설명력 0.9 이상의 차원들을 선택한다.
하지만 기존의 컬럼들을 사용하면서 PCA 차원을 기존의 데이터에 추가하기 위해 가장 높은 설명력을 갖는 2개의 차원만 선택하도록 한다.
PCA(n_components = 2) 적용

여기에서 고민해 봐야할 것은, 데이터 샘플에 비해서 특징(컬럼)이 많은 편에 속하기에 특징을 늘리는 형태가 되어 상태 공간의 크기가 커짐에 따라서 모델의 성능을 이끌어 낼 수 있을지를 생각해야 한다.
차원 축소를 진행했을 때 축소한 데이터만 사용한다면(ex. 설명력 0.9이상을 선택), 데이터를 설명할 수 있는 설명력이 기존보다 0.1부족한 데이터 설명력을 가지게 된다. 그래서 기존 데이터의 정보 손실과 특징(컬럼)이 너무 많아 상태 공간이 커짐으로 인해 모델의 성능을 이끌어낼 수 있는지 여부는 실제로 각각의 케이스를 모두 진행해 봐야 한다.(정보 손실 VS 상태 공간)

하지만 이번 진행은 데이터 중에서 어느 특징(컬럼)이 PCA를 진행한 2개의 차원 평균 값에 영향을 많이 미치는지 확인하기 위한 것이다.
즉, PCA의 분포를 기준으로 평균값에 가까운지 멀어지는지를 가지고 진행한다.

축소된 차원의 그래프를 등급별로 확인해보자.
중심에서 멀어질수록 공정 변수의 평균과 떨어진 데이터인데, 중심에서 멀어진 데이터들이 등급에 맞는 맛과 다른 품질을 가지는 데이터라는 것을 유추해볼 수 있다.

 def pca_plot(df,y) :

       x=df.drop(['quality'], axis=1).reset_index(drop=True)
       y=df[y].reset_index(drop=True)

       X_ = StandardScaler().fit_transform(x)

       pca = PCA(n_components=2)
       pc = pca.fit_transform(X_)

       pc_df=pd.DataFrame(pc,columns=['PC1','PC2']).reset_index(drop=True)
       pc_df=pd.concat([pc_df,y],axis=1)

       plt.rcParams['figure.figsize'] = [10, 10]
       sns.scatterplot(data=pc_df,x='PC1',y='PC2',hue=y, legend='brief', s=100, linewidth=0)
       
pca_plot(df,'quality')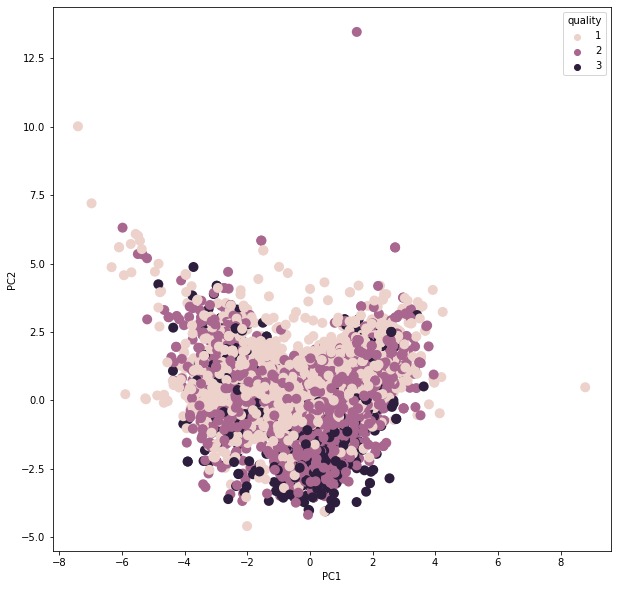

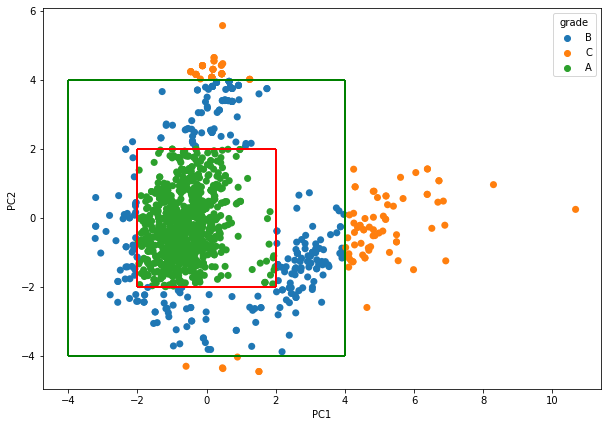
PCA 차원을 통한 등급화 및 시각화

이제 기존의 데이터에 PCA 데이터를 추가시킬 것인데, 품질 등급별로 진행을 할 것이다.
중심과의 거리를 통해 한번 더 등급을 부여할 것이다.
중심과 가까울수록 공정에 맞는 데이터로써 A, B, C로 나누는 작업을 각 등급 1, 2, 3등급별로 진행한다.
그 기준은 위의 PCA를 통한 차원 축소를 한 2가지 특징을 가지고 기준을 나눌 것이다.

품질 등급 : 1

품질 등급이 1에 해당하는 데이터만 불러와서 차원 축소한 값을 추가하여 진행한다.

# 품질(Quality) 등급을 부여하기 위해, PC1값과 PC2값을 기존 데이터에 concat

df1=df[(df['quality']==1)] # 품질 1
X=df1.drop(['quality'], axis=1)
X_ = StandardScaler().fit_transform(X)

pca = PCA(n_components=2)
pc = pca.fit_transform(X_)

pc_df=pd.DataFrame(pc,columns=['PC1','PC2'])

df1_concat = pd.concat([df1.reset_index(drop=True), pc_df], axis=1)

그리고 'grade' 컬럼을 추가하여 축소한 차원 2개를 가지고 등급을 부여한다.
'grade'를 부여할 때, 중심에서 2미만인 데이터는 A, 4미만은 B, 그 외에는 C로 분리를 하였다.
품질의 등급을 조금 더 좁게 잡아서 진행하려면 2가 아닌, 1.5나 그 이하의 수를 적용하면 되겠다.

#  np.where 활용하여 등급 나누기
df1_concat['grade'] = np.where( (df1_concat['PC1']>-2) & (df1_concat['PC1']<2) & (df1_concat['PC2']>-2) & (df1_concat['PC2']<2), 'A', 
                               np.where((df1_concat['PC1']>-4) & (df1_concat['PC1']<4) & (df1_concat['PC2']>-4) & (df1_concat['PC2']<4), 'B', 'C') )

이제 나눈 등급을 기준으로 산점도 그래프로 시각화를 해보면 아래와 같다.

sns.scatterplot(data=df1_concat,x='PC1',y='PC2', s=50, linewidth=0, hue='grade');

# ▶ A grade
plt.vlines(-2, ymin=-2, ymax=2, color='r', linewidth=2);
plt.vlines(2, ymin=-2, ymax=2, color='r', linewidth=2);

plt.hlines(-2, xmin=-2, xmax=2, color='r', linewidth=2);
plt.hlines(2, xmin=-2, xmax=2, color='r', linewidth=2);

# ▶ B grade
plt.vlines(-4, ymin=-4, ymax=4, color='g', linewidth=2);
plt.vlines(4, ymin=-4, ymax=4, color='g', linewidth=2);

plt.hlines(-4, xmin=-4, xmax=4, color='g', linewidth=2);
plt.hlines(4, xmin=-4, xmax=4, color='g', linewidth=2);

plt.gcf().set_size_inches(10, 10)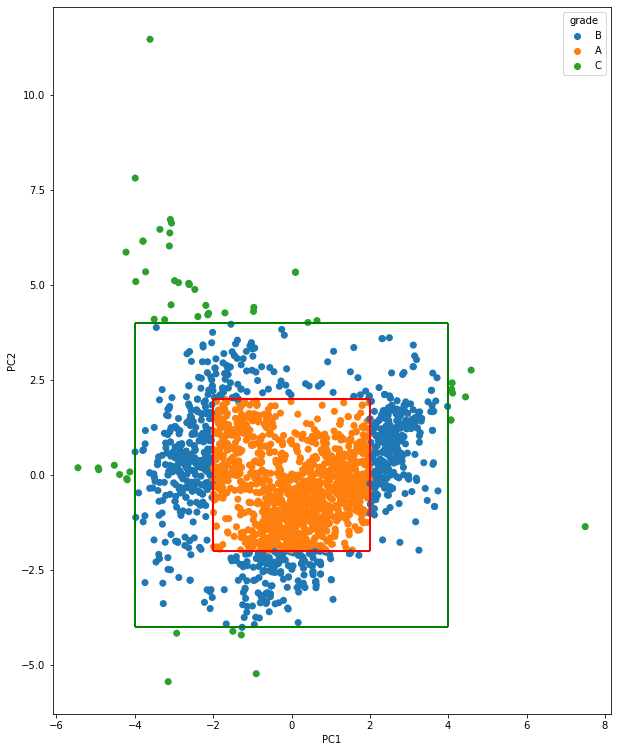

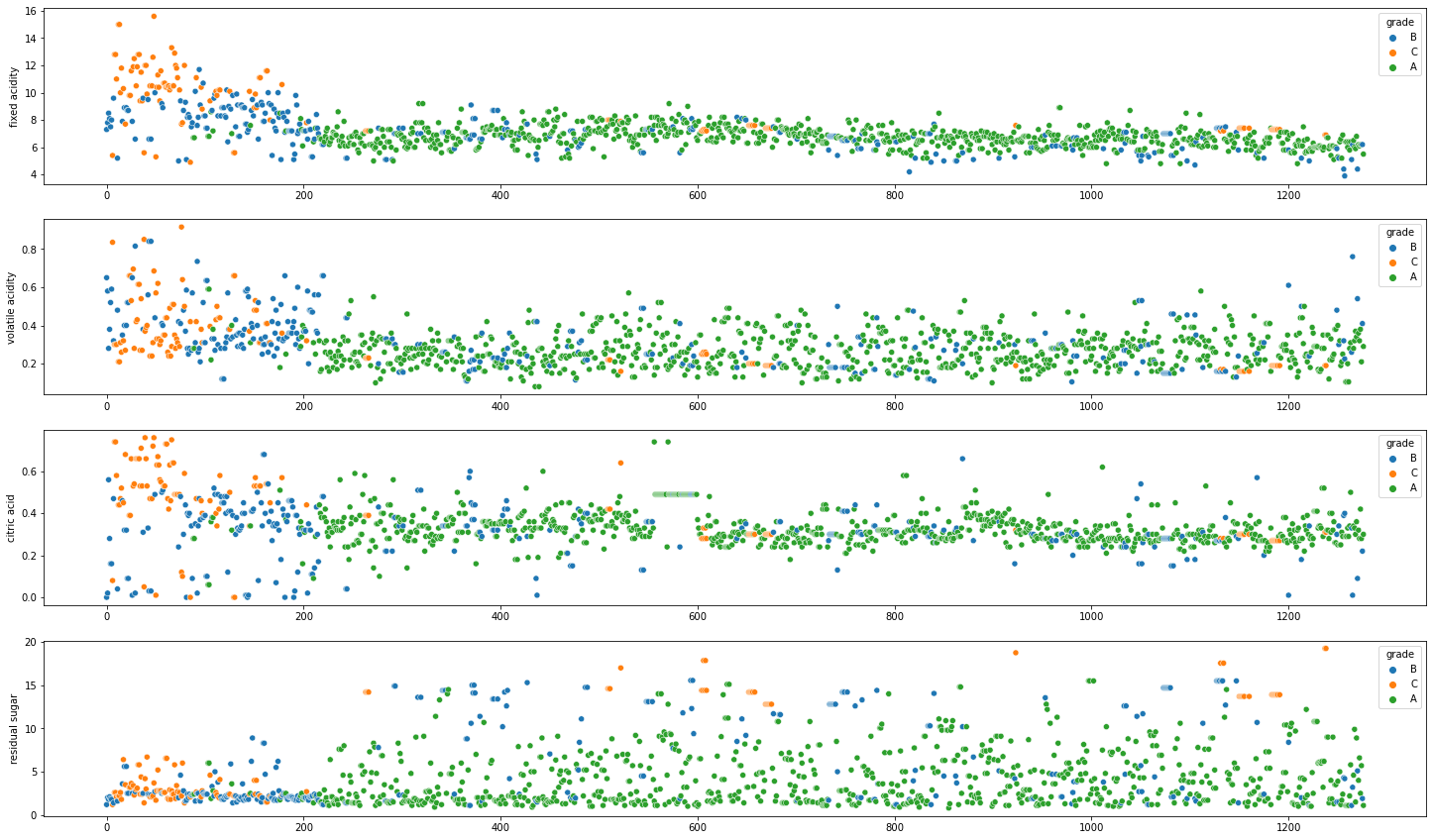
축소한 차원으로 등급을 나눈 것을 가지고 기존의 데이터의 컬럼과 비교하여 어떻게 차이가 나는지 확인해보자.
아래와 같이 1등급의 와인이라도, C등급은 모든 공정변수 기준으로 평균값(center) 값에서 멀어지는 경향이 있음을 알 수 있다.

fig, axes = plt.subplots(4, 1)
sns.scatterplot(x=df1_concat.index, y=df1_concat['fixed acidity'], hue = df1_concat['grade'], ax=axes[0]);
sns.scatterplot(x=df1_concat.index, y=df1_concat['volatile acidity'], hue = df1_concat['grade'], ax=axes[1]);
sns.scatterplot(x=df1_concat.index, y=df1_concat['citric acid'], hue = df1_concat['grade'], ax=axes[2]);
sns.scatterplot(x=df1_concat.index, y=df1_concat['residual sugar'], hue = df1_concat['grade'], ax=axes[3]);
plt.gcf().set_size_inches(25, 15)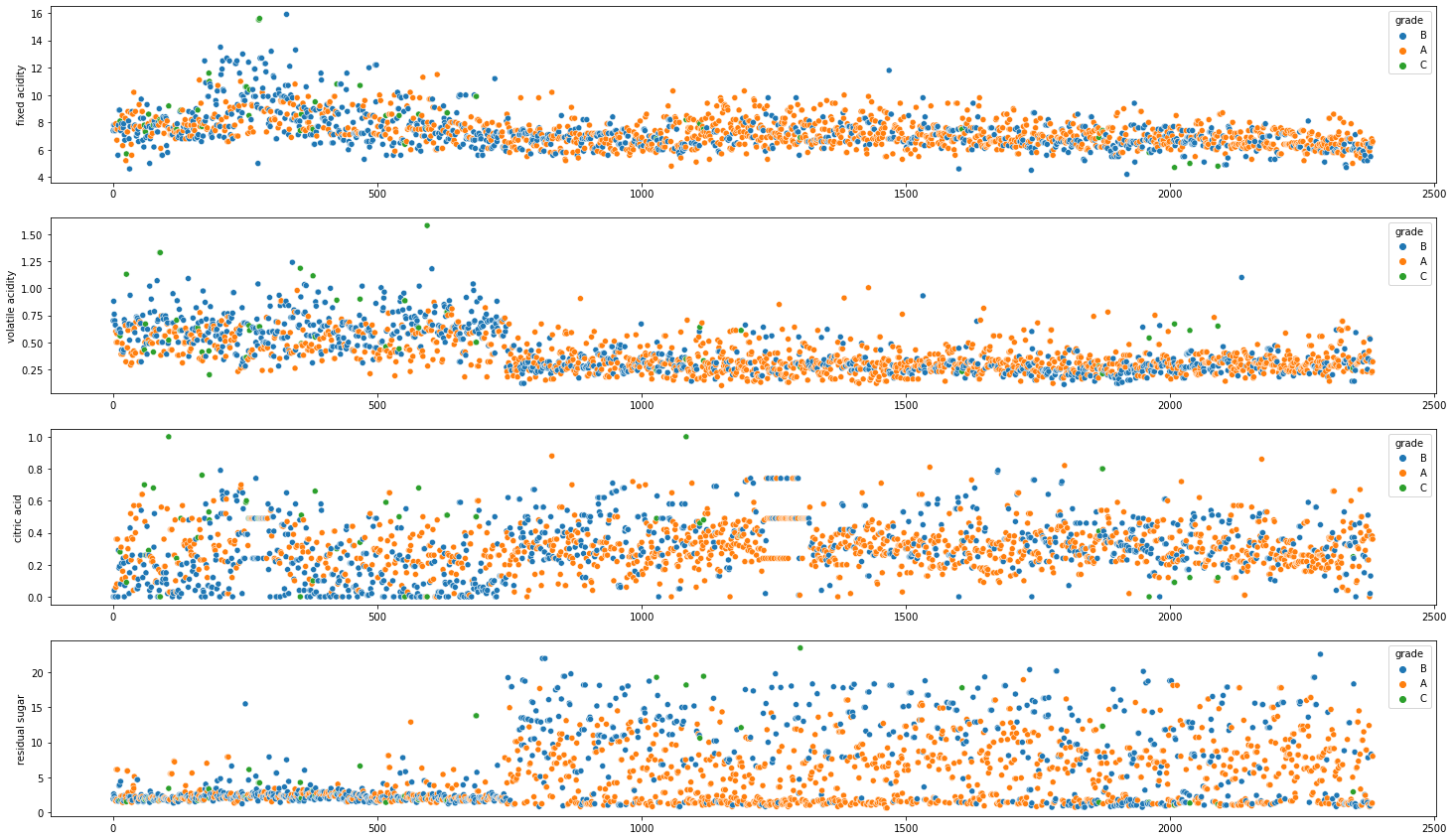

품질 등급 : 2

품질 등급이 2에 해당하는 데이터만 불러와서 차원 축소한 값을 추가하여 진행한다.
방법은 품질 등급 1과 똑같이 진행한다.

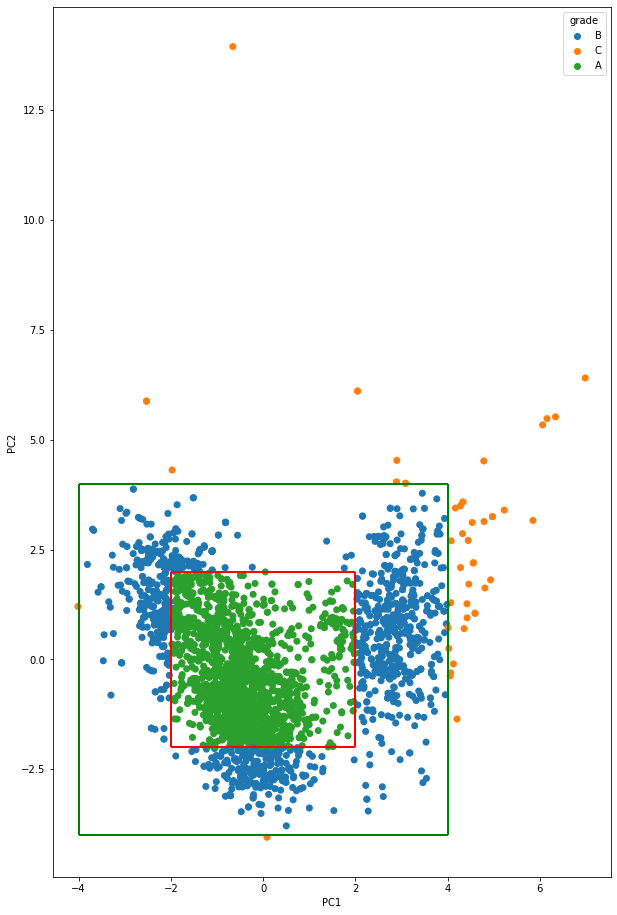
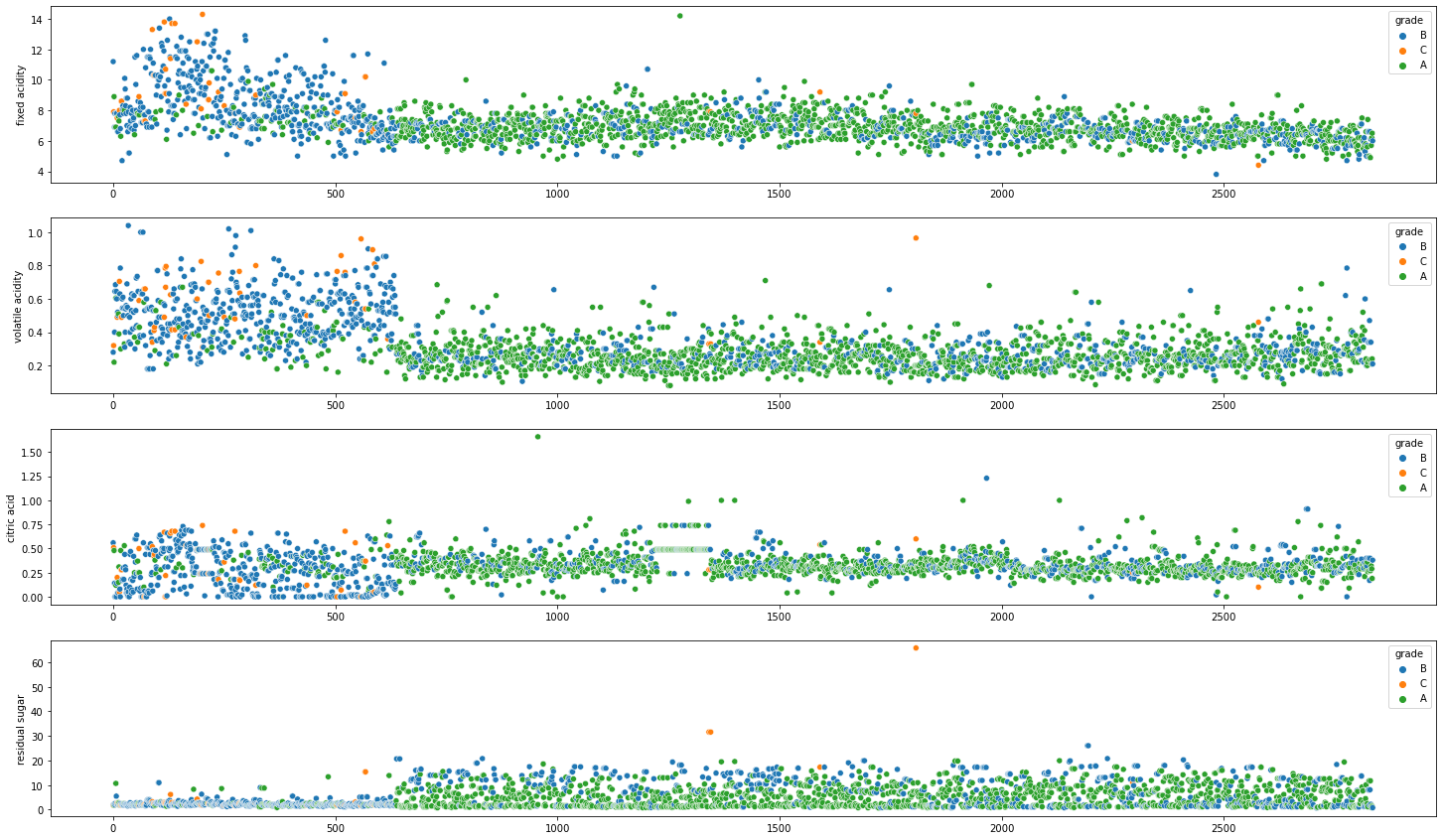
품질 등급 : 3

품질 등급이 3에 해당하는 데이터만 불러와서 차원 축소한 값을 추가하여 진행한다.

해당 데이터는 타겟 데이터의 기준치가 없기 때문에, 2차원으로 축소한 데이터의 평균값을 기준으로 다른 특징(컬럼)들의 분포를 타겟 데이터로 설정하였다.
등급별로 기존의 데이터의 컬럼과 비교하면 대체로 특징별로 A등급은 평균에 모여있고 B, C는 상대적으로 평균치에서 떨어져있는 데이터들이 조금 더 많다는 것을 확인할 수 있다.
앞쪽의 데이터들이 차이나는 이유는 레드 와인과 화이트 와인을 합쳤기에 차이가 나는 부분일 것이라 짐작이 된다.

그러면 어느 특징(컬럼)들이 와인의 품질에 영향을 많이 끼치는지 확인해보자.

모델링

어느 특징(컬럼)이 'grade'를 예측하는데 중요한 특징으로 작용하는지 확인하기 위해 학습 및 예측을 진행해보자.
모델은 트리 게열의 앙상블 모델인 RandomForestClassifier 사용할 것이다.
품질 등급별로 등급을 나누는데 있어 가장 크게 작용하는 특징이 있는지 살펴보자.

필요한 모듈들을 받는다.

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import mean_absolute_error as MAE
from sklearn.model_selection import ParameterGrid
from sklearn.feature_selection import *

그리고 MAE를 계산하기 위해서 라벨 데이터는 숫자형으로 바꿔주는 함수를 먼저 간단히 만든다.

def get_grade(x):
    if x == 'A':
        x = 1
    elif x == 'B':
        x = 2
    elif x == 'C':
        x = 3
    
    return x

품질 등급 : 1

먼저 데이터를 나눈다.

X=df1_concat.drop(['quality', 'PC1', 'PC2', 'grade', 'n_grade'], axis=1)
Y=df1_concat['n_grade']

train_x, test_x, train_y, test_y = train_test_split(X, Y, stratify=Y)

train_x.shape, train_y.shape, test_x.shape, test_y.shape

그리고 하이퍼 파라미터를 설정하고

param_grid = ParameterGrid({
                            'n_estimators':[200, 300, 400, 500, 600],
                            'max_depth':[2, 5, 10, 15, 20],
                            'random_state':[29, 1000]
})

학습을 진행한다.

best_score = 1e9

for i, p in enumerate(param_grid):
    model = RandomForestClassifier(**p).fit(train_x, train_y)
    pred = model.predict(test_x)
    score = MAE(test_y, pred)

    if score < best_score:
        best_score = score
        best_param = p

score 점수가 가장 낮은 best score 성능을 내는 하이퍼 파라미터를 확인한다.

print(f'best_param : {best_param}')

결과:
best_param : {'max_depth': 20, 'n_estimators': 200, 'random_state': 1000}

재학습을 진행한다.

model = RandomForestClassifier(**best_param).fit(train_x, train_y)

train_pred = model.predict(train_x)
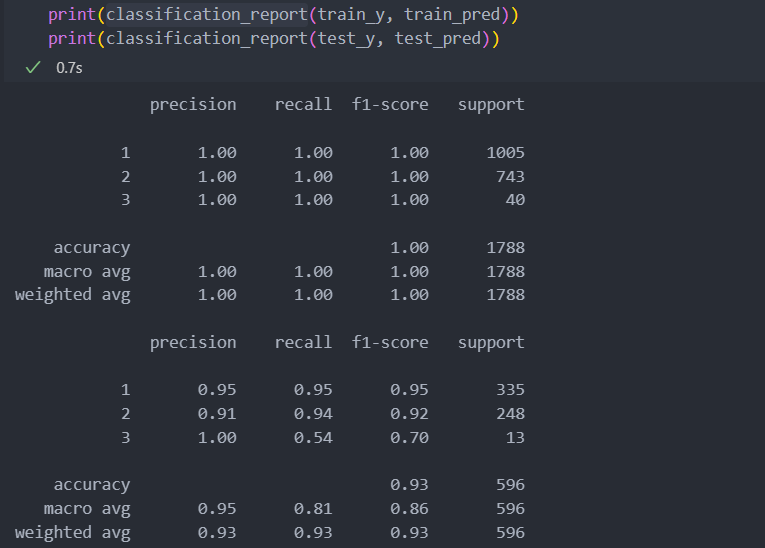
test_pred = model.predict(test_x)

학습을 진행한 classification report를 확인해보자.
3등급의 재현율이 다른 평가 지표들보다 낮은 것을 볼 때, C등급(3)으로 매긴 수치들에서 생산된 와인의 맛이 일정하지 않을 것이라고 예측이 된다.

마지막으로 등급을 나누는데 있어 가장 크게 작용하는 특징(컬럼)을 확인해보자.

ftr_importances_values = model.feature_importances_
ftr_importances = pd.Series(ftr_importances_values, index = train_x.columns)
ftr_top20 = ftr_importances.sort_values(ascending=False)[:20]

plt.figure(figsize=(8,6))
plt.title('Feature Importances')
sns.barplot(x=ftr_top20, y=ftr_top20.index)
plt.show()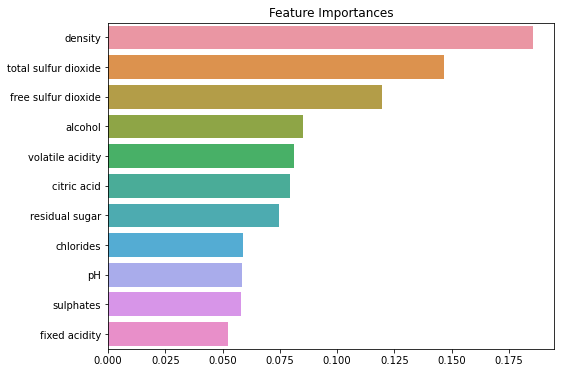

품질 등급 : 2

품질 등급 : 1을 확인할 때와 똑같이 진행하면 된다.

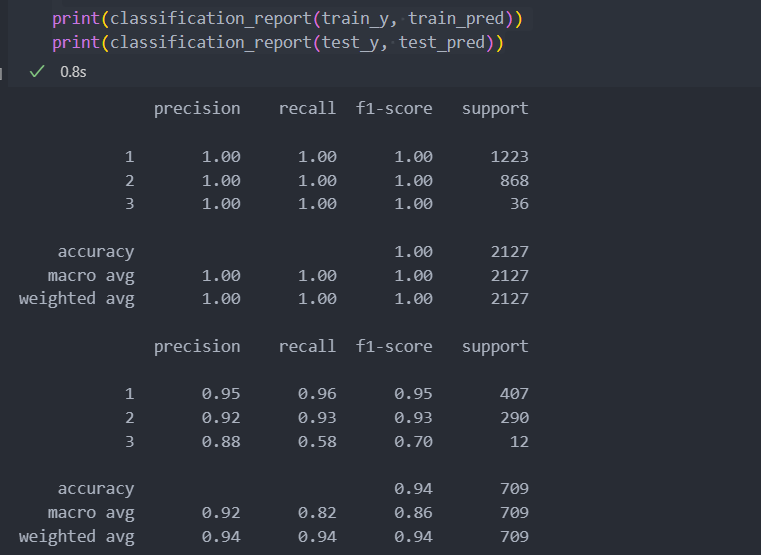
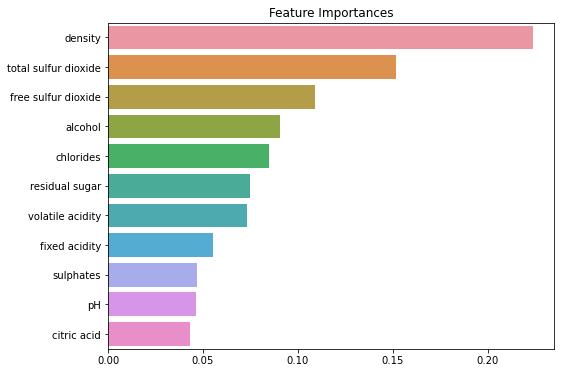
품질 등급 : 3

품질 등급 : 1을 확인할 때와 똑같이 진행하면 된다.

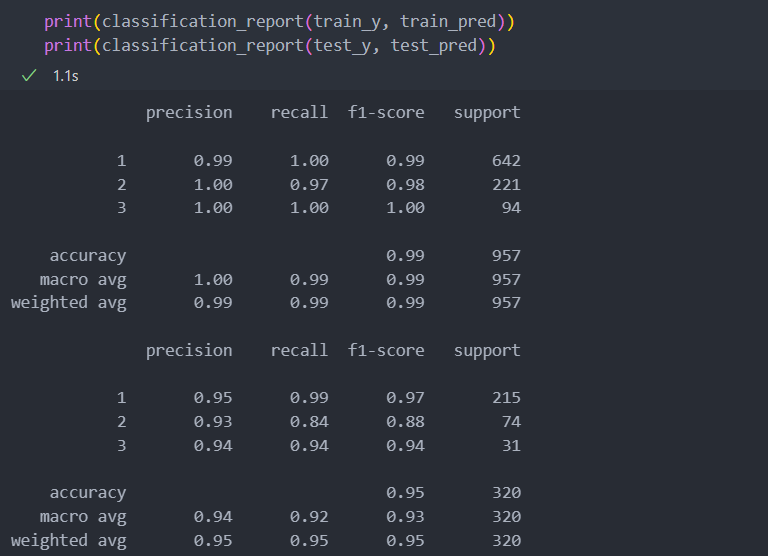
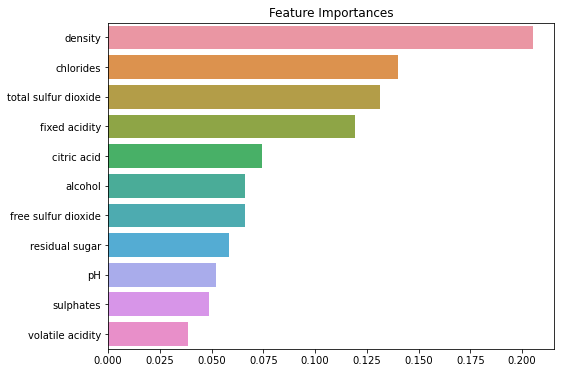
특징

품질 등급이 결정될 때, 공통적으로 가장 크게 영향을 미치는 특징은 아래와 같다.
맛의 일정함을 유지하기 위해서는 아래의 특징들을 공정 중에 특히 신경써야하는 부분이다.

• density : 밀도
• total sulfur dioxide : 총 이산화황
• chlorides : 염화물
• alcohol : 도수

기대효과

일정한 맛으로 인해 고객 클레임을 줄이고 회사 이미지를 긍정적으로 변화시킬 수 있다.

다음 챕터에서 고급(3등급 : 프리미엄 등급)의 생산 증대를 위한 분석을 이어서 진행하겠다.