문제 정의

(태양렬 발전)전력 발전량은 기상 날씨에 따라 변동이 심하기 때문에 전력 예산 수립에 어려움을 겪고 있다.
2017년 1년치에 대한 데이터를 활용하여 전력발전량 예측하는 모델을 만들고 일기예보에 데이터를 활용하여 전력발전량을 예측 및 전력사용계획을 세우고자 한다.
기상 데이터를 활용하여 전력발전량을 예측하는 문제이나,
실제 기상 데이터를 미리 예측하는 것이 어렵기 때문에 기상 데이터의 정확도가 높을 수록 전력발전량도 높은 확률로 예측이 가능할 것이라고 본다.

데이터 확인

소스코드 및 데이터 : GitHub

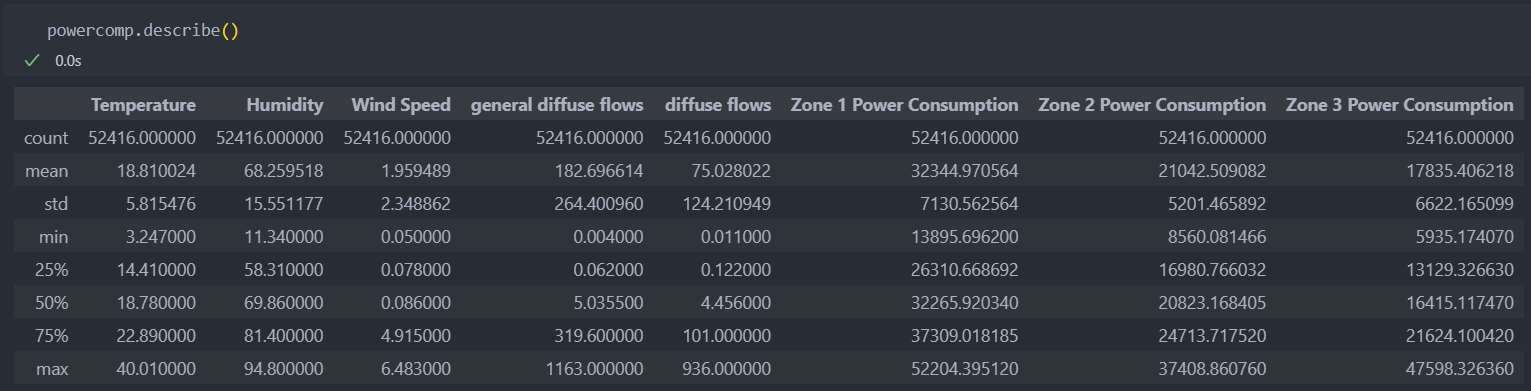
• powercomp.csv : 10분 단위로 기상 데이터 및 전력 발산량과 각 위치(Zone1~3)의 발전량이 기록
  
  -Temperature : 온도
  -Humidity : 습도
  -Wind Speed : 풍속
  -general diffuse flows : 전력 발산량(일반)
  -diffuse flows : 전력 발산량(실제)
  -Zone 1-3 Power Consumption : 1-3 Zone 발전량

EDA & 전처리

데이터 탐색

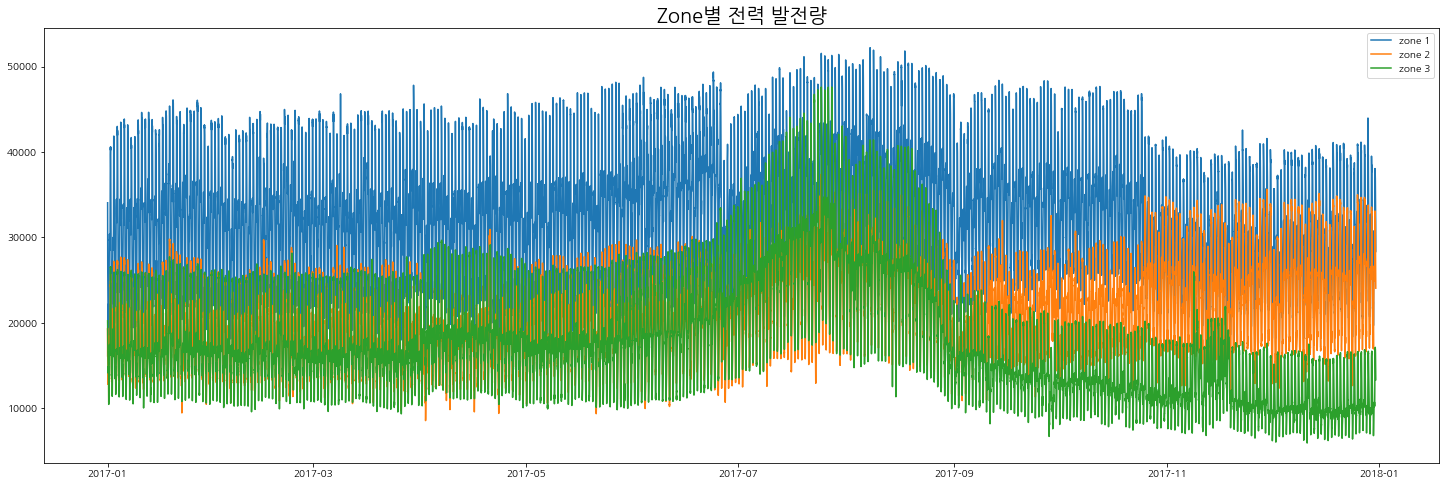
Zone별로 보았을 때 1 -> 2 -> 3 순으로 전력 발전량이 많은 것을 확인할 수 있다.

그리고 데이터의 결측치(결측치 없음)를 확인하고, 날짜의 타입을 datetime형식으로 바꿔서 시간별 측정을 할 수 있도록 한다.
datetime형식으로 타입을 바꾸려면 바꾸기 전 데이터의 타입은 문자형이어야 한다.

Zone별 전력량

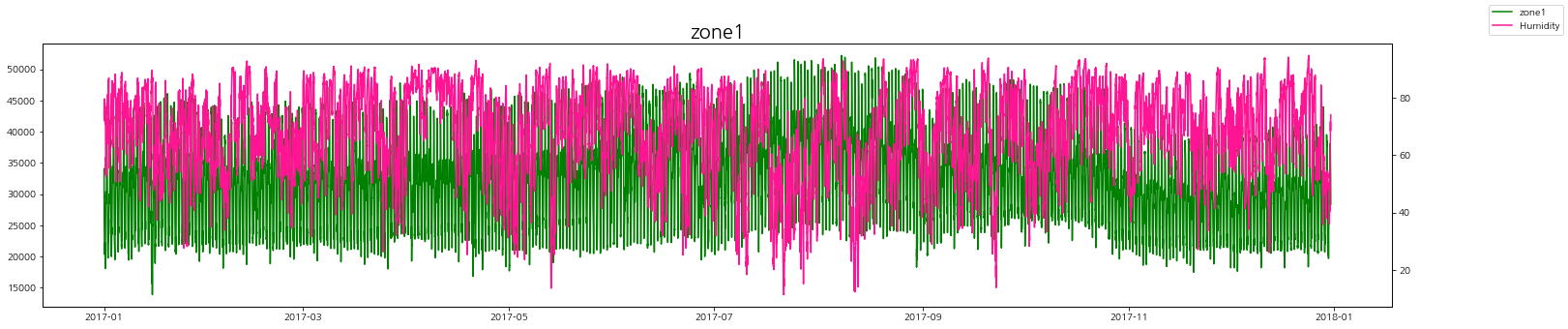
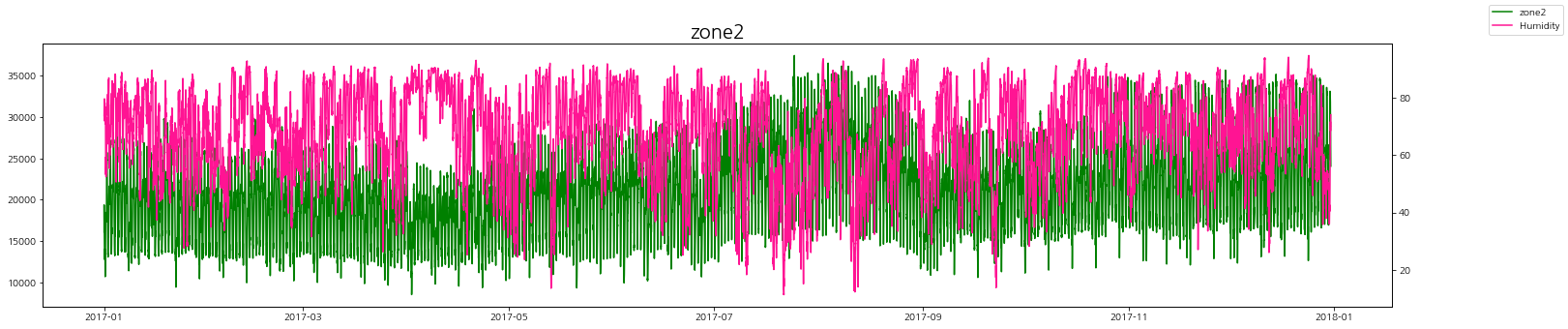
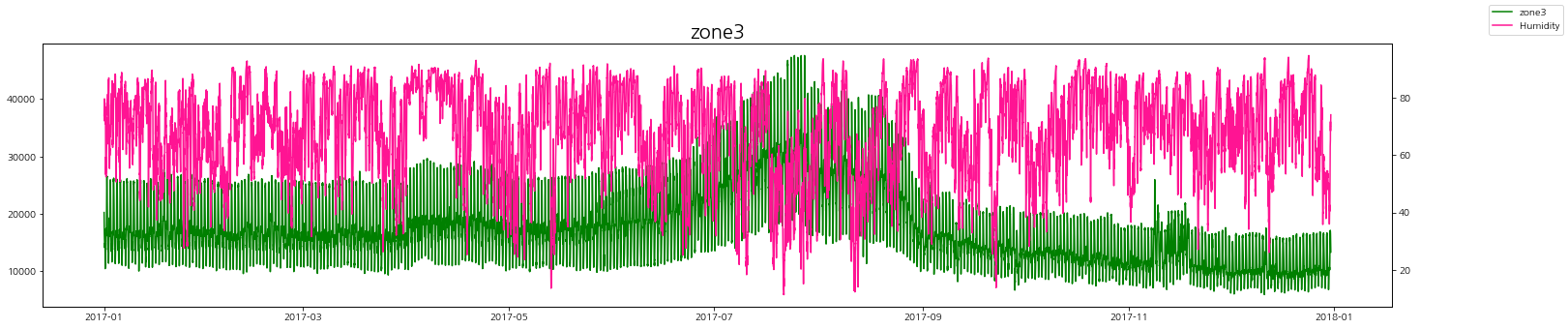
해당 데이터는 시계열 데이터로 시간에 흐름에 따른 zone별 발전량을 시각화해보자.
태영열 발전이라 여름철 전력 발전량이 많은 것을 볼 수 있다.

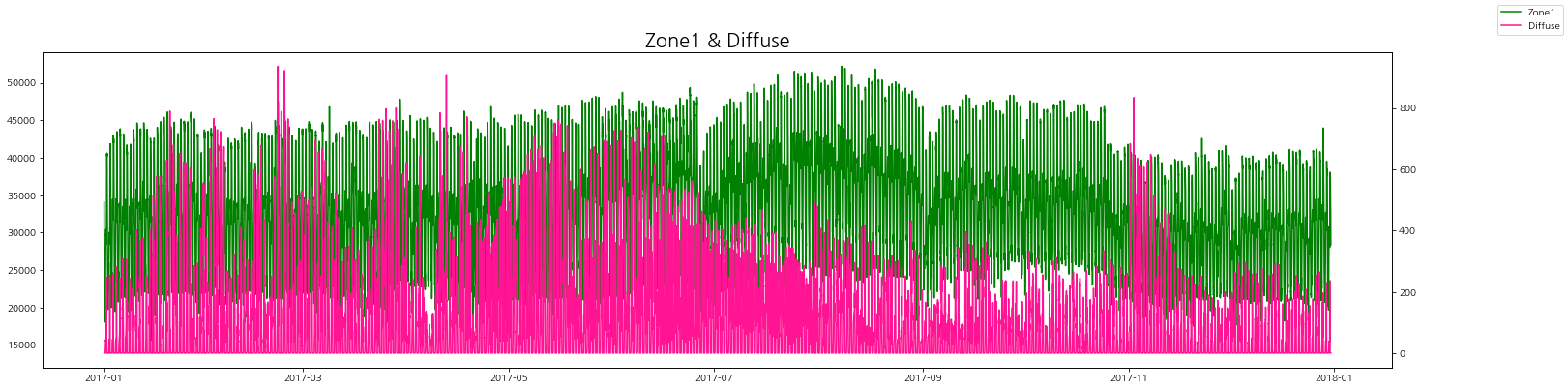
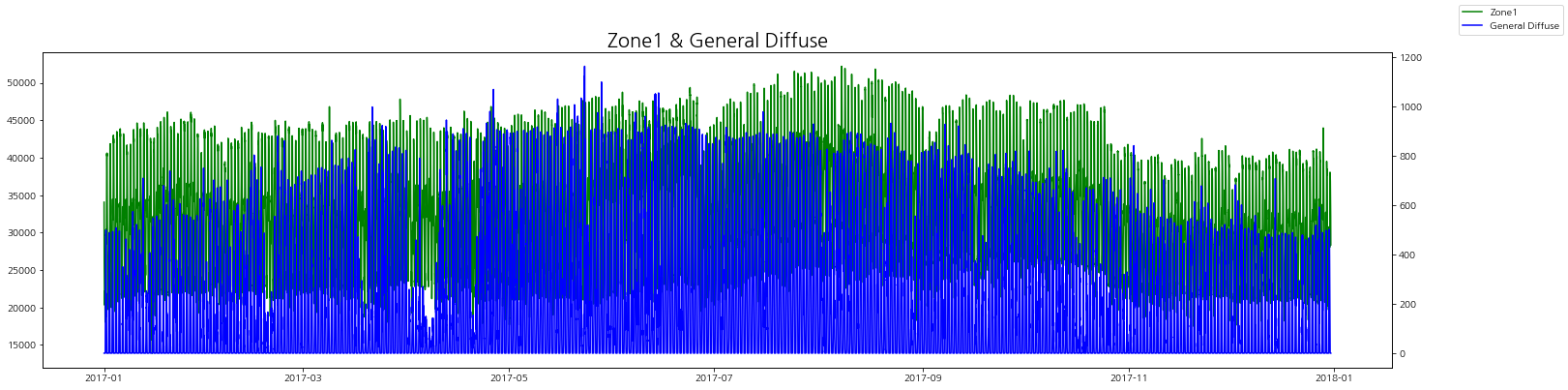
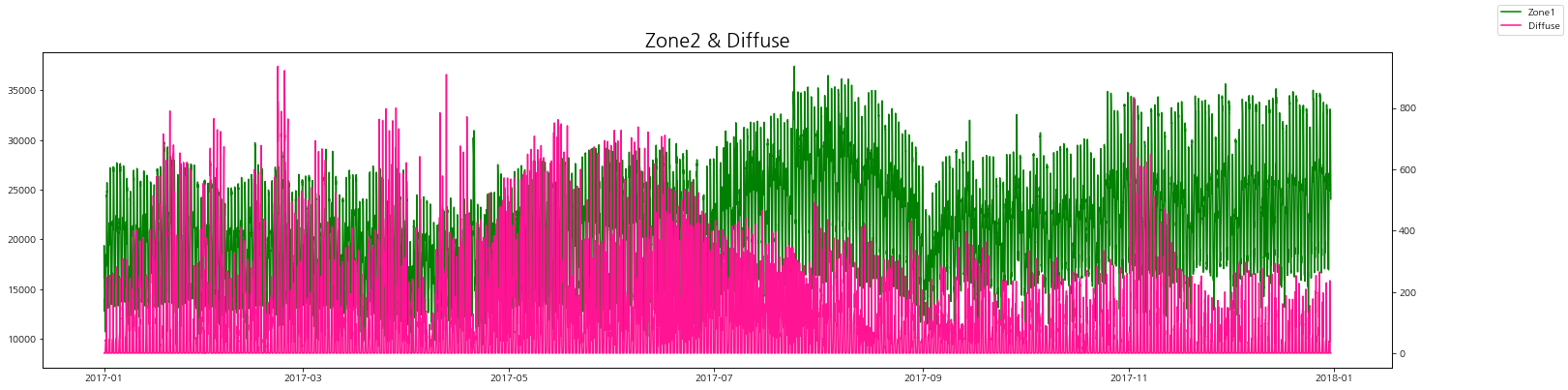
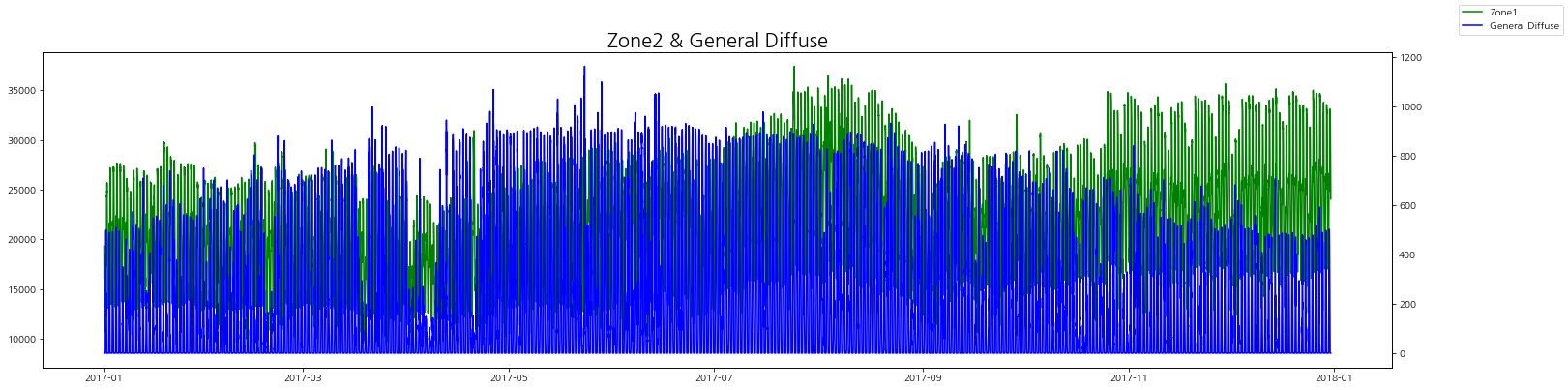
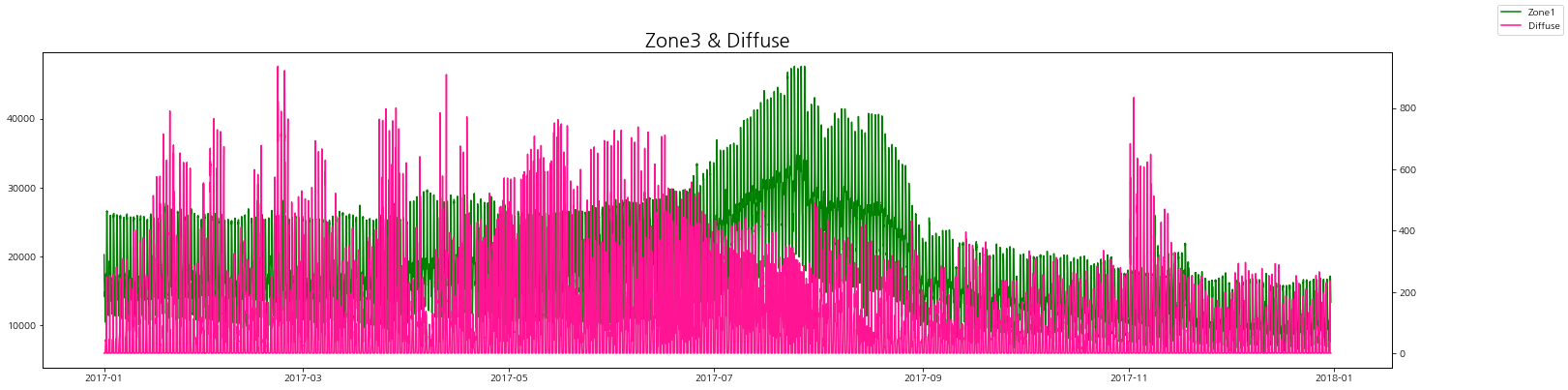
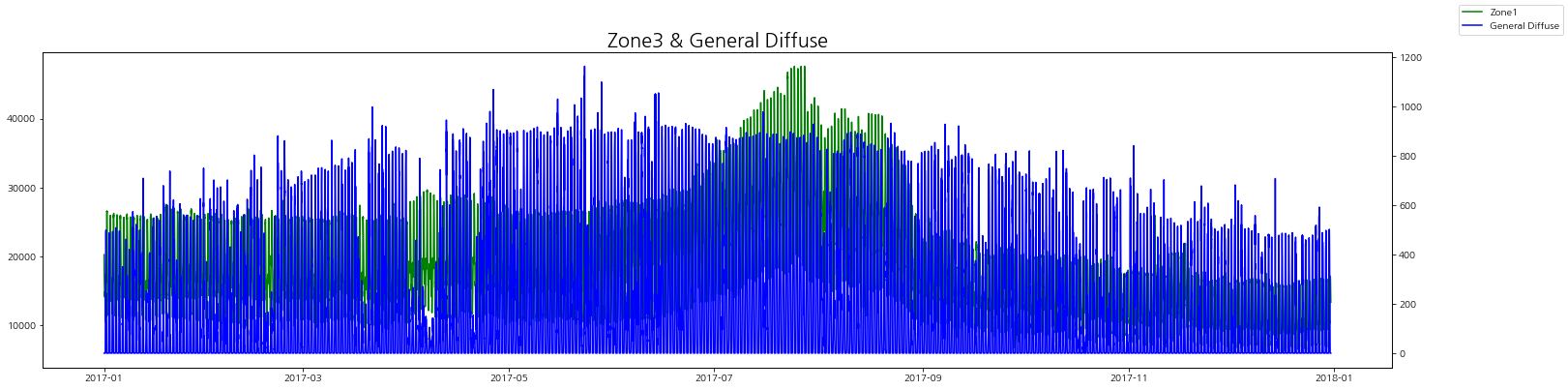
zone별 발전량과 발산량을 그래프로 비교해보자.
zone별로 보았을 때 발산량(실제)이 낮을 때 전력 발전량이 증가하는 경향을 볼 수 있다.
그리고 일반 발산량이랑은 상관 관계는 그래프로는 잘 인식이 되지 않는다.

zone1

zone2

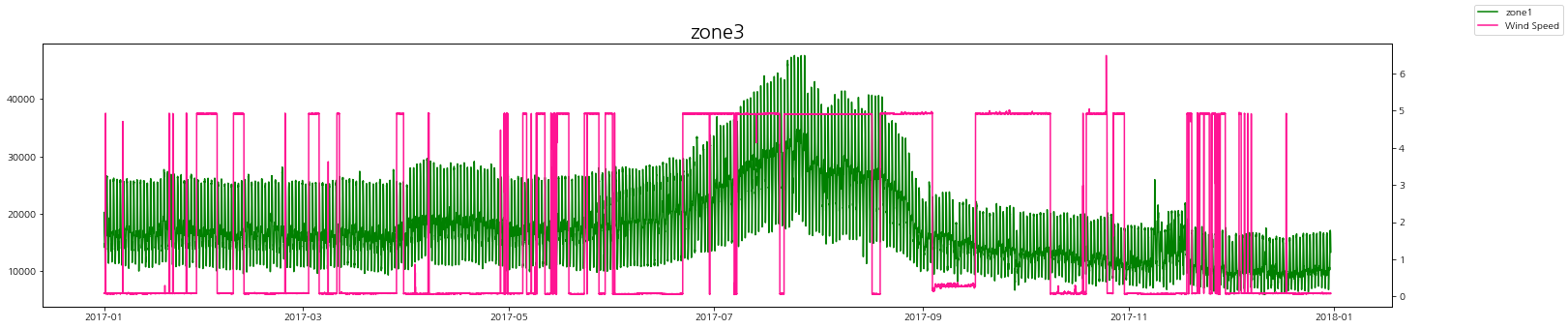
zone3

날짜별 Zone 전력량

월별로 살펴보기 위해 시계열 컬럼에서 월만 분리하여 컬럼을 생성한다.

# 데이터 컬럼명 변경 : 컬럼명이 너무 긴 것은 줄이고
powercomp.columns=['DateTime', 'Temperature', 'Humidity', 'Wind Speed', 'general diffuse flows', 'diffuse flows', 'zone1', 'zone2', 'zone3', 'month']

# 데이터 컬럼 순서 변경
powercomp = powercomp[['DateTime',  'month', 'Temperature', 'Humidity', 'Wind Speed', 'general diffuse flows', 'diffuse flows', 'zone1', 'zone2', 'zone3']]

월별로 zone의 발전량 평균을 보면 다음과 같다.
zone별로 발전량의 최대치가 조금씩 다른 것을 볼 수 있다.

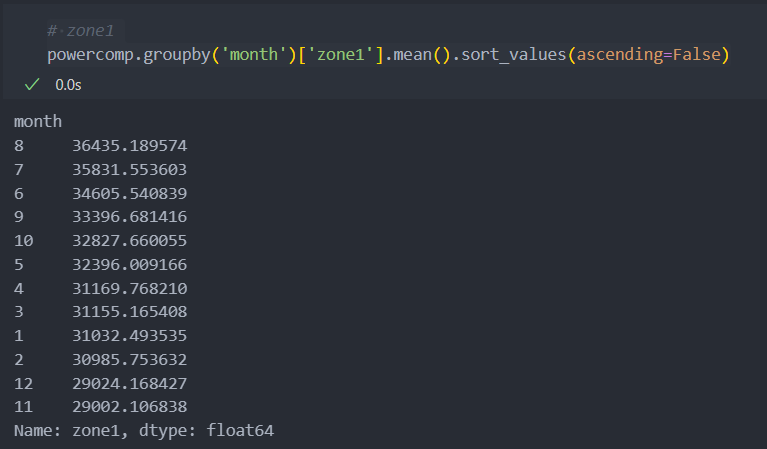
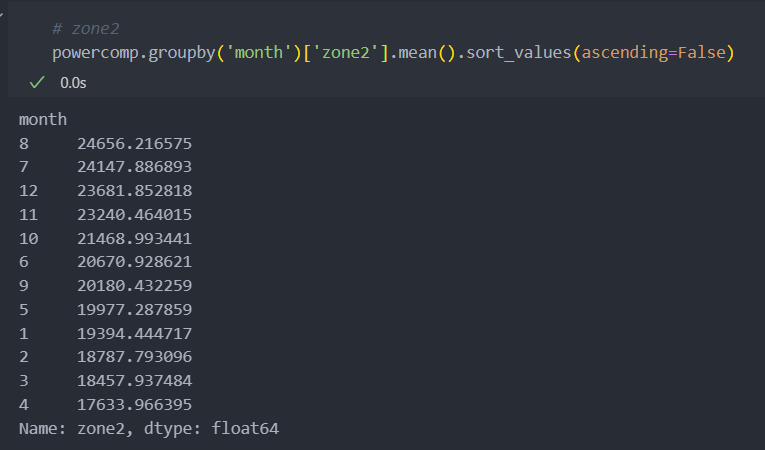
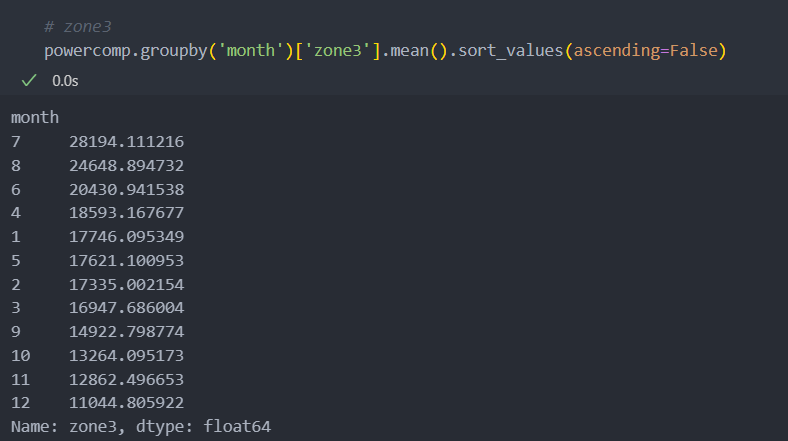
조금 범위를 줄여서 일별 어느 시간대가 가장 많은 발전량을 가지는지 살펴보자.
먼저 '시간' 컬럼을 시계열 컬럼에서 새롭게 만든다.

powercomp['hour'] = powercomp['DateTime'].dt.hour

zone별 어느 시간대가 발전량이 많은지 보자.
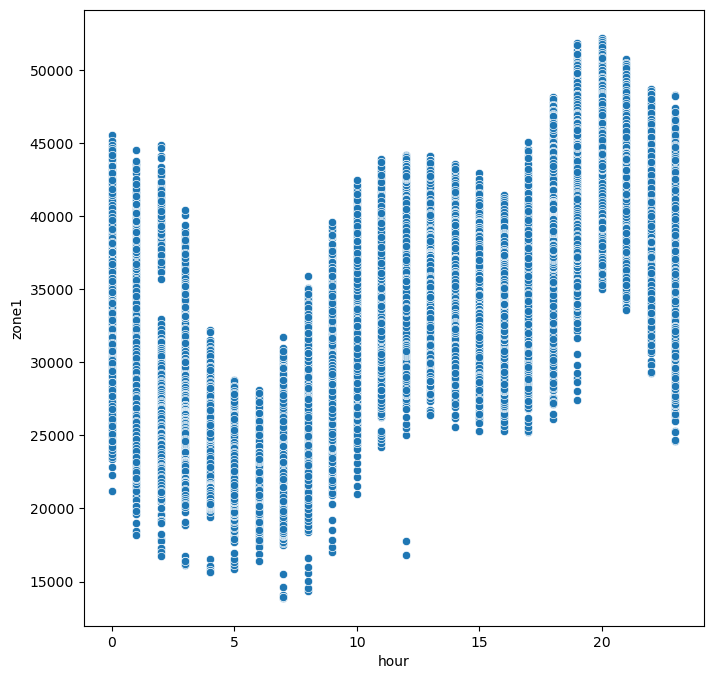
의외로 저녁 시간대에 모든 zone에서 발전량이 제일 많은 것을 볼 수 있다.

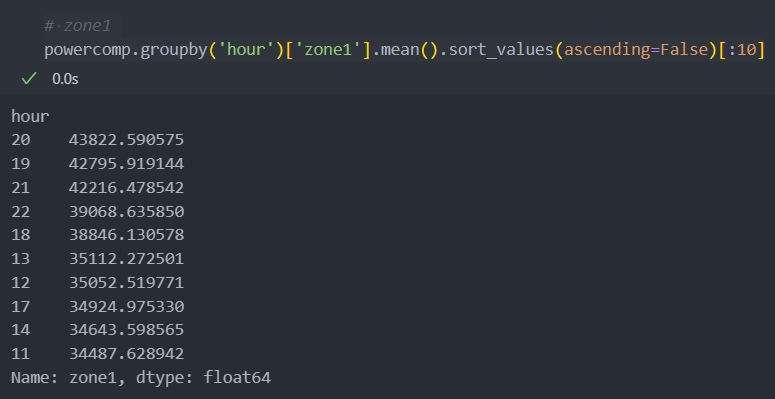
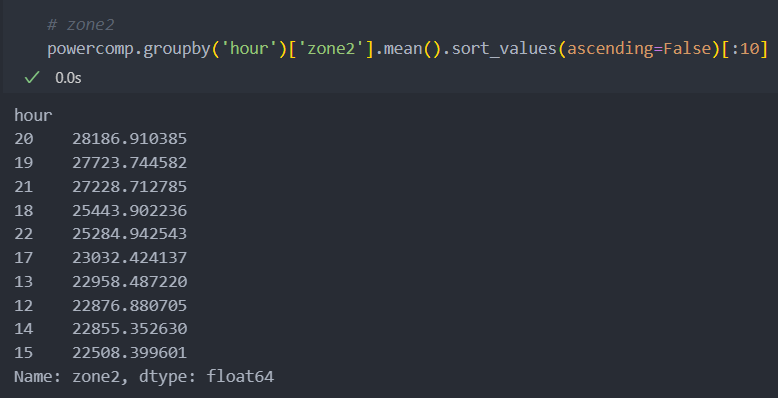
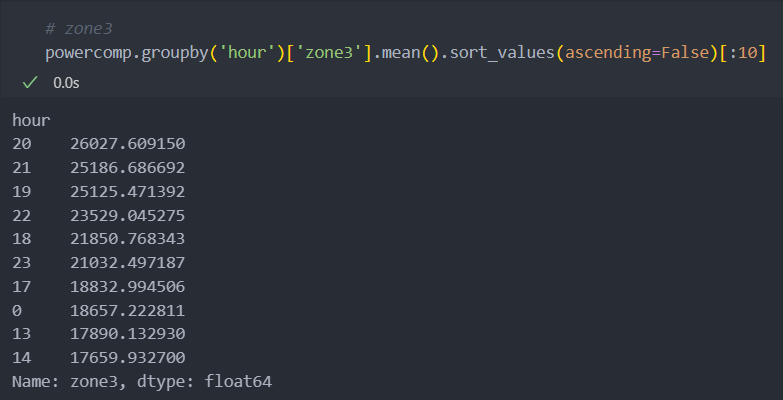
월로 보았을 때, 7, 8월이 가장 전력량이 많았었다.
그래서 중간 지점인 8월 1일의 시간대별 발전량의 흐름을 그래프로 그려보자.
zone 모두가 새벽에는 전력량이 낮고 낮에는 전력량이 많아지다가 저녁에는 다시 한 번 많아지는 현상을 볼 수 있다.

plt.figure(figsize=(25, 12))

plt.subplot(311)
plt.title('zone1')
plt.plot(zone8_1['DateTime'], zone8_1['zone1'], label='zone1')

plt.subplot(312)
plt.title('zone2')
plt.plot(zone8_1['DateTime'], zone8_1['zone2'], label='zone2')

plt.subplot(313)
plt.title('zone3')
plt.plot(zone8_1['DateTime'], zone8_1['zone3'], label='zone3')

plt.show()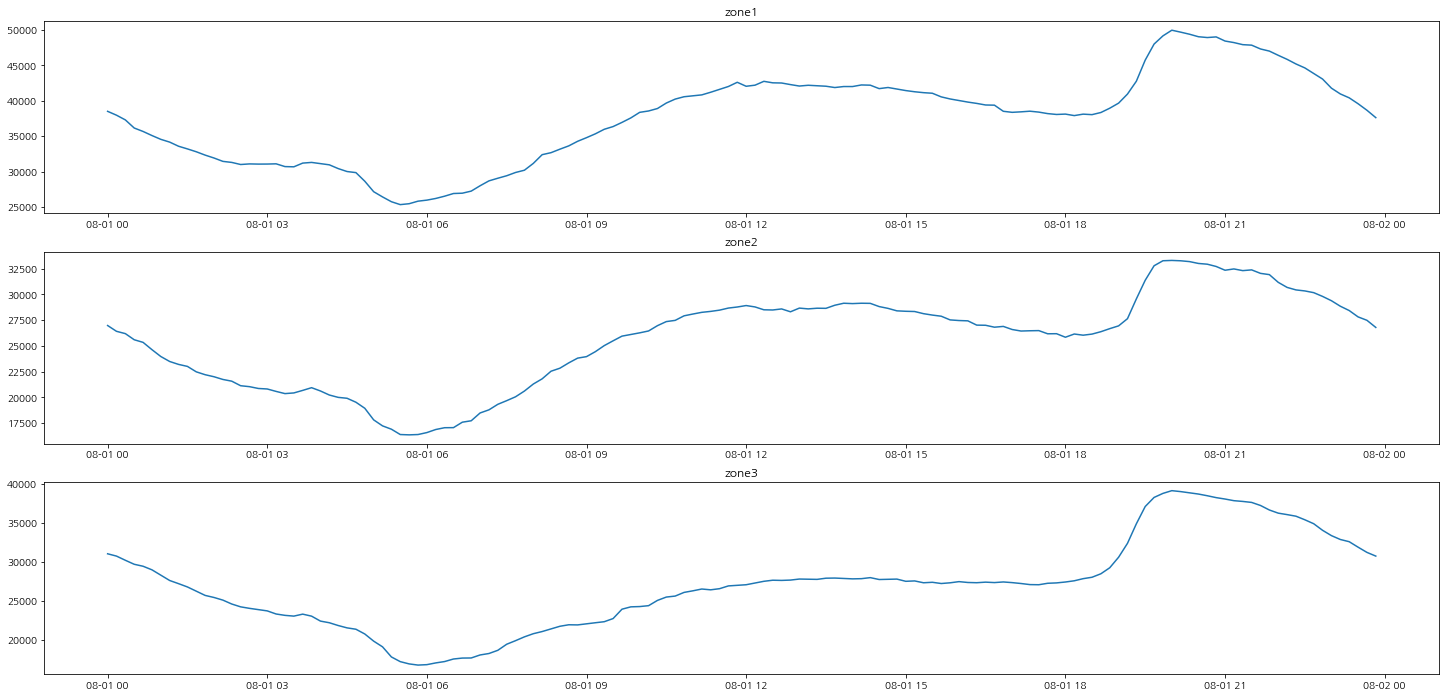

그럼 여름철이 아니라 겨울철에도 한 번 보자.
겨울철에도 발전량의 시간대별 흐름은 비슷한 경향을 보이는 것을 확인할 수 있다.

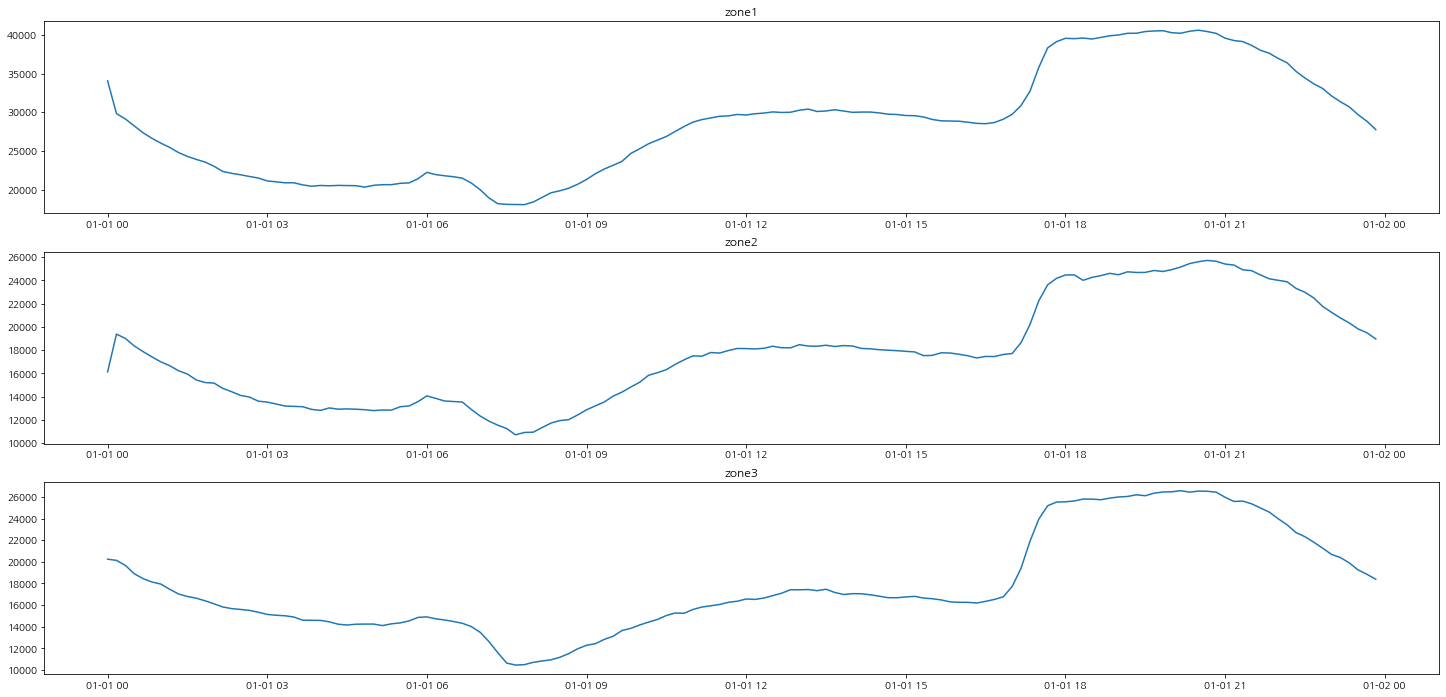
시간 변수가 발전량을 예측하는데 중요한 특징이 될 것이라 예측이 된다.

상관관계 분석

온도와 발전량

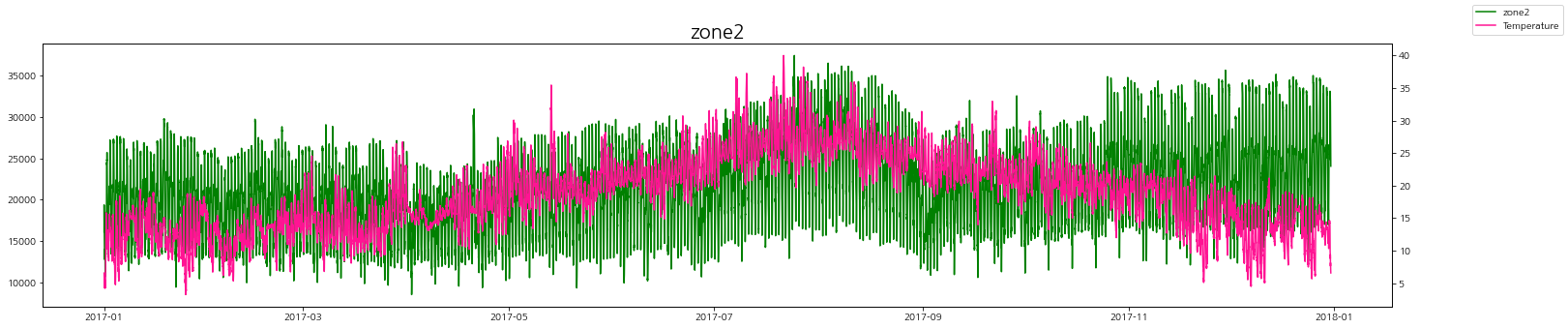
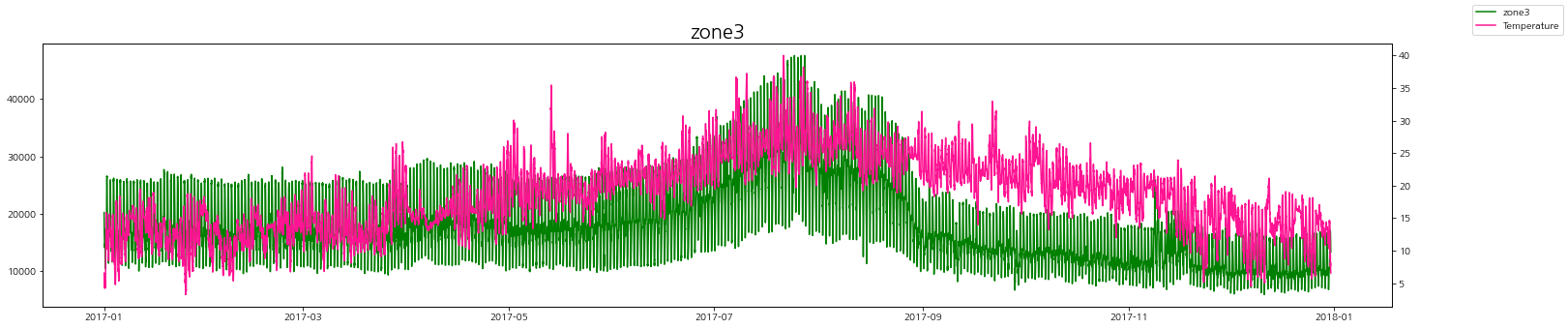
온도에 따른 zone별 발전량을 그래프로 살펴보자.
zone별로 온도가 높을 때 발전량도 같이 증가하는 경향을 볼 수 있다.

fig, ax = plt.subplots()
ax.plot(powercomp['DateTime'], powercomp['zone1'], color='green', label='zone1')

ax_1 = ax.twinx()
ax_1.plot(powercomp['DateTime'], powercomp['Temperature'], color='deeppink', label='Temperature')

fig.legend()
plt.title('zone1', fontsize=20)
plt.gcf().set_size_inches(25, 5)
plt.show()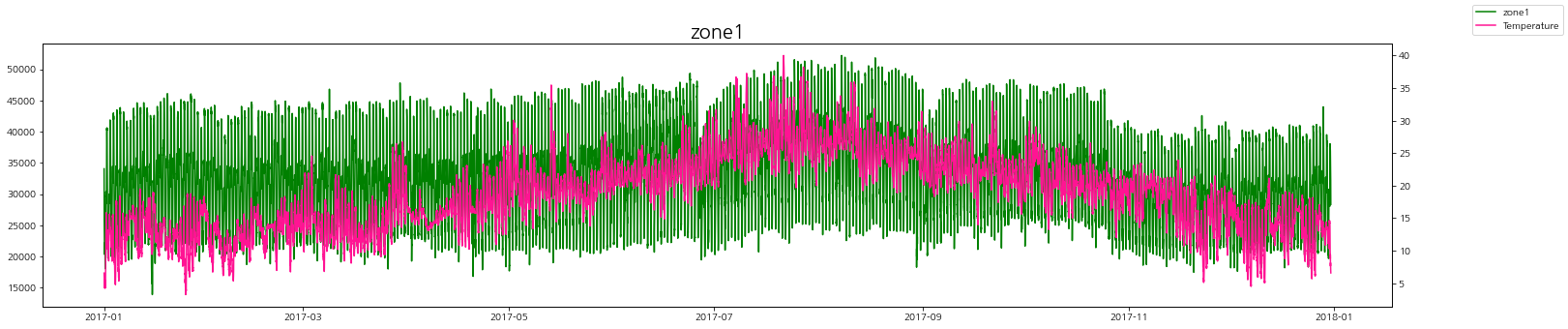

피어슨 상관계수

온도와 zone별 피어슨 상관계수를 산점도 그래프로 알아보자.
피어슨 상관계수란 두 변수 간의 선형 상관 관계를 계량화한 수치로 -1(음의 상관관계)에서 1(양의 상관관계) 사이의 값을 가지며, 절대값 1에 가까울수록 상관 관계가 높으며 0에 가까울 수록 상관 관계가 없다고 판단한다.

scipy모듈의 stats.pearsonr
· 0.0 <= |r| < 0.2 : 상관관계가 없다. = 선형의 관계가 없다.
· 0.2 <= |r| < 0.4 : 약한 상관관계가 있다.
· 0.4 <= |r| < 0.6 : 보통의 상관관계가 있다.
· 0.6 <= |r| < 0.8 : 강한 (높은) 상관관계가 있다.
· 0.8 <= |r| <= 1.0 : 매우 강한 (매우 높은) 상관관계가 있다.

sns.scatterplot(x=powercomp['Temperature'], y=powercomp['zone1'])
plt.gcf().set_size_inches(8, 8)
plt.title('피어슨 상관 계수(온도 VS zone1) : ' + f"{stats.pearsonr(x=powercomp['Temperature'], y=powercomp['zone1'])[0]:.3f}", fontsize=20)
plt.show()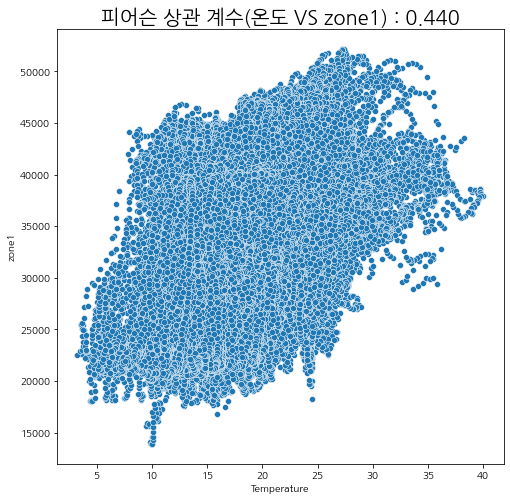

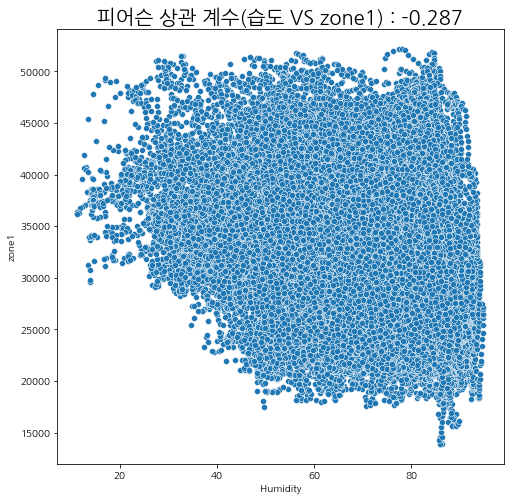
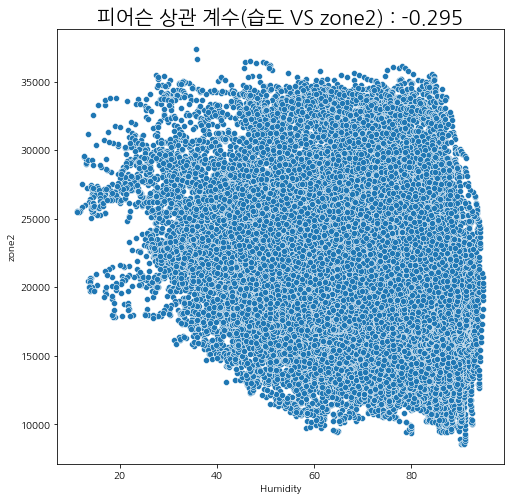
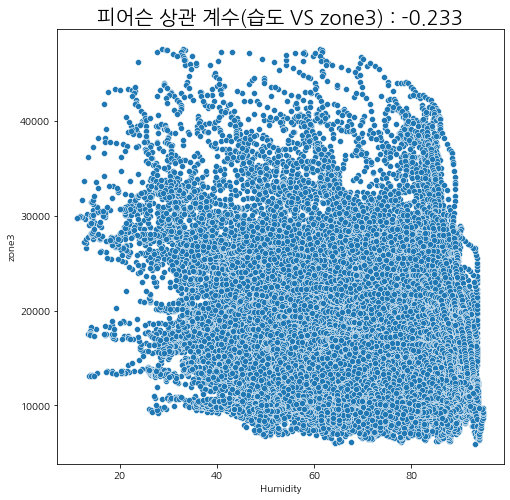
습도와 발전량

습도에 따른 zone별 발전량 상관관계를 살펴보자.
상관관계가 있다고 말하기는 어려워 보인다.
그나마 여름철에 습도가 내려갔을 때 발전량이 조금 올라가는 것을 볼 수 있다.

피어슨 상관계수

산점도와 피어슨 상관관계를 살펴보아도 유의미한 상관성이 보이지는 않는다.

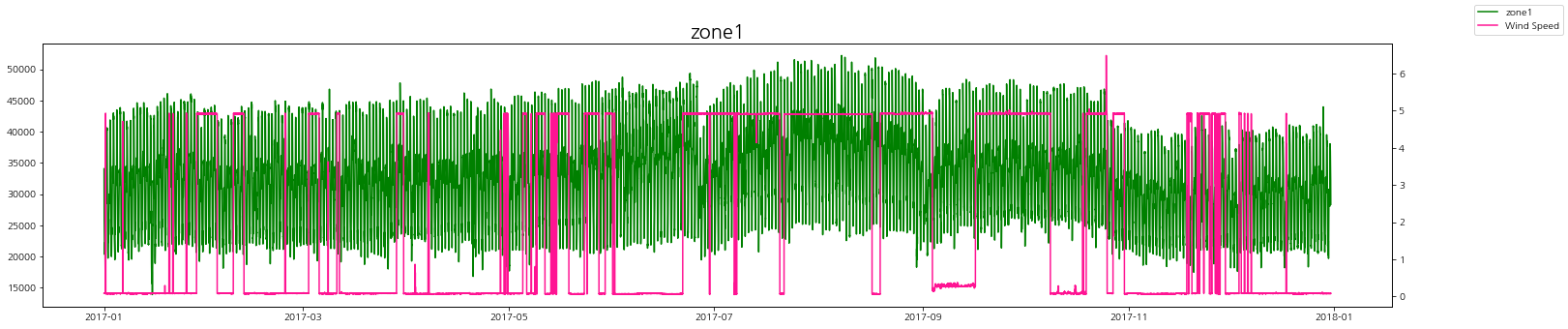
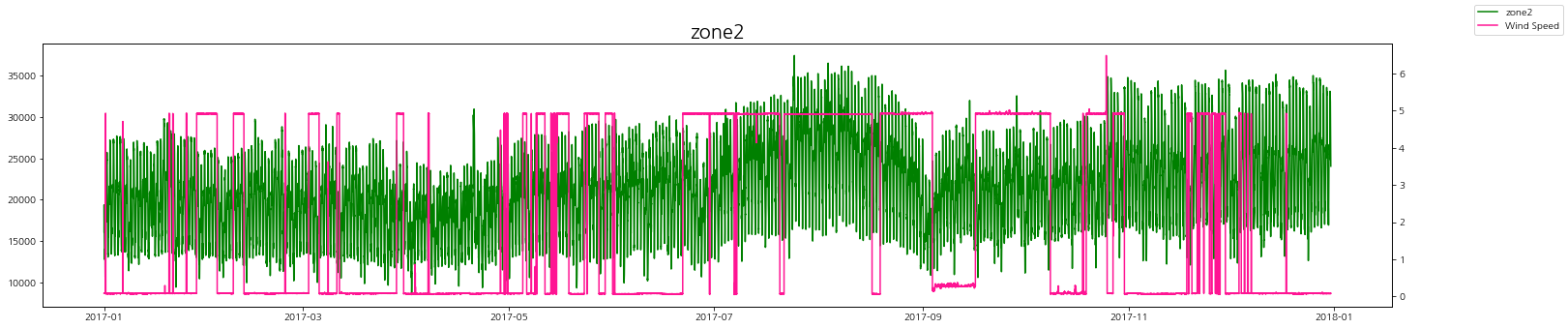
풍속과 발전량

풍속에 따른 zone별 발전량 상관관계를 살펴보자.
상관관계가 있다고 말하기는 어려워 보인다.
하지만 바람이 일정할 때, 발전량이 꾸준히 낮거나 꾸준히 높게 유지가 되는 것을 볼 수 있다.

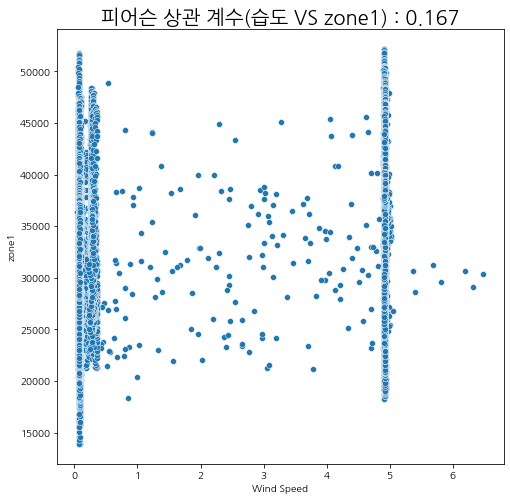
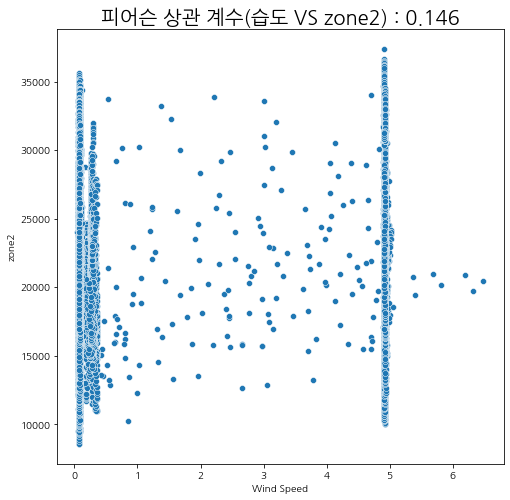
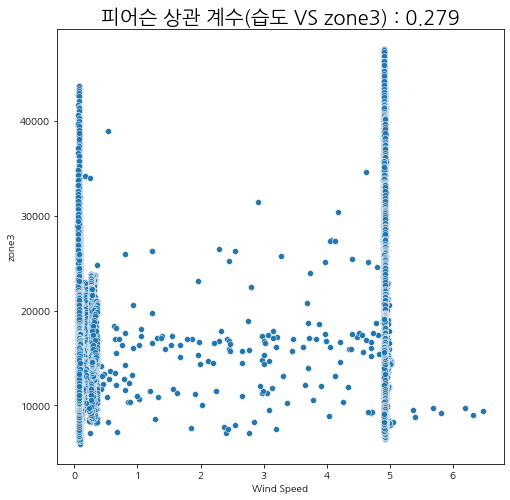
피어슨 상관계수

산점도와 피어슨 상관관계를 살펴보아도 유의미한 상관성이 보이지는 않는다.

모든 변수들 간 상관관계

DataFrame.corr()

변수들 간의 상관관계 계수

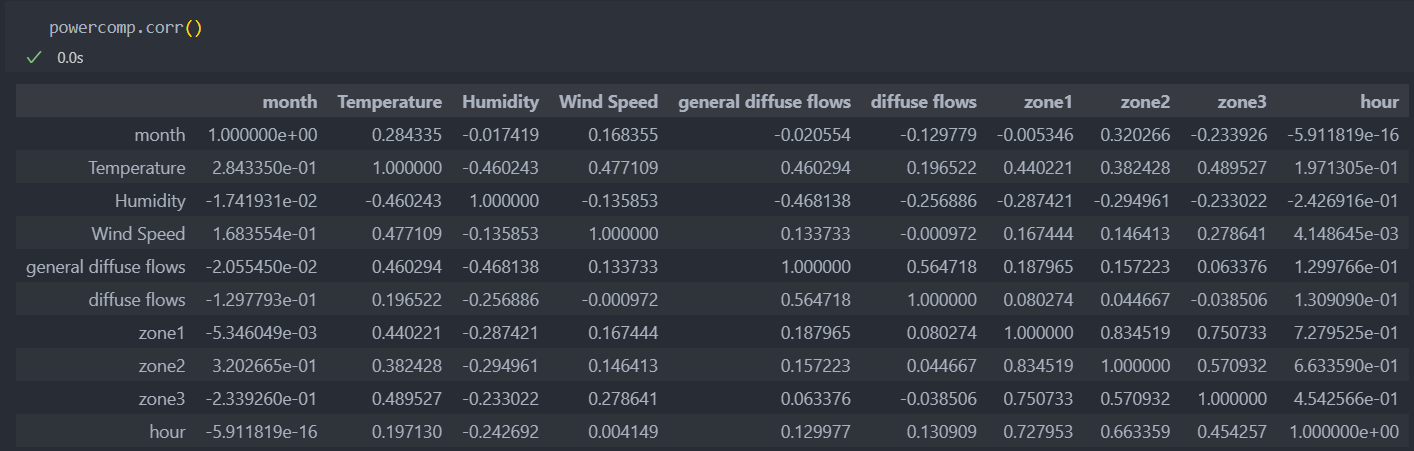
온도 및 습도를 포함하여 다른 변수들과 zone의 상관관계를 pairplot 그래프로 보자.
Temperature는 데이터의 분포는 가운데로 모여있으면서 꼭지점이 2개로 보인다.
Humidity는 데이터의 분포는 오른쪽으로 치우쳐져 있다.
Wind Speed은 0 아니면 5에 몰려있는 분포를 가진다.
일반적인 전력 발산량이 높으면 실제 전력 발산량도 높아진다.

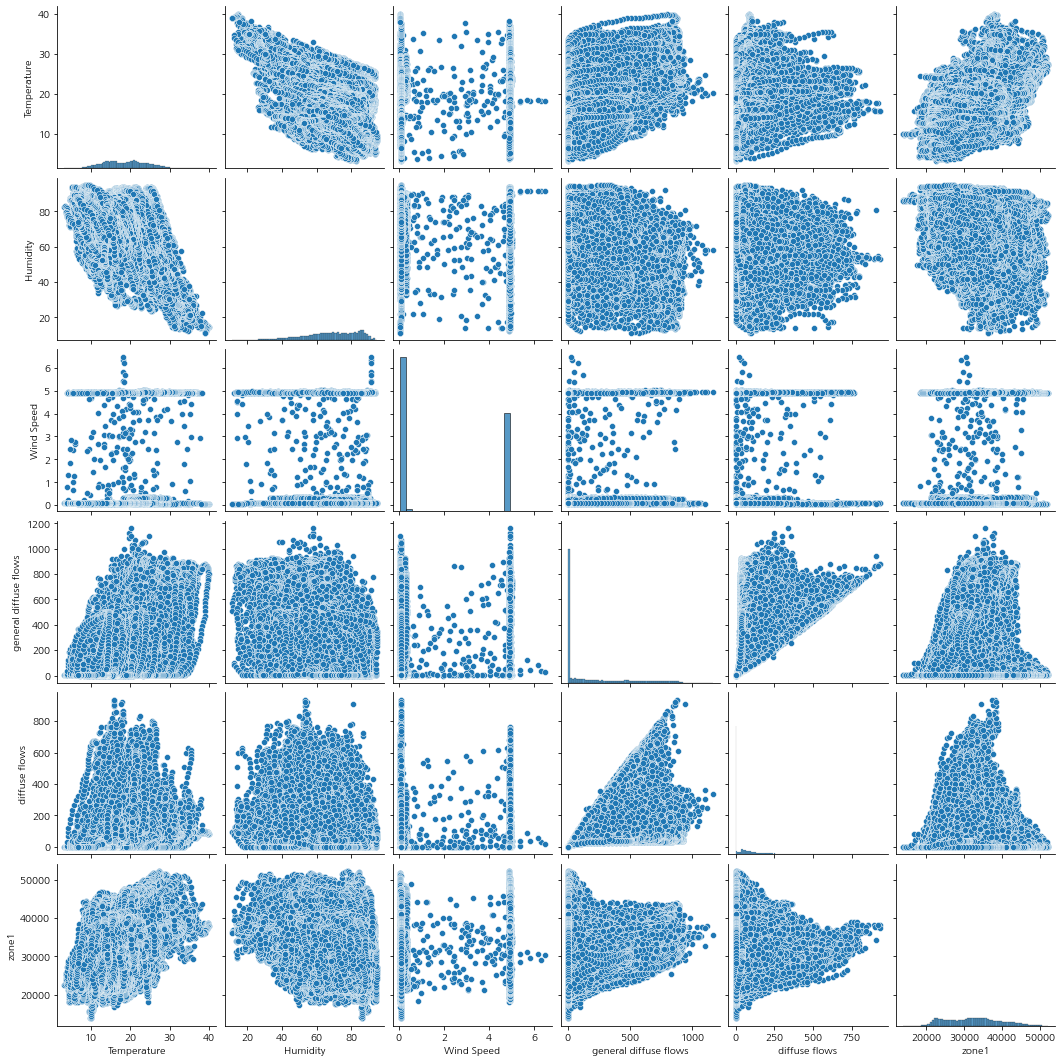
그리고 히트맵을 통해서 모든 변수에 대한 상관 관계를 그려보자.

모델링

모델 선정

참조 : 특징 선택

특징 대비 샘플 수가 많고, 특징을 모두 연속형으로 되어 있다.

사용할 모델

• kNN model
• RandomForestRegressor model
• LightGBM model

특징 선택

• 특징 선택 : 3 ~ 10개 사용
• 통계량 : F 통계량 / 연속형 변수들이며 회귀 -> f_regression 사용

라벨은 zone1을 선택하였다.
zone별로 서로 상관성을 띄고 있어고 전력 생산량이 가장 많아서 대표로 선택하였다.

from sklearn.neighbors import KNeighborsRegressor as KNN
from sklearn.ensemble import RandomForestRegressor as RFR
from lightgbm import LGBMRegressor as LGB

from sklearn.model_selection import ParameterGrid
from sklearn.metrics import mean_absolute_error as MAE
from sklearn import metrics

from sklearn.model_selection import train_test_split
from sklearn.feature_selection import *

하이퍼 파라미터 튜닝

하이퍼 파라미터 튜닝

# 하이퍼 파라미터를 담을 변수 생성
param_grid = dict()

# 모델별 하이퍼 파라미터 그리드 생성
param_grid_for_knn = ParameterGrid({
                                    'n_neighbors':[1, 3, 5, 7],
                                    'metric':['euclidean', 'cosine']
})
param_grid_for_RFR = ParameterGrid({
                                    'max_depth':[2, 5, 10, 15],
                                    'n_estimators':[100, 200, 400],
                                    'max_samples':[0.5, 0.6, 0.7, None]
})
param_grid_for_LGB = ParameterGrid({
                                    'max_depth':[2, 3, 4, 5],
                                    'n_estimators':[100, 200, 400],
                                    'learning_rate':[0.05, 0.1, 0.15]
})

param_grid[KNN] = param_grid_for_knn
param_grid[RFR] = param_grid_for_RFR
param_grid[LGB] = param_grid_for_LGB

학습 진행

모델별/튜닝별 반복 횟수는 460회

# max iter 계산 : 모델/파라미터별로 모든 iter = 460
max_iter_num = 0
for k in range(6, 1, -1): # 특성 개수 선택
    for m in param_grid.keys(): # 모델별
        for p in param_grid[m]:
            max_iter_num += 1

print(max_iter_num)

결과:
460

학습을 진행해보자.

best_score = 1e9
iteration_num = 0
knn_list = []
rfr_list = []
lgb_list = []

for k in range(6, 1, -1): # 메모리 부담을 줄이기 위한
    selector = SelectKBest(f_regression, k=k).fit(train_x, train_y)
    selected_features = train_x.columns[selector.get_support()]

    # 선택한 특징으로 학습 진행하기 위한 : 특징 개수를 줄여나가며 메모리 부담도 줄인다.
    train_x = train_x[selected_features]
    test_x = test_x[selected_features]

    for m in param_grid.keys():
        for p in param_grid[m]:
            model = m(**p).fit(train_x.values, train_y.values)
            pred = model.predict(test_x.values)
            score = MAE(test_y.values, pred)

            if score < best_score:
                best_score = score
                best_model = m
                best_parameter = p
                best_features = selected_features
                
            if m == KNN:
                knn_list.append(score)
            elif m == RFR:
                rfr_list.append(score)
            elif m == LGB:
                lgb_list.append(score)
            
            iteration_num += 1

            print(f'iter_num-{iteration_num}/{max_iter_num} => score : {score:.3f}, best score : {best_score:.3f}')

best score, model, param, features를 보자.
모델의 하이퍼 파라미터가 정해지면 좀 더 세분화해서 하이퍼 파라미터 튜닝의 단계를 몇 번 더 거치는 것이 좋다.

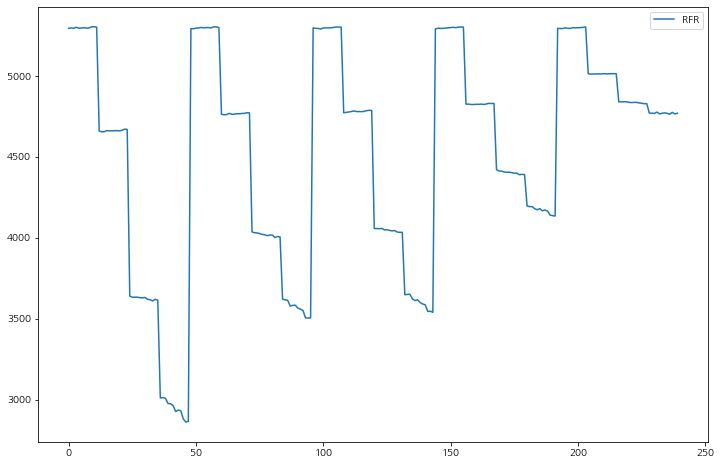
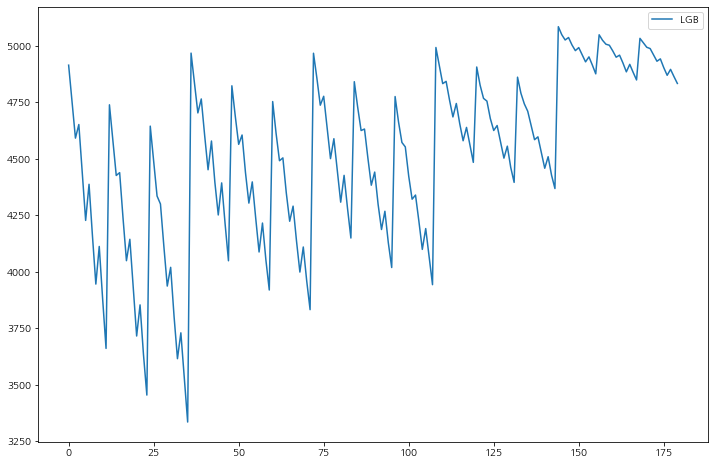
각 모델별로 특성의 개수가 줄어들수록(6개에서 2개까지) 성능이 나빠지는 것을 볼 수 있다.
큰 꼭지점에 모델별로 5개씩 있고,
선택된 RandomForestRegressor 경우 점점 성능이 좋아지다가 다시 안 좋아지는 형식은데 max_depth, n_estimators가 깊고 많을 수록 성능이 좋아진다.
MAE는 수치가 낮을 수록 모델의 성능이 좋다.

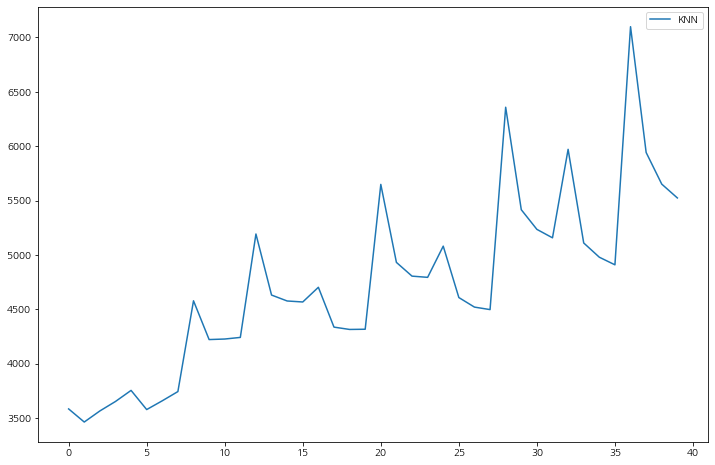
최종 모델 선택

다시 학습/평가 데이터와 data와 label데이터로 분리한다.

# 데이터 다시 만들기 : 학습을 진행하며 메모리 부담을 줄이기 위해서 컬럼을 줄이면서 학습을 하였기 때문.(hour 추가)
X = powercomp[['month', 'hour', 'Temperature', 'Humidity', 'Wind Speed', 'general diffuse flows', 'diffuse flows']]
Y = powercomp['zone1']

train_x, test_x, train_y, test_y = train_test_split(X, Y)

train_x.shape, train_y.shape, test_x.shape, test_y.shape

선택된 최종 모델로 다시 학습을 시키고 결과를 보자.

# 최종 모델
model = best_model(**best_parameter).fit(train_x, train_y) # 모든 features 넣기

# 예측
pred = model.predict(test_x)

result = pd.DataFrame({
                        'Real Values':test_y,
                        'predicted Values':pred
}).reset_index(drop=True)
result['diff'] = result['Real Values'] - result['predicted Values']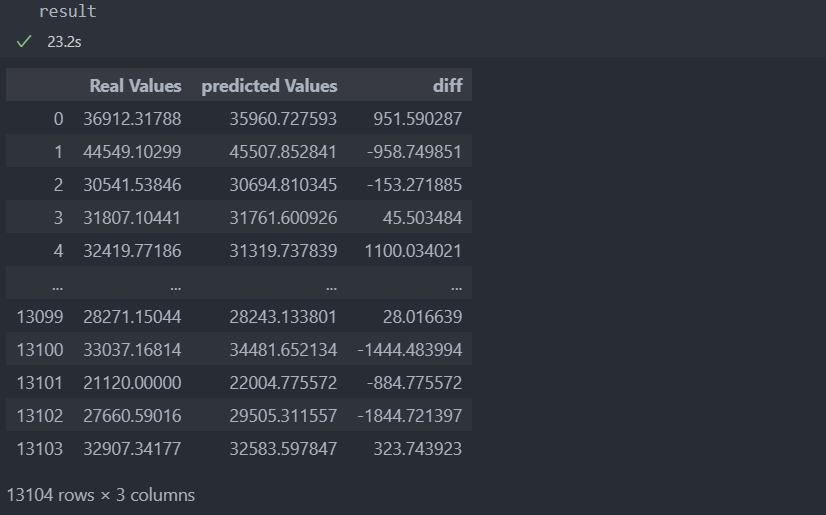

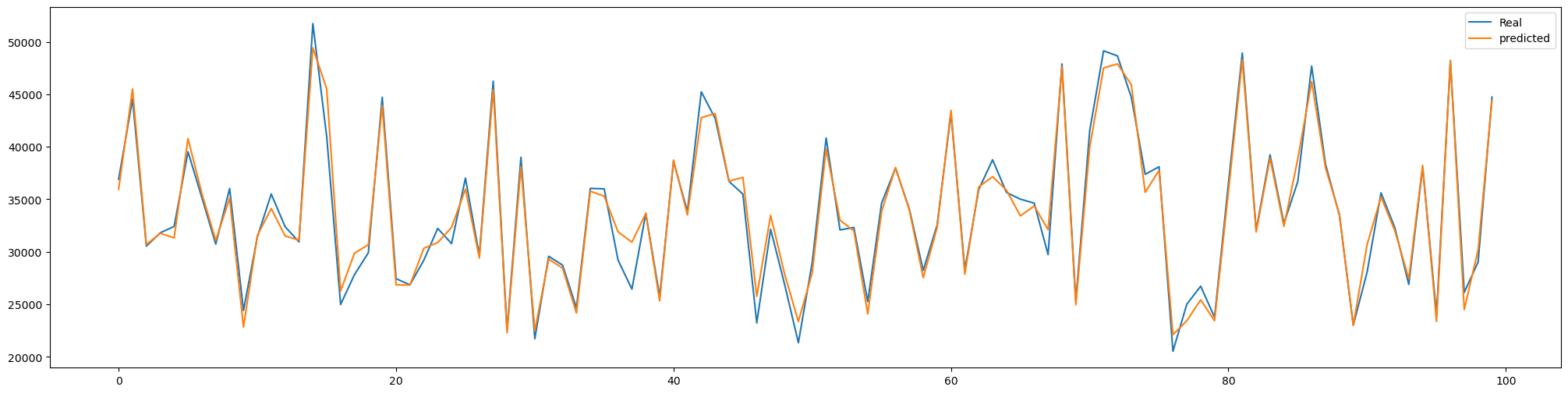
그리고 실제값과 예측값을 그래프로 그려서 예측을 어떻게 했는지 시각화해본다.

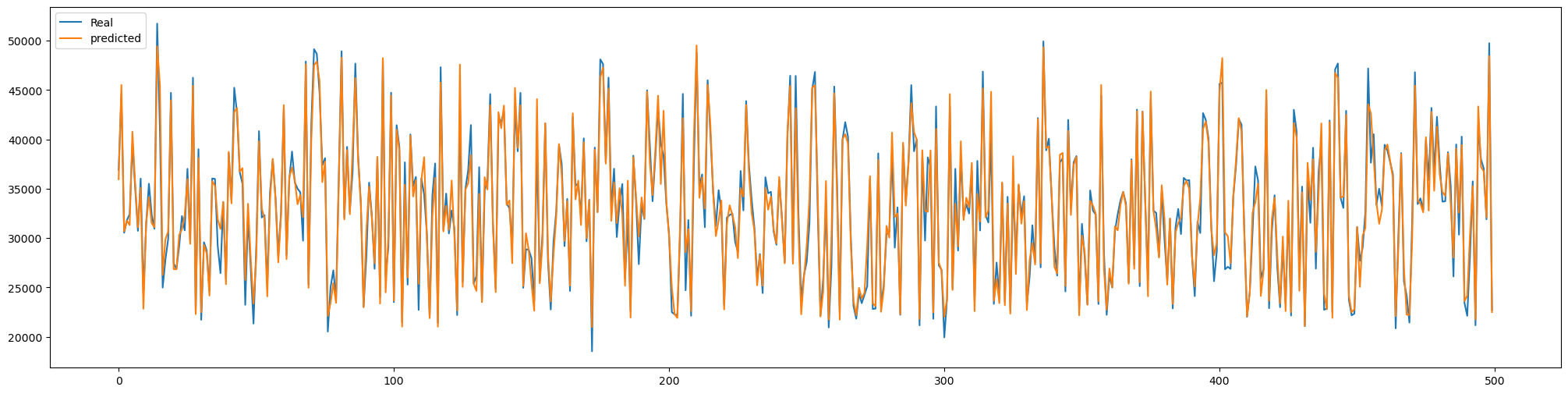
단계를 100으로 줄여서 다시 보자.
예측력이 상당히 좋다는 것이 확인이 된다.

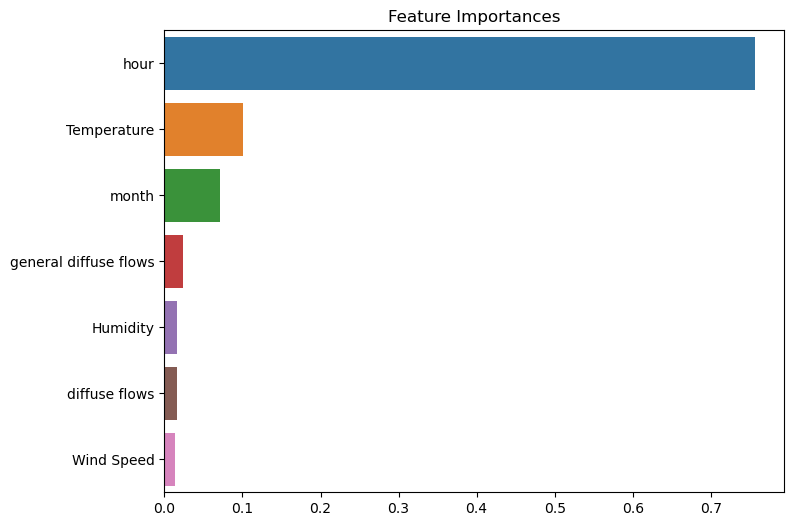
중요 변수 확인

featureimportances
시간대가 75% 정도로 중요한 데이터 역할을 한다.

중요 변수를 그래프로 확인해보자.

시간에 따른 변수의 변화를 보자.

기대효과

일기예보 기상 데이터 실시간 수집 체계 구축 및 발전량 센서 Data 실시간 Server 전송 체계 구축을 통해
일정 주기 간격으로 기상 데이터 인입 및 모델을 통해 발전량 예측 데이터 생성하고 생성된 데이터에 따라 전력 계획안 수립한다.
이로 인해 전력예산 수립으로 인한 운영 비용 절감하여 예산 확보 및 운영 정상화를 기대한다.