
문제 정의
장비 고장 발생하면 전체 공정이 중지가 되어 손해가 발생한다.
고장이 나기 전 사전 이상징후를 포착하고 점검을 통해 고장이 발생하여 미치는 손실을 줄이고자 한다.
진행
소스 코드 및 데이터 : GitHub
데이터 확인
장비의 이상징후를 포착하기 위해 장비의 특정 위치의 충돌 센서 4개(S1~S4)를 설치하였다.
센서 특정 위치에 충돌이 일어나면 최종적으로 충돌 당시의 M(질량)과 V(속도)가 기록된다.
장비에 특정 이상의 충격(M*V)이 가해지면 장비는 정지하게 된다.
- abnormal_features.csv : id별 4개의 센서값과 발생 시간
- abnormal_target.csv : id별 x, y좌표와 M(질량)과 속도(V)가 기록
EDA & 전처리
데이터의 결측치는 없는 것으로 확인 된다.
features의 데이터들은 시간에 따른 값(센서)의 수치들을 담고 있다.
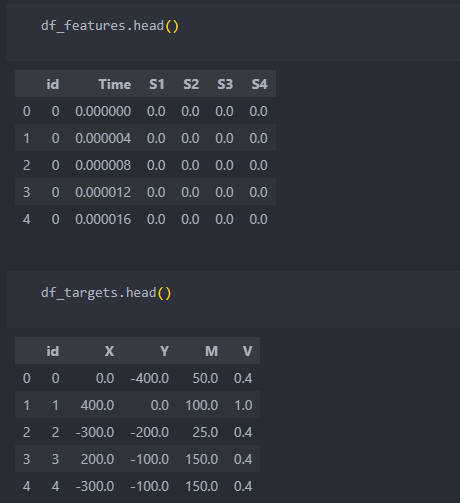
모든 id별 S1의 시간에 따른 평균적 수치는 다음과 같이 나타난다.
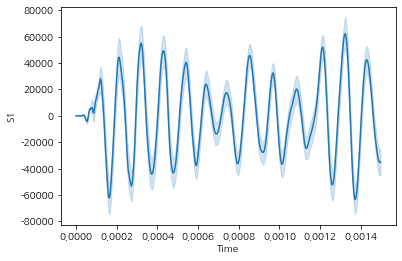
id 중 하나를 골라서 흐름을 보면 아래와 같이 수치가 나타난다.
id별 수치를 가지고 진행하기에는 어려움이 있기에 각 id별 평균적인 수치를 바탕으로 진행을 하도록 한다.
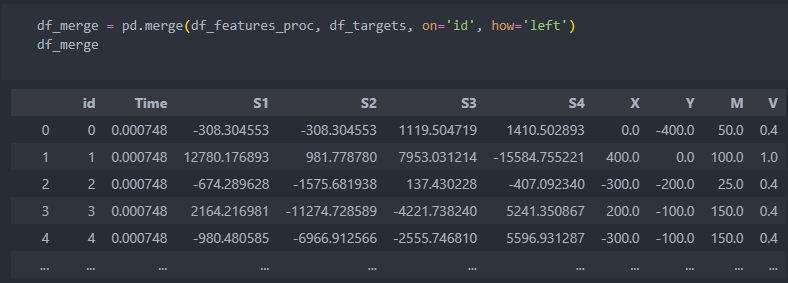
merge
먼저 features를 id별로 수치들의 평균값으로 통합시킨 후,
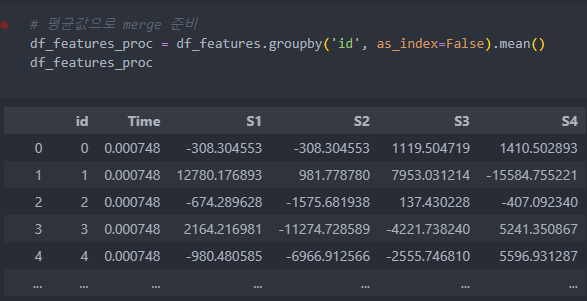
id를 기준으로 통합시키고, 필요가 없을 것이라 판단되는 컬럼들은 삭제를 시킨다.
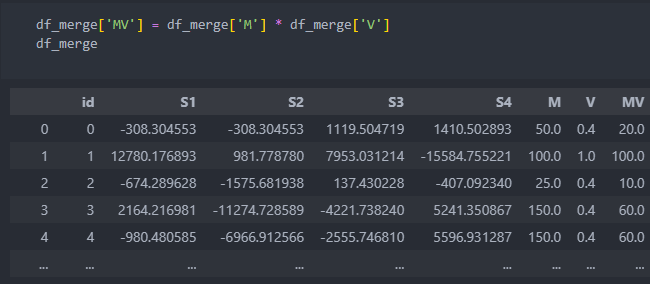
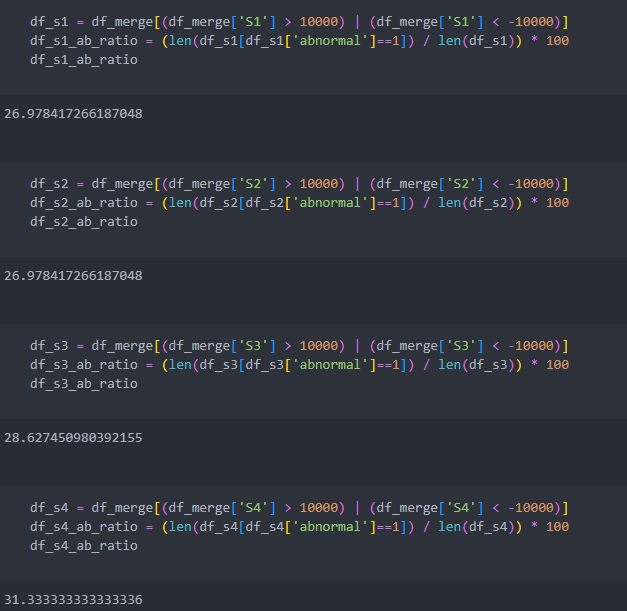
이상 판단을 할 컬럼은 주어지지 않았기에, 질량과 속도를 나타내는 컬럼의 곱을 구하고 평균치에서 일정 이상의 범위를 벗어나는 수치들을 이상치라고 판단하고 진행한다.
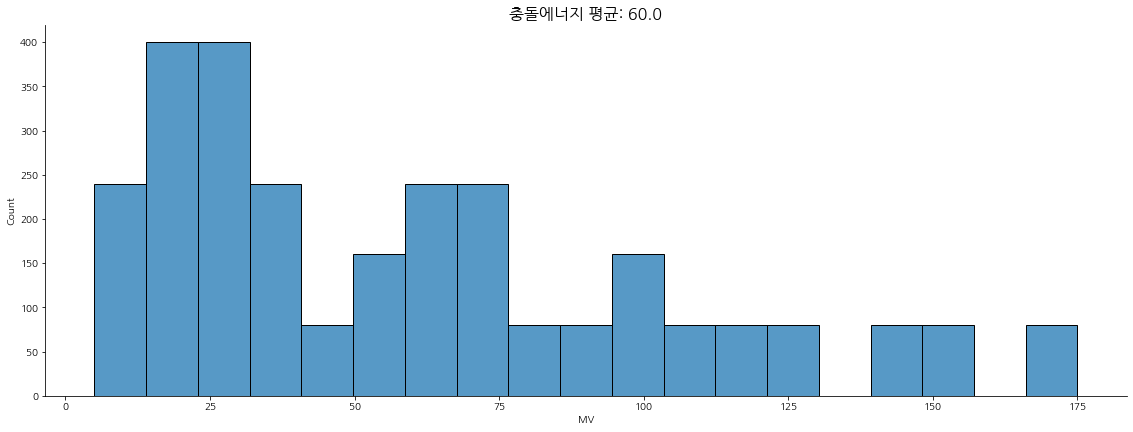
이상치 진단
이상치는 '충돌에너지'라고 표현한 'MV'의 평균에서 표준편차의 2배가 벗어나는 수치들을 이상치라고 라벨을 부여한다.
그리고 이상치는 전체의 약 6%를 차지하고 있다.
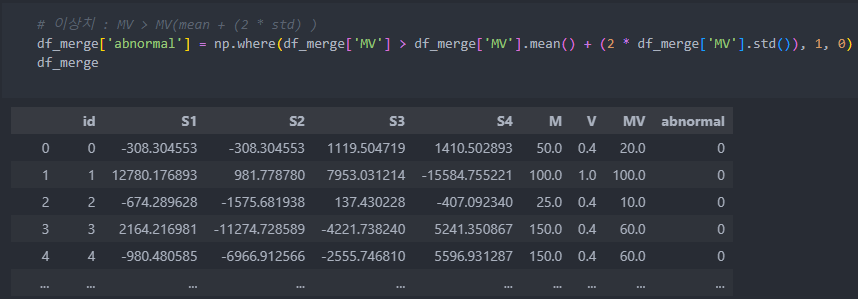

그리고 각 센서들의 이상치라고 판단한 것과 아닌 것의 차이를 보면 아래와 같다.
1, 2의 센서에 비해서 3, 4의 센서 이상치의 평균이 이상치가 아닌 것들보다 차이를 크게 보인다.
이상치를 판단하는 것에 있어서 3, 4의 센서가 이상치를 판단하는데 더 큰 영향을 미칠 것이라 예상이 된다.
# 평균값 비교
print('S1 |', 'abnormal :', df_merge[df_merge['abnormal']==1]['S1'].mean(), '| normal :', df_merge[df_merge['abnormal']==0]['S1'].mean())
print('S2 |', 'abnormal :', df_merge[df_merge['abnormal']==1]['S2'].mean(), '| normal :', df_merge[df_merge['abnormal']==0]['S2'].mean())
print('S3 |', 'abnormal :', df_merge[df_merge['abnormal']==1]['S3'].mean(), '| normal :', df_merge[df_merge['abnormal']==0]['S3'].mean())
print('S4 |', 'abnormal :', df_merge[df_merge['abnormal']==1]['S4'].mean(), '| normal :', df_merge[df_merge['abnormal']==0]['S4'].mean())
결과:
S1 | abnormal : -910.6725618222323 | normal : -374.4574592183886
S2 | abnormal : -910.6725618222305 | normal : -374.457459317389
S3 | abnormal : -3662.427652993808 | normal : -1193.2474540432374
S4 | abnormal : -4473.323652485667 | normal : -1431.86631724777이들의 값들을 이상치와 이상치가 아닌 것으로 나눠서 산점도 그래프를 그려보자.
fig, ax = plt.subplots(4, 1)
sns.scatterplot(x=df_merge.index, y=df_merge['S1'], hue=df_merge['abnormal'], ax=ax[0])
sns.scatterplot(x=df_merge.index, y=df_merge['S2'], hue=df_merge['abnormal'], ax=ax[1])
sns.scatterplot(x=df_merge.index, y=df_merge['S3'], hue=df_merge['abnormal'], ax=ax[2])
sns.scatterplot(x=df_merge.index, y=df_merge['S4'], hue=df_merge['abnormal'], ax=ax[3])
plt.axhline(y=10000, color='r', linewidth=1)
plt.axhline(y=-10000, color='r', linewidth=1)
plt.gcf().set_size_inches(25, 12)
plt.show()그래프로 보았을 때, 0을 중심으로 멀리 떨어져있는 수치일 수록 이상치가 많은 것을 볼 수가 있다.
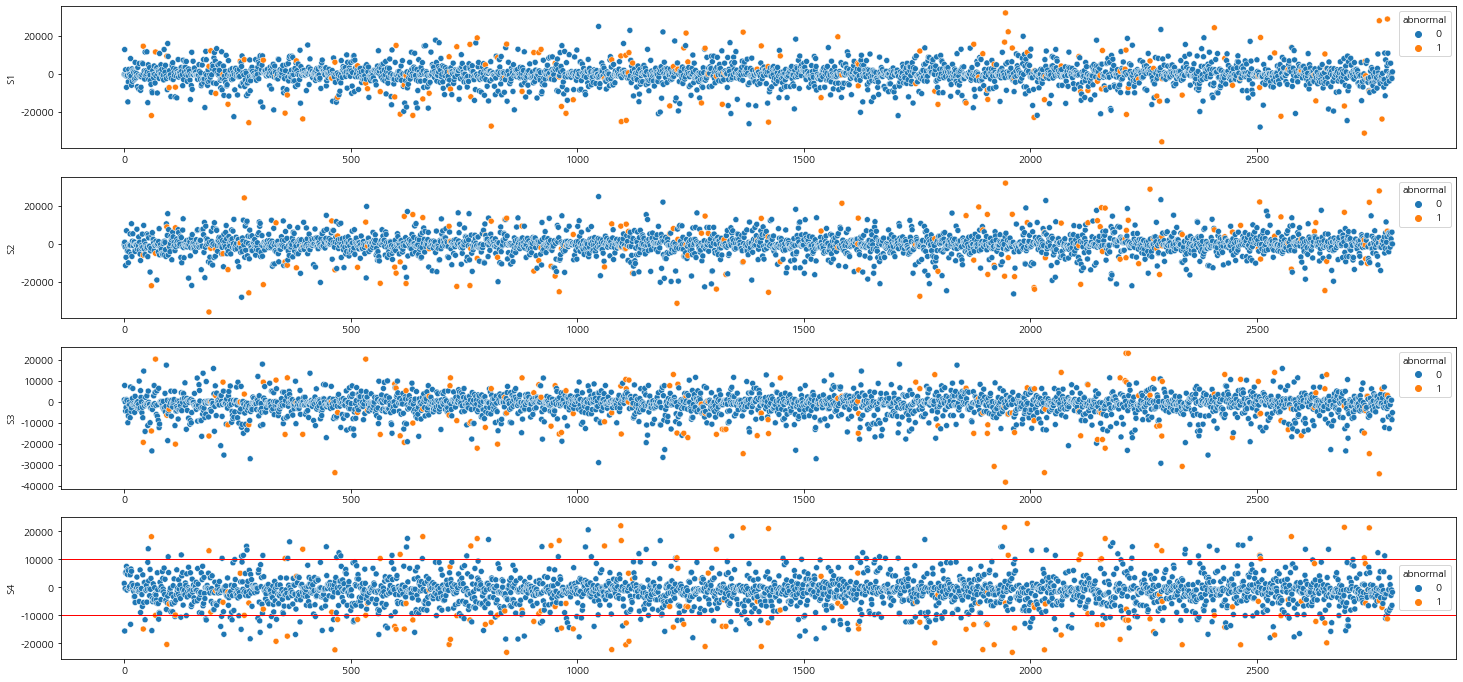
그럼 수치 10000을 기준으로 음수/양수 10000을 벗어나는 수치들 중에서 이상치의 비율을 살펴보자.
여기에서 고민이 생긴다.
과연 10000이라는 수치를 벗어나는 것들 중 이상치라 판단되는 비율이 약 30%인데,
도메인 지식이 없이 30%라는 수치를 놓고 이상치라 판단하는 근거가 될 수 있을 것인가?
classification_report
평가 지표 반환
- Precision = TP/(TP + FP) : 참이라 예측한 것들 중에서 참인 비율
- Recall = TP/(TP+FN) : 실제 참인 것 중에서 참이라고 예측한 비율
- F Score = (1 + β2)(Precision Recall) / ((β2*Precision) + Recall)
- β에 1을 넣으면 F1 score(β2 = β의 제곱)- accuracy : 모든 샘플 중에서 맞춘 것들의 비율
- macro avg : Precision, Recall, F Score별 클래스의 평균
- weighted avg : 각 클래스에 속하는 표본의 개수로 가중 평균을 내서 계산
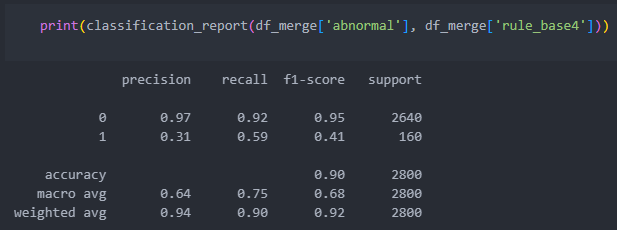
그러면 일정 수치를 벗어나는 것들을 컬럼으로 추가시킨 후에 평가 지표를 가지고 확인해보자.
이상치와 +-10000을 벗어나는 데이터들 사이의 평가 지표를 살펴보자.
S1
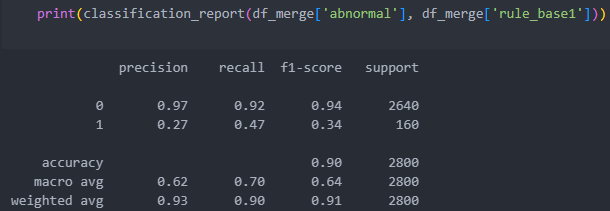
S4
모델링
분류 모델 중에서 대표적이 앙상블 계열의 RandomForestClassifier를 가지고 진행해보자.
기본 센서값으로
# 데이터 분할
X = df_merge[['S1', 'S2', 'S3', 'S4']]
Y = df_merge['abnormal']
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, stratify=Y)
train_X.shape, train_Y.shape, test_X.shape, test_Y.shape
# 인스턴스
rfc = RandomForestClassifier(random_state=29)
# 학습
rfc.fit(train_X, train_Y)
# 예측
pred = rfc.predict(test_X)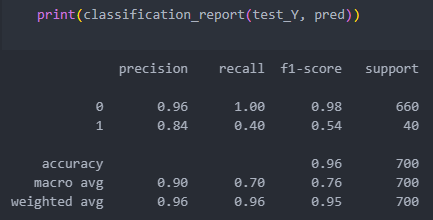
하이퍼 파라미터 튜닝
n_estimators와 max_depth의 범위를 튜닝한다.
# 하이퍼 파라미터 범위 튜닝
param_grid = {'n_estimators':[400, 500], 'max_depth':[3, 5, 10, 20]}
# 모델 인스턴스
rfc_clf = RandomForestClassifier(random_state=29, n_jobs=-1)
# 모델/하이퍼 파라미터/cv/scoring 적용
# cv : 모든 데이터를 사용하는 것이 아니라 cv등분만큼 나눠서 하나를 빼고 진행, scoring : best score를 판단할 때의 기준 score
grid_cv = GridSearchCV(rfc_clf, param_grid=param_grid, cv=3, n_jobs=-1, scoring='recall')
grid_cv.fit(train_X, train_Y)
print('best param :', grid_cv.best_params_)
print('best estimator :', grid_cv.best_estimator_)
print('best score :', grid_cv.best_score_)
결과:
best param : {'max_depth': 20, 'n_estimators': 400}
best estimator : RandomForestClassifier(max_depth=20, n_estimators=400, n_jobs=-1, random_state=29)
best score : 0.4666666666666666best score를 낸 모델 파라미터를 적용해서 보자.
# 인스턴스
rfc = RandomForestClassifier(n_estimators=400, max_depth=20, random_state=29)
#학습
rfc.fit(train_X, train_Y)
# 예측
pred = rfc.predict(test_X)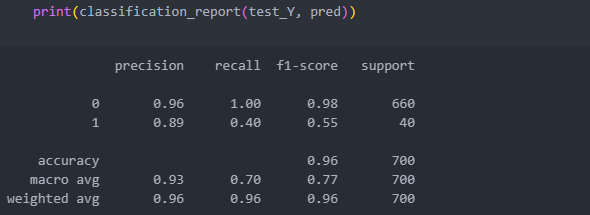
모델에 더 영향을 준 특징
featureimportances
모델을 설명할 때 영향을 많이 준 컬럼들의 설명력을 반환해준다.

그래프로 그려보자.
importance_values = rfc.feature_importances_
importance_values = pd.Series(importance_values, index=train_X.columns)
importance_values.sort_values(ascending=False, inplace=True)
sns.barplot(x=importance_values, y=importance_values.index)
plt.gcf().set_size_inches(8, 6)
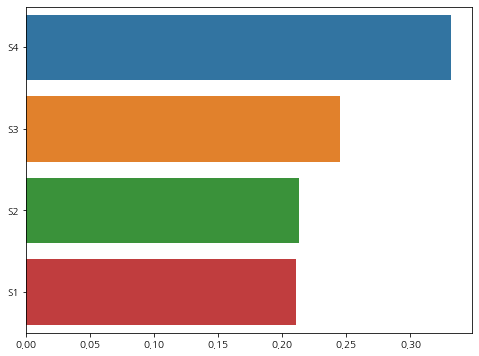
plt.show()센서들 중 이상치의 평균치가 정상 평균치보다 차이가 많이 나는 센서가 4번이었는데,
예상했듯이 이상치를 판단하는데 가장 큰 영향을 준 센서도 4번임을 알 수 있다.
변수 추가
각각의 센서들을 제곱해서 컬럼을 만들고 측정하여 다시 featureimportances를 살펴보자.
df_new = df_merge.copy()
# 변수 추가
df_new['S1_2'] = df_new['S1'] * df_new['S1']
df_new['S2_2'] = df_new['S2'] * df_new['S2']
df_new['S3_2'] = df_new['S3'] * df_new['S3']
df_new['S4_2'] = df_new['S4'] * df_new['S4']
# 필요 변수들 선택
X = df_new[['S1', 'S2', 'S3', 'S4', 'S1_2', 'S2_2', 'S3_2', 'S4_2']]
Y = df_new['abnormal']
# 데이터 분리
train_X, test_X, train_Y, test_Y = train_test_split(X, Y, stratify=Y)
# 모델 인스턴스
rfc = RandomForestClassifier(n_estimators=400, max_depth=20, random_state=29)
#학습
rfc.fit(train_X, train_Y)
# 예상
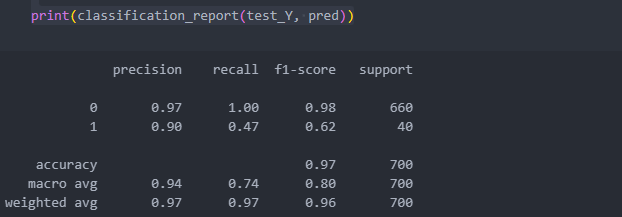
pred = rfc.predict(test_X)제곱한 변수들을 추가했는데 모델의 성능이 조금 좋아진 것을 확인할 수 있다.
featureimportances를 그래프로 그려보자.
importance_values = rfc.feature_importances_
importance_values = pd.Series(importance_values, index=train_X.columns)
importance_values.sort_values(ascending=False, inplace=True)
sns.barplot(x=importance_values, y=importance_values.index)
plt.gcf().set_size_inches(8, 6)
plt.show()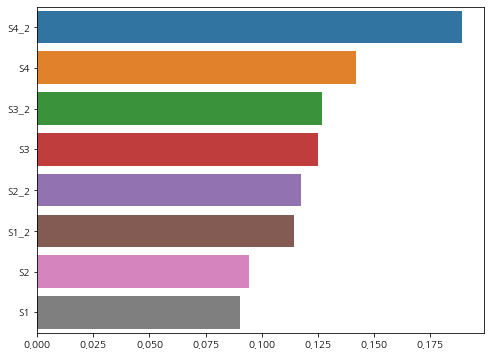
이상치를 벗어나는 것을 기준(rule base)으로 진행했을 때가 classification_report가 가장 좋다.
기대 효과
이상치를 골라내고 판단하여 무엇을 할 것인지를 문제 정의 때부터 구체적으로 고민해봐야 한다.
분석이 분석으로 끝나는 것이 아닌, 궁극적인 목표는 가치 창출임을 잊지 말아야 한다.
- 이상 징후를 사전에 탐지하여 장비 수리 및 해결책 강구 등 공정의 손실 비용 감소.
- 생산 공정 안의 손실 비용 감소만 볼 것이 아니라,
납입 기일과 납입 수량을 맞춰야 하는 회사 전체의 프로세스 안에서도 중요한 문제이고
고객과의 약속에 대한 회사의 이미지 및 신뢰도에 악영향을 미리 차단할 수 있는 방법이다.
