수업 43일차

✔ Classification - 분류 알고리즘

Logistic Regression

• odds ratio 라는 개념을 사용하는 이진 분류기
• softmax regression
  - 로지스틱 회귀는 이진 분류기인데, 원래 이진 분류기를 가지고 카테고리 분류를 하려면 ovr이나 ovo 전략을 해야 하는데, 로지싁 회귀는 이진 분류기를 훈련시켜 연결하지 않고, 직접 다중 클래스를 지원하도록 일반화 할 수 있는데, 이러한 회귀를 softmax 회귀라고 합니다.
  - 샘플 데이터가 주어지면, softmax regression model이 각 클래스에 대한 점수를 계산하고, 그 점수에 softmax function(정규화된 지수 함수)를 적용해서 각 클래스의 확률을 추정합니다.
  

• 다중 클래스 분류를 해보자. - Iris

X=iris['data'][:,(2,3)]
print(X)
y=iris['target']
print(y)

# 분류기 생성 및 훈련
softmax_reg=LogisticRegression(multi_class='multinomial', solver='lbfgs',
                              C=10, random_state=42)
softmax_reg.fit(X,y)

# 샘플 데이터 생성
# np.meshgrid : 격자 좌표를 만들어주는 함수
# x0은 아래서 생성한대로 한다면, 500행 500열 격자 생성
# np.linspace : 범위 안에 일정한 간격을 갖는 숫자 배열 생성
# np.linspace(0,1,5): [0, 0.25, 0.5, 0.75, 1.0]
x0,x1=np.meshgrid(
    np.linspace(0,8,500).reshape(-1,1),
    np.linspace(0,3.5,200).reshape(-1,1)
)
# 예측에 사용할 샘플 데이터
X_new=np.c_[x0.ravel(),x1.ravel()]

# 샘플 데이터를 가지고 예측해보기
y_predict=softmax_reg.predict(X_new)
print(y_predict)
# 샘플의 확률을 조회해보자
y_predict_proba=softmax_reg.predict_proba(X_new)
print(y_predict_proba)

SVM(Support Vector Machine)

• 매우 강력하고 선형이나 비선형 분류, 회귀, 이상치 탐지 등에 사용할 수 있는 다목적 머신 러닝 모델
• 복잡한 분류 문제에 잘 맞고, 작거나 중간 크기의 데이터 세트에 적합하다고 알려져 있습니다.
• 초평면이라는 개념을 사용해서 분류와 회귀를 수행합니다.
• 초평면은 최대 마진을 만드는 결정 경계
  - 그룹 별로 간격이 가장 크게 벌어질 수 있는 경계선을 찾는 방식
  - 이 선이 직선이면 선형, 그렇지 않다면 비선형 모델

장점

• 에러율이 낮다.
• 결과를 해석하기 용이하다.
  - 화이트박스 알고리즘

단점

• 튜닝 파라미터 및 커널 선택에 민감하다.
• 이진 분류만 가능하다
• 특성 스케일에 민감하다.

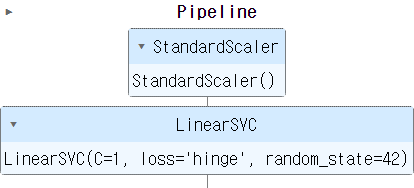
선형 SVM 모델을 이용한 이진 분류

• Pipeline
  - 여러 개의 작업을 순서대로 한꺼번에 수행하도록 해주는 개념
  - queue(순서대로)

• 선형 SVM 모델을 이용한 이진 분류

from sklearn.pipeline import Pipeline
from sklearn.svm import LinearSVC
iris=datasets.load_iris()
# feature는 2개만 사용한다.
X=iris['data'][:,(2,3)]
# 이진 분류를 수행하기 위해 2인지 아닌지 
# 타겟을 수정
y=(iris['target']==2).astype(np.float64)

# 스케일링과 훈련을 실시한 모델을 pipeline으로 구성
# 머신러닝이나 데이터 처리 등을 할 때, pipeline을 구성하는 것은 매우 중요하다.
# 만약, pipeline을 구성하지 않고 순차적으로 하나씩 해도되지만
# 코드 가독성이 떨어진다.
svm_clf=Pipeline([
    ('scaler',StandardScaler()),
    ('linear_svc',LinearSVC(C=1,loss='hinge',
                           random_state=42))
])
# 훈련 - 스케일링까지 한번에
svm_clf.fit(X,y)

# 예측 - 이진 분류이기에 1이면 2번 class true
print(svm_clf.predict([[5.5,1.7]]))

선형 SVM의 문제

• XOR 구분을 못한다.

비선형 SVM

• 결정 경계가 직선이 아니고 곡선의 형태를 가짐
• PolynomialFeatures 변환기와 StandardScaler와 LinearSVC 를 연결해서 생성

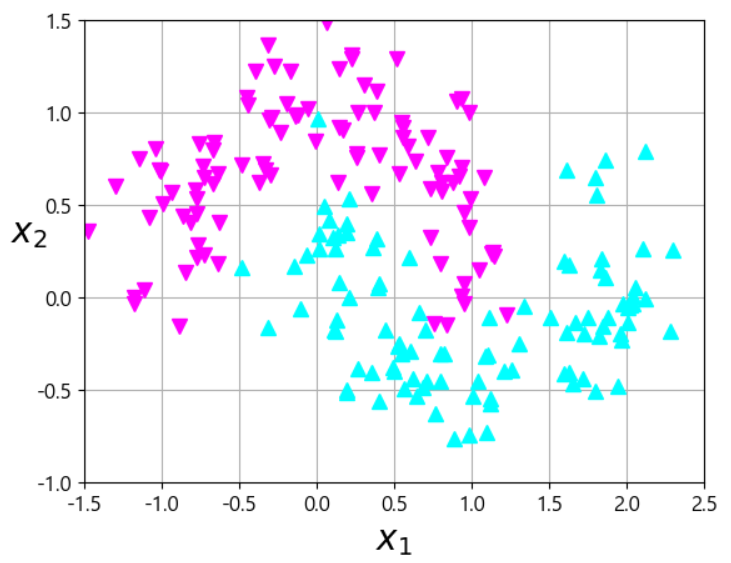
• moon dataset으로 비선형 SVM 알아가보기

# 비선형을 설명하기 위한 데이터 생성
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200,noise=0.2, random_state=42)
# 그래프로 그려봐야 압니다.
def plot_dataset(X,y,axis):
    plt.plot(X[:,0][y==0], X[:,1][y==0], 'v', color='magenta', markersize=6)
    plt.plot(X[:,0][y==1], X[:,1][y==1],'^', color='cyan', markersize=6)
    plt.axis(axis)
    plt.grid(True, which='both')
    plt.xlabel(r'$x_1$', fontsize=20)
    plt.ylabel(r'$x_2$', fontsize=20, rotation=0)
plot_dataset(X,y,[-1.5,2.5,-1,1.5])

# 비선형 SVM을 이용해서 위의 데이터를 훈련
from sklearn.preprocessing import PolynomialFeatures
# degree 값을 높이면 차수가 높아져서 곡선이 복잡해집니다.
# 훈련 데이터에 대해서는 잘 구분할 것입니다.
# 하지만 새로운 데이터가 오면 잘 구분하지 못할 수 있습니다.
# 이러한 상황을 overfitting(과적합)이라 할 수 있습니다.
polynomial_svm_clf=Pipeline([
    ('poly_feature', PolynomialFeatures(degree=3)),
    ('scaler',StandardScaler()),
    ('svm_clf',LinearSVC(C=10,loss='hinge',random_state=42))
])
polynomial_svm_clf.fit(X,y)

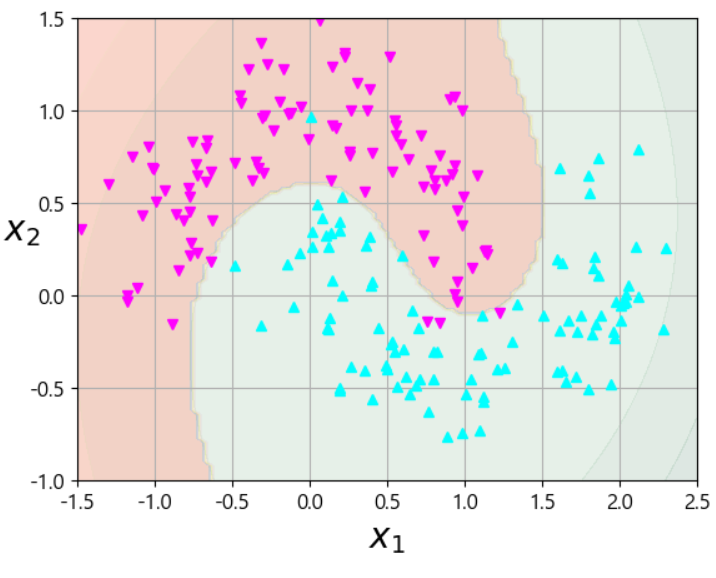
# 결정 경계와 데이터의 분포를 시각화해보자.
def plot_predictions(clf,axes):
    x0s=np.linspace(axes[0],axes[1],100)
    x1s=np.linspace(axes[2],axes[3],100)
    x0,x1=np.meshgrid(x0s,x1s)
    X=np.c_[x0.ravel(),x1.ravel()]
    y_pred=clf.predict(X).reshape(x0.shape)
    y_decision=clf.decision_function(X).reshape(x0.shape)
    plt.contourf(x0,x1,y_pred,cmap=plt.cm.brg,alpha=0.2) #cmap='Pastel1'
    plt.contourf(x0,x1,y_decision,cmap=plt.cm.brg,alpha=0.1) #cmap='YlGn'
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X,y,[-1.5, 2.5, -1, 1.5])
plt.show()
# 너무 구분을 못하는것 같으면 차수를 조금 올려보자.

다항식 커널

• degree 값을 높이게 된다면, 차수가 늘어나서 다항식이 복잡해지면서 많은 특성을 추가합니다.
• 차수가 늘어나면 데이터를 잘 분류하지만, 모델을 느리게 만듭니다.
• SVM을 사용할 때, kernel trick이라는 수학적 기교를 적용할 수 있는데, 이는 특성을 추가하지 않고 특성을 추가한 것 처럼 훈련하는 방법입니다.

유사도 특성을 추가한 커널

• 유사도 함수를 이용해서 각 특성 간의 유사도를 구한 뒤, 이 값을 특성으로 추가해서 경계를 만드는 것
• 이러한 커널을 가우시안 RBF 커널 이라고 합니다.
• 이 커널을 이용하면, 다항식을 추가한 것 과 유사한 결과를 얻을 수 있습니다.

• 가우시안 RBF 커널을 이용한 비선형 SVM

from sklearn.svm import SVC
rbf_kernel_svm_flf=Pipeline([
    ('scaler',StandardScaler()),
    # 이제 선형이 아니니 Linear 제거
    ('svm_clf',SVC(kernel='rbf', gamma=5, random_state=42))
])
rbf_kernel_svm_flf.fit(X,y)

plot_predictions(rbf_kernel_svm_flf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X,y,[-1.5, 2.5, -1, 1.5])
plt.show()

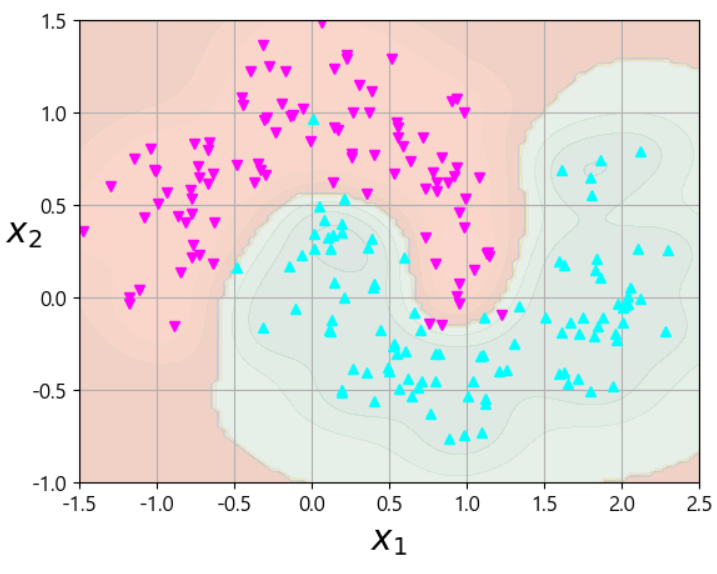
• hyper parameter로 gamma를 설정하였습니다.
• 이 값을 증가시키면 종 모양 그래프가 좁아져서 각 샘플의 영향 범위가 작아져서 결정 경계가 조금 더 불규칙해집니다.
• 작은 gamma값은 넓은 종 모양 그래프를 만들어냅니다.

• 계산 복잡도는 선형 SVM은 O(m*n)정도 이고, 커널 트릭을 사용한 경우에는 m^2 또는 ^3으로 추정됩니다. (m : 데이터의 개수)
  - 데이터의 개수가 많아지면, 훈련 시간이 급격하게 늘어납니다.
  - 10만개 정도 넘어가면 엄청 늘어납니다.

Decision Tree - 결정트리

• if의 결합
• 데이터를 분석해서 이들 사이에 존재하는 패턴을 예측 가능한 규칙들의 조합으로 만드는 모델
• 복잡한 데이터 세트에도 잘 동작하는 강력한 알고리즘
• 분류와 회귀에 모두 사용 가능합니다.
• CART라는 알고리즘을 사용해서 리프 노드 이외의 노드는 전부 자식이 2개이다.

• 모델 훈련

from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris=load_iris()
X=iris.data[:,2:]
y=iris.target
tree_clf=DecisionTreeClassifier(max_depth=2,random_state=42)
tree_clf.fit(X,y)

• 트리 모델은 GraphViz를 이용해서 시각화가 가능합니다.
• https://graphviz.org/download/#windows 에서 grahphiz 다운로드
  - path 설정 \bin, \bin\dot.exe 추가해줘야 합니다.
• conda install pygraphviz 해주기
• pip install graphviz

---

• dot file로 저장하자.

from sklearn.tree import export_graphviz
import graphviz
export_graphviz(
    tree_clf,
    out_file="iris_tree.dot",
    feature_names=iris.feature_names[2:],
    class_names=iris.target_names,
    rounded=True,
    filled=True
)

• dot file로 있던 것을 불러서 그래프 봐보자.

import os
os.environ["PATH"]+=os.pathsep+"C:/Program Files/Graphviz/bin"
with open('iris_tree.dot') as f:
    dot_graph=f.read()
src=graphviz.Source(dot_graph)
src

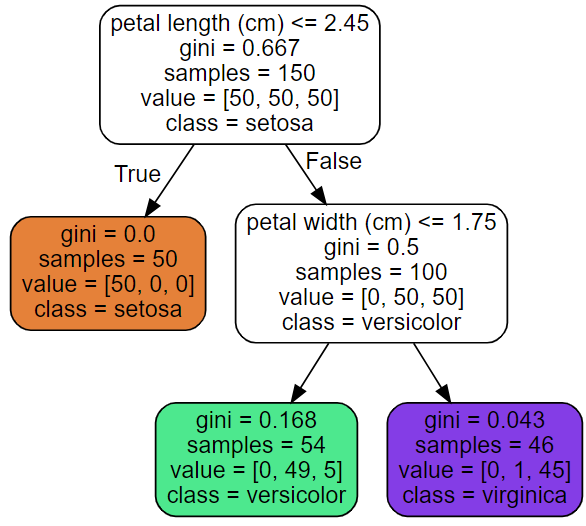
• 이것을 보고서 작성을 위해 이미지로 저장해보자.

# dot file을 이미지로 저장해보자.
import pygraphviz as pga
from IPython.display import Image
graph=pga.AGraph('./iris_tree.dot')
graph.draw('iris_tree.png', prog='dot')
Image("iris_tree.png")

• 예측 / 확률 예측

# 예측
y_pred=tree_clf.predict([[5,1.5]])
# 확률 예측
y_pred_proba=tree_clf.predict_proba([[5,1.5]])
print(y_pred)
print(y_pred_proba)

• 시간 복잡도 : O(log2(m))

불순도 지수 - gini 계수

• 이 값은 1에서 전체 데이터 중에서 각각으로 분류된 데이터의 비율을 제곱한 값을 뺀 값
• 모든 데이터가 하나의 클래스로 분류된다면 gini 계수는 0
• 샘플 개수 54개, 각각 0, 49, 5 개로 분류가 되었을 때 gini 계수는?
  - 1-(0/54)(0/54)-(49/54)(49/54)-(5/54)(5/54)=0.168
• Decision Tree 모델은 gini 계수가 낮아지도록 계속해서 학습을 해나가는 방식
• max_depth
  - 학습을 할 때, 최대로 만드는 가지의 수
  - 이 값이 크게 설정된다면 중간 가지들을 많이 만들어서 정확도가 높아지지만, 학습 시간이 늘어나게 되고, overfitting 가능성이 생깁니다.

Entropy

• Decision Tree는 기본적으로 불순도 지표로 gini 계수를 사용하는데, criterion을 entropy로 설정하면, Entropy 불순도를 사용 가능합니다.
• 무질서함을 측정하는 지표입니다.
• 0이라면 질서정연한것 (하나로 만들어진것)

Hyper Parameter

• max_depth
  - 중간 가지의 최대 깊이
• min_smaples_split
  - 분할되기 위해서 가져야 하는 노드의 최소 개수
• min_smaples_leaf
  - node(terminal)가 가져야 하는 최소 샘플의 개수
• max_leaf_nodes
  - 리프 노드의 최대 개수
• max_features
  - 각 노드에서 분할에 사용할 특성의 최대 개수
• min으로 시작하는 hyperparameter의 수를 크게 하거나 max로 시작하는 hyperparameter 수를 작게 한다면, 규제가 커집니다.
  - 규제가 커진다 == 제약조건이 많아진다 == Overfitting을 조심해야 한다.

Feature의 중요도

• 트리 모델은 feature_importances_를 이용해서 특징의 중요도를 알 수 있다.
• Feature의 중요도를 통해 중요하지 않은 피처를 제거하고 모델을 만들거나, 그런 Feature를 하나의 feature로 모아서 모델을 만들어 정확도를 높이기도 합니다.

• Titanic 생존 여부

# 데이터 가져오기
df=sns.load_dataset('titanic')

# 결측치 처리
# deck 열은 결측치가 너무 많아서 deck 열 자체를 제거하자
# embark_town은 중복되는거라 제거한거임
rdf=df.drop(['deck','embark_town'], axis=1)
# age 열은 결측치가 적기에 결측치 데이터를 제거하자
rdf=rdf.dropna(subset=['age'], how='any', axis=0)
# embarked는 결측값 2개라 최빈값으로 대체이다. (범주형이기에 최빈값으로 대체)
most_freq=rdf['embarked'].value_counts(dropna=True).idxmax()
rdf['embarked'].fillna(most_freq, inplace=True)
# 714개의 행이 전부 non-null로 존재
rdf.info()

# 어떤 것을 분석에 이용할지 고민해보자.
# 각각의 컬럼이 어떤 의미를 알고 있다? -> 도메인 지식을 어느정도 알고있다.
# 사전 지식이 없다면, 모든 열을 분석을 해봐야 한다.
rdf.head()

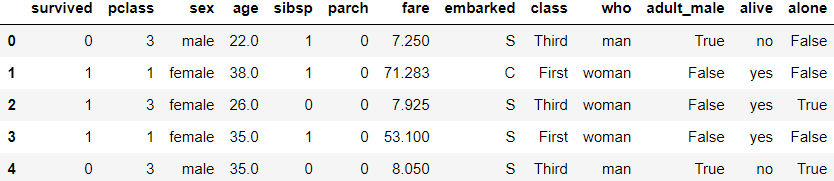
# 분석에 사용할 열 이름을 선택하자
# 이부분은 직접 결정해야 한다.
ndf=rdf[['survived','pclass','sex','age','sibsp','parch','embarked']]
ndf.info()
# 현재, sex가 object임을 확인할 수 있다.
# male, female 외 다른 것이 있는지 확인해보자.
ndf['sex'].unique()
# male, female만 존재하기에 '범주형'처리를 해주자.
# 범주형 일 떄 확인 할 것 : 순서 여부를 확인해야 한다.
# 순서가 없을 때는 one-hot-encoding
# 순서가 있는 경우에는 ordinal-encoding을 해야 한다.

• one hot encoding

# pandas의 get_dummies는 원핫 인코딩을 할 수 있다.
onehot_sex=pd.get_dummies(ndf['sex'])
# print(onehot_sex)

# embarked 열도 동일하게 처리를 해보자.
ndf['embarked'].unique()
# 순서가 없기에 원핫인코딩
# 앞에 town을 붙여서 컬럼 이름을 생성
onehot_embarked=pd.get_dummies(ndf['embarked'], prefix='town')
# 기존 df에 추가하기
ndf=pd.concat([ndf,onehot_embarked],axis=1)
ndf.head()

# 필요가 없어진 컬럼 삭제하기
ndf.drop(['sex','embarked'],axis=1,inplace=True)
ndf.head()
ndf.info()

• 데이터 더 구경하기

# feature와 target 생성
X=ndf[['pclass','age','sibsp','female','male',
'town_C','town_Q','town_S']]
y=ndf['survived']
X.head()
# X 보면 다른 값에 비에 age의 값이 너무 큼
# 정규화를 해줘야 할 것 같다.
# feature(독립변수, 설명변수)를 정규화
# feature 값들의 값의 범위나 분포 차이가 많이 나는 경우에 수행합니다.
from sklearn import preprocessing
X=preprocessing.StandardScaler().fit(X).transform(X)
print(X)

• 훈련

# 훈련데이터와 테스트 데이터 분리
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,_y_test=train_test_split(X,y,test_size=0.3,
                                               random_state=42)
print(X_train.shape)
print(X_test.shape)

# 예측을 해보자.
y_hat=tree_model.predict(X_test)
print(y_hat)

• 결과 및 feature 중요도 파악

# 예측한 결과 확인하기
print(y_hat[:10])
print(y_test.values[0:10])
# 오차 행렬 출력
from sklearn.metrics import confusion_matrix
from sklearn.metrics import classification_report
tree_matrix=confusion_matrix(y_test,y_hat)
print(tree_matrix)
# 나머지 평가 지표
tree_report=classification_report(y_test,y_hat)
print(tree_report)

# feature의 중요도 출력
n_features=X.data.shape[1]
plt.barh(np.arange(n_features),tree_model.feature_importances_, 
align='center')
plt.yticks(np.arange(n_features),['pclass','age','sibsp','female',
'male','town_C','town_Q','town_S'])
plt.xlabel('특성 중요도')
plt.ylabel('특성')
plt.ylim(-1,n_features)
plt.show()

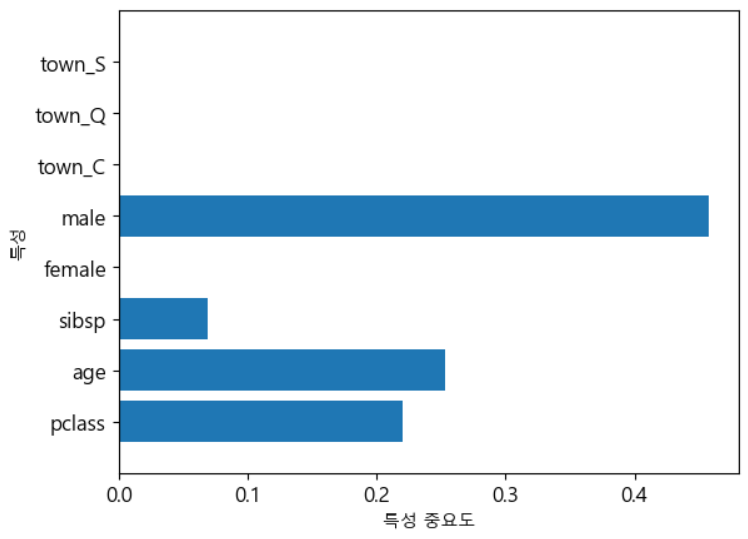
• feature의 중요도를 확인하고 중요하지 않은 feature는 제거하거나 합쳐서 하나의 feature로 만들어 모델을 마시 만드는 것도 좋은 방법 중 하나이다.
• max_depth 와 같은 하이퍼 파라미터를 수정해봐도 모델의 평가 지표는 변경될 것이다.

결정 트리의 불안정성

• 이해하기 쉽고 사용하기 편하고 성능도 우수하다
• 결정트리는 계단 모영의 결정 경계를 만들기 때문에, 훈련 세트의 회전에 취약
• 결정 트리를 만들어서 훈련하기 전에 PCA를 이용해서 데이터를 더 좋은 방향으로 회전시키는 것이 성능에 도움이 된다.

• 최적의 파라미터를 찾아보자.

# 최적의 parameter를 찾아보자.
from sklearn.model_selection import GridSearchCV
params={
    'max_depth':[3,5,10,15,20,40],
    'min_samples_split':[4,8,16,24,32,64]
}
grid_cv=GridSearchCV(tree_model,param_grid=params,
scoring='accuracy',cv=5,verbose=1)
grid_cv.fit(X_train,y_train)
print("최고 정확도 : ", grid_cv.best_score_)
print("최고 파라미터 : ",grid_cv.best_params_)

• scoring: 모델 성능 평가 지표를 설정합니다. 여기서는 'accuracy'로 설정하여 정확도를 평가합니다.
• cv: 교차 검증을 수행할 폴드 수 또는 교차 검증 분할기를 지정합니다.
• verbose: 그리드 서치의 진행 과정을 얼마나 자세히 출력할지를 설정합니다. 값이 클수록 더 자세한 출력이 됩니다.

✔ Regression - 회귀

개요

• 한 개의 종속 변수(target)와 독립 변수(feature)들 간의 관계를 모델링 하는 것으로, 종속 변수가 연속형이다.

종류

• 단순 회귀
  - 독립 변수가 1개인 경우
• 다중 회귀
  - 독립 변수가 2개 이상인 경우
• 선형 회귀
  - 일차 방정식 형태로 직선의 모양
• 비선형 회귀
  - 다항 방정식 형태로 곡선의 모양
  

선형 회귀

• 실제 값과 예측 값의 차이(잔차)의 제곱 값이 최소화되는 직선형 회귀선을 최적화하는 방식

종류 - 규제 방법(회귀 계수에 패널티 부여)에 따라 분류

• Ridge
  - 선형 회귀에 L2 규제를 가한 회귀 모델
  - 상대적으로 큰 회귀 계수의 값의 예측 영향도를 감소시키기 위해서 회귀 계수의 값을 더 작게 만드는 모델
• Lasso
  - 선형 회귀에 L1 규제를 가한 회귀 모델
  - 예측 영향력이 적은 feature의 회귀 계수를 0으로 만드는 방식
  - feature selection이라고도 합니다.
• ElasticNet
  - L2와 L1 규제를 함께 결합한 모델로, feature가 많은 data set에 적용합니다.

평가 지표

• MAE(Mean Absolute Error)
  - 실제 값과 예측 값의 차이를 절대값으로 변환하고 더한 평균
• MSE(Mean Square Error)
  - 실제 값과 예측 값의 차이에 제곱한 값의 평균
  - 많이 사용
  - 제곱을 하기에 값이 매우 커질 수 있다.
• RMSE(Root Mean Square Error)
  - MSE의 제곱근
  - MSE는 제곱 값이기에 기존 데이터보다 크게 나오는 경향이 있습니다.
• MSLE와 RMSLE
  - Log를 취한 값
• 결정 계수 (R2)
  - 1-{(실제 값-target의 평균값)^2의 합 / (실제값-예측값)^2의 합}
  - 실제값==예측값 이라면 1.0에 가까워 질 것이다.
• sklearn의 scoring
  - 결정 계수를 제외한 모든 평가 지표는 적을 수록 좋은 지표
  - sklearn에서는 평가 점수를 판단할 때는 높은 것을 좋은 것으로 판단하기 위해서 neg_mean_squared_error를 사용해서 음의 MSE를 사용함
  

선형 회귀 알고리즘

• 정규 방정식(sklearn 지원X, 직접 만들기)
  - 행의 개수는 많아지더라도 속도에 영향을 주지 않음
  - feature의 개수가 많아지면 속도가 느려짐
  - 스케일 조정이 필요없음(정규화 필요 x)
  - 비용을 최소화하는 세타 값을 찾기 위한 해석적인 방법
  - 역행렬을 계산하고 행렬 곱셈을 수행해서 계산

# 샘플 데이터 생성
X=2*np.random.rand(100,1) # 100개의 독립변수
y=4+3*X+np.random.randn(100,1) # 100개의 노이즈가 섞인 종속 변수 생성
# 여기서 기울기와 절편을 어떻게 구할 것인가?
# 모든 샘플에 1을 추가
X_b=np.c_[np.ones((100,1)),X]
# 역행렬을 구하고(inv) 행렬 곱셈(dot)을 수행
theta_best=np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
print(theta_best) # noise로 인해 정확히 4와 3이 안나옴

# 예측
X_new=np.array([[0],[2]])
X_new_b=np.c_[np.ones((2,1)),X_new]
y_predict=X_new_b.dot(theta_best)
print(y_predict)

---

• 경사 하강법(Gradient Descent)
  - 비용 함수를 최소화하기 위해서 반복해서 파라미터를 조정해나가는 방식
  - 일단 무작위로 Y=w*X+b 식을 생성하고, 여기서 MSE를 최소로 하는 w와 b를 찾아나가는 방식
  - 학습률 : 스텝의 크기로, 하이퍼 파라미터로 조정합니다.
  - 학습률이 너무 작다면 알고리즘이 수렴하기 위해 많은 반복 필요함(많은 시간)
  - 학습률이 너무 크다면, 알고리즘이 수렴하지 못하는 경우가 발생할 수 있음
  - 스케일링을 해야만 잘 동작한다

---

• SVD(특이값 분해)
  - sklearn LinearRegression Class
  - 행의 개수는 많아지더라도 속도에 영향을 주지 않음
  - feature의 개수가 많아지면 속도가 느려짐
  - 스케일 조정이 필요 없음(정규화 필요 X)

---

• 배치 경사 하강법(Data 많다면 가장 느리다)
  - Batch : 일괄, 모아서 $\rarr$ 실시간 처리하기엔 너무 많은 데이터
  - sklearn SGDRegressor Class
  - 행의 개수가 많아진다면 학습 속도가 느려집니다.
  - feature 개수 많아지더라도 속도에는 거의 영향이 없음
  - 스케일 조정이 필요함
  - 매 스텝마다 전체 데이터를 가지고 학습하는 방식
  - 모든 경우를 바라보고 학습을 합니다. $\rarr$ 속도가 느림

---

• 확률적 경사 하강법
  - sklearn SGDRegressor Class
  - 행의 개수는 많아지더라도 속도에 영향을 주지 않음
  - feature 개수 많아지더라도 속도에는 거의 영향이 없음
  - 스케일 조정이 필요함
  - 무작위 샘플을 이용해서 경사를 계산하므로, 배치 경사 하강법보다는 빠르지만, 불안정합니다.

---

• 미니 배치 경사 하강법
  - sklearn SGDRegressor Class
  - 행의 개수는 많아지더라도 속도에 영향을 주지 않음
  - feature 개수 많아지더라도 속도에는 거의 영향이 없음
  - 스케일 조정이 필요함
  - 작은 샘플 set을 이용하는 방식
  - GPU를 사용하는 경우에 성능이 매우 향상됩니다.

---

skelarn.linear_model.LinearRegression

• 잔차의 합이 최소가 되도록 회귀식을 계산해주는 클래스
• LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
  - fit_intercept : 절편을 계산할지 여부, False : 절편(intercept) 0
  - normalize : fit_intercept가 True일 때만 사용 가능, 정규화 작업
  - copy_X : 복제를 해서 수행할 것인가? 기본값 True
  - n_jobs : 훈련에 사용할 코어의 개수로 -1이면 모든 코어 사용
• fit 함수의 결과로 coef(회귀 계수)와 intercept_(절편)가 생성됩니다.

회귀 계수는 Input Feature의 독립성에 영향을 많이 받습니다.

• input feature간에 상관관계가 매우 높은 경우, 오류에 매우 민감해지는데, 이러한 현상을 다중공선성(multil-conlinearity)문제라고 합니다.
• 회귀를 수행할 때는 독립 변수들 간의 상관 관계를 확인해야 합니다.

단순 선형 회귀의 경우는 scipy package의 stats 모듈의 linregress 함수를 이용해서 추정 가능합니다.

• 기울기, 절편, 상관 계수, p-value, 에러의 표준 편차가 순차적으로 반환 됩니다.

보스톤 주택 정보를 이용한 선형 회귀

• 506개의 데이터와 14개의 컬럼으로 구성되어 있습니다.
• CRIM : 범죄율
• ZN : 큰 주택 비율
• INDUS : 상업 지역 비율
• CHAS : 찰스 강 인접 여부(CATEGORY)
• NOX : 일산화질소 여부
• RM : 주택의 방 개수
• AGE : 1940년 이전에 지어진 자가 주택 비율
• DIS : 직업 센터까지의 접근성 지수
• RAD : 큰 도로까지의 접근성 지수
• TAX : 재산 세율
• PTRATIO : 학생/교사 비율
• B : 흑인 비율
• LSTAT : 하위 계층 비율
• MEDV(PRICE-TARGET): 주택 가격

---

# 데이터 가져오기
data_url='http://lib.stat.cmu.edu/datasets/boston'
raw_df=pd.read_csv(data_url, sep='\s+', skiprows=22, header=None)
data=np.hstack([raw_df.values[::2,:],raw_df.values[1::2,:2]])
target=raw_df.values[1::2,2]

# boston 데이터 세트 DataFrame 변환
bostonDF = pd.DataFrame(data, columns = ["CRIM","ZN","INDUS","CHAS", 
"NOX", "RM", "AGE", "DIS", "RAD", "TAX", "PTRATIO", "B", "LSTAT"])
# boston 데이터 세트의 target 배열은 주택 가격임 . 
# 이를 PRICE 칼럼으로 DataFrame에 추가
bostonDF['PRICE'] = target
print('Boston 데이터 세트 크기 :', bostonDF.shape)
bostonDF.head()

# 상관 관계를 파악하고자 하는 열의 리스트
cols=['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD','PRICE']
# bostonDF[cols].corr()
sns.pairplot(bostonDF[cols],height=2.5)
plt.show()

• feature로 사용할 열의 상관관계를 파악할 필요가 있습니다.
• 상관관계가 높다면, 다중공선성 발생 가능성이 있기 때문입니다.

# y의 자리만 다른 컬럼 이름으로 수정하면 
# 그 컬럼과의 상관관계를 파악하는 것이 가능합니다.
fig, axs=plt.subplots(figsize=(16,8), ncols=4, nrows=2)
lm_features=['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD']
for i, feature in enumerate(lm_features):
    row=int(i/4)
    col=i%4
    sns.regplot(x=feature,y='PRICE', data=bostonDF,ax=axs[row][col])
    # price를 다른걸로 바꿔서 해봐도 됩니다.
    # 우선 rm, lstat이 좀 상관관계가 높은 것 같다.

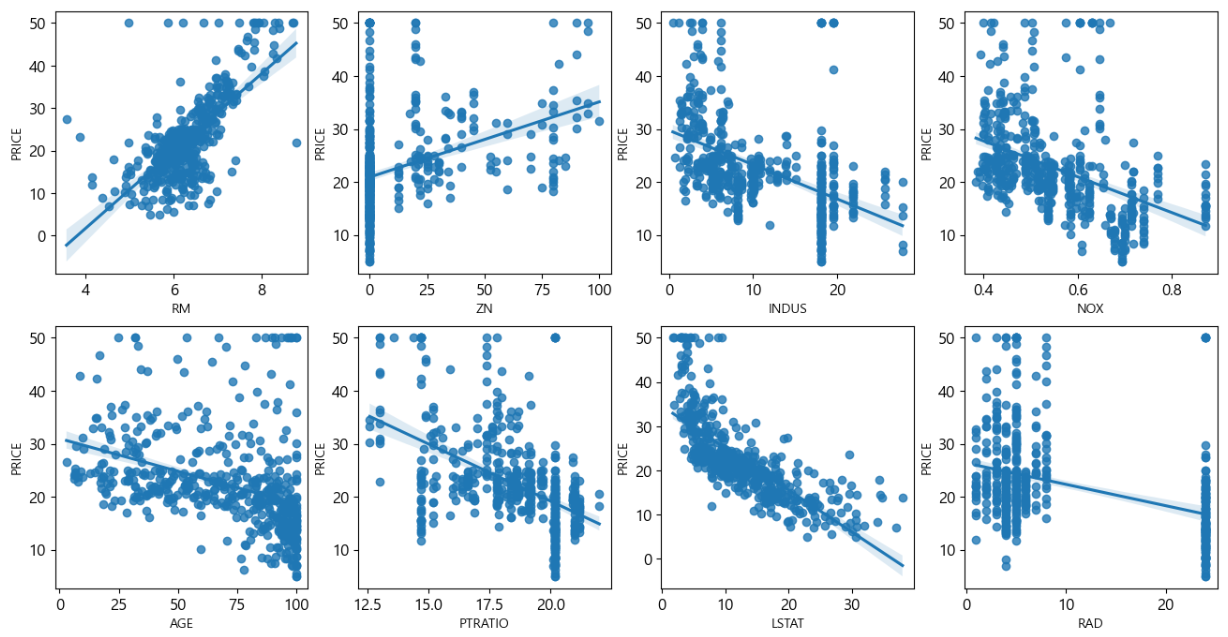
RM(방의 개수)를 이용한 Price(주택 가격) 예측 : 단변량 선형 회귀

from scipy import stats
slope, intercept, r_value, p_value,
stderr=stats.linregress(bostonDF['RM'], bostonDF['PRICE'])
print('기울기 : ', slope)
print('절편 : ', intercept)
print('상관 계수 : ', r_value)
print('불확실성 정도 : ', p_value)
print('방이 4개인 주택의 가격 : ', 4*slope+intercept)

# 이번엔 sklearn
from sklearn.linear_model import LinearRegression
slr=LinearRegression()
X=bostonDF[['RM']].values
y=bostonDF['PRICE'].values
slr.fit(X,y)
# 기울기가 값이 아닌 배열 형태로 나왔다.
print('기울기 : ', slr.coef_)
print('절편 : ', slr.intercept_)

선형 회귀에서의 Outlier

• 선형 회귀 모델은 이상치에 영향을 많이 받음
• 해결책
  - 이상치를 감지해서 제거하고 수행
  - 이상치를 제거하지 않고, RANSAC(RANdom Sampel Consensus)방식으로 해결하기
• RANSAC
  - 랜덤하게 일부 샘플을 선택해서 모델을 훈련
  - 훈련된 모델을 가지고 다른 모든 데이터를 테스트하고, 분석가가 입력한 허용 오차 안에 속한 데이터를 정상적인 데이터로 추가
  - 정상적인 데이터만을 가지고 다시 훈련
  - 훈련된 모델과 정상적인 데이터와의 오차를 추정
  - 성능이 사용자가 지정한 임계값에 도달하거나, 지정된 반복 횟수에 도달하면 알고리즘 종료

RANSACRegressor 클래스를 이용한 회귀

• 매개변수
  - max_trials : 최대 반복 횟수
  - min_samples : 최소 샘플 개수
  - loss : 오차 측정 함수
  - residual_threshold : 오차의 임계값

# RANSAC을 이용한 회귀
from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(), 
                            max_trials=100, 
                            min_samples=50, 
                            loss='absolute_error', 
                            residual_threshold=5.0, 
                            random_state=42)
ransac.fit(X,y)
# 이상치를 제거하고 만들었더니 이전과는 결과가 보인다.
print('기울기 : ', ransac.estimator_.coef_[0])
print('절편 : ', ransac.estimator_.intercept_)

회귀의 성능 평가

• MSE와 같은 오차 값을 이용하거나 R2같은 값을 이용합니다
• 오차 값음 높은 것이 성능이 안좋은 것이고, R2는 1에 가까운 값이 성능이 좋은 값
• MSE를 볼 때는 target값과 비교
• 거의 모든 모델은 훈련 데이터에 비해서 테스트 데이터에서 성능이 나쁜데, 이 차이를 가지고 일반화 성능을 평가한다.
• 이 차이가 크다면 overfitting이다.

from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
print("훈련 데이터의 평균 제곱 오차 : ",
mean_squared_error(y_train, y_train_pred))
print("테스트 데이터의 평균 제곱 오차 : ",
mean_squared_error(y_test, y_test_pred))
print("훈련 데이터의 R2 SCORE : ", r2_score(y_train, y_train_pred))
print("테스트 데이터의 R2 SCORE : ", r2_score(y_test, y_test_pred))

• r2 score는 높은 것이 좋고, mse는 낮은게 좋다.
• r2 score를 보면 underfitting 임을 알 수 있다

성능 평가 결과 해석

• 훈련 데이터와 테스트 데이터의 성능 평가 지표의 값이 비슷하면, 일반화가 잘 된 경우이다.
• 훈련 데이터를 가지고 수행한 결과가 월등하게 좋다면 Overfitting
• 훈련 데이터를 가지고 수행한 결과가 더 나쁘다면 Underfitting
  - 이 경우에는 훈련 데이터 개수를 늘리거나, 다른 속성을 추가해서 회귀 분석을 다시 수행해야 한다.
  

다변량 회귀 분석

• 독립 변수의 개수가 2개 이상인 경우
• LinearRegression 클래스를 이용해서 수행 가능합니다.
• 독립변수만 바꾸면 알아서 다변량 회귀 분석을 실시함
• 다변량 회귀를 할 때, 주의할 점은 다중 공선성문제이다.