- 전체보기(56)
- C(51)
- leetcode(45)
- recursion(12)
- Two pointers(6)
- DP(6)
- array(4)
- binary_search(4)
- linkedlist(4)
- Failed(4)
- 수학(3)
- boj(3)
- 테일러 급수(3)
- greedy(2)
- C++(2)
- bitwise(2)
- 급수(2)
- dynamic programming(2)
- 에라토스테네스의 체(2)
- sinx/x(2)
- String(2)
- 시뮬레이션(2)
- brute force(2)
- stack(2)
- sorting(1)
- loop(1)
- combination(1)
- 바젤 문제(1)
- 테일러 정리(1)
- Median(1)
- 소수(1)
- xor(1)
- shift(1)
- 매클로린 급수(1)
- Boyer-Moore Voting Algorithm(1)
- 극한(1)
- 거듭제곱(1)
- 오일러(1)
- Binary Search(1)
- 미적분학(1)
- 과반수(1)
- 해석학(1)
- base26(1)
- 수열(1)
- squeeze theorem(1)
- Alogorithm(1)
- 수열의 합(1)
- linked list(1)
- 오일러 곱(1)
- memoization(1)
- 시간복잡도(1)
- 조화 급수(1)
- 투포인터(1)
- 배수(1)
- matrix(1)
- 정수론(1)
- 배타적논리합(1)
- 파스칼 삼각형(1)
- Prefix sum(1)
- palindrome(1)
- POWER(1)
[BOJ] 21609. 상어 중학교
Intuition 문제의 조건만 잘 생각하면서 푼다면 큰 어려움은 없다. 다만 구현량이 지금까지 경험했던 문제들에 비해서 조금 많다. Approach 및 개선점 BFS vs DFS 블록 그룹들을 찾는 탐색 방식으로 BFS와 DFS를 떠올려 볼 수 있다. 둘 중 어느 방식을 쓰든 이 문제에서는 큰 차이가 없다. 나는 DFS를 썼다. 다만, 삼성 코딩테스트에...
[BOJ] 14503. 로봇청소기
Intuition 문제에 기술되어 있는 대로 구현만 하면 된다. 특별한 알고리즘이 필요하지 않았다. Approach 좌표 처리 네 방향의 좌표들을 편리하게 처리하기 위해 아래 같은 방식을 사용했다. 테두리 이런 배열을 활용하는 문제는 항상 테두리에 주의해야 한다. 배
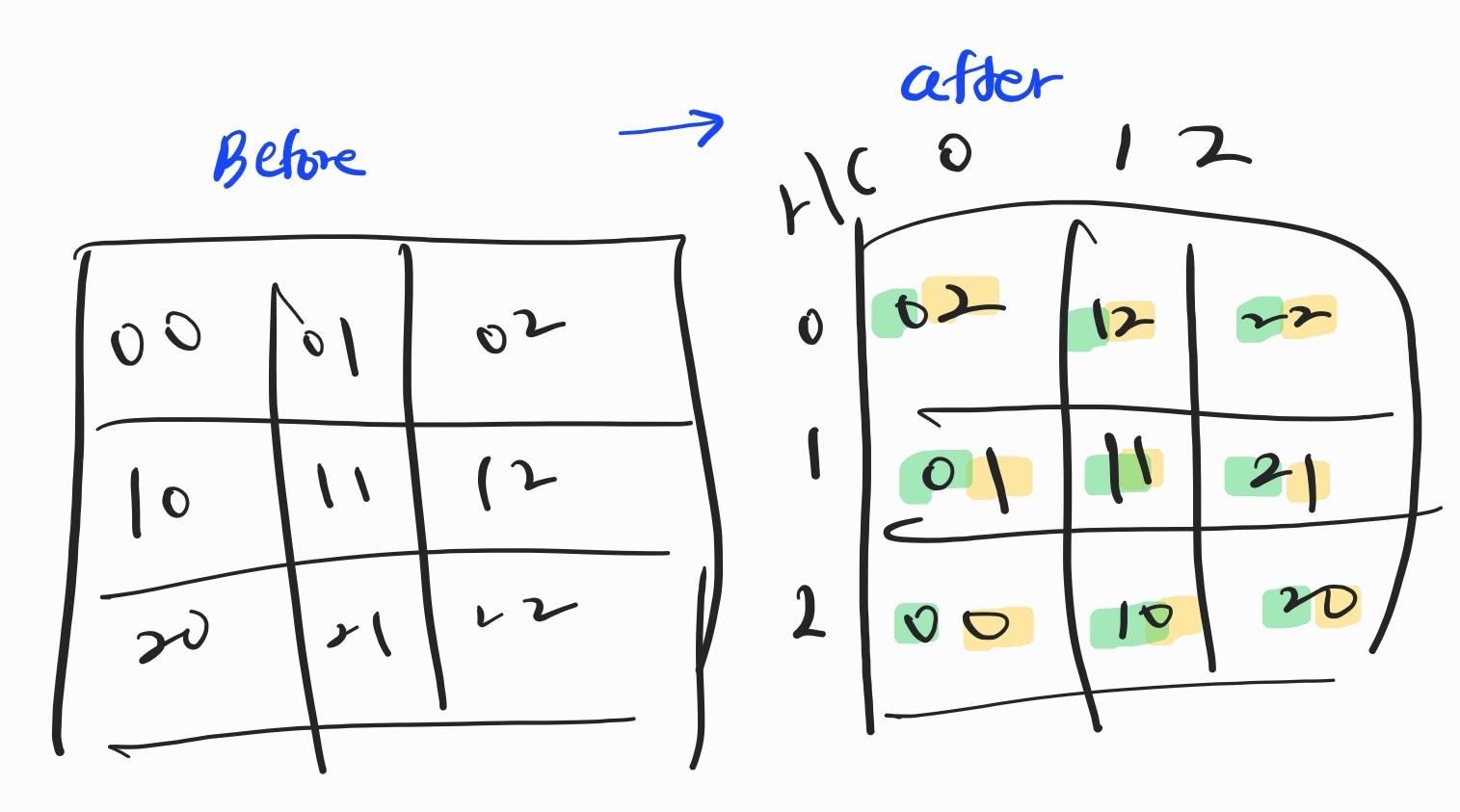
[LeetCode] 312. Burst Balloons
Intuition 하나씩 풍선을 터뜨려가면서 그때그때 최선의 선택을 찾는 알고리즘은 불가능해보였다. 작은 케이스의 결과가 큰 케이스의 결과를 알아내는 데에 도움을 줄 수 있어보였다. Approach >Def.) numsi:j]에서 최대로 구할 수 있는 코인의 수를 co

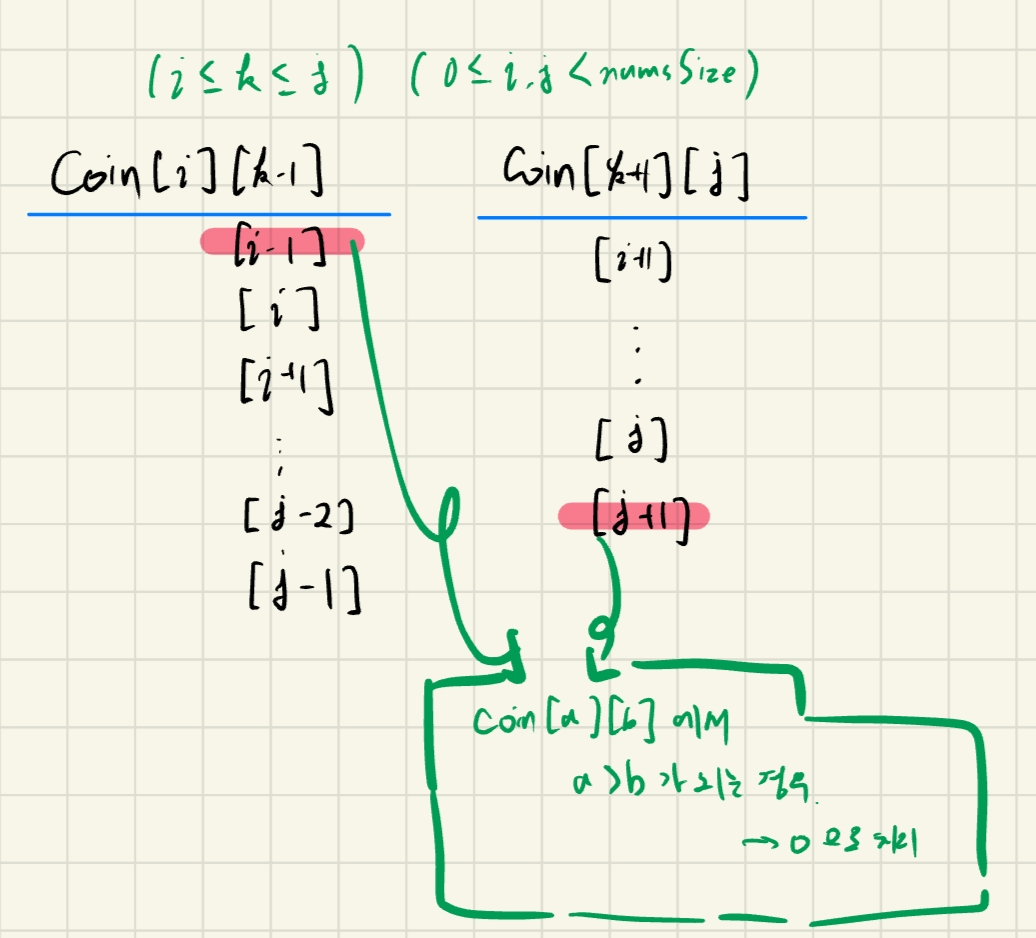
[LeetCode] 72. Edit Distance
Intuition 작은 문자열부터 원래문자열까지 하나씩 늘려가며 문제를 해결할 수 있을 것이라 예측했다. Approach 문제 재해석 >Def.) arri:=word1[:i]가 $word2[:j]로 convert 되는데 필요한 최소 cost 위와 같이 부분 문제를 정
[LeetCode] 1143. Longest Common Subsequence
Intuiton longest와 subsequence의 키워드로 DP풀이를 고려해볼 수 있다. text1과 text2의 문자를 하나씩 비교하며 같을 때마다 Longest Common Subsequence(이하 LCS)의 길이가 +1될 것이라고 예상했다. Approach
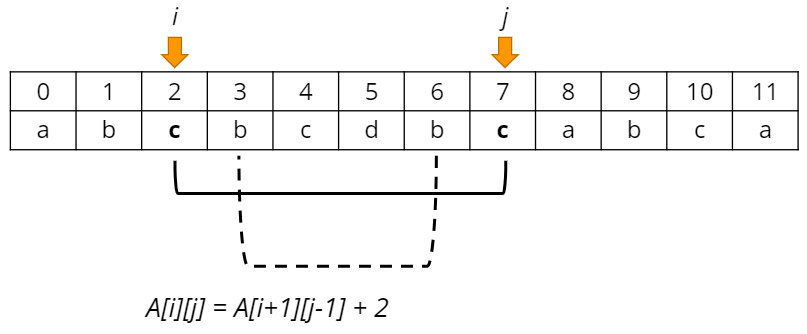
[LeetCode] 516. Longest Palindromic Subsequence
Intuition 임의의 두 문자가 같거나 다른지에 따라 관계식에 변화가 있을 것이라고 추정했다. Approach >Ai : [i:j]의 범위에서 Longest Palindromic Subsequence(이하 LPS) 위와 같이 문제를 정의한다. 길이가 1인경우에는

[LeetCode] 416. Partition Equal Subset Sum
Intuition 각 원소들의 사용여부에 대해 모든 경우의 수를 따져본다. Approach [1,5,11,5] 의 배열을 예시로 들겠다. 전체합의 반인 11을 만들 수 있는지 확인해야한다. 첫번째 원소 1의 경우 사용하지 않게 되면 0을 만들 수 있고, 사용하면 1을
[LeetCode] 279. Perfect Squares
제곱수들만의 합으로 특정 숫자를 구성한다. 이때, 최소한의 숫자가 몇개인지 구하는 문제이다.LIS의 변형 느낌이다.이번 문제는 쉽기때문에 간단하게 요약 작성하였다1을 만들기 위해서는 1만 있으면 된다.2는 1+1, 0+2 모두 가능하지만, 문제 조건상 전자만 가능하다.
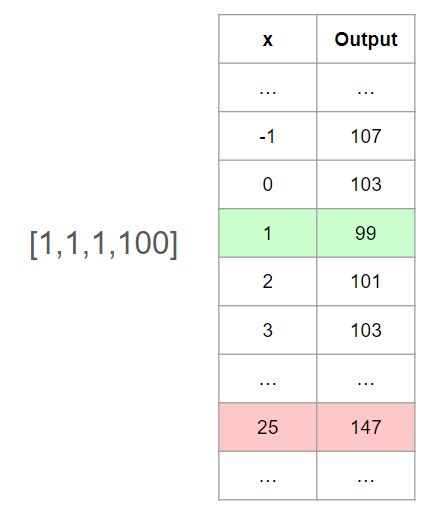
[LeetCode] 462. Minimum Moves to Equal Array Elements II
Intuition $argminx\sum\left\vert arri-x \right\vert$을 찾는 문제로 귀결된다. 이때 $x$는 중간의 적당한 어떤 값인 평균이나 중앙값 중 하나일 것이라고 추측했다. Approach 중앙값일 때 결과값이 최소화되고 중앙값에서 멀어

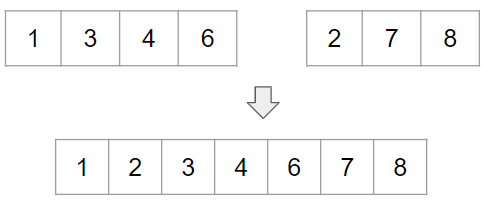
[LeetCode] 946. Validate Stack Sequences
pushed의 원소들을 stack에 push하면서 popped의 원소들과 비교해본다.예시를 들어보겠다. sp는 stack pointer, pushp와 popp는 각각 push pointer, pop pointer다.1,2,3은 popp의 4와 일치하지 않으므로 모두 s
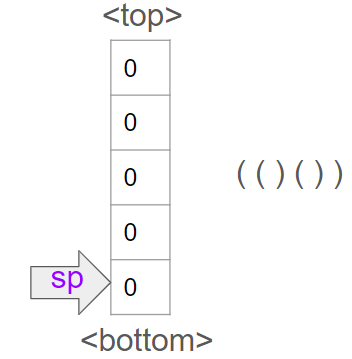
[LeetCode] 856. Score of Parentheses
Intuition stack 에 여는괄호 '(' 를 넣으면서 닫는괄호 ')' 가 나올 때마다 경우에 맞게 처리해주는 방식으로 풀이했다. Approach '(()())' 을 예시로 설명해보겠다. 그림으로 표현해보면 아래와 같은 상황이다. sp는 스택포인터다. 여는 괄호
[LeetCode] 4. Median of Two Sorted Arrays
Intuition $O(log(m+n))$의 시간 복잡도 내에 문제를 해결해야 하기 때문에, 실제로 두 배열을 합치는 방식은 배제한다. 실제로 정렬을 수행하지 않으면서 median을 찾는 방법을 고안해야한다. 중앙값이 $N$개의 원소들을 정렬했을 때 $N\over2$

[LeetCode] 33. Search in Rotated Sorted Array
Intuition 문제에서 한번 회전된 배열이 input으로 들어오는 경우, 이진탐색을 적용할 수 없다. 즉, 회전되기 전의 배열을 구해야한다. Approach 회전되기 이전의 배열을 구하기 위해 회전이 된 기준점인 pivot을 이진탐색을 통해 탐색했다. >우선, numsSize가 1인 경우의 pivot은 0일수밖에 없고, 회전이 되어있지 않은 케이스는 ...
[LeetCode] 275. H-Index II
Intuition citations.length에 따라 h의 최댓값이 결정되는 점에 주목하여 이진탐색을 진행했다. Approach [3,3,100] 이라는 배열이 있을 때, 배열의 길이가 3이므로 h는 최소1, 최소3 의 범위 내에서 구할 수 있다. 1부터 3까지의
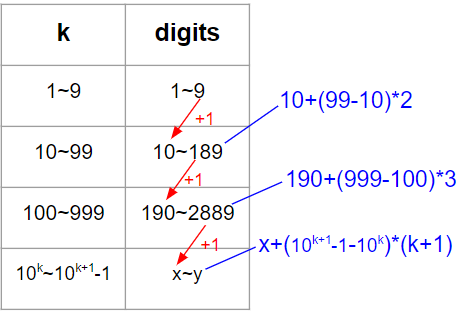
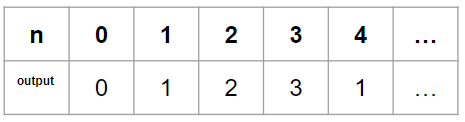
[LeetCode] 400. Nth Digit
Intuition 이진탐색으로 output후보를 탐색하면서, 그때그때마다 해당 후보가 정답범위에 있는지를 체크하기로 했다. Approach 예를 들어 12는 10에서 2만큼 차이가 나고, 또 두자리수이기 때문에 10에서 1씩 커질때마다 digits는 2씩 증가한다. 따

[LeetCode] 1011. Capacity To Ship Packages Within D Days
Intuition 가능한 capacity를 이진탐색을 통해 후보를 정한 다음, 그때그때 그것이 가능한지 체크한다. 이때, 점점 capacity가 작아지도록 이진탐색하여 최솟값을 찾는다. Approach >어떤 시점 x부터는 capacity가 모두 가능해진다. 이 x를 찾기 위해 이진탐색을 진행할 것이다. 위의 표에서는 편의를 위해 최댓값을 $2^{31}$...
[LeetCode] 1079. Letter Tile Possibilities
Intuition 같은 문자끼리는 구분하지 않으므로 개수를 기준으로 풀이하면 될 것이라 생각했다. Approach&Solution 교수님 풀이 예를 들어, 우리가 모든 문자를 다 써야하는 문제라면 단순히 팩토리얼 계산으로도 쉽게 해결할 수 있다. (특히, 이 문제의
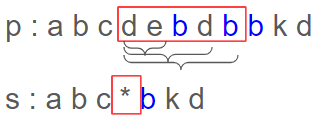
[LeetCode] 44. Wildcard Matching
Intuition '*'가 등장할 때마다 이를 분기로 삼고 재귀를 호출하는 방식으로 진행하면 되겠다고 생각했다. 그리고 이렇게 가능성 있는 케이스를 모두 살펴보고 한번이라도 가능한 케이스가 발견되면 true를 반환하면 될 것이라고 생각했다. Approach >문자열 s와p 둘 중 하나라도 끝날때까지 문자열을 순회한다. 이때, 두 문자가 같지 않은 경우는 따...
[LeetCode] 52. N-Queens II
Intuition 퀸이 공격할 수 있는 가로,세로, 대각선 방향을 체크하면 되겠다고 생각했다. Approach 퀸을 배치할 때마다, 이전에 놓인 퀸 중 가로, 세로, 대각선 방향으로 공격할 수 있는 퀸이 존재하는지 확인해야 한다. >이를 위해 이 체스판 좌표의 특징(
[LeetCode] 733. Flood Fill
Intuition 4-directionally라는 문제 조건에 맞춰, 재귀함수를 상하좌우로 호출하면 될 것이라고 생각했다. Approach >본격적으로 문제를 풀기에 앞서 2차원 배열을 반환하기 위한 세팅을 해줘야한다. 관련 설명은 [LeetCode] 77. Combinations에 기술했다. >특정 좌표에 문제에서 원하는 color로 색칠을 해주는 함수...
