Intuition

퀸이 공격할 수 있는 가로,세로, 대각선 방향을 체크하면 되겠다고 생각했다.

Approach

퀸을 배치할 때마다, 이전에 놓인 퀸 중 가로, 세로, 대각선 방향으로 공격할 수 있는 퀸이 존재하는지 확인해야 한다.

그러나, 직접 퀸의 좌표를 저장하는 것 대신 체스판 좌표의 특징(?) 을 활용해 볼 수 있다.
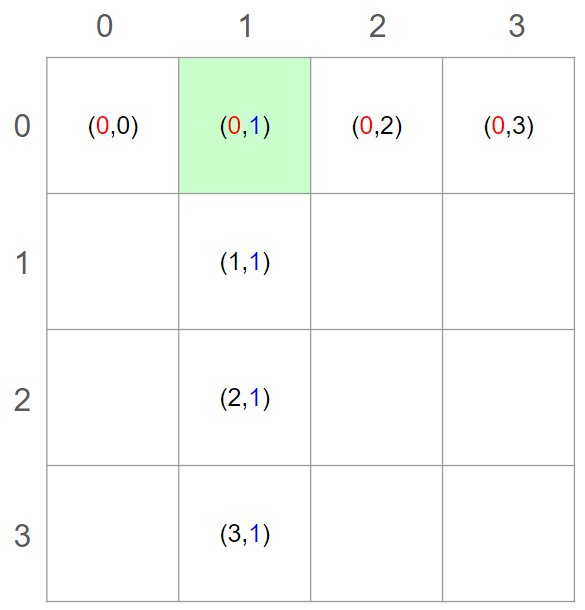
가령, (0,1)에 퀸이 있을 경우 다음에 오는 퀸의
row값은 0이 될 수 없고,
column값은 1이 될 수 없다.

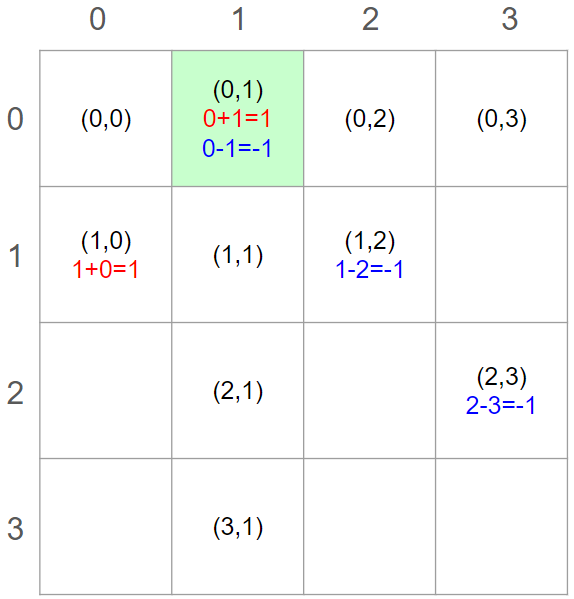
대각선 방향은 합 또는 차가 같은 경우로 구분할 수 있다.

따라서, 각각의 경우를 masking하는 배열을 만들어서 $O(1)$만에 특정좌표가 배치가 가능한지 알 수 있다.
row의 경우는 재귀함수의 인자를 통해 구분하고,
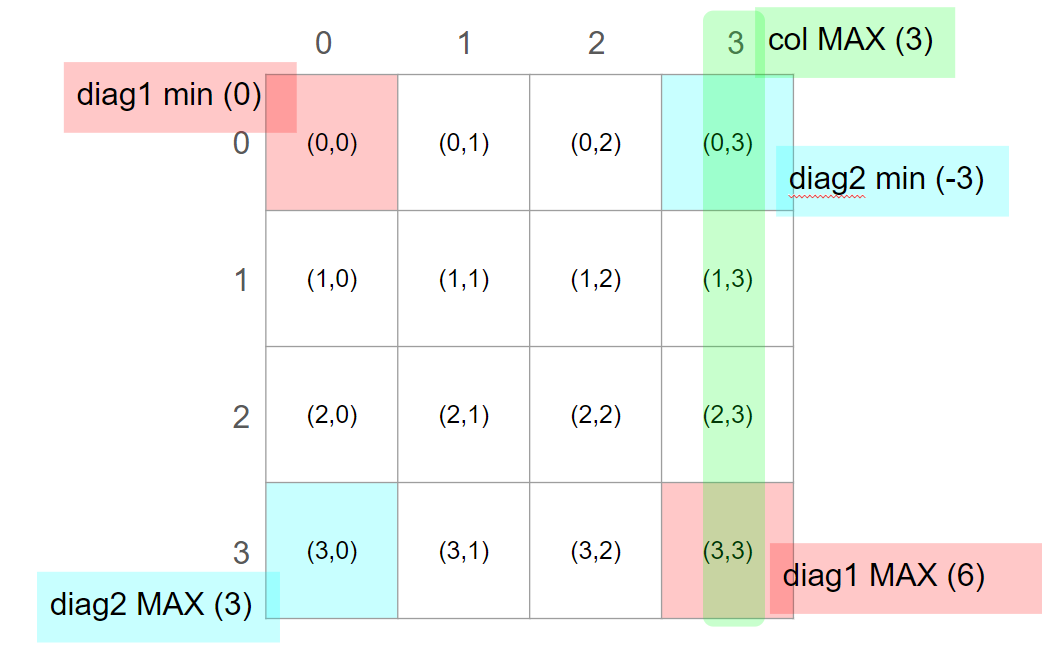
column은 col배열, 합을 통해 구분하는 대각선 방향은 diag1, 남은 대각선 방향은 daig2로 구분했다.
이때 col의 최댓값은 $n-1$, diag1의 최댓값은 $2(n-1)$, diag2는 $-n+1$부터 $n-1$까지의 범위를 갖는다.

diag2는 음수가 발생하므로 값 자체를 인덱스로 사용하지 못한다. 따라서 항상 $n-1$을 더하여 $0$부터 $2(n-1)$까지의 범위를 갖도록 조정한다.

이 문제는 n이 9로 한정되므로 masking 배열의 size를 상수로 작성했다.

Solution

int cnt;
int size;
int col[9];
int diag1[17];
int diag2[17];


void checker(int row){
    if (row==size) cnt++;
    else{
        for (int i=0;i<size;i++){
            if (!col[i]&&!diag1[i+row]&&!diag2[i-row+size-1]){
                col[i]=diag1[i+row]=diag2[i-row+size-1]=1;
                checker(row+1);
                col[i]=diag1[i+row]=diag2[i-row+size-1]=0;
            }
        }
    }
}

int totalNQueens(int n) {
    cnt=0;
    size=n;
    for (int i=0;i<9;i++) col[i]=0;
    for (int i=0;i<17;i++) diag1[i]=0;
    for (int i=0;i<17;i++) diag2[i]=0;

    checker(0);

    return cnt;
}

Time Complexity

정확하게 계산해내지 못했다. 매우 rough하게, 최악의 경우 chessboard를 모두 순회하므로 $O(N^2)$으로 예상한다.

지적 및 질문 환영