Intuition
각 원소들의 사용여부에 대해 모든 경우의 수를 따져본다.
Approach
[1,5,11,5] 의 배열을 예시로 들겠다.
전체합의 반인 11을 만들 수 있는지 확인해야한다.
첫번째 원소 1의 경우 사용하지 않게 되면 0을 만들 수 있고, 사용하면 1을 만들 수 있다.
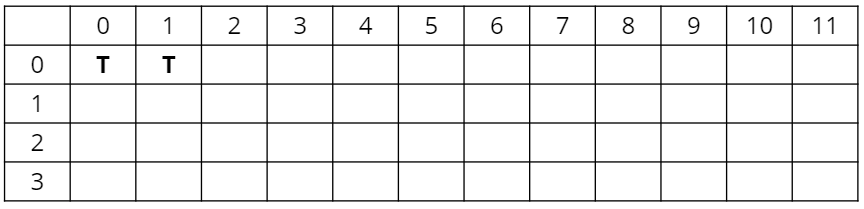
두번째 원소 5를 사용하지 않게 되면, 0 또는 1이 그대로 유지된다.
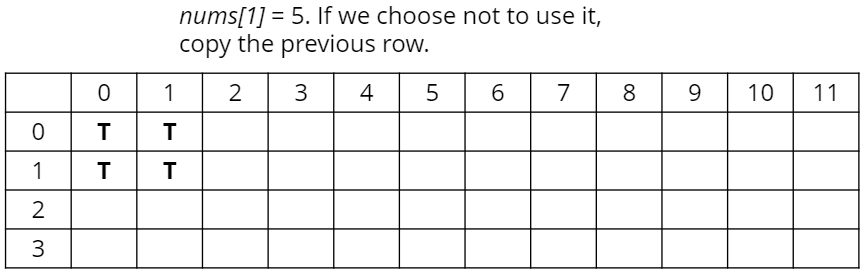
사용하게 되면, 5 또는 6을 만들 수 있다.
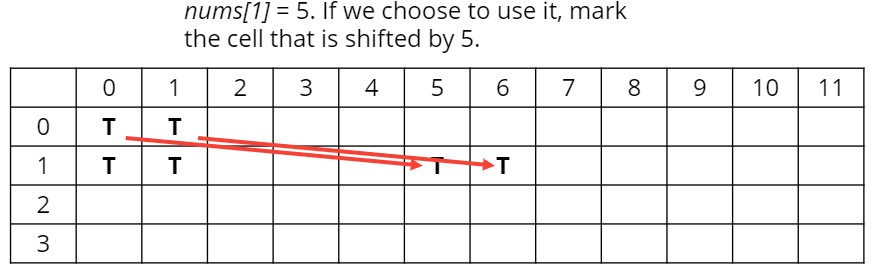
즉, 다음과 같은 점화식을 세워볼 수 있다.
(if, or )
위와 같은 방법으로 마지막 원소까지 확인해준다. 이때, 합이 11을 초과하는 경우는 굳이 살펴볼 필요가 없다.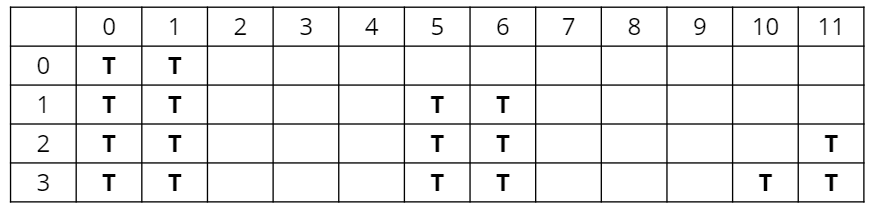
2차원 배열에서 1차원 배열로
i가 증가할 때, i-1때 T였던 값은 i일때도 T이다.
따라서, 2차원 배열 대신 1차원 배열로 좀 더 간단하게 처리해볼 수 있다.
이전에 True 였던 값들을 따로 유지시켜줄 필요가 없기 때문에, 점화식 또한 간단해진다.
(if )
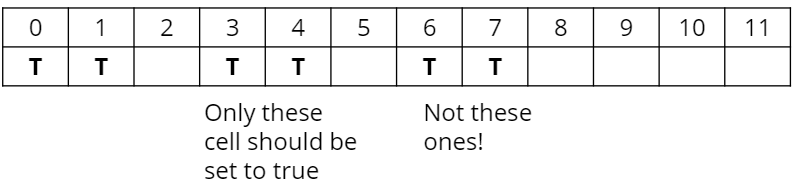
이때, 주의할 점은 j를 뒤에서부터 살펴보아야 한다는 점이다.
예를 들어 인 경우에는 3과4는 0과 1을 통해 true임을 확인할 수 있다.
그러나 여기서 먼저 true로 표시를 하게되면 6과 7에서도 3과4로 인해 true로 계산된다.
Solution
#include <stdlib.h>
bool canPartition(int* nums, int numsSize) {
int sum=0;
for(int i=0;i<numsSize;i++) sum+=nums[i];
if (sum%2) return 0;
int half=sum/2;
int* ans=(int*)malloc(sizeof(int)*(half+1));
for(int i=0;i<=half;i++) ans[i]=0;
ans[0]=1;
for(int i=0;i<numsSize;i++){
for(int j=half;j>=nums[i];j--){
if(ans[j-nums[i]]) ans[j]=1;
if(ans[half]) return 1;
}
}
return 0;
}Complexity
Time Complexity

우선 기본적으로 바깥의 for문은 N번, 안쪽의 for문은 half-nums[i]번 반복된다.
이때, nums배열의 최댓값을 K라고 하겠다.
worst case에 대해 계산하므로 half는 NK가 된다.
따라서 로 표현할 수 있다.
"worst case에 대해 계산하므로 half는 NK가 되어 안쪽 for문은 NK-K번 반복되는 것 아닌가?"라고 생각했지만->교수님께서 이부분에 대해 언급x
Space Complexity
ans배열을 half만큼 추가로 생성한다.
