Intuiton

longest와 subsequence의 키워드로 DP풀이를 고려해볼 수 있다.
text1과 text2의 문자를 하나씩 비교하며 같을 때마다 Longest Common Subsequence(이하 LCS)의 길이가 +1될 것이라고 예상했다.

Approach

문제 재정의 및 목표 설정

먼저 subproblem을 아래와 같이 정의한다.

$A[i][j] :$ text1$[0:i]$ 와 text2$[0:j]$에서의 LCS

자연스럽게 최종적으로 구해야하는 목표는 아래와 같이 작성할 수 있다.

Goal : $A[$strlen(text1)$-1][$strlen(text2)$-1]$

점화식 구하기

text1 : fbdk, text2 : kdk 인 input을 가정해보겠다.
text1에서 f, text2에서 k를 가져왔을 때 공통되는 문자가 없으므로 lcs는 0이다.
text1에서 fbdk, text2에서 k를 가져왔을 때, 문자 'k' 하나가 공통되므로 lcs는 1이다.

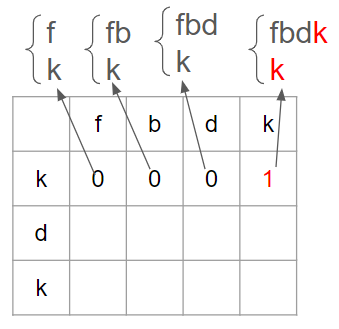
text1에서 fbd, text2에서 kd를 가져왔을 때, 문자 'd' 하나가 공통되므로 lcs는 1이다.

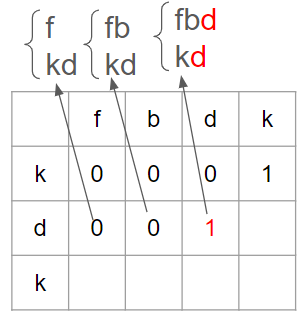
1에서 fbdk, 2에서 kd를 가져왔을 때, subsequence d 또는 k 가 공통되므로 여전히 lcs는 1이다.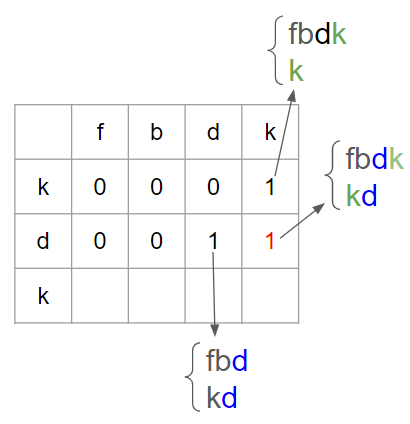즉, 위와 같이 두 문자가 일치하지 않는 경우에는 위쪽($A[i-1][j]$)나 왼쪽($A[i][j-1]$) 의 값을 $A[i][j]$에 할당시켜줘야 함을 알 수 있다.
지금의 경우 위쪽, 왼쪽 모두 lcs가 1이지만 값이 다를 경우에는 더 큰 값을 할당시켜주면 되시겠다.

계속해서,
1에서 fbdk 2에서 kdk를 가져왔을 때, subsequence dk로 lcs는 2가 된다.
이때, 기존의 fbd 와 kd에서 'k'라는 공통된 문자가 추가되면서 common subsequence의 길이가 연장되는 것으로 이해할 수 있다.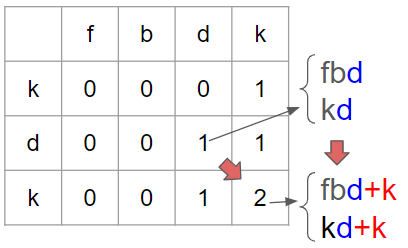
즉, 아래와 같이 점화식을 작성해 볼 수 있다.

$A[i][j]=\begin{cases} A[i-1][j-1] + 1\quad(t1[i]==t2[j])\\ MAX(A[i-1][j], A[i][j-1])\quad(t1[i]!=t2[j])\\ \end{cases}$

꼭 대각선이어야 하는가?

문득 이런생각이 들 수 있다.
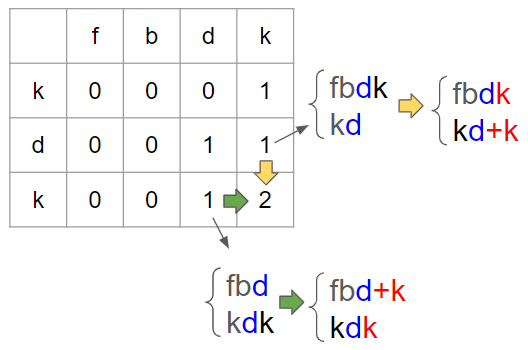예를 들어 위쪽의 경우, 기존의fbdk와 kd인 상태에서 text2에만 k가 추가적으로 붙으면서 common subsequence가 +1이 된다라고 생각할 수 있다. 그러나 이 경우에는 대각선, 위, 왼쪽의 값이 같으면서 우연히 답이 같을 뿐이다.

아래와 같이 중복된 문자의 예외를 고려하지 못하는 것을 확인할 수 있다.

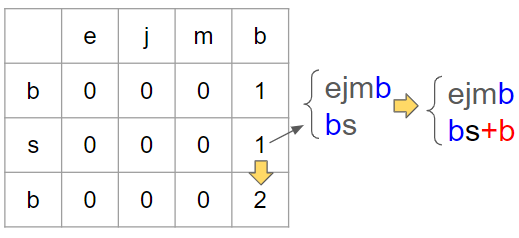
패딩 넣기

점화식을 살펴보면 i-1과 j-1을 참조함을 알 수 있다.
따라서 i와 j를 단순히 0부터 시작하게 되면 out of bound error를 범하게 된다.
이를 방지하기 위해 배열의 가로세로에 패딩을 적용시켜준다.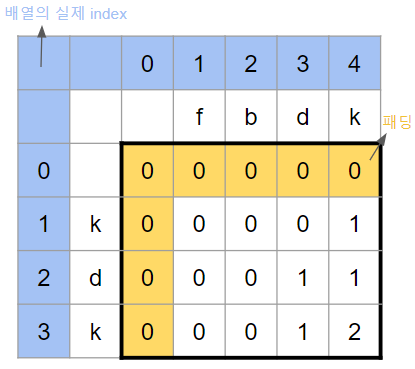배열의 [1][1]부터 채워줘야 하므로 점화식의 A배열 인덱스 변수i, j에 +1씩을 해준다.

$A[i+1][j+1]=\begin{cases} A[i][j] + 1\quad(t1[i]==t2[j])\\ MAX(A[i][j+1], A[i+1][j])\quad(t1[i]!=t2[j])\\ \end{cases}$

Solution

#include <string.h>
#define MAX(a,b) ((a)>(b)?(a):(b))

int arr[1001][1001];

int longestCommonSubsequence(char* text1, char* text2) {
    int t1Len=strlen(text1);
    int t2Len=strlen(text2);

    for (int i=0;i<t1Len;i++){
        for (int j=0;j<t2Len;j++){
            if (text1[i]==text2[j]) arr[i+1][j+1]=arr[i][j]+1;
            else arr[i+1][j+1]=MAX(arr[i][j+1],arr[i+1][j]);
        }
    }

    return arr[t1Len][t2Len];
}

Time Complexity

t1Len=N, t2Len=M 이라고 할 때, $O(NM)$이다.