[파이썬] 막대그래프 + 꺾은선그래프 + 범례

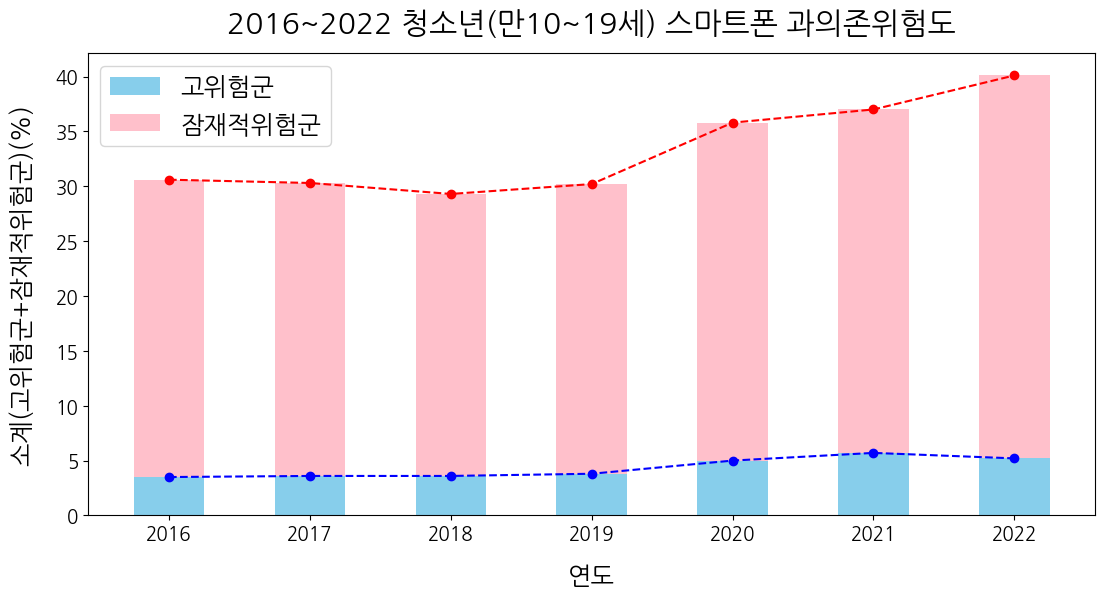
💡 내가 만들고자 하는 막대그래프 + 꺾은선그래프

---

0. 미리 작업해 놓은 데이터프레임

dfsm3

시점	고위험군	잠재적위험군
2016	3.5	27.1
2017	3.6	26.7
2018	3.6	25.7
2019	3.8	26.4
2020	5	30.8
2021	5.7	31.3
2022	5.2	34.9

1. 막대그래프 + 꺾은선그래프

plt.figure(figsize=(15,10))

plt.bar(dfsm3.index, dfsm3['고위험군'])
plt.bar(dfsm3.index, dfsm3['잠재적위험군'], bottom=dfsm3['고위험군'])

plt.plot(dfsm3.index, dfsm3['고위험군'], color='skyblue', linestyle='-', marker='o')
plt.plot(dfsm3.index, dfsm3['잠재적위험군'], color='pink', linestyle='-', marker='o')

plt.show()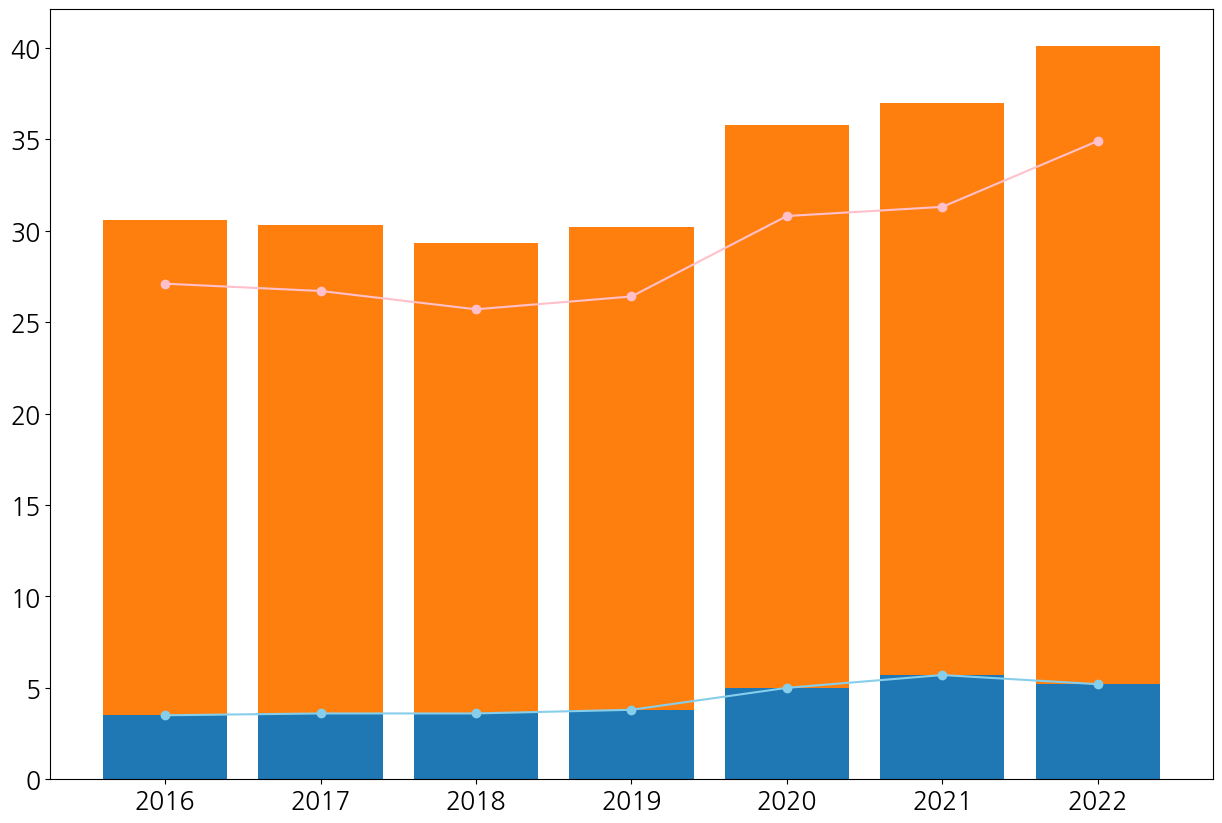

😭 어려웠던 점

핑크색 꺾은선그래프의 값이 주황색 막대그래프 값과 달라 너무 당황스러웠고 내가 코드를 잘못 작성한 줄 알았다. 사진의 막대그래프는 bottom=dfsm3['고위험군']으로 누적그래프가 되어 있는 상태이다. 반면 핑크색의 꺾은선그래프는 누적이 안 된 상태이므로 잠재적위험군의 막대그래프의 값과 위치가 다를 수밖에 없다. 그래서 plt.plot(dfsm3.index, dfsm3['잠재적위험군'], bottom=['고위험군'], color='pink', linestyle='-', marker='o'로 작성해보았지만 오류가 났다. 꺾은선그래프는 막대그래프와 달리 위로 누적해서 쌓는 그래프가 아니기때문인 것 같다. 그래서 생각해 낸 방법이 원래의 잠재적위험군 값에 고위험군 값을 더하는 것이다. 왜냐하면 막대그래프는 누적되었기 때문이다.

---

1. 데이터프레임 리스트로 추출(딕셔너리로 변환 후 가져오기)

• 컬럼명 ➡️ 키 값
• 데이터 ➡️ 리스트로 저장

1. 딕셔너리로 변환

dfsm3_dict = dfsm3.to_dict()
dfsm3_dict

{'고위험군': {'2016': 3.5,
'2017': 3.6,
'2018': 3.6,
'2019': 3.8,
'2020': 5,
'2021': 5.7,
'2022': 5.2},
'잠재적위험군': {'2016': 27.1,
'2017': 26.7,
'2018': 25.7,
'2019': 26.4,
'2020': 30.8,
'2021': 31.3,
'2022': 34.9}}

2. 리스트로 추출

dfsm3_val = dfsm3_dict['고위험군'].values()
dfsm3_val

dfsm3_list = list(dfsm3_val)
dfsm3_list

dict_values([3.5, 3.6, 3.6, 3.8, 5, 5.7, 5.2])

[3.5, 3.6, 3.6, 3.8, 5, 5.7, 5.2]

➕참고 사이트 | 데이터프레임 리스트로 추출

2. 막대그래프 + 꺾은선그래프

plt.figure(figsize=(13,6))

plt.bar(dfsm3.index, dfsm3['고위험군'], label='고위험군', width=0.5, color='skyblue') #width default: 0.8
plt.bar(dfsm3.index, dfsm3['잠재적위험군'], bottom=dfsm3['고위험군'], label='잠재적위험군', width=0.5, color='pink')

plt.xlabel('연도', labelpad=15)
plt.xticks(fontsize=13.5)

plt.ylabel('소계(고위험군+잠재적위험군)(%)', labelpad=15)
plt.yticks(fontsize=13.5)

plt.title('2016~2022 청소년(만10~19세) 스마트폰 과의존위험도', pad=15)

plt.legend()

plt.plot(dfsm3.index, dfsm3['고위험군'], color='b', linestyle='--', marker='o')
plt.plot(dfsm3.index, dfsm3['잠재적위험군']+dfsm3_list, color='r', linestyle='--', marker='o')

plt.show()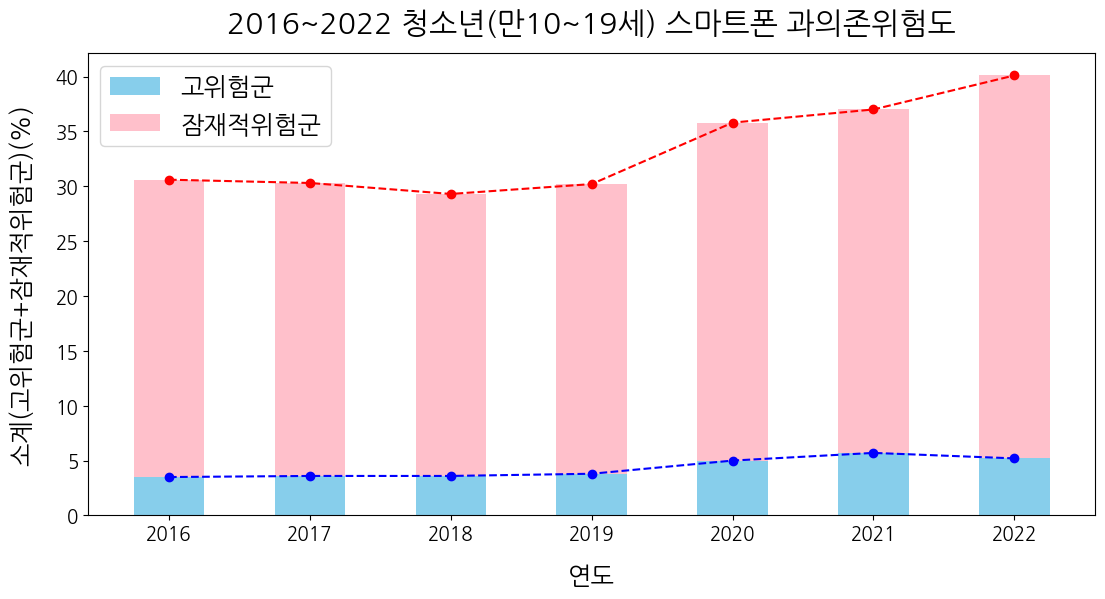

💡 떠오른 아이디어

지금 생각해보니까 '고위험군'과 '잠재적위험군'을 더한 값이 엑셀 파일에 있었다. 더한 값을 '소계'라고 하는데 애초에 이 값을 데이터프레임을 재구성할 때 추가하여 빨간색 꺾은선그래프로 표시했으면 굳이 데이터프레임을 딕셔너리로 변환해서 리스트로 출력할 필요가 없었을 것이다.

---

0. 미리 작업해 놓은 데이터프레임

dfsm3

시점	소계	고위험군	잠재적위험군
2016	30.6	3.5	27.1
2017	30.3	3.6	26.7
2018	29.3	3.6	25.7
2019	30.2	3.8	26.4
2020	35.8	5	30.8
2021	37	5.7	31.3
2022	40.1	5.2	34.9

1. 막대그래프 + 꺾은선그래프(수정한 코드만, 나머지는 동일)

plt.plot(dfsm3.index, dfsm3['소계'], color='r', linestyle='--', marker='o')

💡 떠오른 아이디어2

만약 엑셀 파일에 합계가 없다면 어떻게 하면 좋을까? 각 행의 값을 sum() 함수를 사용하여 더한 값을 구하고 데이터프레임에 추가하면 되지 않을까?

---

0. 미리 작업해 놓은 데이터프레임

dfsm3

시점	고위험군	잠재적위험군
2016	3.5	27.1
2017	3.6	26.7
2018	3.6	25.7
2019	3.8	26.4
2020	5	30.8
2021	5.7	31.3
2022	5.2	34.9

1. 각 행 값의 합계를 구한 후 데이터프레임으로 만들어 기존의 데이터프레임에 추가

dfsm3 = dfsm3.assign(소계=dfsm3.sum(axis=1))
dfsm3

시점	고위험군	잠재적위험군	소계
2016	3.5	27.1	30.6
2017	3.6	26.7	30.3
2018	3.6	25.7	29.3
2019	3.8	26.4	30.2
2020	5	30.8	35.8
2021	5.7	31.3	37.0
2022	5.2	34.9	40.1

2. 막대그래프 + 꺾은선그래프(바로 위의 그래프 구하는 코드와 동일)

😮 새롭게 알게 된 점 + 추가적으로 공부해야 할 점

직전 게시물과 비교해볼 때 .drop() 에서는 axis=0이 행이고 axis=1이 열인데 .sum()에서는 axis=0이 열이고 axis=1이 행이다. 사실 왜 이렇게 되는지는 모르겠다.. 이는 추가적으로 나중에 공부하거나 교수님께 여쭈어봐야겠다.

➕참고 사이트 | axis를 사용한 .sum()과 .drop() 예제, axis의 의미

---

⭐ .sum()과 .drop()에서 axis=0과 axis=1의 의미 차이

arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
arr

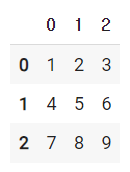
df = pd.DataFrame(arr)
df

변수 arr의 output	변수 df의 output

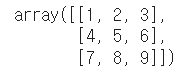#sum
print(df.sum(axis=0)) #세로(열) 합
print(df.sum(axis=1)) #가로(행) 합

#sum의 output	axis의 의미	해설
	axis은 방향성을 나타냄 axis=0 ➡️ 행 방향성(위 → 아래) axis=1 ➡️ 열 방향성(왼쪽에서 오른쪽)	df.sum(axis=0) ➡️ 위에서 아래로 12(=0+4+7) 15(=2+5+8) 18(=3+6+9) df.sum(axis=1) ➡️ 왼쪽에서 오른쪽 6(=1+2+3) 15(=4+5+6) 24(=7+8+9)

#drop
print(df.drop(0, axis=0)) #가로(행) 삭제
print('\n')
print(df.drop(0, axis=1)) #세로(열) 삭제

#drop의 output	axis 의미	해설
	axis은 방향성을 나타냄 axis=0 ➡️ 행 방향성(위 → 아래) ⭐연산의 의미로 행을 drop axis=1 ➡️ 열 방향성(왼 → 오) ⭐연산의 의미로 컬럼을 drop	df.drop(0, axis=0) ➡️ 위에서 아래로 0행 삭제 df.drop(0, axis=1) ➡️ 왼쪽에서 오른쪽 0열 삭제