
7-1. 들어가며
학습 목표
- 금융 시계열에서만 나타나는 특징이 무엇이 있는지 파악하기
- 금융 시계열 모델 알아보기 : ARCH, GARCH
7-2. 금융 시계열의 특징
용어 정리
- factors(팩터)
- 투자 자산의 전체 구성 성분 요소
- Return(수익률)
- 자본에 대한 수익 비율
- 투자 수익성 지표로 활용
- Multiperiod Simple Return(다기간 수익률)
- 단일 보유 기간 동안 수익률 -> 여러 기간으로 나타냄
- Multiperiod Log Return(다기간 로그 수익률)
- 다기간 수익률의 log값 적용(계산에 용이)
금융 분야의 Stylized Fact
- Finance에는 자산 Price 자체보단 -> 수익률 즉, Return에 대해 더 높은 관심을 보임
수익률들 간의 관계 -> 연관 없음
- 효율적 시장 가설(EMH)
- 약형 효율적 시장 : 정보가 가격에 즉각 반응하지 않지만, 공개 정보는 포함
- 준강형 효율적 시장 : 정보의 공개 순간 즉각 가격 반영
- 시계열 분석과 같은 과거 정보 투자 전략으로는 초과수익률 얻기 어려움
- 내부자 정보로만 초과 수익률이 가능한 구조
- 강형 효율적 시장 : 모든 정보가 발생 즉시 가격에 반영
- 어떤 방법을 써도 초과 수익률 얻는 것은 불가능
금융에서 활용되는 수익률(Return)
수익률 평가 지표 알아보기
인자값() : 각 시점 가격
- 다기간 수익률(Multiperiod Simple Return)
- 다기간 로그 수익률(Multiperiod Log Return)
- 연속된 기간 수익률 계산 시 : 로그 수익률이 Additive하게 적용되어 용이
- *Additive : 다른 factor(요인)들과 결합될 경우, 보통 경우보다 누적 효과 및 강도가 좋아지는 것
S&P 500
-
미국 신용평가사 S&P Global이 미국에 상장된 시가총액 상위 500개 기업 주식들을 지수로 묶어서 발표하는 미국 3대 증권 시장 지수 중 하나(위키피디아)
-
S&P 500 daily Return
- 10년간의 Return 히스토그램
- 정규분포에 비교 -> 오른쪽으로 Long-tailed 되어 있음 + 정점이 더 높음
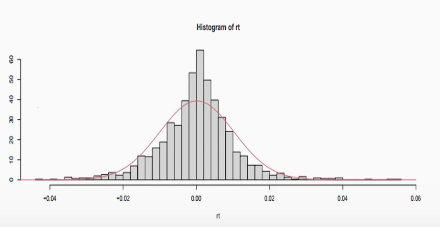
- 정규분포에 비교 -> 오른쪽으로 Long-tailed 되어 있음 + 정점이 더 높음
- 10년간의 Return 히스토그램
자산의 수익률(Asset Return)에 대한 주요한 경험기반의 사실들(stylized fact)
- 경험기반의 사실(stylized fact)
- 과거에서부터 지금까지 축적된 정형화된 사실 기반 접근 방법론
- 좌우 대칭 분포(symmetric distribution)
- 정규분포처럼 좌우가 대칭인 경우
- 두꺼운 꼬리 분포(Heavy-tailed distribution)
- 지수함수보다 느리게 감쇠되는 꼬리를 가짐
- 정규분포보다 꼬리가 두꺼운 경우임
- 평균 중심으로 좌우 대칭을 보이나, 굉장히 두꺼운 꼬리 분포를 따름
- 단기간 대박 혹은 쪽박이 있음
- 단기간 대박 혹은 쪽박이 있음
- 각 시점 수익률 -> 서로는 별 관계 없음
효율적 시장 가설(EMH): 주식 가격은 이용가능한 정보를 즉각 정확히 반영- 과거 데이터 혹은 패턴을 분석해도 ➡️ 미래 수익률 예측은 불가능
- 수익률 간 독립성이 있다는 표현
- 수익률 제곱 간에만 높은 관계 존재!
조건부 이분산성(Conditional Heteroskedasticity): 자산 수익률 분산(제곱과 같은 의미)의 경우 상수가 아니어서 변동성이 크고 일정하지 않기 때문에 -> 자기회귀적 특성을 가지고 있음!- 과거의 높은 변동성 즉, 분산이 ➡️ 미래 변동성에 영향을 끼치는 것
- 자기 회귀적 특성을 갖는다는 의미 : 금융 시장의 클러스터링 효과 즉, 특정 시점의 변동성이 발생한 후에도 한동안 높은 변동성이 지속되는 것
7-3. 금융 시계열을 위한 모델, ARCH
용어 정리
- S&P 500 returns
- 미국 상장 시가총액 상위 500개 기업 주식을 모아서 만든 지수
- IBOVESPA returns
- 브라질 주식 시장에서 거래되는 주요 기업 주식을 모아서 만든 지수
- Volatility Modeling(변동성 모델링)
- 변동성 예측 모델링
- ARCH
- 변동성 예측 모델
- 시간에 따라 변하는 변동성 + 변동성 클러스터링
- GARCH
- ARCH 파생 모델
- 오차 분산에 대한 ARMA 가정 모델
- Cluster
- 시계열 데이터의 시각화 시, 특정 기간 이후 충격이 나타나는 현상
- 충격이 일정 기간 유지되는 것
S&P 500 returns & IBOVESPA returns
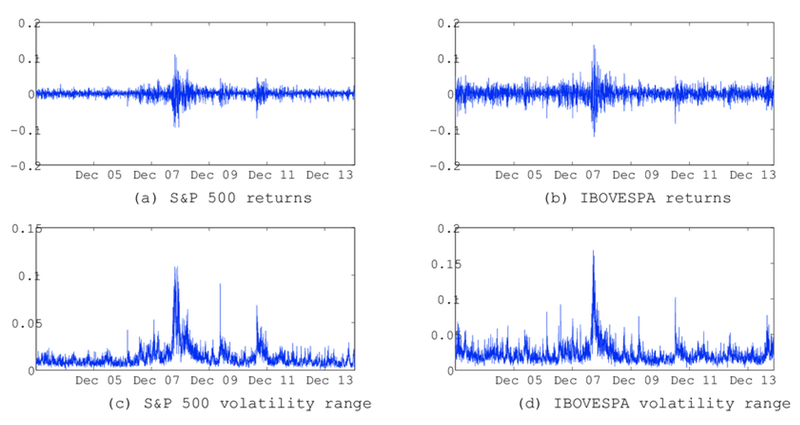
- 수익률 변동성이 높아지는 시기를 살펴보면 -> 하나의 cluster처럼 뭉쳐 있음
- 변동성에 대한 AR 모델 적용 가능성 있음
- ACF, PACF plot으로 유의미한 Lag 확인
ARCH
- 자기회귀 조건부 이분산성 모델
- Auto Regressive Conditional Heteroskedasticity Model
ARCH(m)- 자산 변동성을 자기 회귀를 통해 모델링
arch라이브러리로 바로 활용 가능
GARCH
- 일반화 자기회귀 조건부 이분산성 모델
- Generalized AutoRegressive Conditional Heteroskedasticity Model
- 자산 변동성에 AR, MA 같이 적용 -> 높은 수준의 변동성 예측 가능
GARCH(p,q)- p, q 2개의 파라미터
- GARCH(1,1)의 일반식
변동성에 대한 AR 모델 적용 가능성
- Nasdaq(나스닥) 변동성(수익률 제곱)의 ACF 및 PACF plot 적합
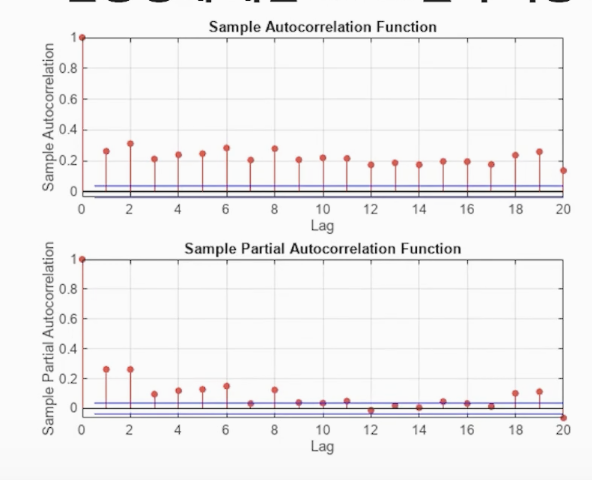
변동성 모델링이 가능하게 해주는 것
- 자산 변동성이 중요한 경우
- 파생상품 가치측정, 위험관리 부문 ➡️ ARCH, ARCH 모델 중요성 높음
- 트레이딩 측면에서도 중요
- GARCH 파생 모델
- S-GARCH, E-GARCH 등
- GARCH 파생 모델
