Day 01. 기초 통계와 탐색적 데이터 분석

1. 통계학의 중요성

• 통계학
  • 모집단 정보를 알기 위해 표본(샘플)로 추론
  • 모집단 전수 조사에는 시간과 비용 과다 발생

• 데이터 분석과 통계 분석의 유사성
  • 모집단에 준하는 빅데이터 소유가 가능해져, 데이터 처리/분석 직군이 만들어짐!

• 데이터 직군 변화
  • 현실적으로는 "데이터 잡부"
    • 데이터 전처리
    • 데이터 모델링
    • A/B test
    • 모델 서빙

• 통계 관련 Tool
  • SAS
    • 헬스케어(FDA, 식약처), 금융권에서 사용하는 상용소프트웨어
    • 유료툴 -> 다른 무료툴 등장으로 약해짐
      • 1 copy 당 몇 천만원..
  • R
    • 통계학과에서 사용
    • Rstdio(인터페이스 툴) 사용
    • 무료, 그러나 딥러닝 오픈소스는 조금 약함
  • Python
    • 코딩 장벽은 있으나 활용성이 좋음 <-> 러닝 커브가 높음
    • 무료

• 강의 모듈
  • Pandas, Matplotlib, seaborn 복습
  • Numpy : 선형대수, 분포
  • Scipy : 통계 검정
  • Statsmodel : 회귀분석, 시계열분석, 분산 분석(ANOVA) 등의 통계툴

• 패키지 디렉터리 정리 해보기!
  • 사용하는 패키지의 내용을 아는 것도 중요

• 통계학과 전공 로드맵 참고(서울대학교)
  • 모두 학습하기에는 무리가 있음
  • 탑다운 방식을 사용해야하니, "통계학", "확률 개념 일부", "회귀 분석 및 실습", "표본 설계 및 조사 실습", "생존 자료 분석 및 실습"을 위주로 학습!

• 통계학 학습 방법
  • 쉬운 책 학습(ex. 데이터 과학을 위한 통계)
  • 유튜브 구독(ex. Data scientist 이지영)
  • 최소한의 수식 읽어볼 것(ex. 인하대 통계학 책)

책 추천 링크

• 학습 해결 방법
  • 기술이나 방법적인 어려움이 있을 경우
    • 공식 문서
    • 손으로 작성 -> 보고서 작성!
  • 비즈니스 적용
    • 비즈니스 캔버스 : 회사 사업구조를 파악해서 데이터가 적용될 부분을 파헤침
    • 타 직군과 "함께" 일하기 ➡️ 커뮤니케이션하면서 같이 프로젝트해야 유의미!

2. 데이터 분석과 통계

• 데이터 분석을 왜 해야해?
  • 휴리스틱(경험적 의사결정)
    • 근거 기반 판단이 필요!
  • 데이터 정보 획득을 위한 과정이 쉬워졌다.
    • 저장 비용⬇️, 처리 능력⬆️, 클라우드 시스템

• 데이터 분석이 "필요 역량"인 이유
  • 새로운 개념이 아니고, 회사나 상황에 따라 사용하기 때문
  • 누구나 쉽게 적용할 수 있기 때문에 -> 도메인 지식이 있어야 분석이 유의미해짐!

• 데이터 분석의 현실적 적용
  • 데이터 분석 : 집계(Pivot), 시각화, 통계 분석, 머신러닝/딥러닝

• 기술통계 vs 추론통계 vs 머신러닝

  • 기술통계

    • 요약 및 설명의 방법
    • 평균, 표준편차, 집계, 시각화
    • 데이터 엔지니어링으로 집계 및 Showing하는 것에 초점
    • 논쟁 여지가 적음

  • 추론통계

    • 데이터 표본으로 모집단의 특성 추정
    • Z검정, t검정, a/b test

  • 머신러닝 / 딥러닝

    • 예측력을 높이는 것이 초점!

• 통계의 중요성
  • 데이터 리터러시(Data Literacy) : 데이터 문해력

• 기술 통계 필요요소

  • 데이터의 올바른 가져오기
  • 가져온 데이터의 적절한 집계 및 시각화
  • 위의 2개 방해요소가 편향

  통계적 편향	인지적 편향
  샘플링 편향	확증 편향
  선택 편향	대표성 편향
  생존 편향	후광 효과
  측정 편향

통계적 편향

• 샘플링 편향

  • 다이제스트사 예시
    • 최대한 많은 N수에 집중
  • 갤럽 예시
    • 2000명 정도를 대상으로 격주 여론 조사 -> 승리 예상에 성공

• 선택 편향

  • 연구 대상이 특정 특성을 가지고 있다!
  • 리뷰(대부분 만족스러운 경우 리뷰를 남기기 때문)
    • 부정적 이슈는 과소평가됨

• 생존 편향

  • 선택을 통과한 데이터에 집중하게 됨 -> 미통과 데이터를 간과
  • 비행기에 총탄이 맞이 피격된 곳(몸통)에만 보완 -> 실제로 돌아오지 못한 비행기는 날개의 문제로 돌아오지 못했음!
  • 주식 분석 : 상장 기업만 분석(상장 폐지 기업은 주식장에 없어서 편향 발생)

• 측정 편향

  • 데이터 수집 과정에서 -> 오류가 발생 -> 편향 발생
    • 간이측정기 값에만 의존해서, 방사능 유출 위험이 없다고 잘못 판단해 체르노빌 사태 발생

인지적 편향

• 확증 편향
  • 자신의 믿음 혹은 가설을 강화한 정보만 선택하는 것
• 대표성 편향
  • 특정 범주에 속한 가능성만 과시
• 후광 효과
  • 대상의 한가지 특징 -> 전체 평가에 영향을 미침

3. 중심 경향치와 산포도

• 통계?
  • 집단으로 얻은 자료로 집단 특성을 이해
  • 관심있는 변수 : 결과, Y, 종속 변수
  • 설명하는 변수 : 원인, X, 독립 변수

• 용어
  • 종속변수
    • == Y, 응답변수
    • 예측하려는 변수
    • Y가 범주형 -> Class, 라벨
  • 독립변수
    • == X, 예측변수, 피쳐, 공변량
    • 종속변수 예측을 위한 변수
  • 모집단(Population)
    • 최종 관심 집단
  • 모수(parameter)
    • 모집단 대표 지표
  • 표본집단(Sample)
    • 임의 선택한 부분 집합
  • 통계량(Statistics)
    • 표본집단 대표 지표

• 데이터 요약
  • 잘 요약된 데이터 : 시각화보다 나을 수 있음
    • 가장 좋은 것은 집계 데이터와 시각화 모두 보여주는 것

• 데이터 종류(수치형, 범주형)
  • 명목형 자료 : ex) 혈액형
  • 순서형 자료 : ex) 학점
  • 이산형 자료 : 두 값 사이 유한한 개수 존재
  • 연속형 자료 : 키 값 같은 것, 두 값 사이 무한 소수 존재 가능

• 중심경향성
  • 범주형 데이터
    • 최빈값 : 가장 많이 등장
  • 수치형 데이터
    • 평균값
    • 중앙값

• 평균이 만능이야?
  • 데이터 도메인에 따라서 적용할 평균이 달라진다!
  • 평균은 극단적인 값이 있으면 대표성이 떨어지므로 중앙값이 더 적절할 수도 있음!

평균 종류

• 산술 평균
  
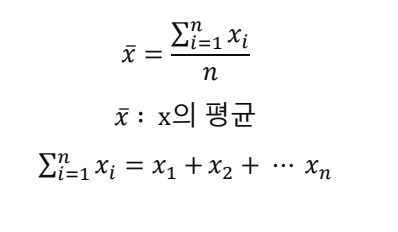
  ex) 가구 소득 = [100, 200, 300, 400, 500]
  -> 평균 가구 소득 = 100+200+300+400+500 / 5 = 400만원

• 기하평균
  
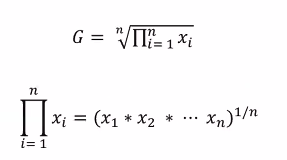
• 증감에 따라서 곱해준 다음 -> 개수대로 나누면 됨
  • ex) $G = (1.1 * 1.8 * 0.95)^{1/3} = 23.4$

• 조화평균
  $2ab \over a+b$

  • 가중 평균과는 다름

  • ex) 12km 비탈면을 v1 = 6km/h로 오르고 2h시간 소요 + v2 = 12km/h으로 오르고 1h시간 소요 = 총 3h 소요

  • 산술평균 : (역산) 24km / (9km/h) = 2.7h-> ❌

  • 조화평균 : (역산) 24km / (8km/h) = 3h -> ✅

  • fl-score

    • Precision / Recall
    • 둘 다 일정 수준으로 높아져야 -> 성능이 올라감!

• 비즈니스
  • 커플 통장
    • 접속률 평균을 구한다면? 남자 접속률 20%, 여성 접속률 80%
      • 산술 평균 : 41%, 조화 평균 : 3.9%

• 산포도

  • 퍼져 있는 정도

  • 표준편차, IQR 등 사용

  • 분산과 표준편차

    • 평균에 대해 데이터의 분포도를 분석 -> 평균을 구해야 알 수 있음!
    • 분산 :
    
    
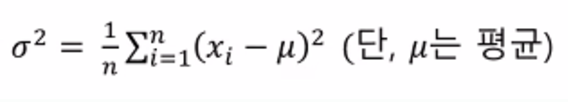
    • 표준편차 :
    
    
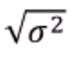
    • 모수 : 모평균(μ, 뮤), 모 표준편차(σ, 시그마)
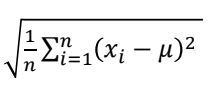
      • 모 표준 편차 :
    
    
    • 통계량: 표본평균($\bar{x}$,엑스바), 표본 표준편차(s,에스)
      • 표본 표준편차 :
    
    

  • 사분위수 범위

    • 자료 개수는 동일한 4개로 나누는 것
    • Q1 : 25%, Q2 : 50%, Q3 : 75%
    • Q1과 Q3 차이 -> IQR
  
  

• 변동계수

  • 평균, 분산 -> 단위 영향 -> 절대 수치로 분산을 알기 어려움
  • 편차와 평균의 비율을 표기 -> 서로 다른 자료형 비교

• 상자 수염 그림
  • 최대값(상한 이상치) : Q3 + 1.5 * IQR
  • 최소값(하한 이상치) : Q1 - 1.5 * IQR

• 표준편차
  • 표준편차를 알면 -> 데이터 분포 정도 파악 가능!

4. 데이터 시각화

• 탐색적 데이터분석(EDA)
  • Python 시각화 라이브러리
    • Matplotlib
    • Seaborn
  • 모든 요소들 == 조정 가능한 객체(제목, 눈금, 축...)
  • matplot : 외부 틀(fig)
  • 그래프(subplot) : seaborn

• Seaborn 시각화 방법 정리

함수명	이름	x축	y축	특징
countplot	막대그래프	범주형 자료형	데이터 개수
barplot	막대그래프	범주형 자료형	수치형 자료형	y축은 평균
boxplot	상자수염그림	범주형 자료형	수치형 자료형	데이터 분포, 이상치 동시 확인
histplot	히스토그램	수치형 자료형	데이터 개수
scatterplot	산점도	수치형 자료형	수치형 자료형

• Countplot : 범주형 자료형의 데이터 개수
  • X축 : 범주형 데이터, Y축 : 데이터 개수
• barplot : 범주형 데이터간 집계 비교
  • X축 : 범주형 데이터, Y축 : 수치형 데이터
• boxplot : (범주형 자료형간) 수치 분포를 비교
  • X축 : 범주형 데이터, Y축 : 수치형 데이터
• histplot : 수치형 변수 -> 데이터 개수 비교
  • X축 : 수치형 데이터, Y축 : 데이터 개수
• scatterplot : 수치형 변수간 분포 확인
  • X축 : 수치형 변수, Y축 : 수치형 변수

5. Numpy.random 모듈

• Numpy
  • numpy array 사용
  • 통계학 : random 함수로 데이터 생성 및 실험에 사용
• Numpy 디렉터리

numpy
|
├── 기본 통계 함수
|   ├── mean()               # 데이터 평균값 계산
|   ├── median()             # 데이터 중앙값 계산
|   ├── std()                # 데이터 표준편차 계산
|   ├── var()                # 데이터 분산 계산
|   ├── sum()                # 데이터 합계 계산
|   └── prod()               # 데이터 곱 계산
|
|
├── 퍼센타일, 백분위 함수
|   ├── percentile()         # 데이터 특정 퍼센타일 값 계산
|   └── quantile()           # 데이터 특정 분위 값 계산
|
|
├── 최소값/최대값 관련 함수
|   ├── min()                # 데이터 최소값 반환
|   ├── max()                # 데이터 최대값 반환
|   ├── argmin()             # 최소값 인덱스 반환
|   └── argmax()             # 최대값 인덱스 반환
|
|
├── 데이터 생성 및 처리 함수
|   ├── histogram()          # 데이터 히스토그램 계산
|   ├── unique()             # 데이터에서 고유값 반환
|   └── bincount()           # 정수 배열 값 빈도 계산
|
|
├── 랜덤 데이터 생성(통계적 실험 시 사용 가능)
|   ├── random.randn()       # 표준 정규분포를 따르는 랜덤 값 생성
|   ├── random.normal()      # 정규분포를 따르는 랜덤 값 생성
|   ├── random.randint()     # 정수 범위에서 랜덤 값 생성
|   └── random.choice()      # 데이터에서 랜덤 샘플 추출

• random 함수

함수	설명	예시
np.random.seed()	난수 생성 초기 값 설정(재현 가능성 보장)	np.seed(42)
np.random.rand()	0~1 사이 균등분포에서 난수 생성	np.random.rand(3,2)
np.random.randn()	표준정규분포 난수 생성	np.random.randn(4)
np.random.randint()	정수 난수 생성	np.random.randint(1, 10, size=5)
np.random.uniform()	균등 분포 난수 생성	np.random.unform(0, 10, size=5)
np.random.normal()	정해진 평균 및 표준편차 -> 난수 생성	np.random.normal(0, 1, size=10)
np.random.choice()	주어진 배열에서 임의값 샘플링	np.random.choice([1,2,3', size=2, replacee=False)

• 정규분포(Normal Distribution)
  • Y축 : 데이터의 밀도
  • X축 : 측정 값
  • 종 모양의 대칭 데이터
  • 추론 통계의 기본
  • 히스토그램 중심을 잇게 되면 -> 유사 정규분포 그래프 그리기 가능!
  • 분포 생성 : 평균과 표준편차로 분포 생성 가능!

전체 실습 링크 : Day1 기초통계(문제)_이하얀(복제)