Day 02. PA와 추론통계

1. Product Analyst 소개

• 하드 스킬에만 집중하지 말고, "서비스의 성장"에 초점을 맞추기
  • 도구는 바뀌어도 조직 가치는 바뀌지 않기 때문

• Product Analyst의 집중 포인트
  • Descriptive Analysis
    • Ad-hoc 분석
    • 리포트
    • KPI 지표
  • Prognostic Analysis
    • 시각화
    • A/B Test

• Data Scientist
  • 필요 여부에 따른 Diagnostic, Predictive 수행

• Product Analysis
  • 제품 관련 데이터 수집과 분석을 통해 제품 개발 및 마케팅을 하는 것
  • ex) 클릭, 장바구니, 구매 등 사용자로부터 발생되는 event

• 그로스 해킹(Growth Hacking)
  • 데이터 기반으로 정의한 "핵심지표"로 "실험"을 통해 배우고, 빠르게 반복하며 "서비스의 성장"을 이루는 것

• Product Analytics Tool
  • 사용자 행동 데이터
    • 웹, 앱에서 유저 행동 기록
    • 클릭, 화면 노출, 스크롤...접속 시점부터 이탈 시점까지 행동 추적
    • tool) GA4, Amplitude, Mixpanel
      
      
  • 믹스패널(Mixpanel)
    • 제품 분석 및 사용자 행동 분석 툴
    • Addon을 쓰면 추가 기능 이용 가능
    • UX/UI가 직관적
      
      
  • Amplitude
    • 올인원 솔루션
    • 가격 문제는 있지만, 그만큼 많은 것을 할 수 있음
    • LTV, Persona 리포트 및 A/B test 가능
      
      
  • Google Analytics 4
    • 세션 및 페이지뷰 기반 마케팅 무료 분석툴
    • 모바일 중심 -> 점점 사용하지 않는 추세
    • UX/UI 복잡
    • 50만 세션 초과 -> 로우데이터 샘플링만 됨(유료툴 사용 권장)

• 데이터 과학자의 할 일
  • 단순 분석만이 아닌 분석환경 구축을 지원해야 함
  • SaaS 서비스 구입 시의 비용 및 장점에 대한 정리가 필요!
    
• 출처 : GA4 vs 믹스패널 vs 앰플리튜드 : 뭐가 다를까요? 차이점 쉽게 이해하기

2. AARRR 프레임워크

• AARRR 분석 프레임워크
  • 서비스 성과 측정 방법론
    • 사용자획득(Acquisition) : 새 고객 획득
    • 활성화(Activation) : 새 고객 활성화
    • 유지(Retention) : 고객 유지
    • 수익(Revenue) : 고객으로부터의 수익 창출
    • 추천(Referral) : 고객이 -> 제품, 서비스 추천

• Acquisition
  • 고객들이 프로덕트에 최초 접속하는 단계
    • 유입 분석(어떤 캠페인을 통해 얼만큼 들어오는지)
  • CAC
    • Customer Acquisition Cost
    • 유저를 획득하는 비용
    • 신규 유저 1명 획득을 위해 필요한 비용 계산
      • $총 지출 비용 \over 신규 유저 수$
  • UTM 파라미터
    • 온라인 마케팅의 효과 측정 변수
    • 캠페인 소스
      • utm_source
      • 웹사이트 도착 직전 장소
      • ex) Google, Naver, Facebook
    • 캠페인 매체
      • utm_medium
      • 유입 경로
      • ex) Email, display, organic
    • 캠페인 이름
      • utm_campaign
      • 어떠한 캠페인인지 여부
      • ex) summer_sale, discount_coupon

• Activation
  • 사용자들이 프로덕트 핵심 가치 경험
  • 회원가입, 상품 조회, 장바구니 담기, 쿠폰 조회수, 좋아요 등
  • 서비스를 어떻게 액티브하게 이용하는지
    
    
  • 예시
    • zoom : 신규 유저들이 Zoom을 통해 화상회의를 하는 습관 형성
    • Netflix : 신규 유저들이 넷플릭스에서 영상을 시청하는 습관 형성
    • 배달의 민족 : 신규 유저들이 배민에서 배달을 시키는 습관 형성
  • 사용자들이 스스로 제품 경험 및 습관화하지 않기 때문에, 사용자들에게 좋은 경험을 제공해야 리텐션을 이끌어 내는 것!
    
    
  • Activation의 개선
    • 초반 사용자들의 핵심가치 습관화
    • 초반 이탈 사용자 감소
    • 더 많은 사용자를 유지
      
      
  • 체류 시간과 전환율
    • 체류 시간(TS) : 프로덕트 내에서 소요한 시간
      • 마지막 페이지 접속 시간 - 첫 페이지 접속 시간
    • 전환율(CVR) : 프로덕트의 제공 가치 도달 비율(사용자가)
      • $상품 구매 수 \over 서비스 총 방문자 수$

• Retention
  • 특정 기간 내 활성화 유저 수
  • 코호트 리텐션 : 동질 특성 또는 경험을 공유하는 집단
  • 리텐션 커브 : 코호트 차드 -> 시간 기준 시각화
  • Day N Retention : 코호트 유저 중 N이라는 날짜가 되는 날 이용자 비율 분석
    
    
  • 코호트 리텐션
    • 코호트 : 동질적 특성 및 경험 공유 집단
    • 같은 시기에 가입한 사용자들을 묶어서 지칭
    • 가입 시기만이 아닌, 성별, 나이, 페르소나 등의 다양한 기준을 통해 코호트 구분
    • 서로 다른 코호트 간의 다른 패턴 분석으로 새 인사이트 도출!
  • 리텐션 커브
    • 코호트 분석 시각화(그래프)

• 실습
  • 날짜형 데이터의 처리
    • event_time -> 01로 바꾸기
    • 유저별 날짜 최소값 -> cohort month로 설정하기
    • cohort index -> "현재 날짜" - "cohort_month"(두 날짜의 차이)

• Day N Retention
  • N째 -> 유지된(Retained) 유저 비율
    • ex) 모바일 게임 첫 플레이 시점 유저 100명(1월 1일) ➡️ 100명 중 7일 뒤 -> 플레이어가 35명 ➡️ Day 7 RetentioReferral의 대표지표n = 35%

• Churn rate(이탈율)
  • 고객의 이탈 비율
  • chourn되는 유저를 막는 것이 중요!
  • ${이탈 유저 \over 전체 유저} * 100$
  • 이탈 유저에 대한 예측 모델링
    • 로지스틱 회귀 : Time not Included
    • Survival Analysis : Time included

• Referral
  • 기존 사용자 추천 또는 입소문으로 새 사용자를 데려오는 것을 말함
  • 친구 초대 유도 및 보상
  • ex) 드롭박스 : 친구 초대 보상으로 추가 저장 공간을 제공, 배민 : 친구 초대로 10,000원 할인 쿠폰 제공

• NPS(Net Promotion Score)
  • 순 구매 추천 지수
  • 추천 고객 비율(%) - 비추천 고객 비율(%)
  • 장점 : 조사 방식이 간단해 리소스 적음
  • 단점 : 어떠한 접점의 경험이었는지 특정 불가, 가중치가 없는 지표

• 바이럴 계수(Viral Coefficient)
  • Referral 대표 지표
  • $유저가 데려온 신규 유저 \over 유저 수$ = $지인 소대 유저 수 * 초대 받아 가입한 유저 수 \over 유저 수$
  • 복리 효과 -> 바이럴 계수가 1 이상이 되면 신규 사용자가 기하급수적 증가!

• Revenue
  • 고객으로부터 얻어내는 수익
  • ARPU(Average Revenue Per User)
    • 활성 유저당 평균 매출
    • $발생한 총 매출 \over 총 활성 사용자(액티브 유저)$
  • ARPPU(Average Revenue Per Paying User)
    • 유료 유저 한 사람 당 결제 금액
    • $발생한 총 매출 \over 총 결제 유저(paid user)$
  • CLV(Customer Lifetime Value)
    • 고객 생애 가치(프로턱트 이용 기간 내 발생시키는 총매출)
    • $CLV = 평균 주문 금액 * 구매 빈도 * 고객 수명$
    • CAC 감소 -> LTV 증가
    • LTV > CAC 유지가 중요
    • ex) 매달 10만원 지출, 1달에 5번 구매, 평균 10년 수명 -> CLV가 6000만원

• 정리

단계	지표
Acquisiton	DAU, MAU, CAC
Activation	체류 시간, 전환율(CVR)
Retention	Retention, 이탈율(Chum Rate)
Referral	NPS, Viral coefficient, 평점, 리뷰
Revenue	LTV, ARPU, ARPPU

3. 추론 통계 소개

• 기술 통계와 추론 통계
  • 기술 통계 : 데이터 특징을 보는 것
  • 추론 통계 : 표본으로부터 모집단 추정

• 빅데이터와 통계의 흐름
  • 고전 통계 : 모집단으로 가정 -> 표본으로 모집단 추정
  • 빅데이터 도입 : 모집단 자체 수집 -> 통계는 필요 없나..?
  • 빅데이터 실제 : 데이터의 질, 적합성 등을 모르는 상태에서 크기만 늘어나는 것은 의미 없음
  • 결국, "추론통계"가 중요하게 됨

• 분포(Distribution)
  • 특정 값 기준으로 중심으로부터 흩어져 있는 정도
  • 경험적 데이터 형태
  • 데이터 요약(중앙값, 평균, 분산 등의 기술 통계량과 퍼진 정도를 시각화)
  • 모집단 추정의 가설 검정 기반
  • 각 분포 -> 특정 확률 함수를 가짐 -> 이것으로 예측!
  • 분포로 현상 모델링 가능(=현실 세계의 추상화, 단순화, 명확화)
  • 즉, 통계 분포를 안다는 것 -> 비즈니스 현상의 설명과 데이터 패턴 설명이 가능하다는 것

• 분포 종류
  • 이산 확률 분포, 연속 확률 분포(데이터가 이산형 값 또는 연속형 값)
  • 통계개론식의 엄격한 증명은 지양하기
    • 수학적 표기법, 용어 정의, 약한 증명까지만(코딩 및 시각화)

• Scipy 모듈

  • Science + Python
  • 통계 분포, 기초 통계 디렉터리(stats)가 별도로 있음

  scipy
  |
  ├── stats                # 통계 분석과 확률 분포 관련 함수 제공
  |   ├── norm             # 정규 분포 관련 함수(PDF, CDF, 랜덤 샘플링 등)
  |   ├── uniform          # 균등 분포
  |   ├── bernoulli        # 베르누이 분포
  |   ├── binom            # 이항 분포
  |   ├── ttest_ind        # 독립 두 표본에 대한 t-검정
  |   ├── ttest_rel        # 대응표본 t-검정
  |   ├── mannwhitneyu     # Mann-Whitney U 비모수 검정
  |   ├── chi2_contingency # 카이제곱 독립성 검정
  |   ├── shapiro          # Shapiro-Wilk 정규성 검정
  |   ├── kstest           # Kolmogorov-Smirnov 검정(분포 적합성 검정)
  |   ├── probplot         # Q-Q plot 생성(정규성 시각화)
  |   ├── pearsonr         # pearson 상관계수 계산
  |   ├── spearmanr        # Spearman 순위 상관계수 계산
  |   └── describe         # 기술 통계량 제공(평균, 표준편차 등)
  |
  

• 균등 분포
  • 두 간격에서의 일정한 확률 함수를 가지는 분포
  • 그래프 아래의 면적 합이 1 -> Y값은 $1 \over b-a$

• 베르누이 분포
  • 확률 변수(X)가 취할 수 있는 경우 -> 2가지
  • 동전의 확률 : 앞면, 뒷면
    • $P(X = x) = p^x(1-p)^{1-x}(where x = 0, 1)$

• 경우의 수
  • 1회 시행 시 일어나는 것이 가능한 사건의 개수
  • Combination으로 표현 : $_nC_x$

• 이항 분포
  • B ~ (n,p)
  • 베르누이 분포의 확장
  • n번의 베르누이 실행 -> x번 성공할 분포
  • 공식 : $P(X = x) = \binom{n}{x} p^x (1-p)^{n-x}, \text{ where } \binom{n}{x} = nC_x$

4. 기본분포

정규 분포(Normal Distribution)

• 가설 검정 기본 분포는 $N \sim(\mu, \sigma^2)$
• 모수 검정 : 많은 검정이 정규 분포를 가정하고 시행되는 것을 뜻함
• 평균 기준 좌우 대칭
  • Y축의 경우는 빈도(확률) -> 전체 면적합(적분값)은 1

• 특징
  • 평균 -> 표준편차 내 데이터 분포도 확인 가능
  • $\mu$ = 1150인 정규분포의 경우(전체 데이터 기준)
    • $\mu$ ± $\sigma$ = 68%
    • $\mu$ ± $2\sigma$ = 95%
    • $\mu$ ± $3\sigma$ = 99.7%

• 첨도(Kurtosis)
  • 확률분포 뾰족한 정도
  • 양수 -> 정규 분포 기준 뾰족, 음수 -> 퍼져있음

• 왜도(skewness)

  • 확률분포 비대칭 정도
    • 웹서비스는 대부분 과금 분포가 right skewness
  • 왜도에 따른 root, log를 이용하면 -> 정규분포 형태로 변형 가능

• 정규 분포의 단점

  • 평균 기준 좌우 대칭, 종 모양
  • 평균 및 표준편차에 따라서 모양이 다양해져 "범위 계산"이 별도로 필요
  • 표준정규분포가 등장하게 된 계기

표준정규분포(Standard Normal Distribution)

• 정규 분포의 일반화(확률 계산) : 평균 0, 표준편차 1
• 모집단 분포를 알 수 있다면 -> 특정 데이터의 백분율 추측 가능
• 표현 :$Z \sim (0, 1^2)$
• 확률 밀도 함수 : $f(x) = {1 \over \sqrt {2\pi\sigma}}e^{(x-\mu)^2 \over 2\sigma^2}$

• 확률 밀도 함수 특징

  • Probability Density of Function
  • 연속 변수 분포 함수
  • 항상 양의 값, 모든 범위의 PDF 합은 1
  
  

• 누적 분포 함수(Cumulative Distribution Function)

  • 특정 값까지의 누적값
  • $F(x) = P(X \leq x)$

• 표준 정규 분포표
  • 주어진 값(z)까지의 누적확률 계산
  • CDF(Cumulative Distribution, Function, 누적분포함수)
    

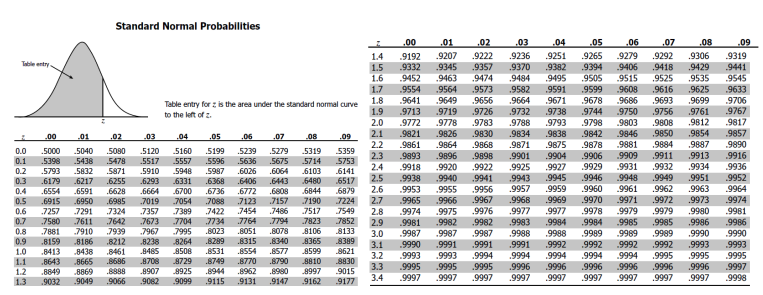
• 표준 정규 분포표 활용
  • 조건 : SAT 평균(μ = 1150), 표준편차(σ = 150) 인 정규
    분포를 따른다.
  • 문제 : 1380점인 사람의 백분율은?
  • Z-Score 이용
    $z=\frac{x-\mu}{\sigma}$ = $1380 - 1150 \over 150$ = 1.53
    • 표준 정규분포에서 0.937 즉, 상위 6.3%

• 정규 분포의 한계
  • 실제 데이터의 경우, 모집단을 모으는 것 자체가 어려울 수 있음
  • 모집단 데이터 수집 불가 == 모수인 평균, 표준편차 역시 알 수 없음

t-분포

• student-t
• 정규분포보다 꼬리 부분이 더 두꺼움

• 자유도

  • 표본 데이터에 계산된 통계량에서 적용

  • 변화 가능한 값의 개수

  • 평균 : 자유도 1개 소요

    • ex) 10개 값으로 이뤄진 표본에서 평균값을 찾으려면 9개의 자유도 값 즉, 데이터 9개 및 평균 1개로 ➡️ 나머지 1개 데이터 추정 가능

  • T분포에 한해 자유도 ≅ 데이터 개수
    
    

  • 자유도 증가 ➡️ t분포가 표준 정규 분포와 근접!

  • 데이터 개수가 30개 이상 ➡️ 정규분포로 가정해 계산 가능

모수와 통계량 표현

• 실제 표본에서의 평균 및 표준 편차는 표현이 다름
  
  
  • Population(모수)
    • 모평균($\mu$) : $\frac{1}{n} \sum_{i=1}^{n} X_i$
    • 모분산($\sigma ^2$) = $\frac{1}{n} \sum_{i=1}^{n} (x_i - \mu)^2$
      
      
  • Sample(표본)
    • 표본 평균($\bar{X}$) : $\frac{1}{n} \sum_{i=1}^{n} x_i$
    • 표본 분산($s^2$) : $\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2$

대수의 법칙(Law of Large Numbers)

• 모평균과 표본평균이 동일
• 표본 집단 크기가 커지면 ➡️ 표본 평균이 모평균에 가까워짐
• 표본을 많이 수집하면 ➡️ 모평균 정확도 상승!

모표준 편차 - 표본표준편차

• n이 아닌 n-1로 나눠줘야 모집단에 더 잘 수렴하는 특징이 있음

불편추정량

• 추정량 기대값과 모수가 같아지는 경우의 추정량
  • Non-biased(불편) : 편향되어 있지 않음을 뜻함
• 빅데이터의 경우에는 n이 충분히 큰 경우, n과 n-1은 동일하게 보기 때문에 중요성이 간과되기도 함

Z검정, t검정

• 대부분 t-test(단일 평균 검정, 서로 다른 집단 검정, 동일 집단 검정)
  • 모분산을 잘 알고 있고 + sample 크기가 30개 이상이라면 ➡️ Z-검정
    • 둘 중 하나라도 만족하지 못하면 t-검정

실습 코드 : Day2_PA와 추론통계(문제)_hayan