Day 03. A/B Test

1. 실험의 종류

• 일반적 데이터 분석
  • 수집이 끝난 데이터로 -> 기술 통계로 현황 파악
  • 대부분 데이터 분석 입문 -> 기술 통계 및 머신러닝 기법을 통한 예측만 집중해서 추론 통계는 간과하는 경우가 많음!

참고

• 기술 통계 : 데이터의 요약
• 추론 통계 : 관측 데이터로 모집단 추정
  ├── 통계적 추론 : 데이터로부터 확률 모형 추론
  └── 가설 검정 : 가설 세우기 + 데이터를 통한 검증

• 실험의 종류
  • 데이터 수집시 인위적 개입 유무로 "관찰 연구", "실험 연구"로 나눌 수 있음
  • 대부분 집계 데이터 분석 -> 관찰 연구 중 "기술통계"
  • A/B Test 같은 앱, 웹 서이브 -> RCT(온라인 통제 실험)

• 용어
  • 처리(Treatment) : 어떤 대상에 주어지는 조건
  • 처리군(Treatment Group) : 특정 처리가 된 대상 집단
  • 대조군(Control Group) : 어떤 처리도 하지 않은 대상 집단
  • 임의화(Randomization) : 처리 적용 대상의 임의 결정
  • 대상(Subject) : 처리 대상

• 관찰 연구
  • 연구자가 변수에 직접 개입하지 않은 상태에서 자연스레 발생하는 데이터를 관찰 및 분석(연구 설계)
  • 특징
    • 연구자 : 데이터 수집 과정에서 변수 통제 없이 관찰 및 기록
    • 역사적 데이터, 연구자 개입이 없었던 수집 데이터
  • 사례
    • 흡연자 및 비흡연자 건강 상태 비교 연구 -> 흡연 여부를 개입하지 않는 것
    • 웹사이트의 사용자들이 스스로 클릭한 광고 -> 효과 분석
  • 장점
    • 윤리적 문제로 인해 실험을 강요할 수 없는 경우, 가능!
    • 비용 및 시간 ⬇️
  • 단점
    • 교란 변수로 인해서 결과 왜곡 가능성 큼
    • 인과 관계의 명확한 규명이 어렵고, 상관 관계만 파악하는 정도로 사용

• 교란 변수(Confounding)
  • 독립 변수, 종속 변수 2가지에 영향을 줌
  • 인과 관계 해석의 방해 요소
  • ex) 당근마켓 : 뱃지 획득 -> 잔존율에 좋은 영향? -> 오류
    • 교란 변수의 고려(애착도, 충성도 등)가 필요

• 인과 추론(Casual Inference)
  • 교란 변수의 관측이 가능한 경우 -> 변수로 넣어 반영
    • 대조군, 실험군에 대한 변수 외의 정보를 동등 관리
    • 회귀 모델 -> 교란 변수를 삽입해 관리

무작위 대조 실험(RCT, Randomized Controlled Trial)

• 의학 통계에서의 약효 검정을 위한 임상 시험에 사용된 것이 대표적
• 웹앱 서비스의 경우, 온라인 통제실험이라고도 함
• 제품 사용자들을 무작위 추출 -> 두 그룹으로 나눔
• 실험군, 대조군으로 나뉜 두 그룹을 균등 비율 5:5로 설정

• 무작위 대조 실험의 정의, 특징, 적용 사례

  • 정의

    • 연구자가 실험 대상을 무작위 두 그룹(이상)으로 배정
    • 한 그룹에는 특정 처치, 다른 그룹에는 처치를 시행을 하지 않고(대조군) 결과 비교

  • 특징

    • 대상자들이 무작위로 실험군 및 대조군에 할당
    • 교란 변수 영향을 최소화하기 위한 조치

  • 사례

    • 신약 임상 시험 : 신약 투여 그룹 및 플라시보 투여 그룹의 건강 개선 정도 비교

  • 웹사이트 A/B 테스트 : 랜딩 페이지 2가지로 무작위 viewing -> 클릭율 비교

• 무작위 대조 실험의 장단점
  • 장점
    • 인과 관계의 명확한 규명
    • 무작위 할당으로 교란 변수 영향 최소화(신뢰성 UP)
    • 대조군 설정을 통해 처치 효과 비교가 명확
  • 단점
    • 실행 비용 및 시간 ⬆️
    • 윤리적 문제도 발생 가능

• 관찰 연구 vs RCT

	관찰 연구	무작위 대조 실험(RCT)
개입 여부	연구자가 직접 개입 X, 내추럴 데이터 관찰	대조군 및 실험군 무작위 할당(개입 O)
인과 관계 규명	명확하지 않음	가능함
교란 변수	제어 어려움(PSM 같은 제어 방법 필요)	제어 가능
윤리 문제	거의 X	발생 가능
실행 비용	비용 및 시간 ⬇️	비용 및 시간 ⬆️
ex	흡연과 건강 관계	임상 시험, 온라인 통제 실험

A/B Test

• RCT의 일종
  • 두 집단의 무작위 배치 + 외부 요인 영향 최소화로 인과관계를 파악할 수 있는 것이 특징

2. A/B Test 사례

• Booking.com
  
  • 첫번째 실험 : 건너뛰기 삭제 -> 진행도 13% 증가
  • 두번째 실험 : 팝업 문구 간략화 -> 진행도 50% 증가

• 넷플릭스 랜딩 페이지
  • 이메일 작성 요소를 통한 퍼널 단계 간소화 실험
  • CTA 버튼 수정으로 테스트
    • TRY IT NOW 문구 강조를 통해 심리적 허들 감소 + 다른 버튼 제거

• 사전 지식

  • Q1. A/B Test 시 수행되는 측정값들은 표본 -> 어떻게 모집단을 대표하는지?

    • A1. 무작위 추출 + 충분한 표본 크기 + 모집단의 다양한 특성을 반영할 수 있는 표본 값이라면 모집단을 대표할 수 있다고 생각

  • Q2. 랜덤화가 무엇인지?

    • A2. 각 참가자나 샘플을 무작위로 실험군이나 대조군에 배정하는 과정, 편향을 없애기 위함!

3. 점추정과 구간추정

점추정(Point Estimate)

• 모수를 특정 수치로 표현

• 모평균 구하는 방법
  • 대수의 법칙에 의해 모평균을 쉽게 추정 가능

구간 추정(Interval Estimate)

• 추정값에 대한 신뢰도 제시를 통해 모수 추정
  
  

• 신뢰 구간(Confidential Interval)

  • 모수 포함 예상 구간

  • 데이터의 전체 95% 포함 구간을 대체로 사용

    • 유의수준(α, Significant Level) : 나머지 5%

  • 모평균의 신뢰도

    • 중심 극한 정리 : n이 충분히 크다면 ➡️ 모집단 분포와 관계없이 표본 평균 분포가 정규 분포에 근사
      • 즉, 모집단이 왜곡 분포여도 n이 크면 정규분포로 가정 가능

  • Z-Score 변환으로 정규 분포를 ➡️ 표준 정규 분포를 따르게!

  • 95% 신뢰 구간 : $\left( \bar{x} - 1.96 \times \frac{\sigma}{\sqrt{n}}, \bar{x} + 1.96 \times \frac{\sigma}{\sqrt{n}} \right)$

• 모분산을 아는 경우($\sigma^2$)

  • 신뢰구간 = $[ \bar{x} - z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}}, \bar{x} + z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}} ]$

• 모분산을 모르는 경우(표준오차로 대체)

  • 신뢰구간 = $[ \bar{x} - t_{\alpha/2, n-1} \times \frac{s}{\sqrt{n}}, \bar{x} + t_{\alpha/2, n-1} \times \frac{s}{\sqrt{n}} ]$

중심 극한 정리

• 임의 데이터 분포를통해 1000개의 데이터 생성(ex. 이항분포)
• 그 중 30개를 뽑아 평균(=표본 평균 생성)
• 위 과정을 500번 반복(=표본 평균 500개)
• 히스토그램으로 정규분포를 따르게 되는지 확인하면 됨

표준 오차(Standard Error)

• 표본 표준 편차
• $\sigma \over \sqrt n$
  • 데이터의 개수가 많고, 표준 편차가 작으면(밀집) -> 오차는 줄어듦

• t분포 기반 신뢰구간
  • 대부분은 모집단 표준편차를 모름 -> t분포로 계산
  • 모집단이 정규 분포를 따름 or 표본 크기가 클 때 사용

부트스트랩(Bootstrap)

• 표본 데이터에서 복원 추출 -> 여러 데이터셋 생성
• 대표적인 모델 : 랜덤 포레스트
  • Bagging
• seaborn에서도 신뢰구간 계산에 부트스트래핑 사용

• t분포 vs 부트스트랩

	t분포 기반	부트 스트랩 기반
조건	정규 분포 or 충분히 큰 표본	분포 가정 없음
계산	공식에 따른 계산	표본 재추출로 시뮬레이션
소규모 데이터	정규분포를 따르지 않는 경우에는 어려움	적용 가능
계산 효율성	빠름	느림

4. 가설검정

• 개념
  • 통계적 가설 검정 : 모집단 특성에 대한 주장이 가설, 표본에서 얻은 정보로 가설의 타당성을 판정
    • 귀무가설을 지지하다가 모순 발견 시 기존 가설을 폐기
    • 가설 : 귀무가설, 대립가설
      • $H_0$(귀무가설) : 실험 및 연구로 기각하려는 가설(현재 믿는 가설)
      • $H_1$(대립가설) : 새로 주장하는 가설

• 용어 정리
  • 검정 통계량(Test Statistics)
    • 가설 검정 목적으로 정의하는 통계량
    • ex) Z-Score
    • $Z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}}$
      
      
  • 유의 수준(Significance level, α)
    • 귀무가설이 참인데도 -> 잘못 기각할 오류 범할 최대 허용 한계
    • 5%
    • 유의 수준 5% == 95% 귀무가설 채택, 5% 경우에만 대립가설 채택
      
      
  • P-value
    • $H_0$이 옳다는 가정, 실제 관측치 혹은 그 이상으로 극단적인 관측치 값을 얻을 확률
    • P-value > 0.05 == 귀무가설 채택, 대립가설 기각
    • P-value < 0.05 == 귀무가설 기각, 대립가설 채택

• 가설 검정 절차
  1. 가설 설정: 귀무가설, 대립가설
  2. 검정 유의수준 결정: 0.01, 0.05, 0.1
  3. 검정분포와 방법 결정: Z-test, t-test, chi-square...
  4. 검정 통계량 계산
     • P-value < 유의 수준
       • Yes : 대립가설 채택
       • No : 귀무가설 채택

• 상황에 따른 검정 방법
  

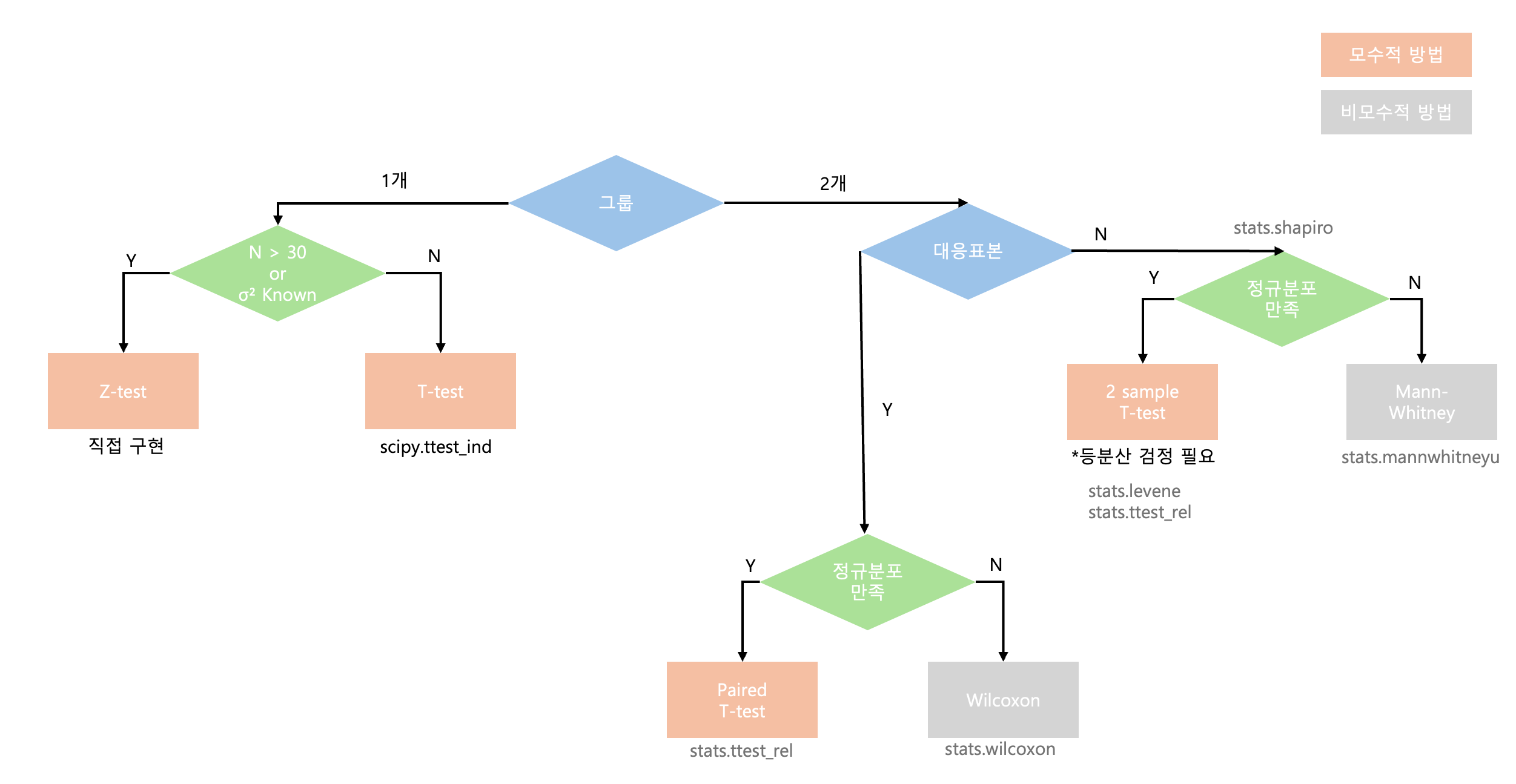
• Scipy-stats 모듈
  • t검정은 있으나 z검정은 직접 수행해야 함

scipy
|
├── stats                   # 통계 분석과 확률 분포 관련 함수 제공
|    ├── norm                 # 정규분포 관련 함수(pdf, cdf, 랜덤 샘플링 등)
|    ├── uniform              # 균등분포
|    ├── bernoulli            # 베르누이 분포
|    ├── binom                # 이항분포
|    ├── ttest_ind            # 독립 두 표본에 대한 t-검정
|    ├── ttest_rel            # 대응표본 t-검정
|    ├── mannwhiteneyu        # Mann-Whiteney U 비모수 검정
|    ├── chi2_contingency     # 카이제곱 독립성 검정
|    ├── shapiro              # shapiro-wilk 정규성 검정
|    ├── kstest               # Kolmogorow-Smirnov 검정(분포 적합성 검정)
|    ├── probplot             # Q-Q Plot 생성(정규성 시각화)
|    ├── pearsonr             # 피어슨 상관계수 계산
|    ├── spearmanr            # Spearman 순위 상관계수 계산
|    └── describe             # 기술 통계량 제공(평균, 표준 편차등)

Z-검정

• 양측검정

  • 귀무가설 : 모집단 평균($\mu$)이 특정 값($\mu_0)$과 같을 것
  • 대립가설 : 모집단 평균($\mu$)이 특정 값($\mu_0)$과 같지 않을 것

• 단측 검정

  • 귀무가설 : 모집단 평균($\mu$)이 특정 값($\mu_0)$보다 클 것
  • 대립가설 : 모집단 평균($\mu$)이 특정 값($\mu_0)$보다 작을 것

• 통계량

  • Z-score
    • $Z = \frac{\bar{x} - \mu}{\sigma / \sqrt{n}}$

t검정: 두 그룹 평균 비교

• 귀무가설 : 두 집단의 평균이 같다

• 대립가설 : 두 집단의 평균이 다르다

  • 두 그룹 등분산성, 정규성에 따라 방법 다름

• AB test의 경우, 랜덤 배정되기 때문에 등분산성 만족

• N ≥ 30 -> 일반적으로 정규성 만족

• 독립 이표본 t-test 대부분 적용

  • 일반 관찰 연구의 경우: scipy.ttest_ind 함수 전달인자 변경 혹은 적용 함수 변경

데이터 정규성, 등분산 검정

• 정규분포 만족

  • H0 : 데이터는 정규 분포 따름
  • H1 : 데이터는 정규 분포를 따르지 않음
  • Shapiro-Wilk
    • 특징 : 작은 표본(n≤50)에 적합
  • Kolmogorov-Smirnov
    • 특징 : 표본이 클 때 적합

• 등분산 만족

  • H0 : 각 그룹 분산은 동일
  • H1 : 적어도 한 그룹의 분산이 다름
  • Levene
    • 여러 그룹 분산의 동일 검정
    • 정규성 검정 필요 하지 않음
  • Bartlett
    • 데이터가 정규 분포를 따른다는 가정
    • 정규성 만족 시 Levene보다 검정력 높음!

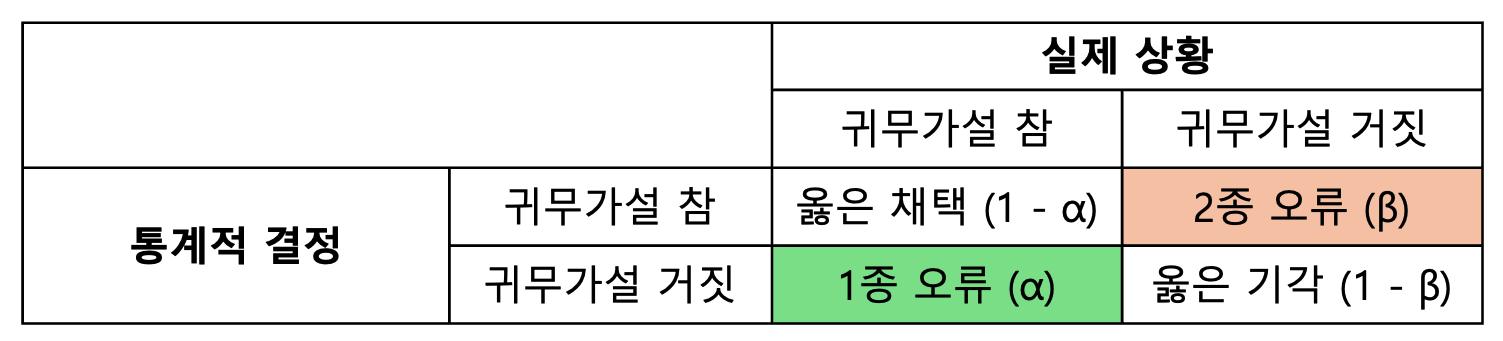
1종 오류

• 귀무가설은 본래 믿고 있는 사상 또는 주제
• 대립가설은 새로운 주장
• 귀무가설이 참임에도 -> 귀무가설 채택을 하지 않는 오류인 1종 오류 관리

2종 오류

• 실제 효능이 있음에도 효능이 없다고 판단하는 오류
• 국민 위해성에는 관련이 있지 않아 덜 엄격하게 관리
• 1종 오류 및 2종 오류의 트레이드 오프 -> 둘 다 낮은 수준으로 관리는 안됨

검정력

• 특정 표본 조건(크기 및 변이) -> 효과 크기(이펙트)를 알아낼 수 있는 확률
• 오류 관점 : 대립가설이 참일 경우 올바르게 기각할 확률 <-> 1종 오류(유의 수준)
• 통상 산업 표준 : 80%

• 몇 개의 데이터를 수집해야하는지 -> 3가지 인자에 영향
  • 탐지하고자 하는 효과 크기
  • 유의 수준 : 0.05(산업계 표준)
  • 검정력 : 80%(산업계 표준)
• 탐지하고자 하는 효과 크기 결정하면 됨
  • $n = (\frac{z_α + z_β}{d})^2$
    • $z_α$ : α에 대응하는 정규분포 z값
    • $z_β$ : β에 대응하는 정규분포 z값
• 단측 검정
  • 필요한 각 그룹 데이터 개수(n)
  • $n = (\frac{1.96 + 0.84}{d})^2$

실습 코드 : Day3 추론통계심화(A/B test)_이하얀